黑土区水稻耗需水过程与产量形成及水分利用的响应关系

魏永霞，汝 晨，刘 慧，杨军明，侯景翔，张 奕

(1.东北农业大学水利与土木工程学院，哈尔滨 150030；2.农业部农业水资源高效利用重点实验室，哈尔滨 150030；3.东北农业大学理学院，哈尔滨 150030)

黑龙江省作为我国商品粮主要输出地，水稻种植面积逐年增加，灌溉用水供应日趋紧张。研究不同生育阶段水分调控对水稻产量影响，为提高水稻水分利用效率提供理论依据，对保证我国粮食产能及农业可持续发展具有重要意义。

水分调控可减少株间蒸发、渗漏损失、土壤蒸腾等因素引起的水分流失，提高产量及水分利用效率[1]。学者分别从不同生育期、不同程度干旱等角度探究水稻产量及水分利用。彭世彰等研究表明，抽穗开花期对水分亏缺响应敏感，充足水分有助于开花授粉，水分不足结实率降低，产量大幅度下降[2]。迟道才等认为分蘖期、拔节期+抽穗期耗需水对产量影响较大，分蘖期和乳熟期中度亏水互作效应可显著提高水分生产效率[3]。杨生龙等在淹水和节水栽培两种土壤水分条件下研究发现，水稻每亩有效穗数、穗粒数差别较小，而极度节水栽培下水稻有效穗数、穗粒数极低，导致产量严重下降[4]。汤洪等认为结实中期轻度水分胁迫有利于提高籽粒灌浆速率，重度亏水则结实率降低，影响产量[5]。董淑喜等研究发现，生育中期连续中旱对产量影响较大；灌浆乳熟期适当建立无水层，有利于产量及水利用效率提高[6]。目前，水分胁迫对水稻产量形成研究较多，但主要集中在单一阶段、同等水分胁迫程度下对作物产量形成及水分利用影响，缺乏科学系统比较分析；针对产量形成及水分利用效率对耗水过程响应分析研究较少，缺乏耗水过程对产量形成及水分利用响应关系研究。

水分生产函数可定量评估季节性水分利用与水稻产量关系，估测最优灌溉深度，为作物调亏灌溉和补充灌溉提供理论依据[7]。目前，国外水分生产函数模型围绕小麦、玉米、棉花、洋葱等作物开展研究[8-11]，包括作物腾发量与作物产量关系，盐分、水肥胁迫下作物生产函数，围绕作物产量与阶段耗水量研究，寻求最优灌溉制度，利用水分生产函数建立生产总净效益模型等。国内学者作物水分生产函数研究主要集中在水稻、小麦、玉米等作物[12-16]。一部分围绕旱作夏玉米、冬小麦等作物，如水分生产函数模型筛选验证[15]，围绕Jensen模型开展参数计算，高斯-牛顿法求解Jensen模型参数[17]，采用生长曲线描述作物Jensen模型下水分敏感累积函数[18]；另一部分关于水稻水分生产函数研究，包括适用各地水稻水分生产函数模型，模型求解方法，模型空间移用等内容。付红等优选适合查哈阳灌区水稻水分生产函数模型[19]，沈细中等建立水稻水肥动态生产函数-修正Mogran模型[20]；迟道才等研究水稻动态水分生产函数[13]；崔远来等研究水稻水分敏感指标空间变异规律及等直线图[21]。但寒地黑土区水稻水分生产函数对比研究较少。

本试验研究各时期耗水量对产量及水分利用效率影响效应、明晰产量及其构成要素对耗水过程响应关系，旨在探索不同阶段控水效应及缓解措施，寻求最优水分生产函数模型，为寒地水稻制定高产、稳产灌溉制度提供技术支撑和理论基础。

1 材料和方法

1.1 研究区概况

试验于2017年5～9月在黑龙江省庆安县和平灌区水稻灌溉试验站开展，北纬46°41'至47°4'，东经127°20'～127°49'，属于北温带半干旱、半湿润大陆性气候。多年平均降水量550 mm，多年平均温度2.5℃，全年无霜期128 d。试区土壤种类为白浆型水稻土，容重为1.02 g·cm-3，孔隙度61.6%，0～30 cm体积饱和含水率平均为55.5%。土壤耕层颗粒分级：砂粒（＞0.02 mm）、粉粒（0.002～0.02 mm）、粘粒（＜0.002 mm）质量分数分别为24.4%、38.7%、36.9%。土壤基础理化指标：pH为6.51，有机质41.5 g·kg-1，全氮 15.10 g·kg-1，全磷15.21 g·kg-1，全钾20.09 g·kg-1，碱解氮 153.98 mg·kg-1，有效磷25.21 mg·kg-1与速效钾157.19 mg·kg-1。

1.2 试验设计

使用规格相同，面积为1 m2蒸渗仪，土壤制备填装过程按照原状土密度、含水量等指标，将配制土体人工分层回填入四周和底部封闭的特制排水、供水系统蒸渗仪内，底部垫以一定厚度砂质反滤层，蒸渗仪内所盛土样表面与场内地面齐平，土体深度1 m，测试精度0.1 mm。供试水稻品种为龙庆稻3号，插秧规格为行株距22.5 cm×12.5 cm，4行24穴，每穴5株，配备移动式遮雨棚，防止干扰。蒸渗仪外侧种植同一品种水稻作为保护田。由于插秧至分蘖前期不需灌水，黄熟期稻田水分自然落干，依据作物各生育阶段长度接近等原则，以水稻6个生育阶段耗水量为试验因素，采用U7（76）均匀试验设计，在适宜灌溉水层上限与重度调亏之间设置6个水分调亏水平，对照水分按正常灌溉适宜水分条件管理，7个处理，3次重复，共21个蒸渗仪。水稻不同生育阶段水分调控标准及生育期时间划分（见表1）。

由表1可知，所有试验小区均田间管理方法相同，施肥，除草等均保持一致，全生育期总施氮为110 kg·hm-2，基肥∶分蘖肥∶促花肥∶保花肥=4∶2∶1.5∶2；施P2O5为45 kg·hm-2，全部用于基肥一次性施入；施K2O为80 kg·hm-2，分基肥和水稻8.5叶龄时期（幼穗分化期）两次施入，比例为1∶1。施肥时间：基肥（5月15日）、分蘖肥（6月10日）、促花肥（7月17日）、保花肥（7月24日）。供试作物品种为龙庆稻3号，于2017年5月19日插秧，9月20日收获。

表1 水稻不同生育阶段水分控制标准Table 1 Water control standards at different growth stages of rice

1.3 观测指标与方法

1.3.1 作物耗水量

分蘖前期水分调控，于每日8:00使用称重式蒸渗仪获取累积1 d蒸散量。当水分调控下限为水层或土壤含水率时，分别用专用水尺或便携式土壤水分速测仪测量，当受旱处理土壤含水量达控制下限时开始灌溉至设计上限，灌水量由安装在供水管道上水表确定。试验在自动感应式遮雨棚内，蒸渗仪底部排水，故不考虑生长季内降雨量、地表径流量、地下水补给量影响。因此，作物耗水量计算公式为：

式中：ETc为阶段耗水量（mm）；ΔW为计算时段储水量差值（mm）；I为计算时段内灌水量（mm）。

1.3.2 考种与测产

成熟期每个蒸渗仪选取10穴代表性水稻计产，取3穴水稻用于考种，单打单收计算每穴实际产量，根据每公顷穴数计算单位面积产量。测定水稻产量构成要素：单位面积有效穗数、穗粒数、结实率、千粒重。

1.3.3 水分利用效率

计算公式为：

式中：WUE为水分利用效率（kg·m-3）；Y为单位面积水稻产量（kg·hm-2）；ET为全生育期总耗水量（m3·hm-2）。

1.4 水分生产函数

水分生产函数反映作物生产过程中产量与耗水量之间关系，是限水灌溉和有限水资源优化调配基础。目前国内外常用模型主要有加法和乘法模型，从宏观角度反映作物产量与各时期蒸散量关系，本研究选择国际上通用Jensen、Blank、Stewart和Singh用于地区性验证，确定当地最佳水稻水分生产函数模型。4个模型[22]表达式如下：

式中：Ya为各处理实测产量；Ym为充分灌溉处理产量；ETa为各处理实际蒸散量；ETm为充分灌溉处理蒸散量；n为生育期数，n=6；i为生育期编号；λi为各生育期水分敏感指数；Ai、Bi、Ci为各生育期水分敏感系数。

1.5 数据分析

采用Excel 2010数据处理与绘图，SPSS 22.0作数据相关分析，采用最小显著性差异法（LSD）作多重比较，显著水平为P＜0.05。运用偏差（AE）、均方根误差（RMSE）、变异系数（Cv）、模拟能力指数（EF）、残差聚集系数（CRM）分别分析Jensen和Stewart模型模拟精度，公式参见文献[23]。

2 结果与分析

2.1 各生育阶段耗水量对产量及其构成要素影响效应分析

2.1.1 耗水量对水稻产量影响效应分析

采用U7（76）均匀试验设计，以不同生育期耗水量为自变量因素，共6个因素，分别为分蘖前期耗水量(x1)、分蘖中期耗水量(x2)、分蘖后期耗水量(x3)、拔节期耗水量(x4)、抽穗期耗水量(x5)、乳熟期耗水量(x6)。不同处理水稻总产量如图1所示，对各时期耗水量与产量多元回归拟合，逐步剔除与因变量不显著因素，得到自变量与水稻产量(y)多元线性回归模型为：

图1 不同处理水稻总产量Fig.1 Rice total yield of different treatments

对式（7）显著性检验，P＜0.01，回归关系达极显著水平，决定系数R2=0.830，表明预测产量和实际产量拟合良好。各因素t检验及显著性检验结果见表2。由表2可知，模型中各因素关于产量(y)回归分析具有统计学意义，由于各因素量纲相同，回归系数绝对值可判断各因素对因变量影响程度。由式（7）可知，因素x2、x4、x5、x6对产量具有显著影响，影响效应为正；x1、x3对产量影响不显著。各时期耗水量对产量影响顺序为：x5＞x4＞x2＞x6。

表2 产量模型回归系数检验Table2 Test of regression coefficient of yield model

分蘖前期水稻各器官尚未发育成熟，光合同化潜能和生理活动均处于较弱水平，x1对产量影响未达显著水平。x2回归系数为31.587，此阶段茎蘖增长速度加快，地上部群体冠层覆盖率与光合物质积累速率迅速提升，水量需求较高，亏水导致有效穗数减少，影响最终产量。x3与产量未达显著水平，原因是此阶段茎蘖数量基本达到高峰，主要控制无效分蘖发生，对水分要求较低。x4回归系数较高为34.587，拔节期正值水稻由营养生长转到生殖生长关键时期，也是水稻全生育期需水临界期，拔节期水分不足造成枝梗及颖花发育不健全，颖花畸形不能正常开花结果，严重缺水则使花粉与卵细胞发育受阻，孕穗过程难以继续而严重减产。此时期保持一定水层除直接满足水稻生理需水外，还能使土壤中铵态氮保持稳定，肥效不易脱失，为植株生长孕穗创造良好营养条件，利于产量提升[24]。x5回归系数最高为35.297，因为抽穗期缺水减弱光合作用，降低植株体内碳水化合物，影响籽粒形成，严重亏水则使水稻出穗困难；此时期充分灌溉可满足植株吸水吸肥需求，调节水温、地温，促使水稻穗部发育提早多穗大穗，提升产量。x5系数高于x4，由于拔节期水量充足促进水稻幼穗分化进程，对水稻后期籽粒灌浆及形成起关键作用，故x4系数较高。但由于抽穗期是水稻光合作用及新陈代谢最旺盛时期，也是水稻对水分反应最敏感阶段，此时正值整个生育阶段温度最高时期，为满足水稻生长、生理所需水分，防止高温影响作物生长，可适当加深灌溉水层，减少水稻过度蒸腾影响穗部生殖器官发育[25]，因此x5对产量影响最大。x6回归系数最低为20.658，此时作物籽粒基本形成，耗水量大幅降低，可适当降低控制下限以利水稻收割。

2.1.2 耗水量对产量构成要素影响效应分析

不同处理下水稻产量构成要素如表3所示。分别对有效穗数(y1)、穗粒数(y2)、结实率(y3)、千粒重(y4)与各时期耗水量多元线性逐步回归分析，剔除与因变量不显著因素，得到回归方程分别为：

方程(8)～(11)均在P＜0.01下达极显著，且决定系数R2＞0.80，说明拟合效果良好，可较好反映水稻产量构成要素与不同阶段耗水量间关系。

由表4可知，各因素均满足模型参数验证。各时期耗水量对有效穗数影响顺序为：x5＞x4＞x6＞x2＞x3，各因素影响效应均为正。x2比x3系数大，表明分蘖中期耗水量比分蘖后期对有效穗数影响更大，原因是分蘖中期茎蘖生长旺盛，供水充足显著增加有效分蘖；拔节期和抽穗期属于孕穗出穗重要阶段，耗水量对有效穗数影响效应显著大于其他时期。各时期耗水量对穗粒数影响顺序为：x5＞x4＞x6＞x1，x6对产量影响效应为负。对于穗粒数来说，x4、x5系数分别为0.184、0.343，水稻在拔节、抽穗需水关键期要保证作物颖花形成与消退阶段供水充足，使颖花生长发育良好，穗粒数增多。结实率是影响产量关键因素，各时期耗水量对结实率影响顺序为：x4＞x5＞x6＞x3，其中x3、x4、x5影响效应为正，x6为负效应。x6系数为-0.037，原因是乳熟期适度水分胁迫利于改善穗粒中淀粉合成和籽粒灌浆速率，帮助增加籽粒饱满充实度，尤其是在水稻生长关键期，其回归系数分别为0.120、0.102，应首先满足此阶段供水，反之花器发育不良，水稻结实率降低。各时期耗水量对千粒重影响顺序为：x5＞x4＞x6＞x3，x3对千粒重影响效应为负。由于分蘖后期适当亏水可促进水稻根系吸水能力和光合物质生产，帮助籽粒成熟提高粒重。x5对千粒重影响效应最大，x4次之；虽然乳熟期籽粒灌浆作用显著决定千粒重，但以关键生育期花器良好发育为前提，关键期亏水，对后期穗部性状造成影响，故 x4、x5系数大于 x6。

计算各产量构成要素指标与相关系数结果见表3。产量构成要素与产量均呈显著或极显著正相关，分析产量构成要素对耗水过程响应关系可明确产量对耗水过程影响机制。分蘖中期供水充足促进水稻分蘖旺盛，低位分蘖多，易形成合理高产群体，分蘖后期耗水量对千粒重产生负向影响，原因是适当亏水可维持水稻根系活动，促进光合速率和籽粒成熟，粒重提高而增产。同时，产量构成要素均对关键生育期耗需水过程响应较为敏感，足够水量使穗部生殖器官获到良好发育，同时利于累积同化物质由茎叶向谷粒输送，提高水稻穗粒中淀粉合成速度，有助于群体穗数、穗粒数增多，结实率、千粒重提高，为高产水稻提供基础[26]。乳熟期适当水分胁迫可改善土体空气流通性，增强作物对土壤有机物质吸收利用，改善籽粒灌浆速率，提高穗粒数和结实率，显著提升产量。

表3 不同处理产量构成要素及与产量相关系数Table3 Rice yield and yield components of different treatments

表4 产量构成要素回归系数检验Table4 Test of regression coefficient of rice yield components model

2.2 各生育阶段耗水量对水分利用效率影响效应分析

水分利用效率是表示作物水分吸收利用过程效率重要指标。不同处理水分利用效率如图2所示。

图2 不同处理水稻水分利用效率Fig.2 Rice water use efficiency of different treatments

利用各时期耗水量与不同处理WUE多元线性回归拟合，得到模型如下：

式（12）在P＜0.01下达极显著，回归关系达到极显著水平，其决定系数R2=0.821，表明模型拟合效果较为理想，回归系数检验结果见表5。从回归系数可知，各时期耗水量对WUE影响顺序为：x5＞x4＞x1＞x3＞x6，因素x1、x4、x5、x6对水稻WUE均具有显著正向影响，x3为显著负向影响。由于根部在分蘖前期尚未完全恢复对水分利用能力，田间保持温湿环境可增强根系对水分吸收作用，满足群体生态需水，为植株营养器官创造适宜发育环境，此时期生理需水较低，营养器官发育良好为前提，利于最终产量形成，提高WUE。x2与WUE未达显著水平，因为水稻分蘖旺盛引起耗水量增加，对水稻产量提升产生正向作用，两正向趋势抵消对WUE调控作用，x2对WUE不显著。分蘖后期适当水分调控可促进有效分蘖，保证后期成穗率而增产，因而x3对WUE影响为负。拔节期、抽穗期正值水稻需水临界期，此期水分亏缺易造成稻穗器官发育受阻，极大影响产量而降低WUE。保证水分供应会增强光合物质，促使叶鞘和茎秆光合产物向穗部转运，对后期籽粒良好发育具有决定作用，由耗水量增加引起产量提升幅度高于耗水量本身增加幅度，故x4、x5对WUE为显著正影响。乳熟期水稻逐渐步入生殖生长末期，叶片枯黄凋落且光合作用强度显著下降，对水分吸收利用能力相比关键生长期减弱，x6系数较低为0.003。

表5 水分利用效率模型回归系数检验Table5 Test of regression coefficient of WUE model

2.3 水稻水分生产函数

2.3.1 水分生产函数优选

构建水分生产函数模型关键是确定适合当地生产实际的具体参数。分别计算Jensen、Blank、Stewart和Singh模型水分敏感指数，确定和平灌区最佳水稻水分生产函数，结果见表6。

表6 4种水分生产函数模型敏感指数及拟合优度Table6 Sensitivity index and coefficient of four water production function models

由表6可知，4个水分生产函数模型R2均在0.98以上，拟合效果较为理想。对于Jensen模型，λi值越高，因缺水导致减产幅度越大，其水分敏感指数顺序为抽穗＞拔节＞分蘖中期＞乳熟期＞分蘖前期＞分蘖后期，与水稻实际生长特性吻合，模型拟合优度R2为0.984，故Jensen模型可作为和平灌区寒地水稻水分生产函数；Blank模型表明，Ai值越大，因水分亏缺造成减产程度越轻，该模型水分敏感指数在抽穗期达到最大值，证明该阶段水分亏缺对产量影响最小，与水稻生理活动和田间管理经验矛盾。由于Blank模型为加法模型，不能反映前一阶段缺水对后一阶段影响，事实上，在水稻生长过程中前阶段亏水对后期生长造成累积影响[27]。因此，Blank模型不适合作为和平灌区水稻水分生产函数模型；Stewart模型Bi值与Jensen模型λi值含义相同，水分敏感指数在拔节、抽穗期较大，乳熟期最低，拟合优度R2为0.982，拟合效果较好，因此和平稻灌区采用Stewart模型可行。Singh模型表明Ci值越小则亏水时减产越严重，Ci最高值出现在抽穗期，分蘖后期和乳熟期敏感指数出现负值，由于该时期水分调控未达到理想状态，该模型认为各时期亏水对产量影响独立，即使某一阶段水稻受旱绝产仍存在理论产量，与水稻灌溉生产实践不符[28]；从回归结果看Jensen和Stewart模型均可用于描述和平稻灌区水稻产量对耗水过程响应规律。

为确定和平灌区最佳水稻水分生产函数，采用偏差AE、均方根误差RMSE、变异系数Cv、模拟能力指数EF、残差聚集系数CRM分别分析两个模型模拟精度，结果见表7。

表7 模型模拟结果精度分析Table7 Accuracy analysis of simulated results

评价指标AE、RMSE、Cv取值越小表明试验实测值与模型模拟值误差越低，0为最好。CRM可为正值或负值，正值表示对实测值模拟偏高，负值表示对实测值模拟偏低，0表示模拟精度最好。EF取值范围-∞～1，1表明模拟精度最高。总体来看，Jensen模型各统计指标基本优于Stewart模型，因此确定Jensen模型作为黑龙江省和平灌区最佳水稻水分生产函数，其表达式为：

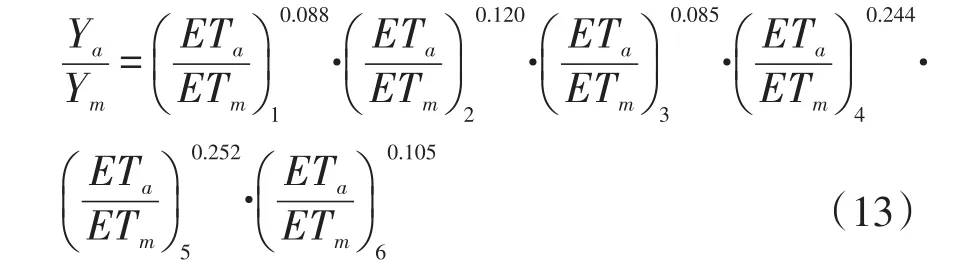
将Jensen模型模拟各处理产量与实测产量对比，二者线性关系较好，结果如图3所示。

2.3.2 Jensen模型水分敏感指数变化过程

不同时期水分敏感指数在全生育期上为连续变化，可以绘制λ在全生育期内变化过程曲线，计算任何时间λ值，如图4所示，图中T为插秧后天数占全生育期天数百分比（%）。

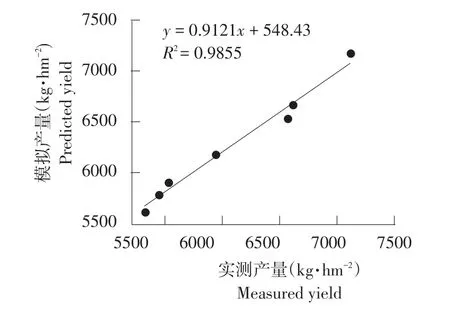
图3 Jensen模型实测产量与模拟产量拟合Fig.3 Measured and predicted yield Fitting

图4 水稻λ值在全生育期变化过程线Fig.4 Change process line ofλin whole growth period

水分敏感指数随插秧后天数变化规律可表示为：

水分敏感指数可反映作物不同生育期缺水减产生物学特性。对于寒地黑土区水稻，分蘖前期λ值处于较低水平，此时功能叶片逐渐形成且以营养生长为主，植株生长缓慢对水分亏缺不敏感；从分蘖前期λ值开始逐渐增大，到分蘖中期达到第一个高峰，此阶段为茎蘖生长旺盛时期，供水充分增加有效分蘖，易形成合理高产群体。分蘖末期λ值全生育期最低为0.085。表明产量对此时期缺水最不敏感，适度缺水促进有效分蘖，提高成穗率。拔节期λ值急剧增大，至抽穗开花期达到最大值为0.252。随气温持续升高，植株生长旺盛且群体冠层覆盖率增大，茎秆及叶片营养物质逐渐转移至穗部籽粒中，拔节、抽穗期是产量形成最关键时期，也是整个生育期需水关键时期。应合理调控灌溉水量，满足水稻发育生长所需水分。开花期过后，水稻逐渐步入生殖生长末期，叶片干黄枯萎，光合作用及蒸腾速率逐渐减弱，乳熟期λ值为0.105。综上，灌溉水量有限时应优先分配给分蘖中、拔节、抽穗需水关键期，而分蘖前期、分蘖后期、乳熟期为非需水关键期，土壤湿润即可满足作物正常生长发育，获得高产同时最大程度节水，实现高产高效目标。

3 讨论

水分亏缺存在于水稻任何生长发育阶段，具有不同响应和耐旱机制。在营养期和早期生殖期发生非充分灌溉，水稻产量下降与千粒重和穗粒数密切相关，与当阶段施加非充分灌溉时间呈正比[29]。拔节孕穗期和抽穗开花期是对水分胁迫最敏感阶段，自花授粉水稻在此阶段遭受水分胁迫可造成小花退化或花粉不育而严重减产[30]。从产量回归模型可知，分蘖中期与拔节期耗水量对产量回归系数分别为31.587、34.784，差异不明显；抽穗期回归系数最大为35.297，表明其对产量响应关系最为强烈，乳熟期回归系数最低为20.658。与Belder研究结果一致[31]。产量构成要素与产量具有显著正相关，分蘖中期水分亏缺影响分蘖成穗；水分最敏感时期是生殖细胞形成期，水分胁迫使颖花退化、降低穗粒数和千粒重，不利于产量提高。结实中期轻度水分胁迫有利于改善籽粒灌浆速率，但后期水分不足，水稻结实率降低，影响产能发挥[5]。本研究中拔节、抽穗期耗水量均对产量构成要素影响显著，分蘖后期和乳熟期耗水量对有效穗数和千粒重调控效果较低，而穗粒数和结实率均表现乳熟期适当亏水有利于指标及产量提高。另外，水分胁迫引起谷粒接受碳水化合物能力下降是导致结实率降低主因，拔节孕穗期和抽穗期水分胁迫造成的结实率降低最严重，王成瑷等研究结果表明，分蘖期发生水分亏缺，虽然单株穗粒数增加，但有效穗数显著下降[32]。差异可能由作物种类、土壤环境因素及水分调控上下限差异导致，有待深入研究。

不同时期耗水量对水稻WUE影响效应存在一定差异。本研究结果表明，拔节期和抽穗期耗水量对WUE正向效应最大，由于拔节、抽穗期水分充足促进花粉与卵细胞发育，有助于开花授粉，形成大穗、粒多籽粒饱满水稻，此时期耗水量显著提高植株对水分利用程度。而分蘖后期耗水量对WUE负向作用最大，尽管此时期对水量有要求，但水分过多抑制根系与外界气体交换。此时控水可降低无益消耗，促进分蘖，对作物生育后期形成超补偿效应，节水提高WUE[33]。Blum等研究发现早期营养生长发生轻微水分胁迫与充分灌溉下产量接近，但显著提高WUE[29]。彭世彰等研究认为拔节、抽穗关键期水分亏缺会显著降低产量，不利于WUE提高，与本研究结果一致[2]。

和平灌区水稻水分生产函数以Jensen模型为最佳，模型中水分敏感指数在整个生育期内呈两端低，中间高趋势，与程卫国等观点一致[27,34-36]。但本研究中关键生育阶段水分敏感指数较程卫国[27]研究结果略低，由于本研究按照生育阶段接近等时段原则，将水稻分蘖期细化为分蘖前期、分蘖中期和分蘖后期，生育时段划分越细，水分敏感指数越小[35]。水分敏感指数变化规律与水稻耗水规律吻合，分蘖中期、拔节期、抽穗期是水稻需水关键期，再次证实Jensen连乘模型有效性及试验结果可靠性。

4 结论

a.抽穗期耗水量对产量影响最大，乳熟期耗水量影响最小；就产量构成要素而言，拔节期、抽穗期耗水量对产量构成要素影响均比其他阶段大；乳熟期耗水量对有效穗数影响高于分蘖中、后期；分蘖前期耗水量对穗粒数影响最小，分蘖后期耗水量对结实率影响效应最低，乳熟期耗水量对穗粒数、结实率均存在一定负影响；千粒重对分蘖后期耗水量响应程度最低且为负影响。

b.水稻各时期耗水量对WUE响应关系为：抽穗期＞拔节期、分蘖前期＞分蘖后期、乳熟期；分蘖后期耗水量对WUE产生负影响。

c.Jensen模型可较好反映和平灌区水稻产量与耗水量关系，其水分敏感指数为抽穗期＞拔节期＞分蘖中期＞乳熟期＞分蘖前期＞分蘖后期，绘制Jensen模型水分敏感指数变化过程线，确定分蘖中期、拔节期、抽穗期为水稻需水敏感期。

[1] 程建平,曹凑贵,蔡明历,等.不同灌溉方式对水稻产量和水分生产率的影响[J].农业工程学报,2006,22(12):28-33.

[2] 彭世彰,蔡敏,孔伟丽,等.不同生育阶段水分亏缺对水稻干物质与产量的影响[J].水资源与水工程学报,2012,23(1):10-13.

[3] 迟道才,佟延旭,陈涛涛,等.多生育期不同水分胁迫耦合对水稻产量及水分生产率的影响[J].沈阳农业大学学报,2016,47(1):71-77.

[4] 杨生龙,王兴盛,强爱玲,等.不同灌溉方式对水稻产量及产量构成因子的影响[J].中国稻米,2010,16(1):49-51.

[5] 汤洪,吕浩正,杨通洲,等.影响水稻结实率的因素及预防对策[J].湖南农业科学,2013(8):17-18,21.

[6] 董淑喜,徐淑琴.水分胁迫对寒区水稻生长特性及产量的影响[J].灌溉排水学报,2008,27(6):64-66.

[7] Smilovic M,Gleeson T,Adamowski J.Crop kites:Determining crop-water production functions using crop coefficients and sensitivity indices[J].Advances in Water Resources,2016,97:193-204.

[8] Al-Jamal M S,Sammis T W,Ball S,et al.Computing the crop water production function for onion[J].Agricultural Water Management,2000,46(1):29-41.

[9] Najafi M M H,Alizadeh A,Davari K,et al.Determination of water-salinity production function for two cotton cultivars[J].2012,8(3):672-679.

[10] Dehkordi D K,Kashkuli H A,Naderi A.Estimate of optimum water-yield production function of corn under deficit irrigation and different ratios of superabsorbent in Khouzestan Province of Iran[J].Advances in Environmental Biology,2013,7(9):2279-2282.

[11] Brumbelow K,Georgakakos A.Determining crop-water production functions using yield-irrigation gradient algorithms[J].Agricultural Water Management,2007,87(2):151-161.

[12] 侯琼,王海梅,云文丽.基于Jensen模型的内蒙古河套灌区春玉米水分生产函数研究[J].干旱地区农业研究,2016,34(3):84-89.

[13] 迟道才,王瑄,夏桂敏,等.北方水稻动态水分生产函数研究[J].农业工程学报,2004(3):30-34.

[14] 彭致功,刘钰,许迪,等.基于RS数据和GIS方法的冬小麦水分生产函数估算[J].农业机械学报,2014,45(8):167-171.

[15] 张和喜,迟道才,王永涛,等.黔中地区玉米水分生产函数模型适应性评价[J].水土保持研究,2013,20(3):176-179.

[16] 何进宇,田军仓,马波,等.膜下滴灌旱作水稻水分生产函数研究[J].西北农业学报,2015,24(11):41-48.

[17] 罗玉峰,崔远来,朱秀珍.高斯-牛顿法及其在作物水分生产函数模型参数求解中的应用[J].节水灌溉,2004(1):1-2.

[18] 金建华,王仰仁,孙书洪,等.棉花水分敏感指数累积函数研究[J].节水灌溉,2011(7):4-6.

[19] 付红.查哈阳灌区水稻水分生产函数模型试验研究[J].东北农业大学学报,2008,39(2):159-162.

[20] 沈细中,朱良宗,崔远来,等.作物水、肥动态生产函数—修正Morgan模型[J].灌溉排水学报,2001,20(2):17-20.

[21] 崔远来,茆智,李远华.水稻水分生产函数时空变异规律研究[J].水科学进展,2002,13(4):484-491.

[22] 王立坤,单玉芬,马永胜,等.黑龙江省西部半干旱区向日葵水分生产函数试验研究[J].东北农业大学学报,2009,40(4):33-36.

[23] 郑文生,张桂珍,张忠学,等.黑龙江省西部半干旱区玉米水分生产函数建模与评价[J].东北农业大学学报,2011,42(1):61-65.

[24] 水利部农村水利司.水稻节水灌溉技术[M].北京:中国水利水电出版社,1998.

[25] 谢晓金,李秉柏,李映雪,等.抽穗期高温胁迫对水稻产量构成要素和品质的影响[J].中国农业气象,2010,31(3):411-415.

[26] 王唯逍,刘小军,田永超,等.不同土壤水分处理对水稻光合特性及产量的影响[J].生态学报,2012,32(22):7053-7060.

[27] 程卫国,卢文喜,安永凯.吉林省水稻水分生产函数模型的适应性研究[J].灌溉排水学报,2015,34(2):61-66.

[28] 姚宁.基于CERES-Wheat模型的冬小麦动态水分生产函数研究[D].杨凌:西北农林科技大学,2015.

[29] Blum A.Effective use of water(EUW)and not water-use efficiency(WUE)is the target of crop yield improvement under drought stress[J].Field Crops Research,2009,112(2):119-123.

[30] Pandey R K,Maranville J W,Admou A.Deficit irrigation and nitrogen effects on maize in a Sahelian environment:I.Grain yield and yield components[J].Agricultural Water Management,2000,46(1):15-27.

[31] Belder P,Bouman B A M,Cabangon R,et al.Effect of watersaving irrigation on rice yield and water use in typical lowland conditions in asia[J].Agricultural Water Management,2004,65(3):193-210.

[32] 王成瑷,王伯伦,张文香,等.干旱胁迫时期对水稻产量及产量性状的影响[J].中国农学通报,2008(2):160-166.

[33] 沈维,姚帮松,程峰,等.水稻分蘖期生理耗水量研究[J].安徽农业科学,2016,44(22):13-14+39.

[34] 柴江颖,崔远来,汪文超,等.鄱阳湖流域水稻水分生产函数模型试验研究[J].中国农村水利水电,2014(8):1-4.

[35] 韩松俊,刘群昌,王少丽,等.作物水分敏感指数累积函数的改进及其验证[J].农业工程学报,2010,26(6):83-88.

[36] 陈晓楠,黄强,邱林,等.基于遗传程序设计的作物水分生产函数研究[J].农业工程学报,2006,22(3):6-9.