基于复合粒子群自适应液压伺服系统力跟踪控制与试验

2018-01-25苏文海闫聪杰朱光强袁立鹏息晓琳何景峰

东北农业大学学报 2018年1期

苏文海，李冰，闫聪杰，朱光强，袁立鹏，息晓琳，何景峰

（1.东北农业大学工程学院，哈尔滨 150030；2.哈尔滨工业大学机电工程学院，哈尔滨 150001；3.哈尔滨博实自动化股份有限公司，哈尔滨 150078）

随着新型农业移动平台发展，农业足式移动平台对复杂环境适应性及运动灵活性等方面较其他移动方式优势明显，智能控制等高新技术应用成为农业机械装备研究重要方向[1-2]。其中，液压伺服系统作为农业足式移动平台主要传动方式[3]，由于末端位置缺少力跟踪或力跟踪不准确，机器人在田间、山地等复杂路面温室行走时环境刚度及末端位置期望力不断变化，引起机身不稳定，影响作业性能。因此，研究液压伺服末端位置力跟踪控制对促进农业工程技术发展具有重要作用[4-5]。目前，液压伺服系统力跟踪控制主要基于位置阻抗控制策略[6-7]，末端位置力跟踪稳态误差较高，具有系统非线性及参数时变性特点，Sharifi等提出一种自适应阻抗控制策略，可辨识环境刚度及环境位置，补偿期望位置，有效降低末端位置力跟踪稳态误差[8-9]；李二超和刘智光等提出一种基于模糊自适应阻抗控制策略，采用模糊算法通过力偏差及其变化率选择阻尼参数，快速跟踪末端位置期望力[10-11]。

本文提出一种基于复合粒子群自适应控制策略。在建立液压伺服系统数学模型和阻抗模型基础上，根据环境刚度及力偏差采用模糊算法确定阻抗参数范围，结合莱维飞行粒子群对阻抗参数快速通过局部和全局搜索确定阻抗参数，采用3次样条插值拟合阻抗参数随环境刚度变化方程；分析末端位置力跟踪稳态误差原因并建立数学模型，根据末端位置力和当前位置，利用自适应算法估计环境刚度与环境位置对期望位置补偿并选择阻抗参数，运用二连杆串联机构台架试验验证液压伺服系统力跟踪性能。

1 数学模型建立

1.1 液压伺服系统数学模型

液压伺服系统末端位置不与环境发生接触时为纯位置内环控制，参照李冰等方法[12]确立液压伺服系统数学模型。

1.1.1 液压伺服系统结构

液压伺服系统如图1所示，主要由液压伺服阀、液压缸、位移传感器和力传感器等部分组成。

图1 液压伺服系统结构Fig.1 Structure diagram of hydraulic servo system

1.1.2 液压伺服阀数学模型

液压伺服阀包括力矩放大器和伺服阀两部分。力矩放大器将控制器输出偏差电压e转化为驱动电流I，在一定频率范围内，力矩放大器可视为比例环节，则力矩放大系数Ka表示为：

伺服阀为具有非线性特性功率放大器，其传递函数用二阶振荡环节近似表示，即

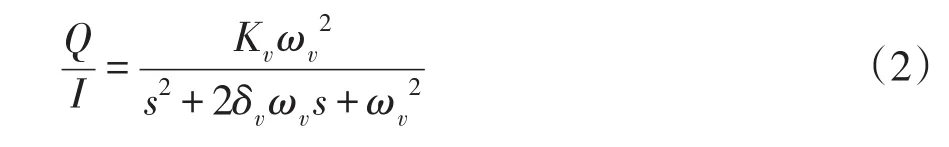
式中，Q-流量；Kv-伺服阀流量增益；ωv-伺服阀固有频率；δv-伺服阀阻尼比。

1.1.3 缸体传动数学模型

缸体传动一般近似等效为积分加上二阶振荡环节，其传递函数为

式中，ωn-液压缸固有频率；δn-动力元件阻尼比。

1.1.4 液压伺服系统

根据式（2）～（3）建立液压伺服系统数学模型结构见图2，各部分参数见表1。

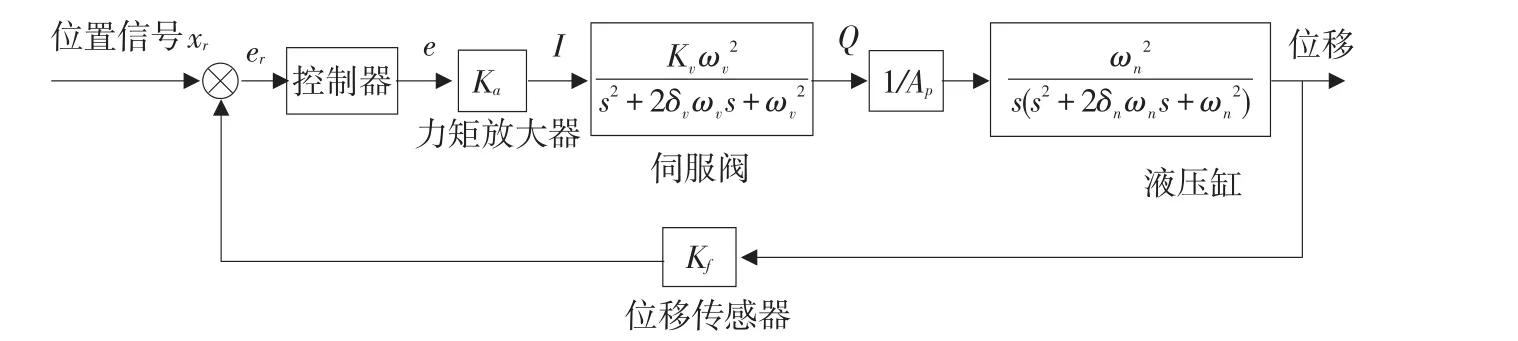
图2 液压伺服系统Fig.2 Hydraulic servo system

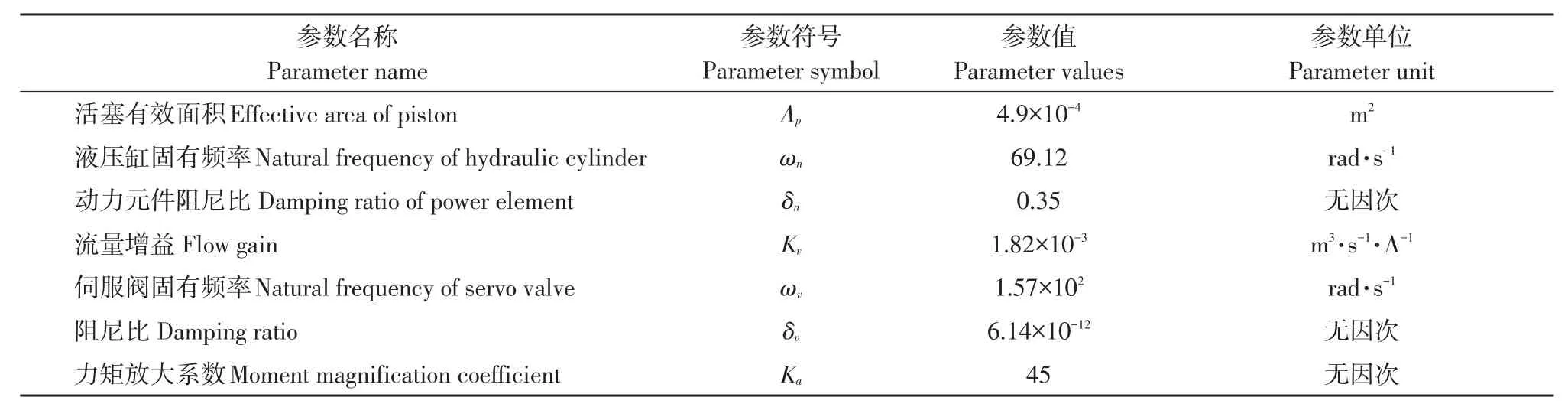
表1 液压伺服系统参数Table1 Parameters of the hydraulic servo system

1.2 阻抗模型建立

1.2.1 基于位置阻抗模型

如图3所示，液压伺服系统末端位置与环境物体发生接触后，液压缸非独立受控对象，而是由液压缸与环境共同组成综合动态系统。环境模型刚度极大，液压缸末端位置受力与其位置偏差用阻抗模型表示为

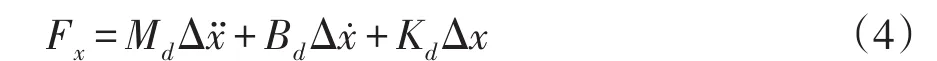
对式（4）拉普拉斯变换可得其传递函数为

式中，Md、Bd和Kd分别表示液压伺服系统期望惯性、期望阻尼和期望刚度；Δx=xr-x表示位置修正量，其中x为当前运动轨迹，xr为期望运动轨迹；Fx表示液压缸末端与环境之间接触力，当液压伺服系统为纯位置控制时为0。

由图3可知，环境模型对液压缸末端位置存在反作用力Fe，其值等于Fx。环境模型根据自身刚度不同会产生位移形变Δxe=x-xe，其中xe为环境位置，环境模型与液压缸末端间相互作用力表示为

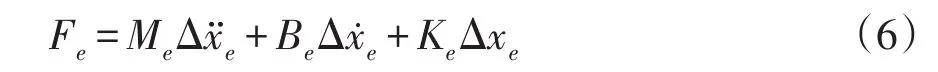
式中，Me、Be和Ke表示环境阻抗参数。

在实际运动中，由于液压缸末端位置运动速度与加速度较小，环境模型与液压缸末端之间相互作用力可简化为

1.2.2 力跟踪模型

由于液压伺服系统在工作过程中，液压缸末端位置需保持一定力，引入期望力Fr构成力闭环，其力学公式为

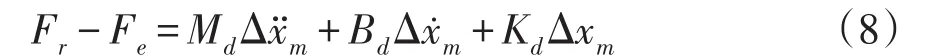
式中，Δxm表示位置偏差，值为x-xr。

基于位置液压伺服系统末端位置力跟踪阻抗控制见图4。

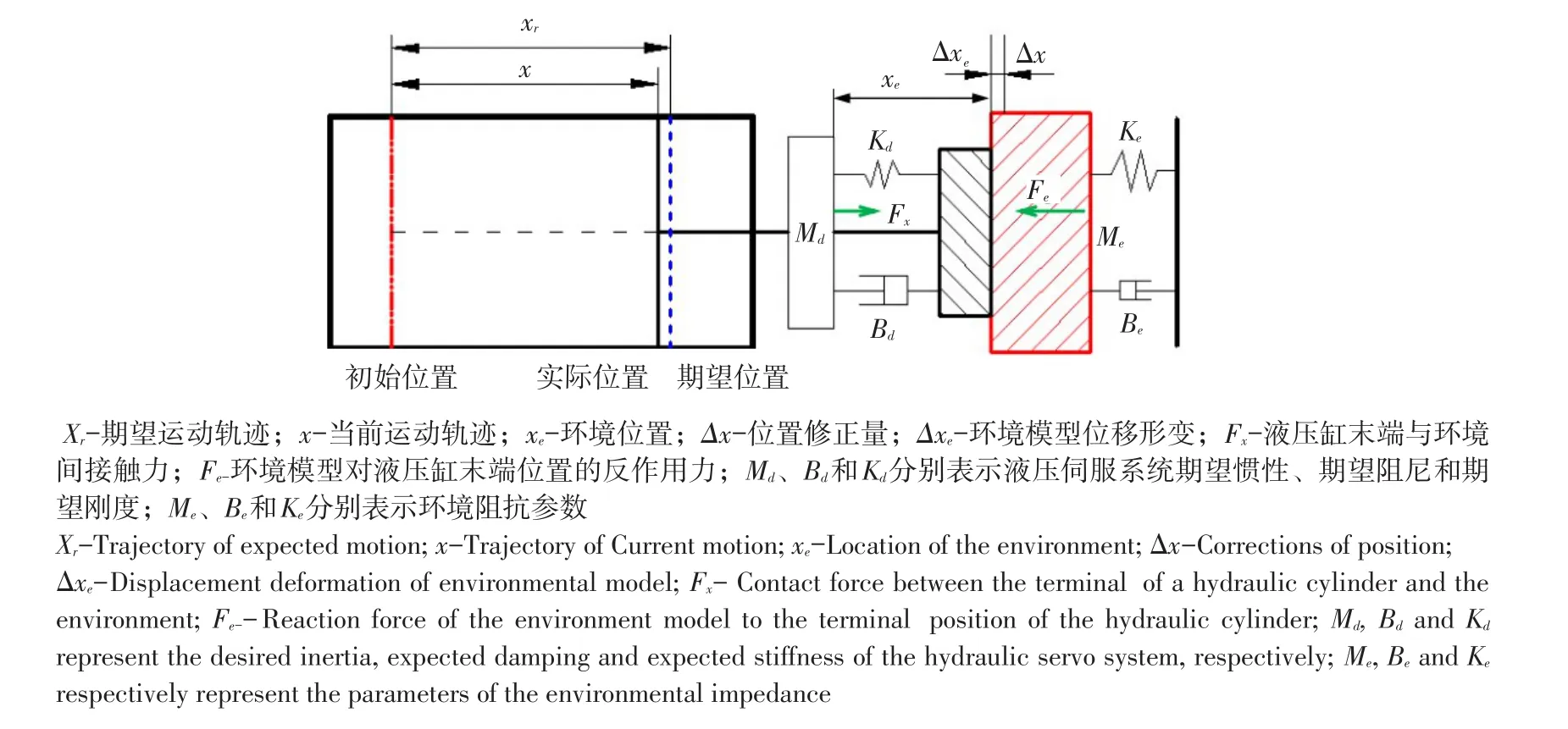
图3 末端位置与接触环境模型Fig.3 Model of the terminal position and the contact environment

图4 位置力跟踪阻抗控制Fig.4 Position force tracking impedance control

2 阻抗控制律设计

期望惯性Md、期望阻尼Bd及期望刚度Kd影响液压伺服系统末端位置修正量[13]。在不同环境模型及期望力条件下，保证液压伺服系统末端位置力快速精确跟踪期望力关键在于控制系统精确寻找阻抗控制参数。针对液压伺服系统力跟踪控制实时性，需通过控制律建立阻抗参数变化方程，使液压伺服系统力跟踪根据末端位置接触环境刚度不同调整阻抗控制参数，提高其末端位置力跟踪控制性能。

2.1 基于复合粒子群阻抗控制律

复合粒子群算法阻抗控制采用模糊算法确定阻抗参数对应种群范围；根据种群范围局部与全局搜索最优解；为防止种群粒子陷入局部最优解，利用莱维飞行策略将进入局部最优解粒子位置重新更新，确定合理阻抗参数。

2.1.1 模糊算法阻抗参数种群范围选择

模糊算法阻抗参数种群范围选择策略是当环境刚度较大时需液压杆伸缩刚度减小，保护系统及环境物体不受变形破坏；当环境刚度较小时需液压杆伸缩刚度增大，满足作业性能。按照力偏差对阻抗参数作相应微调，确定阻抗参数选择范围。

根据环境刚度及其力偏差作为输入，输出为阻抗模型Md、Bd和Kd参数范围。输入与输出各语言变量值集合均为{负大（NB），负中（NM），负小（NS），零（ZO），正小（PS），正中（PM），正大（PB）}，隶属度函数取高斯隶属度函数。输入环境刚度Ke、力跟踪偏差Fe设置论域分别为[0,2000]和[-1000,1000]；输出 Md、Bd、Kd设置论域分别为[0,2]、[0,200]和[0,1000]，则输入与输出FIS关系曲面如图5所示。由图5可知，阻抗参数种群范围可根据不同环境刚度及其力偏差确定阻抗参数搜索范围，保证粒子群搜索精度。

图5 FIS输入输出关系曲面Fig.5 FIS input-output relational surface

2.1.2 速度与位置更新

在粒子群PSO算法中，将阻抗参数看作3组m个粒子组成群体，在1个D=3维空间中搜索，其中第i个粒子表示为1个D维向量Xi=（xi1，xi2，…，xis），每个粒子位置就是1个潜在解。将xi代入目标函数，根据适应值衡量解优劣。

在每次迭代计算中，粒子根据下列公式更新本身速度和位置：

式中：i=1,2,…,m，s=1,2,…,D；C1和C2为非负常数，调节粒子飞向自身及全局最好位置方向步长，一般取2；r1和r2为[0，1]范围内变化且相互独立随机数；ω为惯性权值；n为迭代次数。

为减少进化过程中粒子离开搜索空间，Vis通常限定在一个范围内。

2.1.3 莱维飞行位置更新

由于PSO算法在迭代前期具有较快收敛速度，后期收敛速度慢，易使粒子陷入局部极值[14]。采用莱维飞行进一步判断，对已陷入局部极值粒子作邻域搜索，获得全局最优值。粒子群算法中采用莱维飞行对当前粒子位置Xi更新，更新公式为：

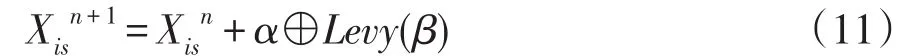
式中，α为步长因子，控制随机搜索范围；⊕表示点乘积；Levy（β）～u=t-1-β表示服从参数为 β莱维分布，β取值区间为1＜β＜3[15]。

根据文献[16]计算莱维随机数，得到莱维飞行更新位置方程为

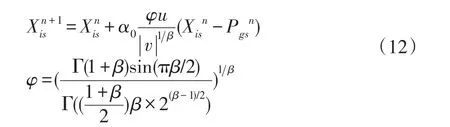
式中，u、v均服从标准正态分布；α0是常数；Γ是标准Gamma函数。

2.1.4 权值改进PSO算法

惯性权值ω是粒子群算法重要参数，调整前一次粒子对当前粒子寻找速度影响。当ω较大时，种群粒子全局搜索能力较强，ω较小时，种群粒子局部搜索能力较强。因此，本文采用基于自适应权重粒子群算法。其权值调整公式为：

式中，ω（t）为粒子群在第t代时惯性权重值；ωmax、ωmin分别代表权重取值区间上限、下限；f为粒子目标函数值，favg，fmin分别表示当前所有粒子平均值和最小值。

该策略中单个粒子通过每次迭代更新选取合适ω值，使种群粒子在全局和局部搜索能力间达到最佳平衡，保证粒子群算法具有较强参数优化能力。

2.1.5 适应度函数

PSO适应度函数作为目标函数对其阻抗参数值优化指标。本文采用绝对值时间积分性能指标作为参数选择最小适应函数，在目标函数中加入控制输入平方项[17]。根据文献[18]选择式（14）作为选取最优指标的适应度函数方程。

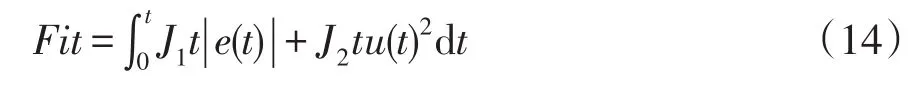
式中，e（t）为Fr-Fe关于时间t变化函数，u（t）为Δx关于时间t变化函数；J1、J2为调节权值。

2.1.6 复合粒子群算法步骤

①根据模糊算法确定种群范围；

②初始化粒子群并设定初始位置和速度；

③计算每个粒子适应值；

④对每个粒子适应值和全局经历最佳位置Pgs适应值比较，若较好，则将其确定为当前全局最佳位置；

⑤对每个粒子适应值和经历最佳位置Pis适应值比较，若较好，则将其为当前最佳位置；

⑥根据式⑩更新权重值；

⑦根据式⑨对粒子速度和位置更新；

⑧如果满足终止条件，则输出解；若不满足终止条件，按莱维飞行更新粒子位置；

⑨按粒子群算法评价适应值；

⑩返回⑧。

2.2 复合粒子群阻抗控制器性能分析

针对液压伺服系统末端位置力跟踪性能分析，分别用常规阻抗控制（见图4）与复合粒子群阻抗控制对比，其中复合粒子群阻抗控制模型采用如图6所示建立测试目标函数，记录液压伺服系统模型在不同环境刚度下跟踪力及当前位置变化情况。

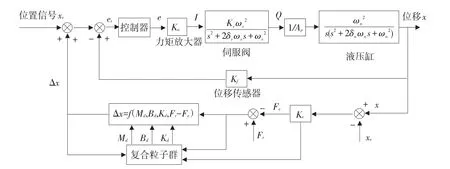
图6 复合粒子群阻抗控制Fig.6 Composite particle swarm optimization impedance control

2.2.1 复合粒子群参数选择

①粒子群参数

惯性因子：ωmax=1.2，ωmin=0.2；加速常数：c1=2，c2=2；种群维数：Dim=3；种群规模：Swarm⁃Size=100；最大迭代次数Iter=100；最小适应值Fit=0.1；适应度函数调节权值J1=0.999，J2=0.01。

②莱维飞行参数

步长因子α0=0.01；莱维参数β=2。

2.2.2 分析测试

利用Matlab-2009b编写程序分析测试，其中输入位置信号为10 mm，干扰末端位置为0.2 mm，期望力为100 N。然后，与复合粒子群搜寻3个输出变量匹配，建立Δx=f（Md,Bd,Kd,Fr-Fe）方程，离散化式（8），采用向前差分方法[19]化为差分格式，得到离散化后阻抗控制器为

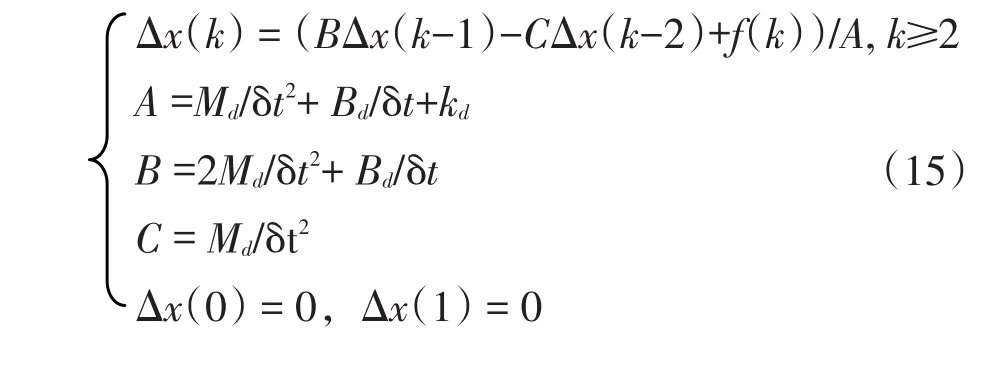
式中：Δx（k）为k时刻位置修正量；f（k）为k时刻沿液压杆方向接触力值（Fr-Fe）；δt为阻抗控制器采样周期。

同时，取不同环境刚度（见表2）（分41组，每组计算10次）分析测试，复合粒子群算法迭代过程中适应度函数值随迭代次数变化趋势如图7所示。

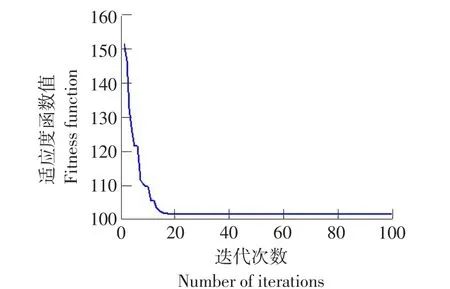
图7 适应度函数曲线Fig.7 Curve of fitness function

由图7可知，每次计算迭代次数均在16～20次时处于完全收敛，其适应值达到最小值后趋于稳定状态。阻抗参数Md、Bd、Kd变化值，液压杆当前位置及跟踪力变化情况如表2所示。

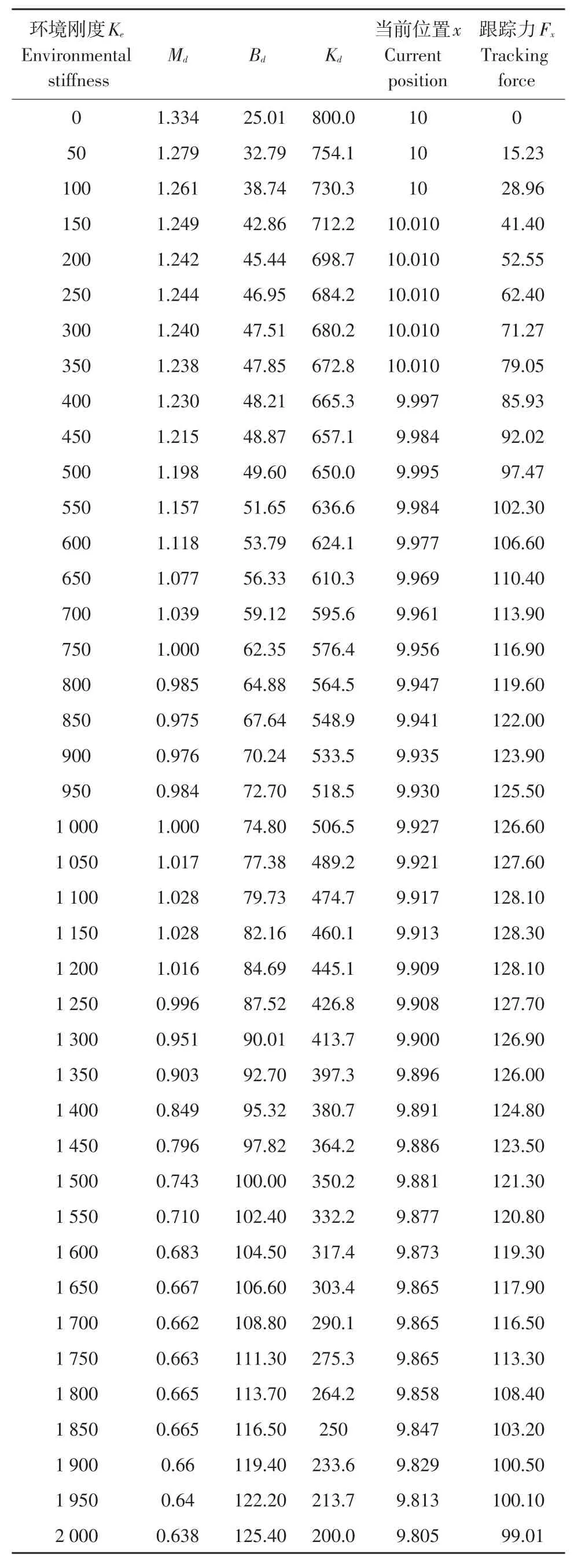
表2 不同环境刚度下测试结果Table2 Test results under different environments tiffness

2.2.3 对比分析

3组不同参数下原始阻抗控制在不同环境刚度测试结果见图8，当前末端位置见图8a，随刚度增大而减小且变化趋势与表2一致，末端位置跟踪力值见图8b，随阻抗参数变化而变化，随环境刚度增大呈线性递增趋势，大于期望力，无法实现良好力跟踪控制性能。

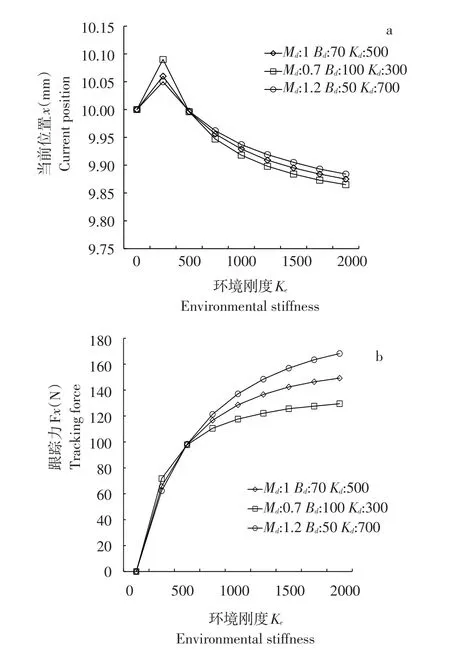
图8 原始阻抗控制分析结果Fig.8 Results of conventional impedance control analysis

与表2对比看出，采用复合粒子群控制阻抗控制器，随环境刚度增大，末端位置接触力变化趋势为先增后减，环境刚度1 000～1 500范围内跟踪力最大，阻抗参数随环境刚度变化自我调整，增强液压伺服系统末端位置力跟踪控制性能。

2.3 阻抗参数变化方程建立

根据表2得到阻抗参数，建立其阻抗控制参数随环境刚度变化连续方程。为保证阻抗参数Md、Bd和Kd随环境刚度变化连续、平滑，采用3次样条插值[20]拟合曲线，如图9所示，图中“*”为表2所示阻抗参数值。

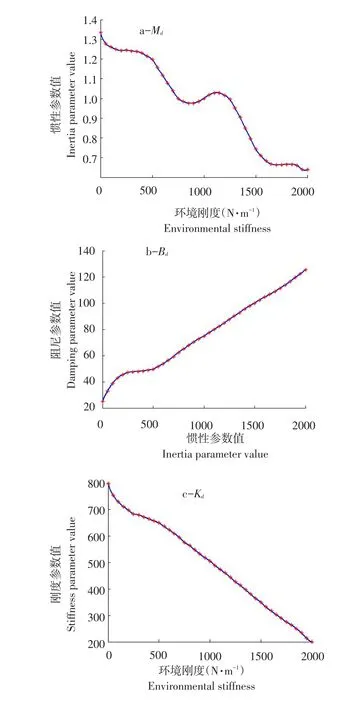
图9 阻抗参数随环境刚度变化拟合曲线Fig.9 Fitting curves of impedance parameters with the change of environmental stiffness

利用Matlab-2009b曲线拟合工具箱cftool拟合所得三次样条插值曲线Sum of Sin Function函数，得到阻抗参数随环境刚度变化3个线性方程，其通项公式为

式中，ai、bi、ci表示方程系数，其中 i∈[1,4]表示方程项数。选择误差平方和趋近于零方程，拟合效果越好，因此阻抗控制参数按照式（16）随环境刚度变化调节。

3 环境刚度估计

通过2.2分析可知，采用复合粒子群阻抗控制律可提高液压伺服系统力跟踪控制性能，但末端位置跟踪力与期望力之间依然存在稳态误差。因此需分析稳态误差产生原因，消除稳态误差，末端位置接触力准确跟踪期望力。

3.1 稳态误差分析

当液压伺服系统末端位置未与环境模型发生接触时，Fe=Fr=0，此时阻抗模型可表示为

当t→∞时，液压伺服系统末端当前位置x可跟踪期望位置xr。当液压伺服系统末端位置与环境模型发生接触时，动态模型按照式（8）运行，即位置偏差Δxm与力偏差Fr-Fe间关系受阻抗模型支配。其阻抗模型为

式中，e为Fr-Fe。

在环境参数一定情况下，为获得恒定接触力，令液压伺服系统末端参考位置xra=xr为定值，则有 ẍra=ẋra=0，则上式表示为

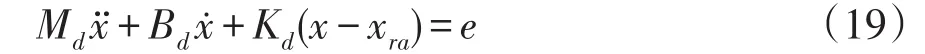
根据式（8）可得到

式中，ke为环境刚度。将式（20）带入式（19）可推出稳态误差数学模型

式（22）可表述为，当液压伺服系统能够获得准确环境位置xe与环境刚度ke，则系统可根据式（22）计算产生液压伺服系统与环境模型期望接触力Fr所需轨迹值xra。

3.2 自适应算法环境参数估计

为使液压伺服系统末端位置与环境接触时可准确跟踪期望力Fr，根据式（22）需要获得准确环境刚度及环境位置，因而采用一种自适应控制算法在线估计环境位置xe与环境刚度ke，这种控制方式

为使液压伺服系统末端接触力在接触环境模型时准确跟踪期望力，即ess→0，需要满足简单，鲁棒性强，可满足液压伺服系统实时性力跟踪控制要求[21]。

根据液压伺服系统末端位置与地面简化接触模型，末端位置接触力为

则末端位置接触力估计值为

令φk=ke-ke， φk=k̂ex̂e-kexe，且 φ =[φk，根据式（23）和式（24），得到力估计误差为

那么，自适应控制器设计目标则变成根据f̂-f 调整环境参数估计值 k̂e和 x̂e，使得当 t→∞时， f̂→ f 。

为保证所设计控制器稳定性，利用Lyapunov第二法及式（25）推导间接自适应算法估计环境位置xe与环境刚度ke估计值为

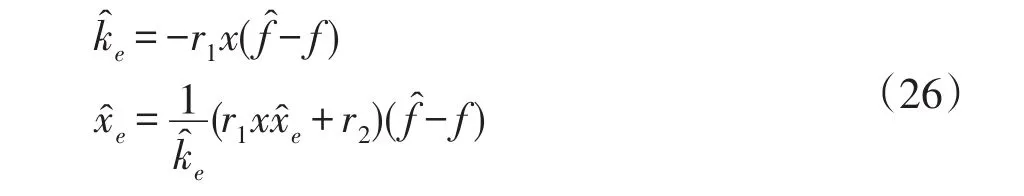
式中：r1、r2为常数，其中r1=0.001、r2=0.003。

3.3 自适应算法复合粒子群阻抗仿真分析

为验证复合粒子群自适应阻抗算法对液压伺服系统力跟踪有效性，分别与原始阻抗和模糊自适应阻抗[11]对比，建立虚拟样机模型仿真测试。

液压伺服系统力跟踪仿真测试采用Adams与Matlab联合仿真模式。采用Solidworks软件建立液压传动系统三维模型并导入Adams中建立机械系统模型。将设置好Adams模型转换成Matlab插件，建立虚拟样机模型。在Matlab/simulink中建立仿真框架，如图10所示。

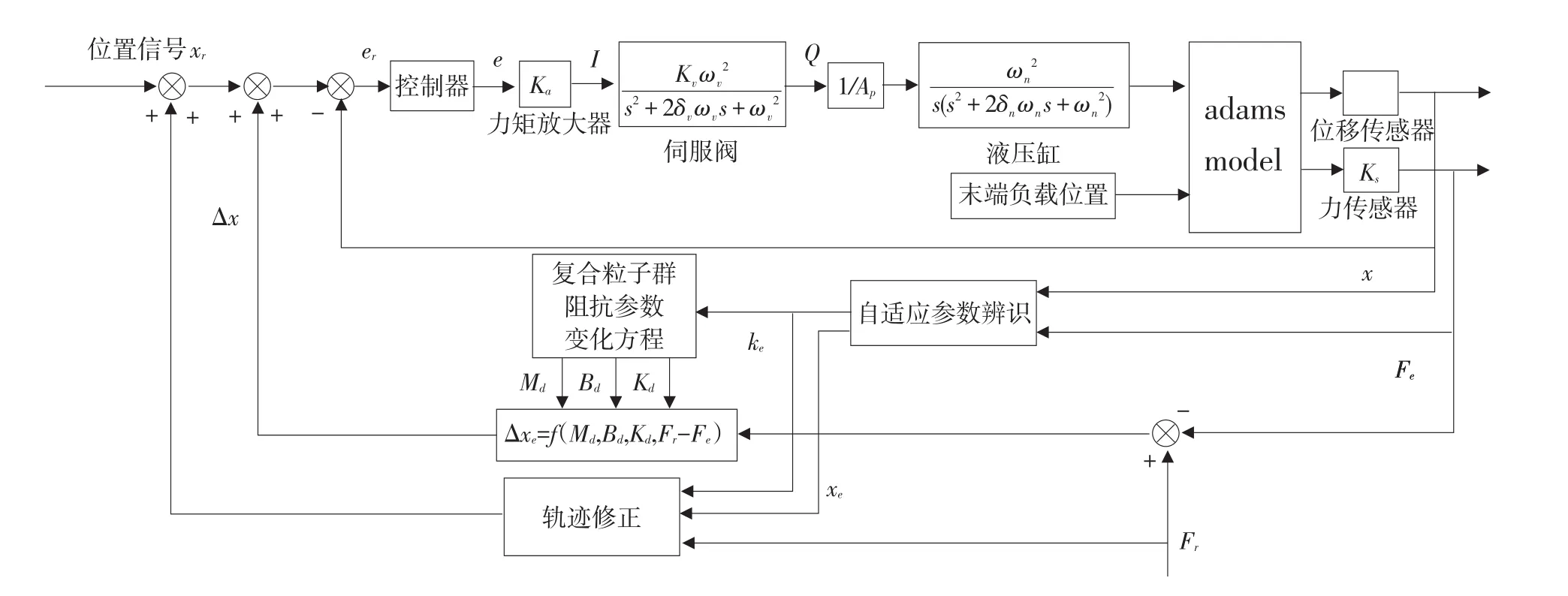
图10 控制系统仿真模型框架Fig.10 Framework of simulation model of control system

如图11所示，在Adams虚拟样机模型中，设置液压系统末端位置，环境模型材料为铝块；在其末端位置添加力、位移传感器；输出位置信号为10 mm，末端位置与环境模型间距离为9.8 mm；仿真步长为10 ms，仿真时间为5 s，并记录仿真结果。

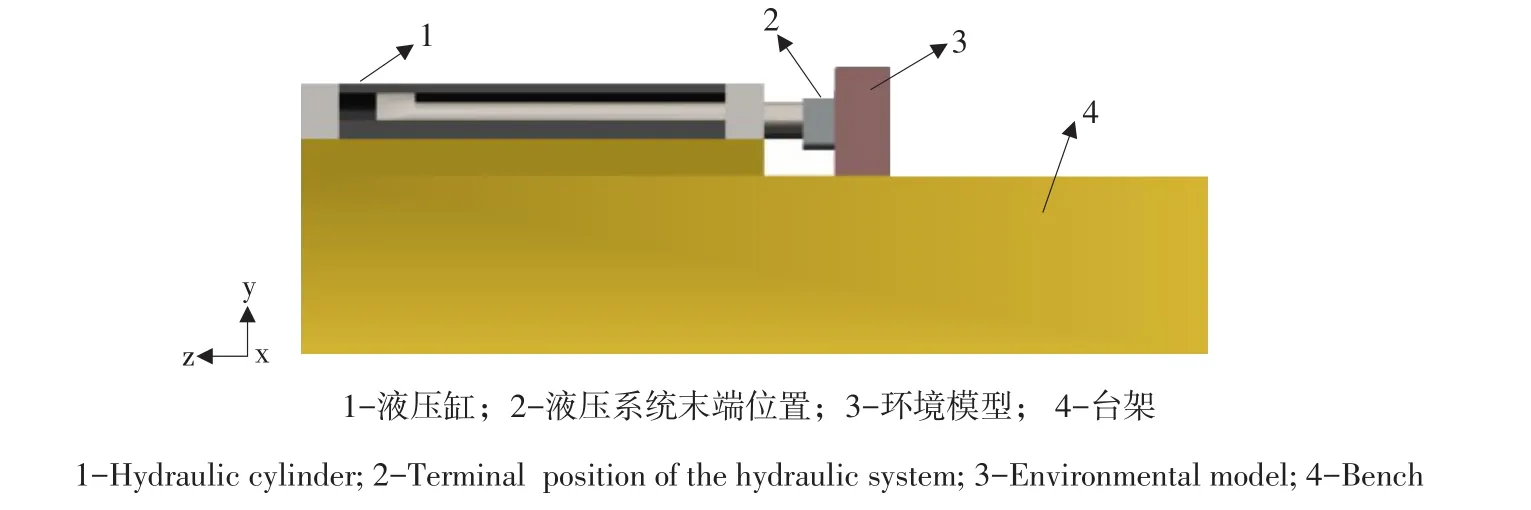
图11 Adams虚拟样机模型Fig.11 Model of Adams virtual prototype

仿真结果如图12所示，通过原始阻抗、自适应阻抗和复合粒子群自适应阻抗控制对比分析；原始阻抗控制力跟踪在150N附近，稳态误差较大；模糊自适应阻抗控制力跟踪约为110N，比较接近目标力，稳态误差相对较小；采用复合粒子群自适应阻抗控制，其末端位置接触力约为100N，对目标力准确跟踪，稳态误差基本消除。

图12 力跟踪仿真测试结果Fig.12 Force tracking simulation test result

通过Adams虚拟样机仿真测试可知，其力跟踪效果优于原始阻抗及模糊自适应阻抗控制，验证复合粒子群自适应阻抗算法对液压伺服系统力跟踪有效性，提高液压伺服系统末端位置力跟踪控制性能，为测试物理样机试验提供理论基础。

4 二连杆串联机构台架试验分析

为验证所设计控制策略在不同环境刚度及变期望力条件下，末端位置力跟踪特性及仿真分析有效性，于哈尔滨工业大学机电工程学院设计铝制二连杆串联机构试验台架，用于液压伺服系统力跟踪控制试验。

4.1 机构及原理

如图13a所示，该串联机构由台架、两个连杆机构和两个液压伺服系统组成，其中液压伺服系统（a）装有位移传感器，负责驱动连杆（1）位置控制；液压伺服系统（b）装有位移传感器与力传感器，既可驱动连杆（2）控制位置，又可控制跟踪。故采用液压伺服系统（b）→连杆（2）试验。动力源为哈尔滨工业大学机电工程学院流体控制实验室研制液压油泵（压力：15～18 MPa），满足试验需要。

试验中，计算机作为上位机，上位机软件为Matlab-2009b，下位机（见图13b）采用研华PC104，用XPC作为实时系统，可较好兼容上位机算法程序；HIT-PC104-HXL-P515用于采集每个关节力/位置传感器信号，并AD转换。HIT-PC104-HX L-P520用于DA转换产生液压阀控制信号；各板卡驱动用嵌入式C++编写S-Function模块。

图13 物理样机试验台架与控制器Fig.13 Test bench of physical prototype and controller physical

4.2 不同环境刚度末端位置力跟踪测试

不同环境刚度力跟踪测试试验过程与3.3仿真分析一致，液压伺服系统（b）驱动连杆（2）作往复摆动并代替液压伺服系统末端位置与环境模型（木块、铝块、铁块及石块）接触，同时根据文献[22]方法计算液压杆伸缩一定距离时对应连杆（2）摆动位置。

从开始至9 s时启动液压伺服控制系统，油源压力加致10 MPa，根据环境模型将试验分为4部分，每部分试验分别原始阻抗、模糊自适应阻抗及复合粒子群自适应阻抗控制3组试验，试验结果如图14所示。

由图14a可知，当环境模型为木块时，原始阻抗控制力跟踪稳态误差较明显（约为119 N），模糊自适应阻抗与复合粒子群自适应阻抗控制基本可跟踪目标力，稳态误差约为0。如图14b～14d所示，当环境模型采用铝块、铁块及石块时，试验结果与3.3仿真结果基本一致，采用复合粒子群自适应阻抗控制液压伺服系统末端位置力跟踪稳态保持在0～1，验证采用复合粒子群自适应阻抗控制液压伺服系统，在不同环境模型时力跟踪效果良好，提高液压伺服系统末端位置在不同环境模型下力跟踪控制性能。

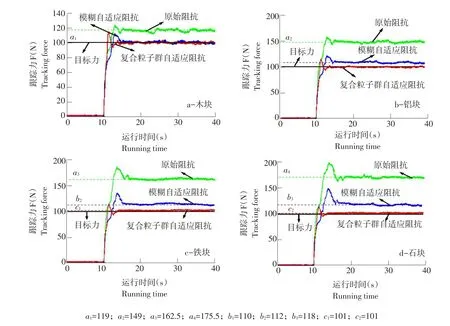
图14 不同环境模型力跟踪试验结果Fig.14 Test result of force tracking simulation

4.3 末端位置变期望力跟踪测试

为验证液压伺服系统在变期望力下跟踪特性，根据4.2测试结果，采用木块作为环境模型，期望力信号位（时间：0～1.4，1.4～3.6，3.6～5 s；力幅值：0，30，10 N）一组方波信号，分别对模糊自适应阻抗及复合粒子群自适应阻抗控制策略对比试验研究，结果见图15。可知，当期望力从0 N阶跃至30 N时，采用模糊自适应阻抗及复合粒子群自适应阻抗控制策略跟踪效果良好，但调节时间分别为1和0.4 s，超调量分别为33.3%和9%；当期望力从30N阶跃至10N时，模糊自适应阻抗控制策略响应时间较慢且存在稳态误差，采用复合粒子群自适应阻抗控制策略，其末端位置力跟踪效果良好，提高液压伺服系统末端位置变期望力跟踪动态性能。

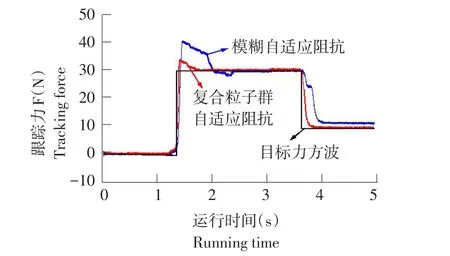
图15 末端位置变期望力跟踪试验结果Fig.15 Rresults of end position of the variable force tracking test

5 结论

a.本文提出一种复合粒子群自适应阻抗控制策略，解决液压伺服系统末端位置在不同环境模型及变期望力下，末端位置力跟踪存在稳态误差及动态特性差问题。根据复合粒子群阻抗控制策略，确定阻抗参数范围基础上，通过3次样条插值拟合建立阻抗参数随环境刚度变化方程，满足系统实时控制需求。

b.分析稳态误差产生原因并建立数学模型，采用自适应算法根据末端位置力和当前位置准确估计环境刚度及环境位置并补偿期望位置。根据环境刚度选择阻抗参数调节，使液压伺服系统末端位置快速准确跟踪期望力。

c.借助Matlab-Adams虚拟样机仿真试验，末端位置力跟踪效果优于原始阻抗及模糊自适应阻抗控制，验证复合粒子群自适应阻抗算法对液压伺服系统力跟踪有效性。

d.通过二连杆串联机构台架不同环境刚度模型及变期望力末端位置力跟踪试验，采用复合粒子群自适应阻抗策略液压伺服系统力跟踪控制，使末端位置能够实时快速、准确跟踪期望力，稳态误差范围为0～1，在期望力发生变化时，其力跟踪动态性能良好。

e.本研究可为液压伺服驱动足式农业机器人在复杂地形行走时保证机身平稳、提高作业性能提供参考，为液压伺服驱动大型农业采摘机械臂末端位置抓取力控制、减少果实破损率等相关研究提供借鉴。

[1] 赵匀,武传宇,胡旭东,等.农业机器人的研究进展及存在的问题[J].农业工程学报,2003,19(1):20-24.

[2] 毕昆,赵馨,侯瑞锋,等.机器人技术在农业中的应用方向和发展趋势[J].中国农学通报,2011,27(4):469-473.

[3] 陈志伟,金波,朱世强,等.液压驱动仿生多足机器人单腿设计与试验[J].农业工程学报,2016,32(5):36-42.

[4] 罗锡文,单鹏辉,张智刚,等.基于推杆电动机的拖拉机液压悬挂控制系统[J].农业机械学报,2015,46(10):1-6.

[5] 徐鹏,崔艳伟,米伯林,等.基于Simulink的牧草收割机液压传动系统仿真研究[J].东北农业大学学报,2011,42(11):83-88.

[6] Pires J N,Godinho T,Araújo R.Force control for industrial applications using a fuzzy PI controller[J].Sensor Review,2004,24(1):60-67.

[7]林君健.基于力传感器的工业机器人主动柔顺装配系统研究[D].广州:华南理工大学,2013.

[8] Sharifi M,Behzadipour S,Vossoughi G.Nonlinear model reference adaptive impedance control for human-robot interactions[J].Control Engineering Practice,2014,32:9-27.

[9] 吴乐彬,王宣银.自适应阻抗控制在广义主动加载中的应用[J].航空学报,2008,29(1):204-208.

[10] 李二超,李战明,李炜.基于视觉的机器人模糊自适应阻抗控制[J].中南大学学报:自然科学版,2011,42(2):409-413.

[11] 刘智光,于菲,张靓,等.基于模糊自适应阻抗控制的机器人接触力跟踪[J].工程设计学报,2015(6):569-574.

[12] 李冰,苏文海,息晓琳,等.仿生四足机器人自适应粒子群优化控制[J].农机化研究,2018,40(5):24-29.

[13]丁庆鹏.基于阻抗控制的四足仿生机器人稳定步态理论及实验研究[D].哈尔滨:哈尔滨工业大学,2016.

[14] 李荣雨,王颖.基于莱维飞行的改进粒子群算法[J].系统仿真学报,2017,29(8):1685-1691.

[15] 王庆喜,郭晓波.基于莱维飞行的粒子群优化算法[J].计算机应用研究,2016,33(9):2588-2591.

[16] 牛海帆,宋卫平,宁爱平.莱维飞行与粒子群的混合搜索算法[J].太原科技大学学报,2016(1):6-11.

[17] 姜长泓,张永恒,王盛慧,等.基于改进粒子群优化算法的PID控制器参数优化[J].应用科学学报,2017,35(5):667-674.

[18] 余胜威,曹中清.基于人群搜索算法的PID控制器参数优化[J].计算机仿真,2014,31(9):347-350.

[19] 胡寿松.自动控制原理[M].6版.北京:科学出版社,2013.

[20] 权龙哲,申静朝,奚德君,等.狭闭空间内苗盘物流化搬运机器人运动规划与试验[J].农业机械学报,2016,47(1):51-59.