基于流固耦合的风力机叶片裂纹扩展机理研究

周 勃，张亚楠，王琳琳，陈长征

（1.沈阳工业大学，辽宁沈阳 110870；2.辽宁省振动噪声控制技术工程研究中心，辽宁沈阳 110870）

1 前言

叶片是风力机获取风能的关键部件，在严苛的自然环境和复杂的载荷共同作用下，叶片经常出现大量裂纹导致风力机维护费用和停机损失剧增，是导致风电成本高昂的主要因素之一［1,2］。风力机叶片常采用复合材料制造，当风力机叶片在加工过程中出现树脂含有孔洞或分布不均、纤维排列不均匀或出现断头、基体与纤维脱胶等损伤形式时，随着叶片结构载荷的增加，就会加剧材料损伤，逐渐出现基体开裂、界面脱粘、层间开裂和纤维断裂等破坏［3］。在很多断裂事故中，断裂是由结构中存在缺陷或裂纹引起的，这种由裂纹所引起的机械部件、结构体的断裂失效，是工程中最常见、最重要的失效模式［4］。裂纹强度因子也是分析裂纹的一个重要标准，Shahani在对环状结构内表面存在的半椭圆裂纹进行有限元分析时，讨论了材料性能、压力等对裂纹应力强度因子的影响［5］。汪泉等基于修正的动量叶素理论，提出了一种新的风力机叶片流固耦合方法，解决了在叶片优化研究过程中气动载荷加载这一关键问题［6］。Oh SY等对风力机叶片复合材料建模进行了论述，但对于风力载荷对叶片的振动失效的影响考虑不足［7］。陈海萍等对叶片流固耦合的应力分布进行了分析与说明，但对叶片周围气流影响范围考虑不是很充分［8］。金雪红等结合K-ω SST湍流模型，对不同风速下的风轮流场分布及压力分布的异同进行了分析，为后续研究提供了良好的拓展思想［9］。

综上所述，目前国内外研究学者对基于流固耦合的风力机叶片结构强度研究还比较少。特别是没有把不同风速下的叶片三维流场分析、流固耦合分析、失效分析和裂纹扩展分析有效地结合起来，尤其是风速产生的气动载荷作用下的复合材料叶片裂纹扩展机理研究很少。

鉴于此，本文利用计算流体力学和断裂力学仿真分析，以I型裂纹为基础，将风力载荷作为裂纹扩展的主要载荷，在叶片最容易产生破坏失效位置嵌套表面半椭圆裂纹，并在不同风速的情况下分析不同初始尺寸裂纹在不同风速的扩展机理。

2 流固耦合理论方程

2.1 计算流体力学基本控制方程

控制方程是物理学守恒定律的数学表达形式，流体在流动过程中要遵守质量守恒定律和动量守恒定律等基本守恒定律。

2.1.1 质量守恒方程

流体流动质量守恒是流体介质流过空间某一控制体V，在相同的时间内，控制体内的质量变化率等于穿过控制体表面S的质量流量。其积分形式表示为：

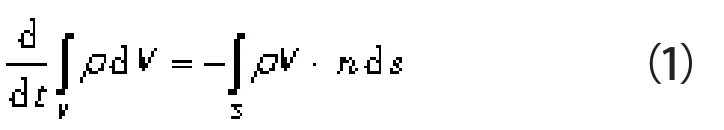
式中 t——流体流动时间

ρ——流体密度

n——单位法向向量

式（1）经过化简变为：

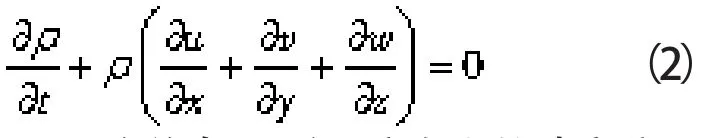
式中 u，v，w——流体在x，y和z方向上的速度分量

此方程也称为连续方程，引入散度表达方式，式（2）可表示为：

式中U——流体速度矢量

风力机叶片流场仿真过程中，将空气视为不可压缩气体，密度ρ为常数，则式（2）变为：

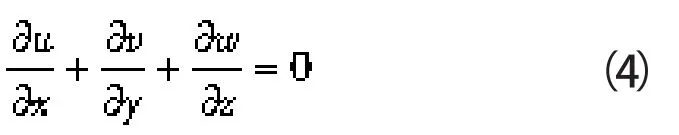
2.1.2 动量守恒方程

动量守恒是从牛顿第二定律发展过来的，可以表述为：控制体中流体的动量对时间的变化率等于外界作用在控制体上的各种力之和。在x，y和z 3个方向的动量守恒方程可表示为：

式中 p——流体控制体上的压力

τxx，τxy，τxz—— 控制体表面上黏性应力τ的分量

Fx，Fy，Fz——控制体上的体力

2.2 流固耦合方程

流固耦合过程在流固耦合交界面处以守恒原则为基础，实现流体和固体之间的数据传递，在不考虑温度传递的情况下，流固耦合交界面处应满足的方程为：

式中 τ——应力

d——位移

f，s——下标，流体和固体

3 裂纹尖端塑性区的应力分析

根据弹性力学，理想线弹性材料的裂纹尖端应力函数U应满足协调方程［10］：

在极坐标系下，裂纹尖端相应的周向正应力σθ、径向正应力σr和剪切应力τ的解析解分别为：

式中 r——径向距离

θ——周向角度

本研究中所预制的裂纹为I型裂纹，此时风力机叶片的裂纹尖端满足如下边界条件：

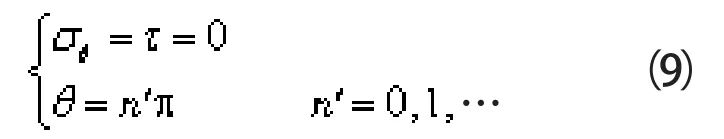
将式（9）带入式（8）可解得：

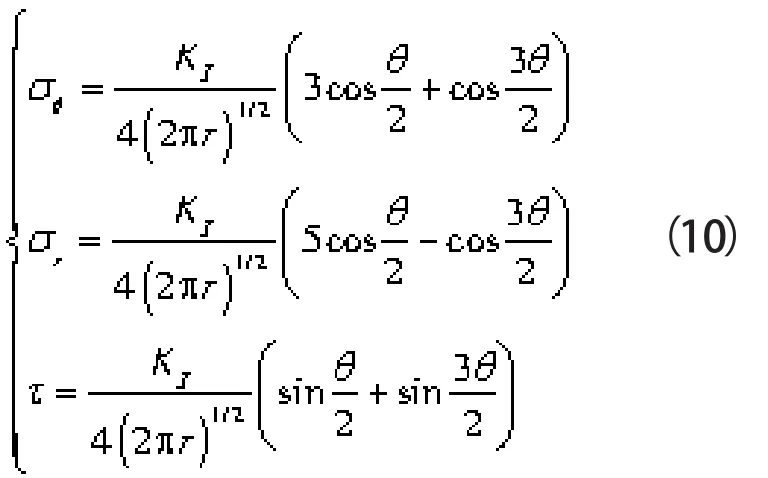
式中 KI—— I型裂纹的应力强度因子，它与坐标系无关，是裂纹尖端应力状态的度量参数

在裂纹的延长线方向（θ=0°）有：

在裂纹的垂直方向（θ=90°）有：

4 风力机叶片裂纹扩展机理研究

4.1 裂纹有限元模型的建立与分析

对于MW级风力机叶片，一般选用具有强度高、重量轻、耐老化、疲劳性能好和低成本特点的无碱型玻璃纤维增强材料（E-Glass），其参数性能如表1所示。叶片采用以环氧树脂和E - 玻璃纤维（Epoxy- E Glass）铺设而成的玻璃钢材料，单层铺层厚度3mm，以单向玻璃纤维布（Epoxy - E Glass - UD）为基础铺设子层纤维布，铺层时以单向玻璃纤维布的纤维方向为基准方向，即0°方向，然后以90°、45°和 -45° 3 个方向交错铺设［11］。

表1 叶片材料参数

文献［12］针对风力机叶片不同位置截面，进行了应力特征分析并得出在0.18R（R为旋转半径）的叶根处易出现应力集中现象，容易出现裂纹损伤，与风力机现实运行中出现的断裂部位相同。

因此本文在距叶根4 m处表面嵌制一横向半椭圆型三维裂纹。其中裂纹长轴为裂纹长度，垂直于叶展方向，短半轴为裂纹深度，垂直于叶片表面如图1所示。

图1 三维表面半椭圆裂纹模型

从图2仿真云图结果可以看出，在裂纹尖端深度方向出现了明显的应力集中，最大集中应力值达到94.7 MPa，远远大于没有嵌套裂纹时叶片上的最大应力值。

图2 裂纹尖端应力云图

对比裂纹尖端应变云图，如图3所示，当裂纹扩展到另一纤维层时，虽然尖端应力较大，但不易在深度方向上继续扩展，而会加大裂纹面张开的角度。

图3 裂纹尖端应变云图

4.2 不同风速下的裂纹扩展机理

通过计算靠近叶根附近表面横向三维半椭圆I型裂纹的应力强度因子KI，可以分析裂纹在不同初始尺寸下的扩展情况。

为进一步分析不同初始裂纹尺寸对裂纹扩展能力的影响，本文以裂纹初始长度不变，当裂纹深度h=1 mm，h=2 mm，h=3 mm，h=4 mm时分别进行裂纹扩展计算。

图4为额定风速V=12 m/s情况下不同深度裂纹前缘KI分布情况。

图4 额定风速下不同深度裂纹前缘KI分布

从图可见，当h=1 mm时，裂尖应力强度因子的值明显大于比裂纹顶端应力强度因子的值，因此表明裂纹深度还有继续增大的趋势。当h=2 mm时，裂纹尖端的应力强度因子的值仍然大于裂纹顶端应力强度的值，但裂尖的应力强度因子开始逐渐增强，表明裂纹开始具有扩展的趋势。当h=3 mm时，裂纹尖端的应力强度因子的值略大于裂纹顶端的应力强度因子的值，而裂尖的应力强度因子的值增大速率明显高于裂纹顶端应力强度因子的增大速率，表明裂纹继续扩展。当h=4 mm时，裂纹尖端的应力强度因子的值与裂纹顶端应力强度因子值的差值开始越来越小，表明此时初始裂纹在深度方向和长度方向上扩展能力相当，裂纹扩展趋于稳定趋势。

为便于分析不同风速下的裂纹扩展机理以及裂纹扩展仿真更加趋于实际情况，预制裂纹参数保证a/b＞2且裂纹扩展初期始终为半椭圆裂纹。设置参数如表2所示。

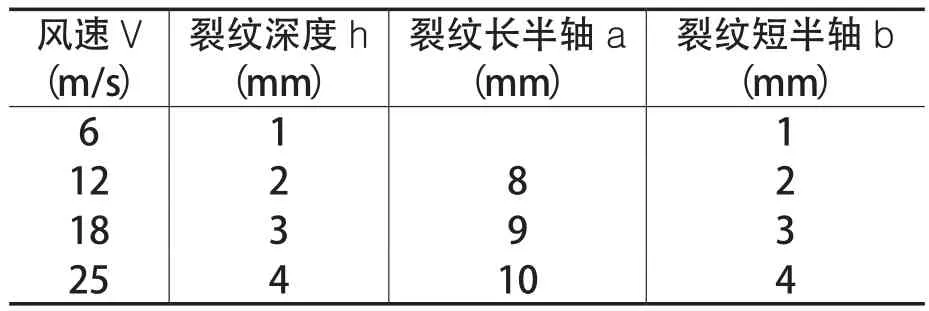
表2 三维裂纹参数

图5仅列出裂纹深度为h=1 mm、h=3 mm、h=4 mm时不同长度裂纹尖端KI随风速的变化关系。从图可见，同一深度裂纹在不同风速下计算出的裂尖KI值随裂纹长半轴的增加几乎不变，表明裂纹初始长度对裂纹深度方向上的扩展能力影响也不是很大，这与文献中的实验结果基本一致［13］。表明本文分析结果的合理性，进一步证明了纤维铺层材料的抗断裂能力。

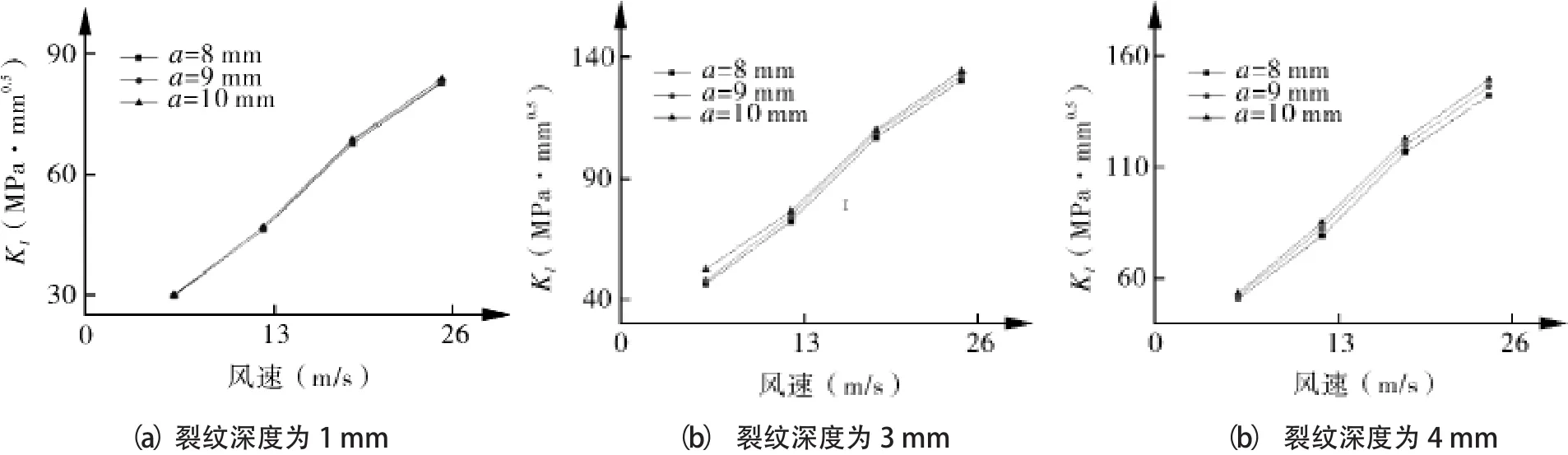
图5 裂纹深度分别为1，3，4 mm时不同长度裂纹尖端KI随风速的变化关系

如图6所示，不同风速下同一裂纹长度计算出的裂尖KI随裂纹深度的增加而增加，当风速高于额定风速时增加幅度逐渐增大，表明初始裂纹深度尺寸增加时会促进裂纹深度方向上的扩展。

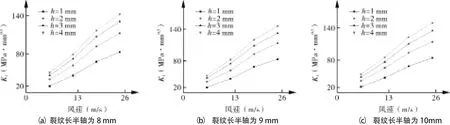
图6 裂纹长半轴分别为8，9，10 mm时不同深度裂纹尖端KI随风速的变化关系

从图5中可以看出当裂纹深度尺寸一定时，随着风速的增加裂纹尖端KI快速增加，对比图6发现风速对初始裂纹深度方向上的扩展起关键作用，在高风速下，裂纹在深度方向上的扩展速率明显增大。在h=4 mm的裂纹尖端应力强度因子KI的值达到了148 MPa·mm0.5，裂纹发生失稳扩展的几率增大。

5 结论

（1）纤维复合材料的韧性对裂纹长度的扩展具有一定的阻碍作用，使裂纹的初始长度对裂纹深度的扩展影响很小。

（2）裂纹强度因子的值随着风速和裂纹深度的增大而增大，表明裂纹的初始尺寸较大时，对裂纹长度方向的扩展有一定促进作用。

（3）裂纹在深度和长度上的扩展速率随着风速的增大而明显增大，且在高风速下，裂纹深度达到4 mm时裂纹发生失稳扩展的几率增大。

［1］ Hameed Z,Hong Y S,Cho Y M,etc.Condition monitoring and fault detection of wind turbines and related algorithms:A review［J］.Renewable and Sustainable Energy Reviews,2009,13:1-39.

［2］ Marin J C,Barroso A,Paris F,et al.Study of damage and repair of blades of a 300kW wind turbine［J］.Energy,2008，33：1068-1083.

［3］ 沈观林，胡更开.复合材料力学［M］.北京：清华大学出版社，2006:120-124.

［4］ 瞿伟廉，鲁丽君，李明.带三维穿透裂纹结构的有限元实体建模方法［J］.武汉理工大学学报，2008，30(1)：87-90.

［5］ Shahani A R.Stress intensity factor calculation of steel-lined hoop-wrapped cylinders with internal semi-elliptical circumferential crack［J］.Engineering Fracture Mechanics,2007,74(13):2004-2013.

［6］ 汪泉，陈进，王君，等.气动载荷作用下复合材料风力机叶片结构优化设计［J］.机械工程学报，2014，50(9)：114-121．

［7］ SY Oh,Lihrescu L.Effects of pretwist and presetting on coupled bending vibrations of rotating thin-walled composite beams［J］.International Journal of Solids and Structures,2003(40):1203-1224.

［8］ 陈海萍，孙文磊，郭健.风力发电机叶片的流固耦合分析［J］.机床与液压，2010，38(19)：79-82．

［9］ 金雪红，梁武科，李常.风速对垂直轴风力机风轮气动性能的影响［J］.流体机械，2010，38(4)：45-49．

［10］ 王自强，陈少华.高等断裂力学［M］.北京：科学出版社，2009.

［11］ 芮晓明，柳亦兵，马志勇.风力发电机组设计［M］.北京：机械工业出版社，2011．

［12］ 赵元星，白叶飞，汪建文，等.风力机叶片在不同载荷作用下的应力特征分析［J］.可再生能源，2015，33(5)：693-699．

［13］ 周勃，陈长征，张宇，等.风力机叶片裂纹的动态扩展特性研究［J］.中国机械工程，2013，24(8)：1108-1113.