高阶方向导数的计算公式及其它

陈麒先, 万正苏



高阶方向导数的计算公式及其它

陈麒先, 万正苏

(湖南理工学院 数学学院, 湖南 岳阳 414006)

利用张量积推导出高阶方向导数的计算公式, 并举例说明高阶方向导数和高阶偏导数之间的关系.

高阶方向导数; 张量积; 计算公式; 高阶偏导数

0引言

科学和工程技术中的许多问题不仅要考虑函数沿各个方向轴的变化率即偏导数, 还需设法求得函数沿任意指定方向的变化率即对指定方向的方向导数. 方向导数是多元函数微分学中的一个重要概念, 是研究多元函数性质的重要手段, 关于其研究的成果很多. 在已有的研究中, 关于高阶方向导数的研究甚少. 文[1]中作者在给出二阶方向导数定义并得到计算公式后, 定义了高阶方向导数, 并探讨了高阶方向导数的应用, 但没有给出高阶导数的计算公式, 因此本文将研究高阶方向导数的计算以及高阶方向导数和高阶偏导数之间的关系.

全文安排如下: 首先利用张量积推导高阶导数的计算公式, 然后举例说明高阶方向导数和高阶偏导数之间的关系.

1 高阶方向导数的计算公式

本节推导高阶方向导数的计算, 为此要用到如下定义和引理.

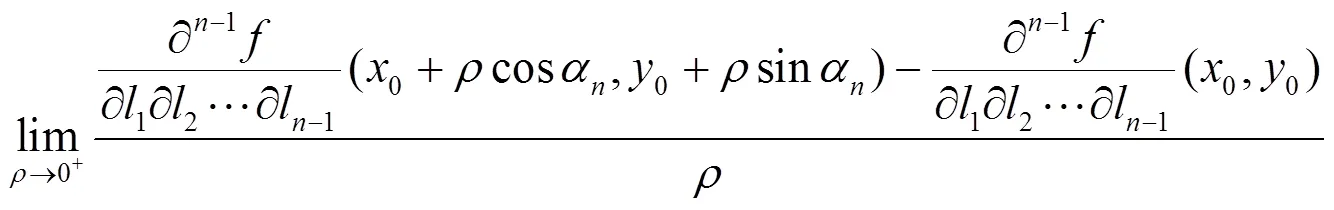
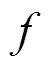
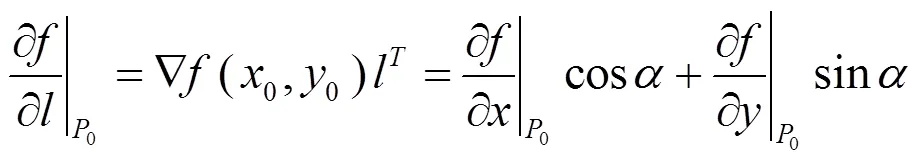
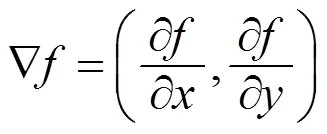
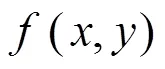
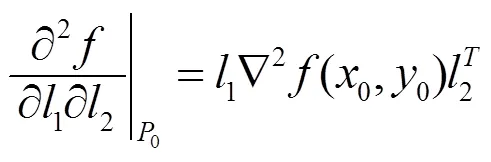
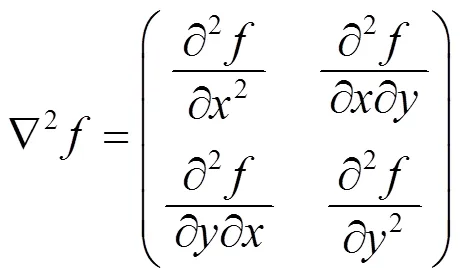
为了得到三阶及三阶以上的方向导数的通用计算公式, 先考虑三阶情形.

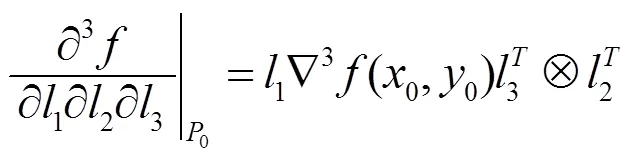
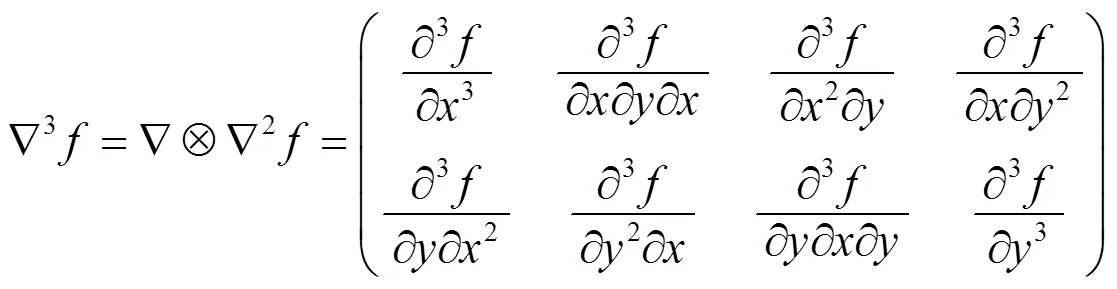
证明由已知条件以及引理1.1和引理1.2可得

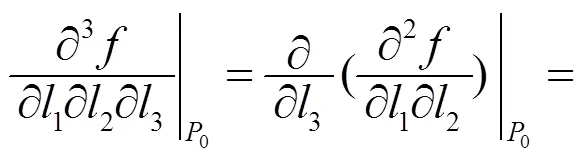
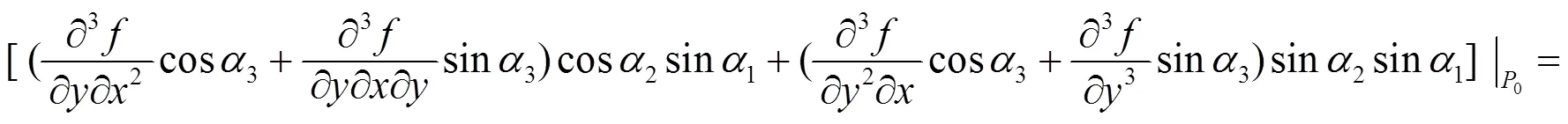
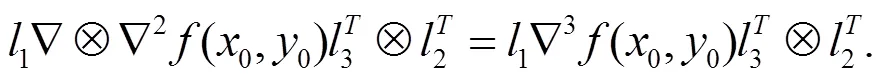
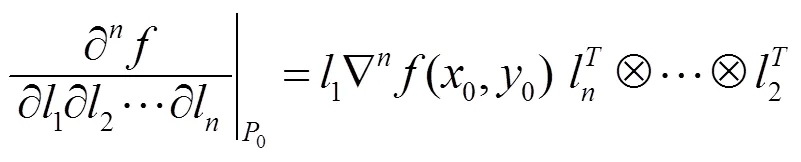
其中

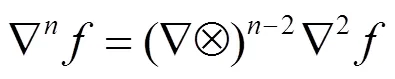
证明采用数学归纳法.

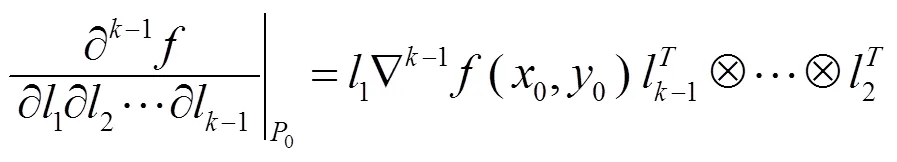
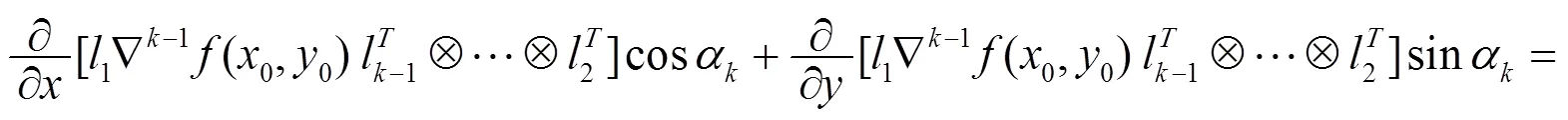
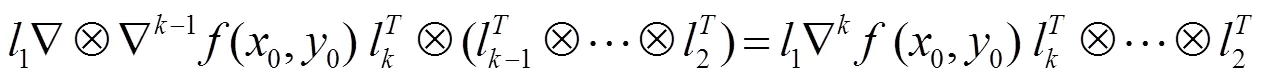
这说明定理1.2仍成立. 故对任意不小于2的自然数, 定理1.2恒成立.

2 高阶方向导数与高阶偏导数的关系

本节主要以二阶情形为例来说明高阶方向导数与高阶偏导数的关系.

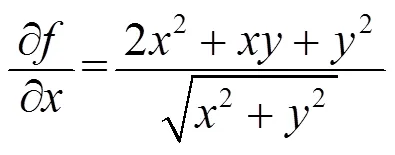
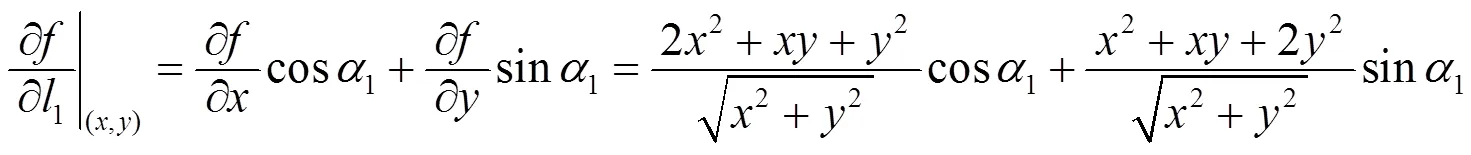
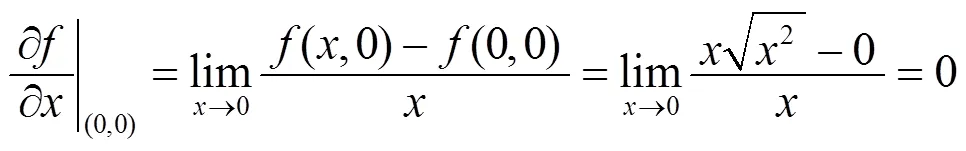
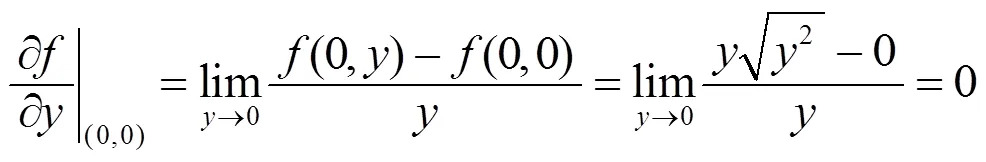
其中

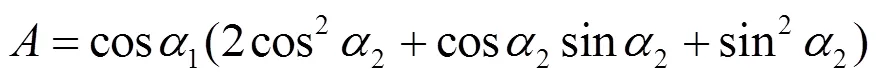
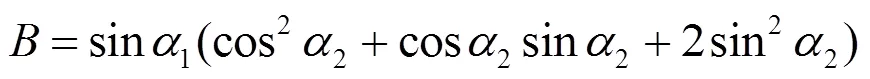
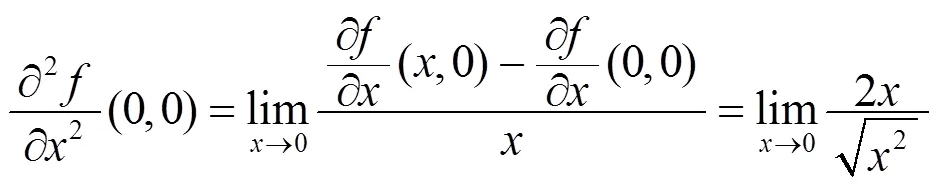
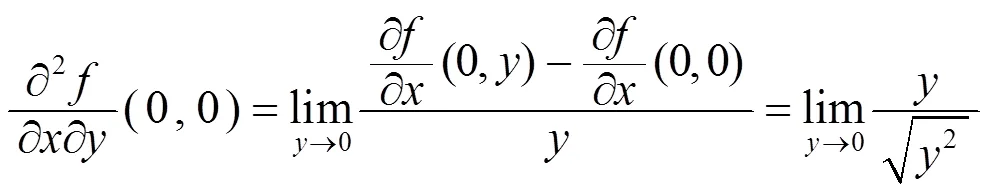
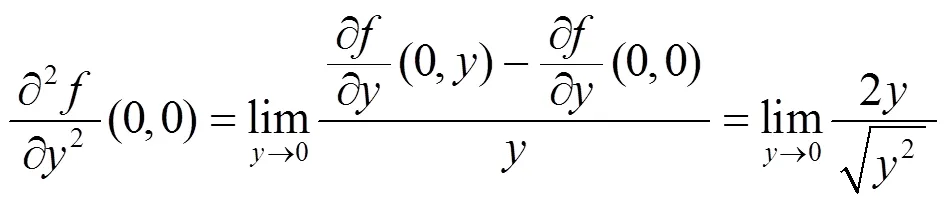
例2 讨论函数

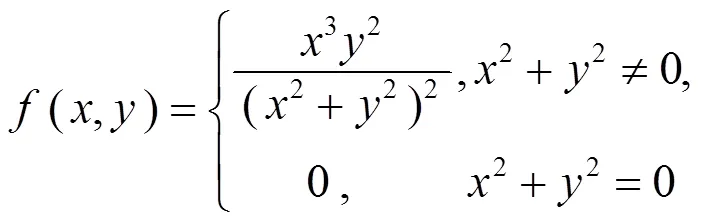
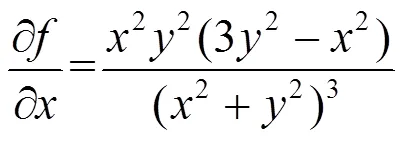
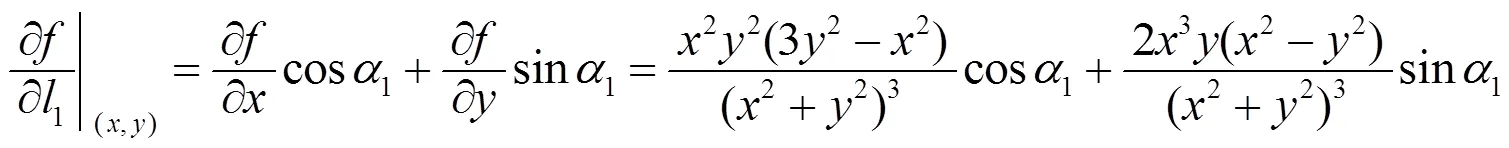
且

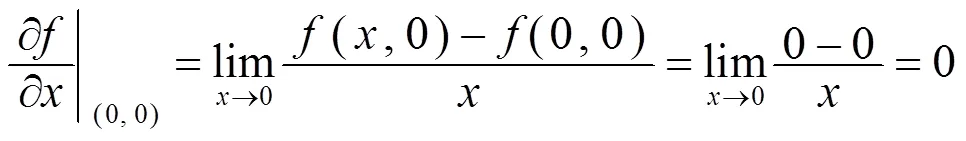
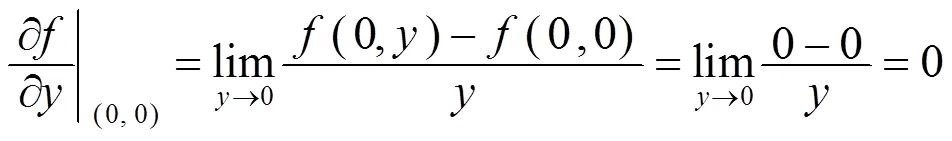
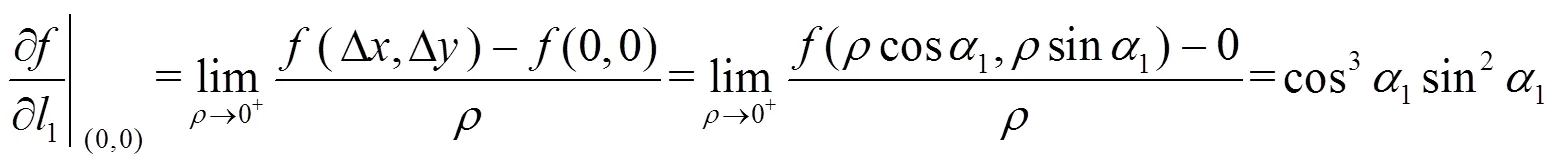
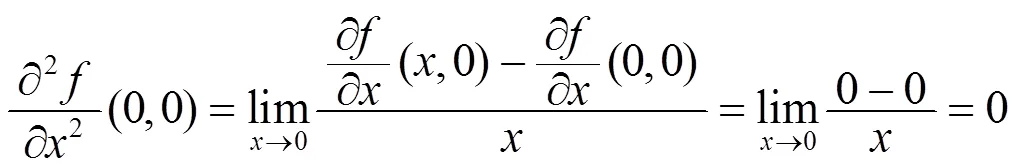
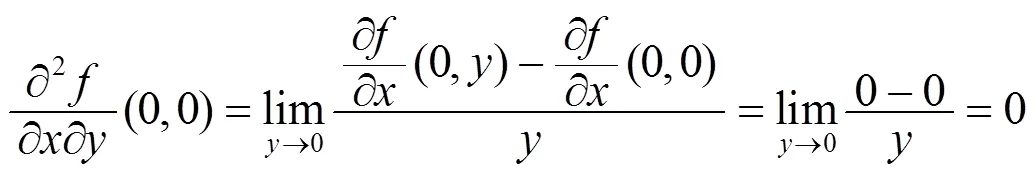
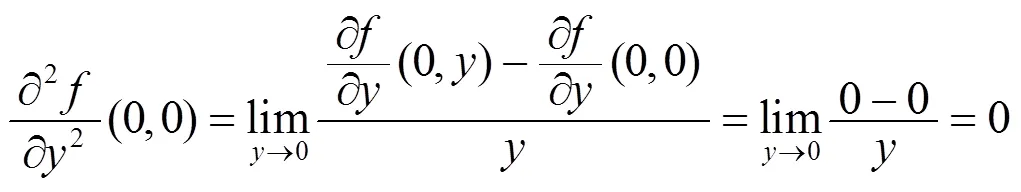
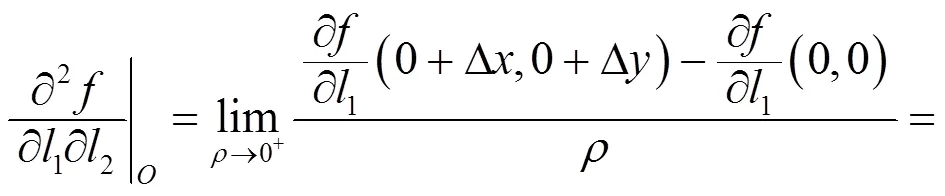
其中

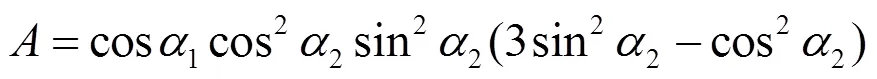
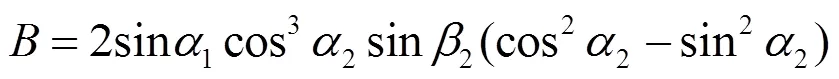
例1说明函数沿任意两个方向的二阶方向导数都存在, 但二阶偏导数不一定存在. 例2说明函数的所有二阶偏导数都存在, 但沿任意两个方向的二阶方向导数不一定不存在. 虽然二阶方向导数的存在性和二阶偏导数的存在性之间没有必然的联系, 但它们之间还是有一定关系的. 事实上, 引理1.2说明所有二阶偏导数存在且连续是沿任意两个方向的二阶方向导数存在的充分条件, 而且若取如下四个方向

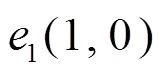
则不难得到下面几个结论.

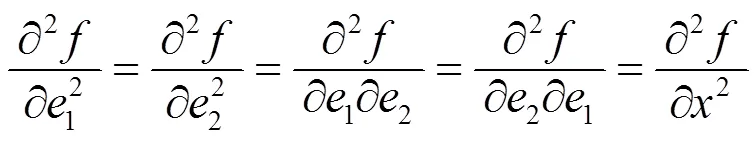
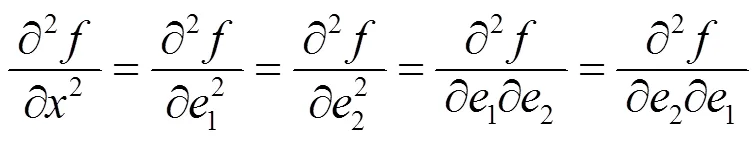
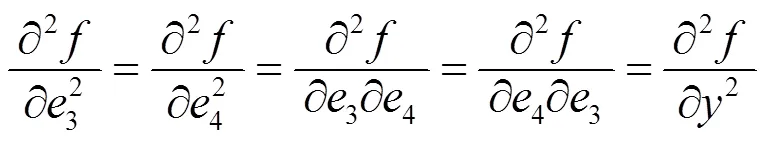
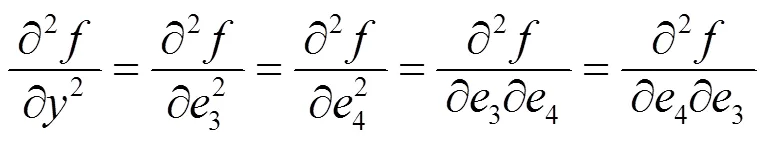
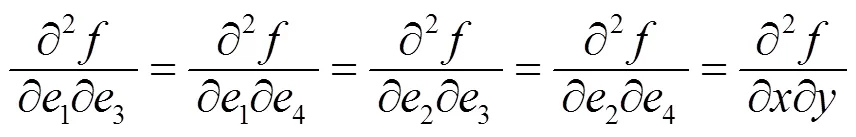
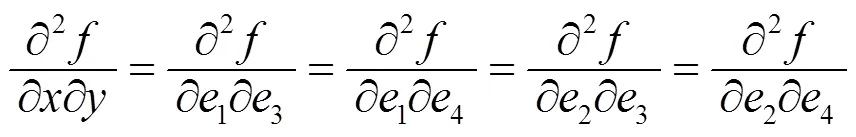
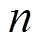
3 结束语

本文推出了高阶方向导数的计算公式, 并研究了二阶方向导数与二阶偏导数之间的关系. 虽然本文的研究都是针对于二元函数的, 但本文的所有结论都可以推广到一般多元函数.

[1] 隋允康. 高阶方向导数及其应用[J]. 北京工业大学学报, 2010, 36(8): 1135~1140

[2] 华东师范大学数学系. 数学分析[M]. 第4版. 北京: 高等教育出版社, 2012

[3] 同济大学数学系. 高等数学[M]. 北京: 高等教育出版社, 2007

A Cumputational Formula for Higher Order Directional Derivatives and Others

CHEN Qixian, WAN Zhengsu

(College of Mathematics, Hunan Institute of Science and Technology, Yueyang 414006, China)

In this paper, we use the vector product to derive a computational formula for higher order directional derivatives. Furthermore, we investigate the relationship between higher order directional derivatives and higher order partial derivatives.

higher order directional derivative, tensor product, computational formula, higher order partial derivative

2017-10-03

陈麒先(1993− ), 男, 湖南宜章人, 湖南理工学院数学学院硕士研究生. 主要研究方向: 数学教育

O172

A

1672-5298(2017)04-0003-05