应用知识进化原理求解背包问题的算法研究

严太山, 郭观七, 李文彬



应用知识进化原理求解背包问题的算法研究

严太山, 郭观七, 李文彬

(1. 湖南理工学院 信息与通信工程学院, 湖南 岳阳 414006; 2. 湖南理工学院 复杂工业物流系统智能控制与优化湖南省重点实验室, 湖南 岳阳 414006)

以知识进化论哲学思想为基础, 提出一种应用知识进化原理求解背包问题的算法(简称为KP-KEA), 利用Banach压缩映射原理证明了算法的全局收敛性. 该算法使用传承算子来传承知识库中的优秀知识个体, 利用创新算子来产生新知识个体, 利用更新算子来更新知识库, 在它们的共同作用下实现知识的进化, 最后从知识库的最优知识个体中获取背包问题的最优解. 实例表明, 该算法在求解背包问题时取得了良好的效果, 其收敛速度和最优解的质量均优于常用的遗传算法. 该算法同样适用于其他约束优化问题的求解.

背包问题求解; 知识进化原理; 全局收敛性分析; 约束优化

0 引言

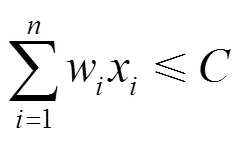
求解背包问题的算法通常有经典算法以及各种生物进化算法[3~8], 目前人们的研究仍然集中在生物自然选择层面上[9,10], 由于算法存在与生俱来的局限性, 在求解大规模背包问题时, 并不一定能得到问题的最优解. 知识进化算法是模拟人类知识进化机理求解复杂问题的一种新方法, 本文将知识进化原理应用于背包问题求解, 建立应用知识进化原理求解背包问题的算法(简称为KP-KEA), 旨在提高背包问题的求解效率.

1 应用知识进化原理求解背包问题的算法思想

应用知识进化原理求解背包问题的算法(KP-KEA)是建立在卡尔·波普尔的知识进化论[9~15]基础上的. 卡尔·波普尔的知识进化论告诉我们, 知识也是不断进化的, 知识进化具有与生物进化相似的进化机理, 包含了新知识的产生机制和优胜劣汰的自然选择机制.

KP-KEA的基本思想是: 通过分析实际领域问题, 建立待求解问题的初始知识库; 然后利用知识进化算子, 即传承算子、创新算子和更新算子, 来执行知识进化操作, 包括传承优秀知识个体、产生新的知识个体和更新知识库; 算法满足结束条件时, 知识库中的最优知识个体就是问题的最优解. 其算法流程如图1所示.

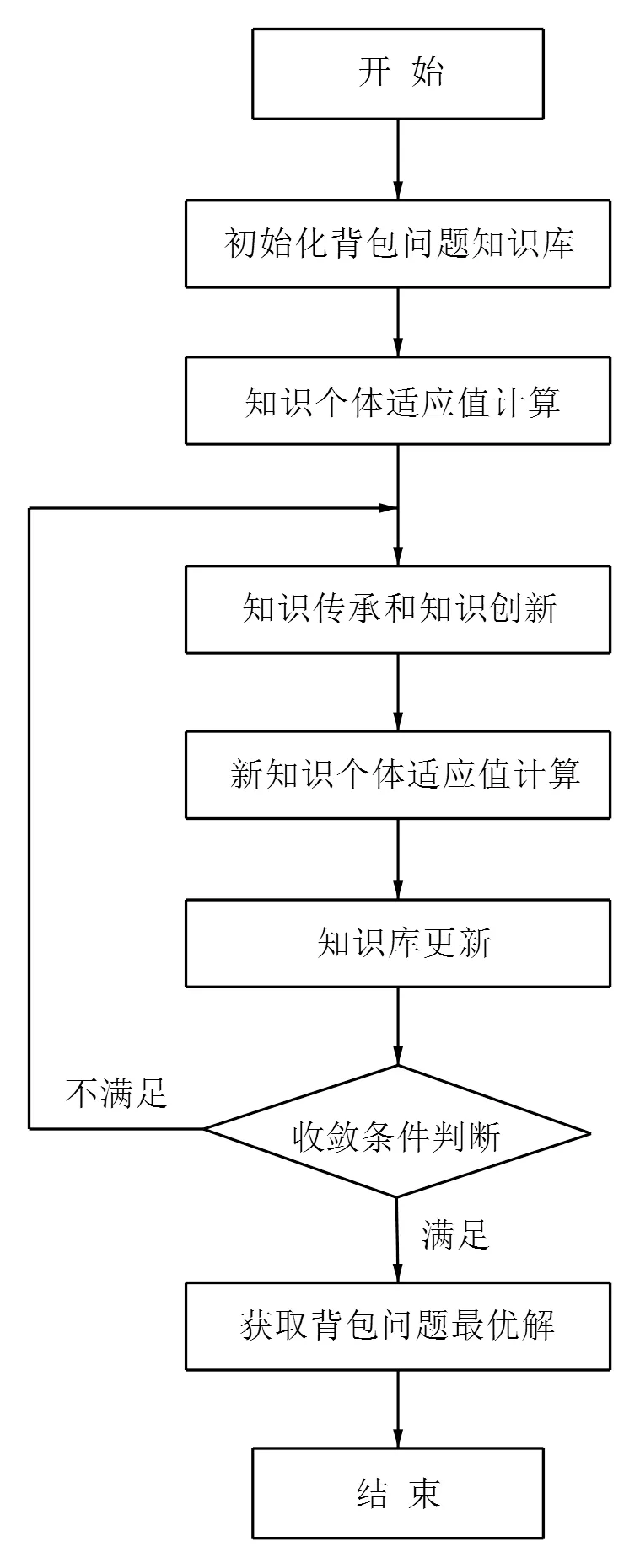
图1 KP-KEA算法流程

2 应用知识进化原理求解背包问题的算法实现

2.1 知识库的结构及知识个体编码方法

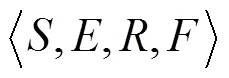
2.2 进化算子

2.2.1传承算子

传承算子的作用是从知识库中选择规模固定的优秀知识个体进入进化池中. 本文采用罚函数法来处理背包问题的约束, 评价知识个体优劣的适应值函数为

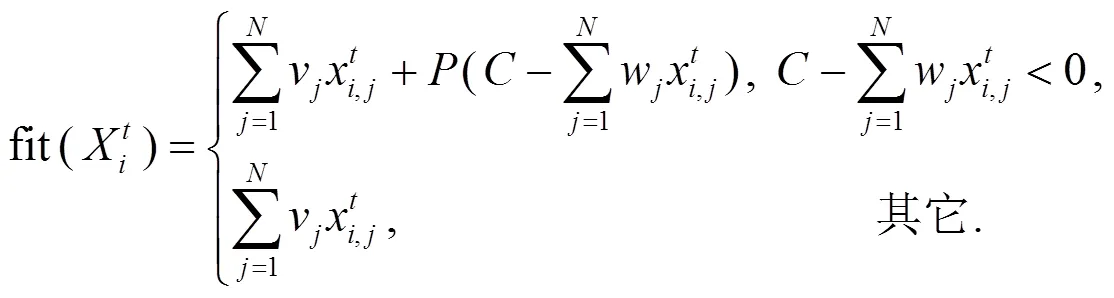
2.2.2创新算子

创新算子的作用是产生新的知识个体, 具体包括以下两个方面:

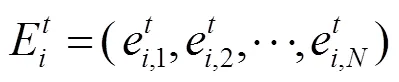
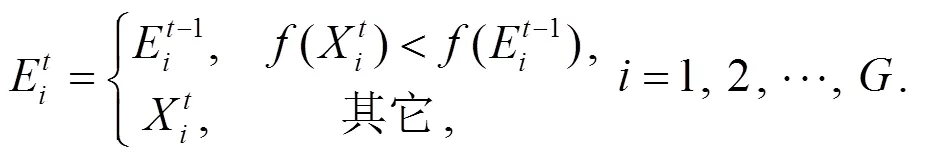
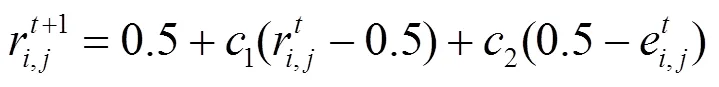
②对问题可行解的创新, 即根据当前代的认知度对知识个体中的可行解部分进行调整. 创新规则为

2.2.3更新算子

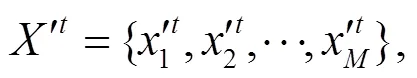
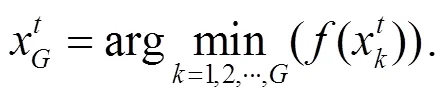
知识库更新规则为

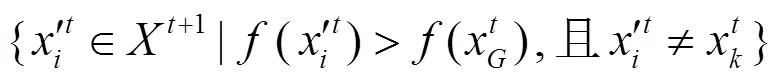
3 应用知识进化原理求解背包问题的算法收敛性分析

3.1 基本概念与定理

本节相关概念与结果见文[16~18].

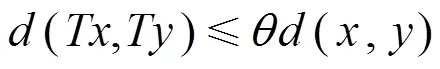
3.2 应用Banach压缩映射原理分析KP-KEA的收敛性

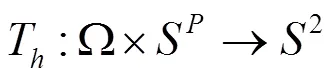
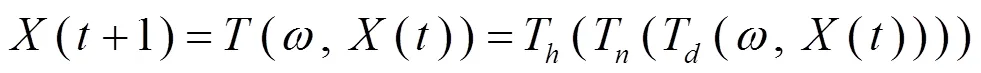
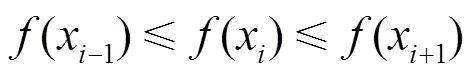
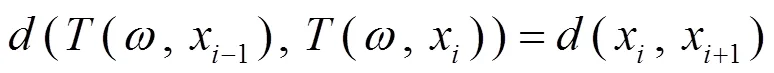
4 应用实例

为了测试算法的性能, 我们选取如下两个背包问题实例进行求解.

表1 GA和KP-KEA对实例1的求解结果

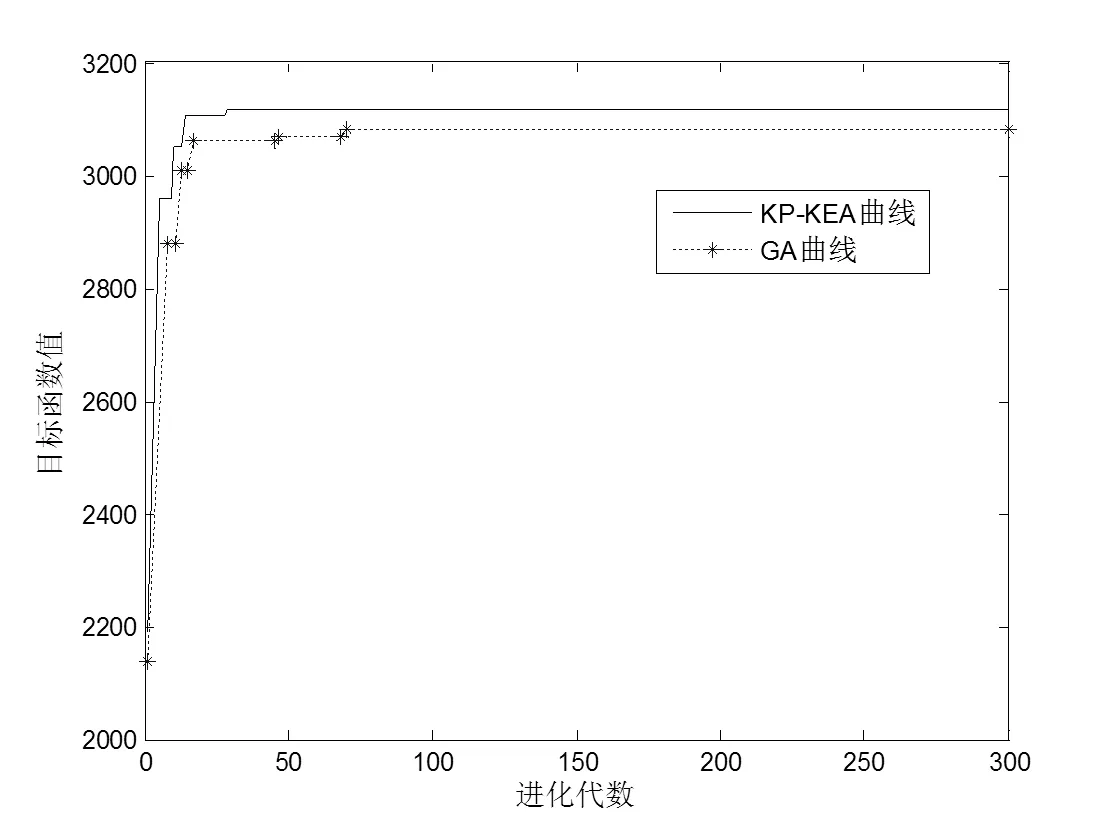
图2 GA和KP-KEA求解实例1的收敛曲线

表2 GA和KP-KEA对实例2的求解结果

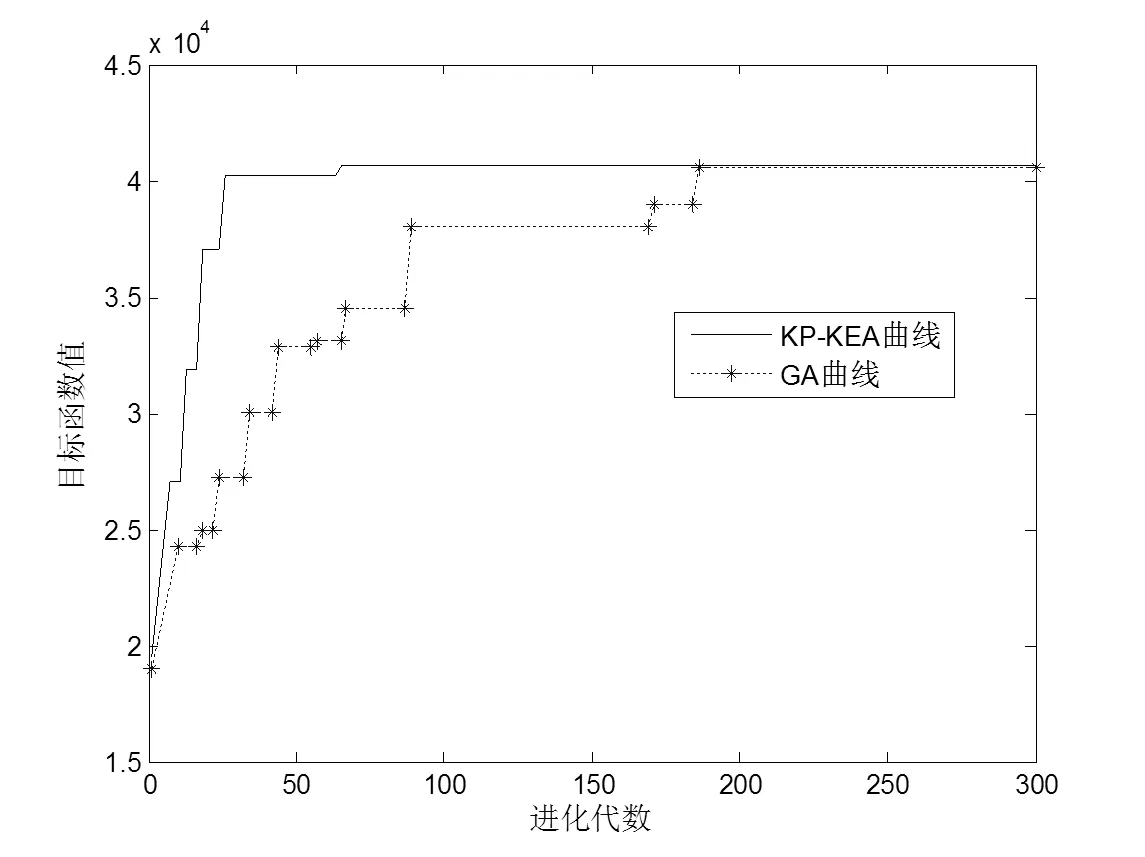
图3 GA和KP-KEA求解实例2的收敛曲线

从表1、表2和图2、图3中的结果可以看出, 在求解背包问题时, 无论是在解的质量方面, 还是在收敛速度方面, KP-KEA比遗传算法都要优越.

5 结论

以知识进化原理为基础, 建立了一种背包问题求解算法(KP-KEA). 在理论上应用Banach压缩映射原理证明了该算法具有很好的全局收敛性; 算法在对背包问题实例进行优化求解时, 表现出了良好的寻优性能, 能以较少的迭代次数寻找到全局最优解. 今后可以使知识进化原理与各种传统的生物进化算法进行融合应用, 以拓宽其工程应用领域.

[1] Sinnamon R M, Andrews J D.[J]. Reliability Engineering and System Safety, 1997, 58(2): 89~96

[2] Lee Hae Sang, Lie Chang Hoon.[J]. IEEE Trans. on Reliability,1997 , 46 (3): 360~363

[3] 贺毅朝, 宋建民, 张敬敏. 利用遗传算法求解静态与动态背包问题的研究[J]. 计算机应用研究, 2015, 32(4): 1011~1015

[4] 刘寒冰, 张亚娟. 求解0-1背包问题的改进混合遗传算法[J]. 计算机系统应用, 2015,24(6): 197~201

[5] 余 娟, 冯晓华, 贺昱曜. 求解多维背包问题的改进分布估计算法[J]. 计算机仿真, 2014, 31(10): 286~290

[6] 张 晶, 吴虎胜. 求解背包问题的病毒进化蝙蝠算法[J]. 计算机仿真, 2015, 32(6): 256~261

[7] 杨 震, 马天宝, 余 文. 广义分子计算模型在0-1背包问题中的应用[J]. 计算机科学, 2014, 41(s2): 7~9

[8] 黄席樾, 张著洪. 现代智能算法理论及应用[M]. 北京: 科学出版社, 2005

[9] 刘纯青, 杨莘元, 张 颖. 知识进化策略[J]. 系统工程与电子技术, 2007,29(6): 1017~1020

[10] 黄海燕, 顾幸生, 刘曼丹. 求解约束问题的文化算法研究[J]. 自动化学报, 2007, 33(10): 1115~1120

[11] 朱祖平. 知识进化与知识创新机理研究[J]. 研究与发展管理, 2000, 12(6): 16~19

[12] 钟义信. “信息-知识-智能”生态意义下的知识内涵与度量[J]. 计算机科学与探索, 2007, 1(2): 129~137

[13] 舒炜光, 卓如飞. 客观知识——一个进化论的研究[M]. 上海: 上海译文出版社, 2005

[14] 傅季重, 周昌忠, 蒋 戈. 猜测与反驳——科学知识的增长[M]. 上海: 上海译文出版社, 2005

[15] 马慧民, 叶春明, 张 爽, 等. 基于知识进化算法的生产采购协同计划问题研究[J]. 计算机应用研究, 2009, 26(12): 4621~4623

[16] 李敏强, 寇纪凇, 林 丹, 等. 遗传算法的基本理论与应用[M]. 北京: 科学出版社, 2002

[17] 许天周. 应用泛涵分析[M]. 北京: 科学出版社, 2002

[18] Bryan P.Rynne Martin A. Youngson.[M]. Beijing: Tsinghua University Press, 2005

An Algorithm for Solving Knapsack Problem by Knowledge Evolution Principle

YAN Taishan, GUO Guanqi, LI Wenbin

(1.College of Information and Communication Engineering, Hunan Institute of Science and Technology, Yueyang 414006, China; 2. Key Laboratory of Hunan Province on Intelligent Control and Optimization of Complex Industrial Logistics System, Hunan Institute of Science and Technology, Yueyang 414006, China)

Based on the evolutionary epistemology idea, an algorithm (called KP-KEA) is proposed for solving knapsack problems by knowledge evolution principle. The global convergence of this algorithm is proved by using the Banach contraction mapping principle. In this algorithm, inheritance operator is used to inherit excellent knowledge individuals, innovation operator is used to produce novel knowledge individuals, and update operator is used to update knowledge-base. Knowledge evolution is realized by these three operators accordingly. Finally, the optimal solution of knapsack problems can be gained from the optimal knowledge individual. The successful experimental results show that this algorithm is effective to solve knapsack problems. Compared with genetic algorithm, the convergence speed and the optimal solution’s quality of this algorithm are all better. This algorithm is suited to solve other constraint optimization problems too.

knapsack problem solution, knowledge evolution principle, global convergence analysis, constraint optimization

2017-08-16

湖南省自然科学基金项目(2017JJ2107); 湖南省科技计划项目(2016TP1021); 湖南理工学院研究生课程建设项目(201505)

严太山(1968− ), 男, 湖南祁东人, 博士, 湖南理工学院信息与通信工程学院副教授. 主要研究方向: 进化计算、智能信息处理

TP301.6

A

1672-5298(2017)04-0008-06