探析物理课题研究——六w法则

陈 钺, 柳建国



探析物理课题研究——六w法则

陈 钺, 柳建国

(湖南理工学院 物理与电子学院, 湖南 岳阳 414006)

以滑块平面运动为研究课题, 阐述研究、学习、应用物理知识时必须回答的六个问题, 即六个“w”: “who？”选择研究对象; “what is it？”建立物理模型; “when？”何时, “where？”何处, 建立物理环境模型; “what is it doing？”建立物理过程模型; “why-how do we deal with？”发现问题, 提出疑问, 寻求解决方法. 引导探索精神, 培养创造性思维.

滑块; 滑动; 光滑; 物理实验; 物理模型

物理学是一门实验科学, 是对自然现象的观察, 分析; 并进行模拟实验, 寻求物理概念以及物理概念之间的关系——定律、定理, 形成理论体系.

物理学的研究、学习、应用过程如图1所示.

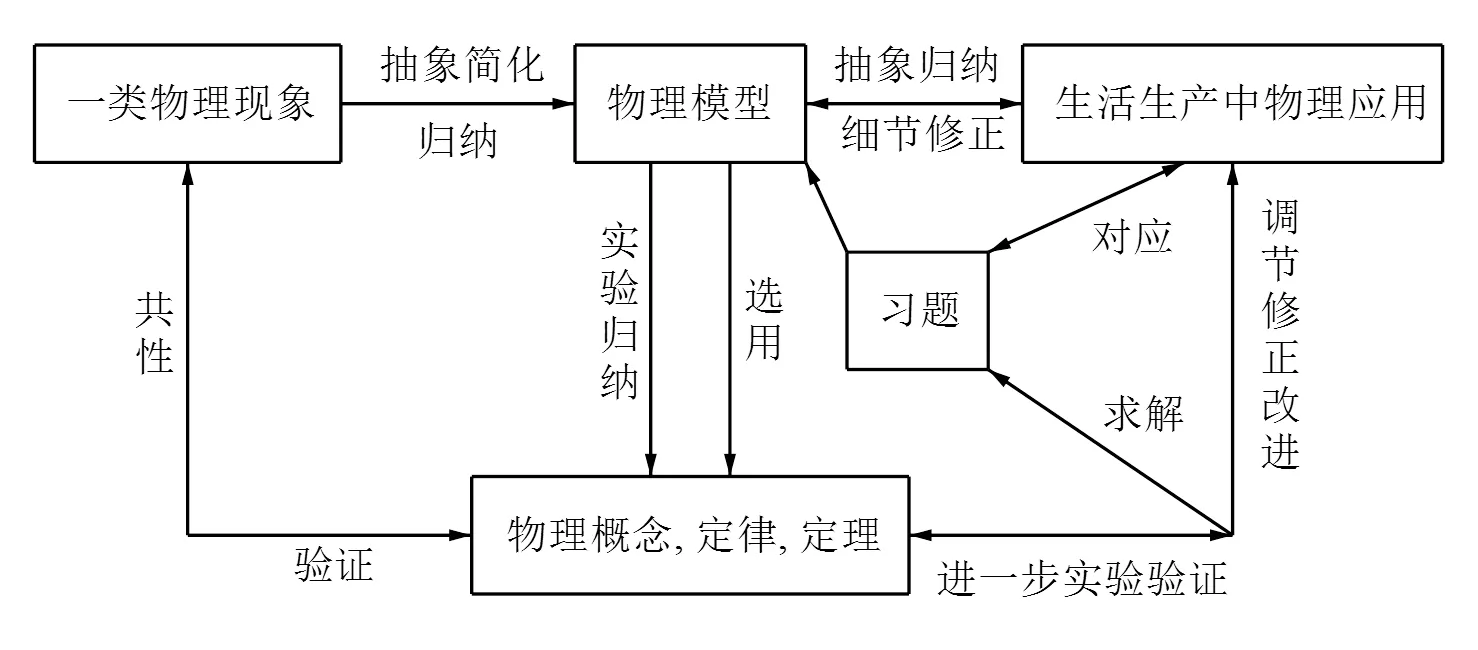
图1

从图1可见: “实验”是其灵魂, 实际物理现象是基本元素, 连习题也具有其背景, 而物理模型则是核心.

笔者以“滑块的平面运动”这一经典物理课题为例, 形象地描述图1全过程. 我们将发现研究、学习、应用物理知识过程就是在回答六个问题: 六个“w”.

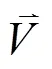
图2

1. 经典常规求解过程

(1) 一“w”(who？): 选定研究对象.整个物理系统仅滑块运动, 取小滑块为研究对象.

(2) 二“w”(what is it？): 建立研究对象的物理模型, 小滑块平动可取其为质点模型(下文称为质点).

(3) 三“w”与四“w”(when？where？): 何时？何处？分析质点运动全过程各时段所处外部物理环境, 建立物理环境模型.

① 处均匀重力场中, 质点受重力作用, 具有重力势能.

②刚性光滑平面所形成的二面角.

(4) 五“w”(what is it doing？): 质点在干什么？建立质点运动的物理过程模型.

经典常规求解过程, 选取建立纯平面滑动物理过程模型.

(5) 分析这五个“w”后开始求解:

质点运动全过程仅保守内力(重力)做功, 故机械能守恒(取水平面为零重力势能参考平面).

2. 六“w”(why？)为什么？

这第六个“w”是物理研究、学习、应用的关键. 具有极其丰富多彩的内容, 推动着物理学科的不断完善进步, 也不断开创新的研究领域, 创造新的物理理论, 推进着物理在各领域的广泛应用.

只要看了物理学发展史就可以看到这“why”的巨大功绩——“科学技术是第一生产力”(why how do we deal with？) 为什么, 我们怎么办？

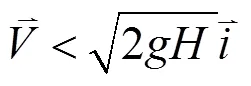
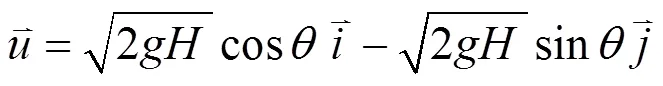
故第五个“w”(what is it doing？)答案应为: 质点运动物理过程模型, 沿斜面加速下滑(滑动物理过程模型)到达点与水平面发生碰撞(完全非弹性斜碰物理过程模型), 再沿水平面滑动(滑动物理过程模型)才是正确的.

4. 质点在非光滑平面二面角运动, 应用纯滑动物理过程模型是否可以正确解决问题？why？提出新问题.

第五个“w”(what is it doing)应怎么正确回答？面对二个“why？”我们用实验寻找答案.

(1) 文[2]研究如图2所示非光滑二面角上小滑块的运动, 设定小滑块与斜面、水平面间的滑动摩擦系数均为, 设计一组实验:

使斜面倾角改变, 而滑块静置高度恒为, 采用纯滑动物理过程模型研究:

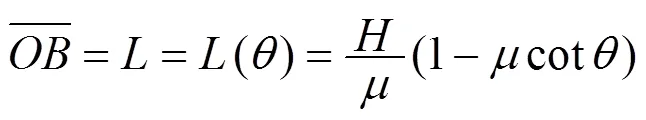
(2)文[2]进一步深入实验分析:

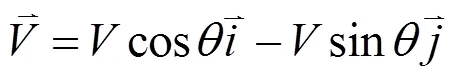
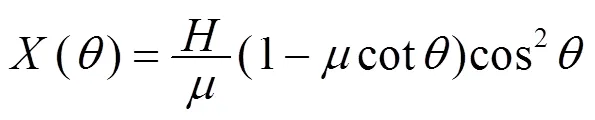
这一结论则与实验结论完全相合, 为实验证明其正确性. 可见当小滑块运动在越过二平角棱线时必然发生了一次完全非弹性碰撞.

5. 文[1]、[2]总结: 滑块在重力场中沿两光滑平面组成的二面角运动时, 应采用滑动物理过程模型与完全非弹性斜碰物理模型的组合描述, 机械能并不守恒.

但立体二面角形成多样, 并非只有如图2所示一类情况, 也非只有下滑的情况. 上述结论普适吗？

我们又面临一个新的“why-How do we deal with？”文[3]“小滑块运动综合研究”分析, 论述小滑块在各类型立体二面角上运动的各种形式, 证明: 当小滑块越过二面角棱线时均会发生一次完全非弹性斜碰, 只要存在滑块越过二面角棱线这一情况, 机械能就不守恒.

6. 图2所示模型正描述了实际生产工艺流程中的运输装置: 高的出料口, 用斜板接到水平运输皮带上, 为什么出料口加接斜板？

(1)可利用“料”(谷、米、麦、煤、矿粉等)下泄重力势能转化为动能方便水平运输, 节能.

(2)使“料”不直接冲击皮带, 否则长期冲击造成机械损耗.

该“料”为大量小滑块连续下滑, 由上文可知, 其滑下斜板与水平皮带还是发生了完全非弹性碰撞, 耗了能也冲击了水平皮带. 怎么改进装置才能节能, 减耗？

又是一个“why？”(why-how do deal with？)出现了.

文[1]指出: 可将出料口斜板改造为其下端有一圆柱面与水平皮带水平光滑相吻, 则可解决. 这样我们用物理知识提出了一个节能减耗的合理建议.

[1] 陈 钺, 柳建国. 滑块运动再研究[J]. 湖南理工学院学报, 2014, (27)

[2] 陈 钺, 柳建国. 小滑块在非光滑平面上运动再研究[J]. 湖南理工学院学报, 2015, (28)

[3] 陈 钺, 柳建国. 小滑块运动综合研究[J]. 湖南理工学院学报, 2016, (29)

[4] 梁绍荣. 普通物理学第一分册力学[M] . 第3版. 北京: 高等教育出版社, 2010

Analysis of Physical Research Projects: Six “W” Principle

CHEN Yue, LIU Jianguo

(College of Physics and Electronics, Hunan Institute of Science and Technology, Yueyang 414006, China )

Taking the plane motion of the slider as a research topic, we discuss the six problems that must be answered when applying physics knowledge and studying, namely six "w": "who?" choosing the subject of study; "what is it?" building a physical model; "when?", “where?” to build the physical environment model; "what is it doing?” building a physical process model; "why - how do we deal with?” identify problems, ask questions, and seek solutions. Guiding the spirit of exploration and cultivating creative thinking.

slider, sliding, smooth, physical experiment, the physical model

2017-07-10

陈 钺(1947− ), 男, 江苏无锡人, 湖南理工学院物理与电子学院副教授. 主要研究方向: 电磁场理论、物理教学与研究

O313

A

1672-5298(2017)04-0014-03