大地电磁三维正演聚集多重网格算法
2018-01-25殷长春邓居智
陈 辉,尹 敏,殷长春,邓居智
1.吉林大学地球探测科学与技术学院,长春 130026 2.东华理工大学放射性地质与勘探技术国防重点学科实验室,南昌 330013
0 引言
经过几十年的发展,大地电磁三维正演已基本趋于成熟[1-3]。其基本步骤一般为:先对已知电阻率或电导率模型的整个求解区域进行结构或非结构性离散,然后利用有限差分法(FD)[4-7]、有限体积法(FV)[8-10]、有限单元法(FE)[9-15]、积分方程法(IE)[16-18]等数值方法对双旋度磁场或电场方程或矢量和标量势耦合方程进行离散,并施加边界条件得到庞大的稀疏复数线性方程组。对于该线性方程组,通常先采用预处理方法降低矩阵的条件数(比如不完全LU分解[19]、不完全Cholesky分解[20]等),然后采用Krylov子空间迭代方法进行求解,如双共轭梯度法(BICG)[21]、准残量最小化法(QMR)[22]、最小残量法(MRM)[23]等。并利用散度校正技术能够减小迭代次数,加快正演速度,提高计算精度,特别在低频时可取得明显效果[24-25]。另外,随着矩阵排序技术和计算机性能的提高,直接求解技术也逐步应用于线性方程组求解。2009年,Streich[26]利用MUMPS数学求解库在并行机计算机上直接求解该线性方程组,实现电磁法三维正演计算。2016年,Puzyrev等[27]对各种直接求解数学库在地球物理电磁正演模拟中的应用效果和计算效率进行系统分析。但是,直接求解算法对计算机内存及计算机性能要求较高,传统迭代算法随着模型尺度的增大,迭代次数和求解时间急剧增加,均难以满足大规模大地电磁三维正演问题需求。多重网格(MG)法目前已发展成为大型稀疏线性方程组迭代求解的最有效方法之一,在地球物理电磁问题中得到应用[28-30]。该方法可分为几何多重网格(GMG)法和代数多重网格(AMG)法。AMG法是在GMG法原理上建立起来的一种求解矩阵方程的迭代方法,它不依赖于待求解问题的几何和物理属性,仅利用离散后的系数矩阵信息即可对线性方程组进行求解[31]。为了改善AMG算法的稳定性和适用性,2010年,Yvan Notay[32]提出了利用矩阵图论思想的光滑聚集构建方法以实现AMG的粗化(简称AGMG),对算法的基本原理和计算效率进行了详细阐述,并在对流扩散方程和椭圆方程求解应用中实现了并行计算。
本文引入新型代数多重网格算法——聚集多重网格(AGMG)算法求解大地电磁三维正演问题,通过典型地电模型计算验证方法的有效性,通过对不同尺度和不同地电模型的数值模拟分析AGMG及AGMG预处理技术的计算效率,为大地电磁法三维大规模、高精度和快速正演模拟提供技术支撑。
1 大地电磁三维有限体积正演
由大地电磁法理论可知,在忽略位移电流的条件下,麦克斯韦方程组的积分形式为
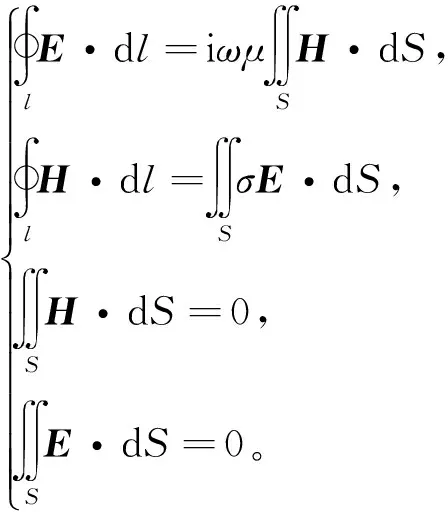
(1)
式中:假定电磁场随时间变化的因子为e-iωt;l为环路线积分步长;S为面积分单元;μ为磁导率;σ为电导率;ω为角频率;E为电场;H为磁场。
在笛卡尔坐标系中采用正六面体网格剖分,每个单元采用Yee氏交错网格进行采样(图1)。电场分量定义在六面体每个边的中点;磁场分量定义为六面体的面中心,方向与面的法向一致。对方程组(1)第一式和第二式采用有限体积进行离散,并消去磁场得到电场的线性方程组:
Ae=b。
(2)
式中:A为大型复稀疏矩阵;e为待求的电场分量;b为与边界条件有关的右端项。边界条件采用第一类的Dirichlet边界条件。为了提高方程组(2)的求解速度和精度,通常在迭代求解过程中施加散度校正技术。
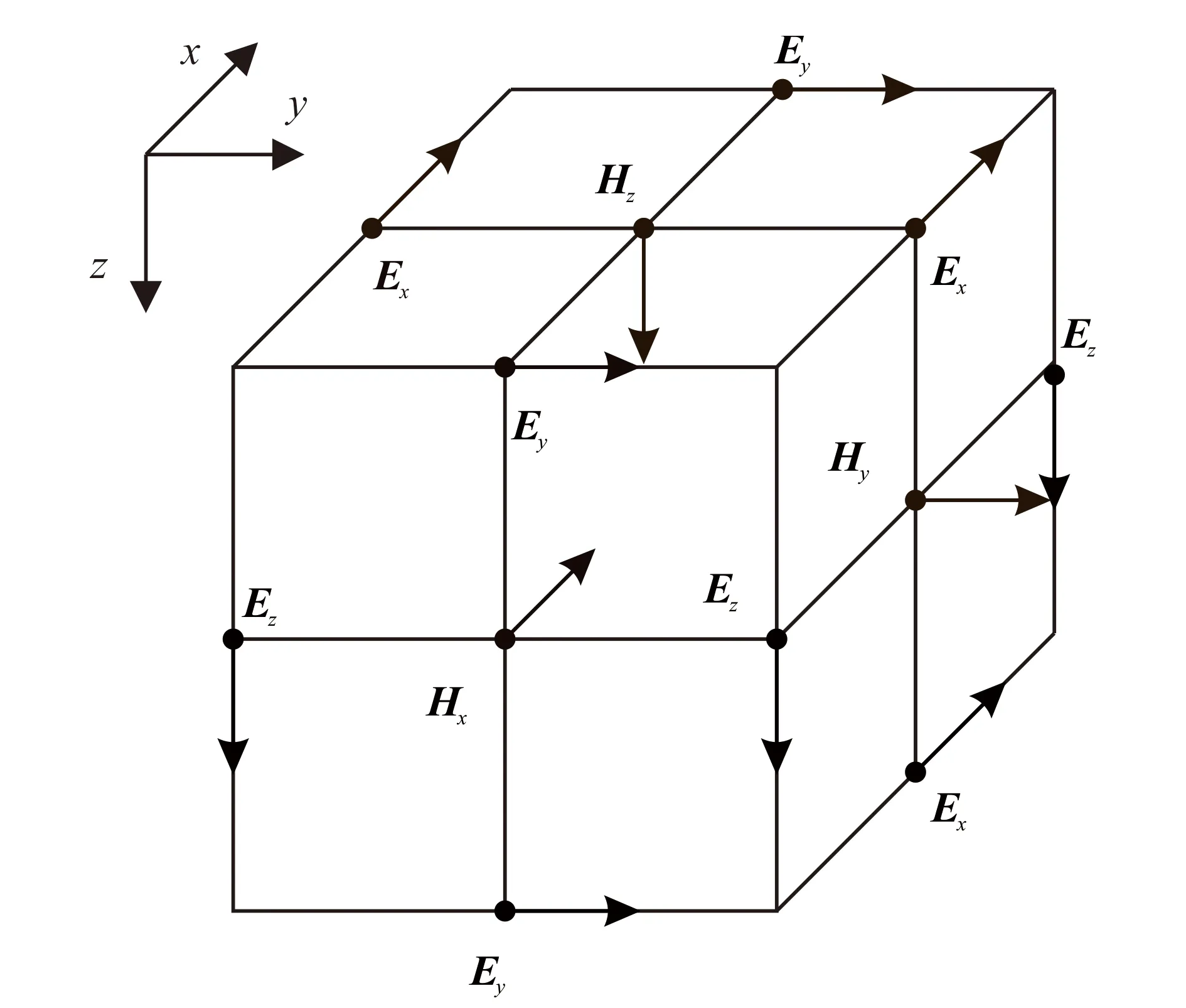
图1 三维有限差分模拟网格Fig.1 Three-dimension finite-difference grid
2 聚集多重网格算法
对线性方程组(2)的求解是大地电磁三维正演的关键之一。本文采用AGMG算法进行求解。该算法是一种新型的代数多重网格算法,通过基于矩阵图论思想的光滑聚集实现矩阵粗化,提高传统AMG算法的稳定性。该方法可分为聚集粗化以及迭代求解2个阶段。
2.1 聚集粗化
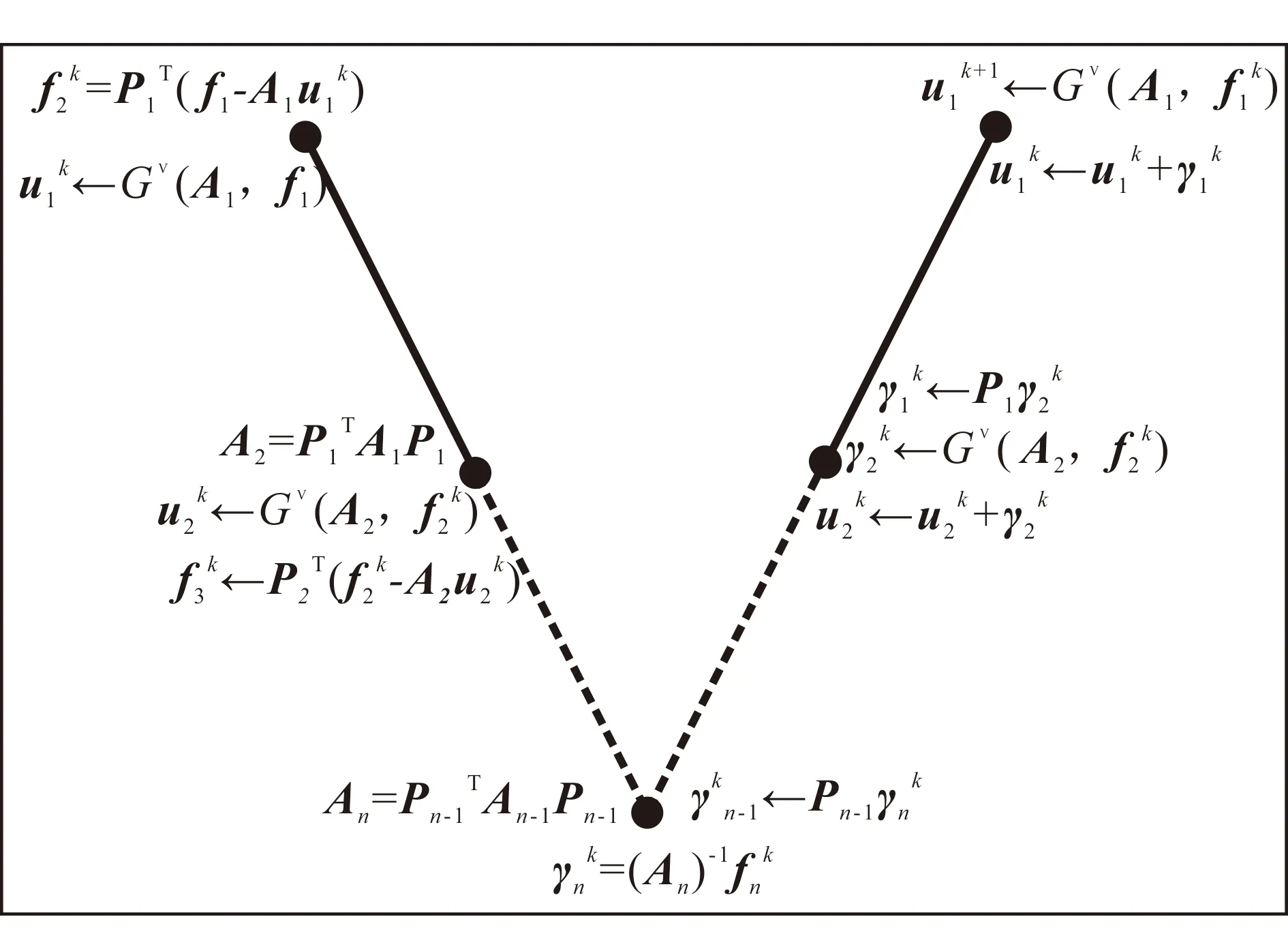
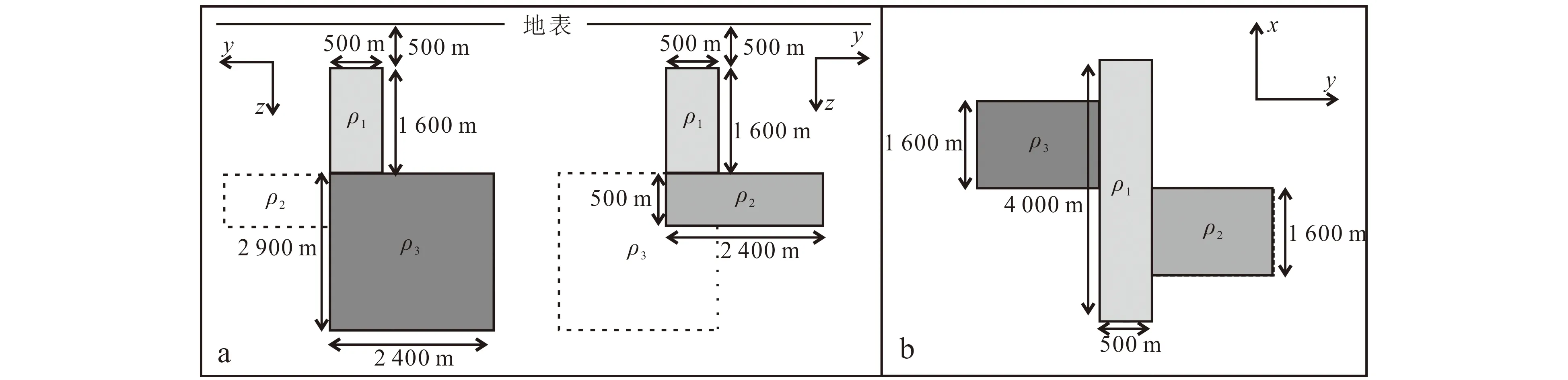
矩阵粗化是多重网格中最重要的部分。在几何多重网格中利用粗细网格之间的几何关系进行粗化。代数多重网格脱离了网格几何关系,可通过代数中的矩阵运算实现粗化。假设系数矩阵A,变量数为n,我们可以构建n×nc的延拓矩阵P,其中nc为粗化矩阵变量数。该矩阵能够将细网格上的变量集变换到粗网格变量集,实现矩阵粗化。粗化后系数矩阵Ac的变量数为nc(nc Ac=PTAP。 (3) 同时,我们定义延拓矩阵的转置为限制矩阵。 在AMG聚集粗化过程中,定义聚集变量集Gi(i=1,...,nc),它在几何意义上可认为是网格粗化后的网格节点;而在代数上Gi是矩阵粗化过程中的聚集变量集。Gi是系数矩阵A的互不相交子集,其大小等于粗化矩阵变量数nc。由此,延拓矩阵P定义为 (4) 式中:i表示矩阵A的变量序号;j表示聚集变量集Gj的序号。由(4)式可以看出延拓矩阵P为布尔矩阵,每行最多只有一个非零元素。将式(4)代入式(3)可得粗化矩阵Ac表达式为 (5) 式中,i、j分别表示粗化后的系数矩阵Ac行号和列号。 在AMG算法中,粗网格矩阵Ac的选取直接影响算法的稳定性和运行效率,因此延拓矩阵P的构建至关重要。本文采用Notay等[32]提出的成对聚集算法构建延拓矩阵P。该算法通过矩阵图论的正则覆盖,沿连通最好的方向进行聚集。对于任意一个系数矩阵A中的虚拟网格节点,通过寻找最强连通点进行配对并成对聚集。为此,首先定义虚拟节点i强连通点集为 (6) 式中,β为强弱连接阈值,需要根据系数矩阵A的特性进行选择。对于椭圆方程问题,β一般取0.25[32]。对于电磁问题,β一般取0.4~0.6。由此,聚集变量集Gi可写为 (7) 实际计算时,利用式(7)构建延拓矩阵P,再通过式(5)即可实现矩阵粗化。 在多重网格算法中,需要一定的套迭代技术将各层网格或矩阵连接起来。常用的套迭代技术循环方式有V循环、W循环、FMV循环。在实际应用中采用较多的是V或W循环。W循环能保持收敛因子不随网格而变化,具有Robust性,但耗费计算时间长;当网格层不多时,V循环具有与W循环相同的性质且计算量小。因此,本文采用V循环套迭代技术。 图2给出V循环套迭代技术流程图。V循环从细网格出发,逐渐粗化到最粗网格,最后又返回得到细网格上的解。图2中:PT表示把细网格上的残余误差限制到粗网格上的算子,称为限制算子;P表示把粗网格上的结果插值到细网格上的算子,称为插值算子;u为线性方程组迭代解;A表示某一层网格上的系数矩阵,而f表示针对该层网格线性方程组的右端项;Gv(A,f)表示光滑迭代;γ为粗网格修正量;k为迭代次数。由多重网格法的循环流程可以看出,迭代高频误差通过前光滑消去,而低频误差通过矩阵粗化转化为高频误差,在粗化矩阵上采用前光滑迭代消除;在最粗层上矩阵已经足够小,可采用直接求解算法进行求解。最后,通过限制算子逐层返回并进行后光滑处理消除残余误差,实现线性方程组的快速求解。对于光滑迭代Gv(A,f),采用Gauss- Seidel迭代法,迭代次数通常为1~3次,既能保持AGMG算法具有良好数值稳定性,又能很好地消除迭代过程中出现的高频误差。 图2 AGMG算法的V循环示意图Fig.2 V-cycle scheme in AGMG method 前人研究[33]表明,当系数矩阵A严重病态时,AMG算法中利用传统套迭代技术(V循环、W循环及FMV循环)难以取得好的效果,解容易发散。为此,通常将AMG算法与共轭梯度(CG)类算法相结合,将AMG算法用作共轭梯度类预处理算子,有效提高了传统AMG算法的计算速度和稳定性。本文设计2种求解策略求解线性方程组:传统的V循环AGMG算法(简称AGMG)及将AGMG作为传统Krylov子空间迭代算法的预处理算子。我们选用共轭梯度算法(CG)和广义共轭残差法(GCR)作为Krylov子空间迭代算法[34-35],分别简称为AGMG-CG和AGMG-GCR。 为检验本文实施3种聚集多重网格算法AGMG、AGMG-CG、AGMG-GCR的准确性和计算效率,我们参照2008年MT 3D Inversion Workshop提出的Dublin Test Model 1(DTM1)地电模型[36],设计一个典型的地电模型进行三维数值模拟,进而分别从计算速度、迭代次数、误差衰减特性及计算时间等方面进行分析,并与Kelbert等[37]开发的大地电磁三维正反演代码ModEM进行对比。本文所有算法均在Microsoft Visual Studio 2015开发平台上运行,采用Inter Visual Fortran 2016编译,程序运行环境为Interl(R) Core(TM) i7-6700HQ CPU @ 2.60 GHz四核八线程、16 G内存、64位win10系统。 为了验证本文算法精度,设计一个含有3个异常体的复杂地电模型。围岩电阻率为100 Ω·m;异常体ρ1为一个4 000 m×500 m×1 600 m的六面体,顶部埋深为500 m,电阻率为10 Ω·m;异常体ρ2为一个1 600 m×2 400 m×500 m的六面体,顶部埋深为2 100 m,电阻率为1 Ω·m;异常体ρ3为一个1 600 m×2 400 m×2 900 m的六面体,顶部埋深为2 100 m,电阻率为1 000 Ω·m。图3给出该模型在yz方向的剖面图和xy方向的平面图。在22.6 km×30.3 km×20.6 km的求解区域内,我们采用不等距进行网格剖分,剖分网格数为108×114×78。计算频率设为0.01 Hz,在求解区域正中心x方向上观测40个测点,间距为400 m。在完成x和y极化模式下的大地电磁场三维正演模拟后计算得到大地电磁阻抗。 图4为复杂地电模型不同求解算法的阻抗Zxy a.yz剖面图;b.xy平面图。图3 复杂地电模型示意图Fig.3 Sketch map of complex geoelectrical model 图4 不同求解算法的大地电磁三维正演结果对比Fig.4 Comparison of 3D MT numerical solutions for various iterative methods 和Zyx三维模拟结果对比。数值模拟分别采用本文实施的3种AGMG求解策略和Kelbert等[37]开发的大地电磁三维正演模拟程序ModEM求解,其中ModEM采用的迭代求解算法为QMR。由图4可见,本文采用的3种不同AGMG求解算法(AGMG、AGMG-CG和AGMG-GCR)与ModEM计算的阻抗Zxy和Zyx实、虚部吻合很好,验证了算法的准确性。 为了分析3种不同AGMG算法的计算效率,对图3中的模型设计4种不同规模的网格,分别为36×38×26、72×76×52、108×114×78、144×152×104,然后分别采用AGMG、AGMG-CG、AGMG-GCR和ModEM(QMR)对该模型进行x和y极化模式大地电磁三维正演模拟。求解区域为22.6 km×30.3 km×20.6 km,计算频率为0.01 Hz,求解相对误差设为10-8。 图5为x极化模式下不同迭代方法的误差衰减曲线对比图。其中,AGMG算法在网格大小为36×38×26时聚集粗化层数为6层,在72×76×52时聚集粗化层数为7层,在108×114×78时聚集粗化层数为8层,在144×152×104时聚集粗化层数为10层。从图5c中可以看出:传统QMR迭代算法在迭代早期呈现快速衰减,迭代误差衰减曲线光滑性较差,同时随着迭代次数增加衰减速度变慢;AGMG算法起始呈现快速衰减,随着迭代次数增加衰减速度变缓,但总体比QMR下降速度快,而且迭代误差衰减曲线较光滑;AGMG预处理的Krylov子空间迭代算法(AGMG-CG、AGMG-GCR)呈现近似线性下降特征,随着迭代次数增加衰减速度基本保持不变;另外,AGMG-GCR相对于AGMG-CG衰减速度更快,迭代误差曲线更光滑。综合对比不同网格尺度(图5a—d)的迭代衰减曲线可以看出,QMR和AGMG衰减速度随网格数增大衰减速度逐渐变慢,迭代次数随网格数增大急剧增加,而AGMG-GCR和AGMG-CG随网格数增大均保持近似线性快速下降,迭代次数随网格数增大增加较为缓慢,同时AGMG-GCR迭代速度优于AGMG-CG,迭代误差曲线更加光滑。 E. 最终迭代相对误差;NI. 迭代次数。a.36×38×26;b.72×76×52;c.108×114×78;d.144×152×104。图5 x极化模式不同求解算法的大地电磁三维正演误差衰减曲线Fig.5 Convergence behaviors of AGMG, AGMG-CG, AGMG-GCR and QMR for x-polarization 3D MT modelling with different grid sizes 图6为y极化模式下不同迭代方法的误差衰减曲线对比图,不同网格的聚集粗化层数与x极化模式相同。从图6中可以看出,4种方法的误差衰减曲线特征与x极化模式基本一致。AGMG-GCR相对于其他3种迭代算法,误差呈现近似线性下降,迭代次数随网格数增加较为缓慢,误差迭代曲线更光滑。因此,AGMG算法与传统Krylov子空间迭代算法结合,不仅能够改善AGMG的稳定性,而且能够加快收敛速度,而AGMG-GCR是一种更为快速稳定的迭代求解算法。 为了进一步对比AGMG算法的计算效率,本文对不同网格、不同迭代算法的迭代结果进行统计,结果见表1。从表1可以看出,4种迭代算法在不同网格数下均能满足设定的精度。在小尺度网格36×38×26时:QMR算法的迭代次数较多,迭代时间和正演模拟时间最少;AGMG-GCR迭代次数最少,迭代时间和正演模拟时间和QMR相当。随着网格尺度增加,4种迭代算法的求解时间和正演模拟时间急剧增加,这是由于网格尺度增加导致计算量增加的结果。但AGMG-GCR和AGMG-CG迭代次数增加缓慢,迭代时间和正演模拟时间增加的幅度远小于QMR和AGMG算法。在大尺度网格108×114×78时:QMR算法的迭代次数和求解时间均最大,而AGMG-GCR迭代次数和求解时间最小,相对于传统QMR算法加速了十几倍。综上所述,将AGMG算法作为传统Krylov子空间迭代法的预处理算子,在网格尺度较大时具有迭代次数少、计算速度快等优点,同时迭代误差呈近似线性下降,具有很好的稳定性。随着网格尺度规模增加,AGMG预处理算法迭代次数增加缓慢,加速效率变得越来越明显。特别地,AGMG-GCR是一种快速、稳定、高效的求解算法,为大规模问题的大地电磁三维模拟提供技术保障。 a.36×38×26;b.72×76×52;c.108×114×78;d.144×152×104。图6 y极化模式不同求解算法的大地电磁三维正演的误差衰减曲线Fig.6 Convergence behaviors of AGMG, AGMG-CG, AGMG-GCR and QMR for y-polarization 3D MT modelling with different grid sizes Table1Error,runningtimeinsecondsanditerationnumbersofAGMG,AGMG-CG,AGMG-GCRandQMRfor3DMTmodellingwithdifferentgridsizes 网格方法x极化y极化E/10-9NIts/sta/sE/10-9NIts/sta/s144×152×104AGMG10.006892704.26866.310.007903149.17954.7AGMG-CG14.00132638.91513.59.60154727.61726.9AGMG-GCR9.4088432.31044.09.6095459.71071.3QMR9.788695389.011207.79.9810176290.013069.4108×114×78AGMG9.90414920.41961.99.904671021.22164.3AGMG-CG10.0099284.6563.49.60102287.7562.1AGMG-GCR12.0066186.4397.89.4070190.1400.1QMR9.925321331.92898.69.957521803.73914.172×76×52AGMG10.00186234.4363.69.90242305.2486.6AGMG-CG9.806694.5140.79.5072102.1146.2AGMG-GCR10.004463.2107.110.005072.3116.5QMR9.47161121.2273.79.63239181.3391.136×38×26AGMG12.007719.331.31000.0010624.437.2AGMG-CG7.105312.520.19.305412.919.3AGMG-GCR9.70328.312.716.00338.514.4QMR9.60586.210.59.60778.313.3 注:ts. 迭代求解时间;ta. 包含散度校正的正演求解时间。 本文从准静态麦克斯韦方程出发,利用Yee氏交错网格有限体积法进行离散,并采用第一类Dirichlet边界条件得到关于待求解的电场线性方程组,然后引入新型多重网格算法——聚集多重网格算法进行求解,实施3种不同的多重网格求解算法(AGMG、AGMG-CG、AGMG-GCR)。通过典型三维地电模型的正演模拟,并与已有的ModEM正反演模拟软件对比验证了本文算法的准确性。同时,从数值模拟结果可得出如下结论: 1)在大地电磁法三维正演中,将传统AGMG算法作为Krylov子空间的迭代算法预处理算子,能够极大改善AGMG和Krylov子空间迭代算法的稳定性,加快误差衰减速度、减少迭代次数,有效提升正演求解效率。 2)AGMG-GCR算法具有随网格尺度增加迭代次数缓慢增加、误差呈近似线性下降的特征,是一种高效、快速、稳定的迭代求解算法,特别适合当前“精细化”和“大尺度”电磁正反演问题的求解。 致谢:本文验证程序为Kelbert等开发的大地电磁三维正反演代码ModEM,聚集代数多重网格理论是Yvan Notay等有关多重网格法的研究成果。感谢Anna等和Yvan Notay提供公开源代码及帮助的相关专家。 [1] Newman G A. A Review of High-Performance Com-putational Strategies for Modeling and Imaging of Electromagnetic Induction Data[J]. Surveys in Geophysics, 2014, 35(1): 85-100. [2] Smith R. Electromagnetic Induction Methods in Mi-ning Geophysics from 2008 to 2012[J]. Surveys in Geophysics, 2014, 35(1): 123-156. [3] Siripunvaraporn W. Three-Dimensional Magnetotellu-ric Inversion: An Introductory Guide for Developers and Users[J]. Surveys in Geophysics, 2012, 33(1): 5-27. [4] 谭捍东,余钦范,Booker John,等. 大地电磁法三维交错采样有限差分数值模拟[J]. 地球物理学报,2003,46(5):706-711. Tan Handong, Yu Qinfan, Booker J, et al. Magnetotelluric Three-Dimensional Modelling Using the Staggered-Grid Fnite Difference Method[J]. Chinese Journal of Geophysics, 2003, 46(5): 706-711. [5] 沈金松. 用交错网格有限差分法计算三维频率域电磁响应[J]. 地球物理学报,2003,46(2):281-289. Shen Jinsong. Modelling of 3-D Eectromagnetic Responses in Frequency Domain by Using Straggered-Grid Finite Difference Method[J]. Chinese Journal of Geophysics, 2003, 46(2): 281-289. [6] Mackie R L, Madden T R, Wannamaker P E. Three-Dimensional Magnetotelluric Modeling Using Difference Equations: Theory and Comparisons to Integral Equation Solutions[J]. Geophysics, 1993, 58(2): 215-226. [7] 李焱, 胡祥云, 杨文采, 等. 大地电磁三维交错网格有限差分数值模拟的并行计算研究[J]. 地球物理学报,2012,55(12):4036-4043. Li Yan, Hu Xiangyun, Yang Wencai, et al. A Study on Parallel Computation for 3D Magnetotelluric Modeling Using the Staggered-Grid Finite Difference Method[J]. Chinese Journal of Geophysics, 2012, 55(12): 4036-4043. [8] Haber E, Ascher U M. Fast Finite Volume Simulation of 3D Electromagnetic Problems with Highly Discontinuous Coefficients[J]. SIAM Journal on Scientific Computing, 2000, 22(6): 1943-1961. [9]Haber E, Ruthotto L. A Multiscale Finite Volume Method for Maxwell’s Equations at Low Frequencies[J]. Geophysical Journal International, 2014, 199(2): 1268-1277. [10] 陈辉,殷长春,邓居智. 基于Lorenz规范条件下磁矢势和标势耦合方程的频率域电磁法三维正演[J]. 地球物理学报,2016,59(8):3087-3097. Chen Hui, Yin Changchun, Deng Juzhi. A Finite-Volume Solution to 3D Frequency-Domain Electromagnetic Modelling Using Lorenz-Gauged Magnetic Vector and Scalar Potentials[J]. Chinese Journal of Geophysics, 2016, 59(8): 3087-3097. [11] Ren Z, Kalscheuer T, Greenhalgh S, et al. A Finite-Element-Based Domain-Decomposition Approach for Plane Wave 3D Electromagnetic Modeling[J]. Geophysics, 2014, 79(6): E255-E268. [12] 黄临平,戴世坤. 复杂条件下3D电磁场有限元计算方法[J]. 地球科学:中国地质大学学报,2002,27(6):775-779. Huang Linping, Dai Shikun. Finite Element Calculation Method of 3D Electromagnetic Field under Complex Condition[J]. Earth Science: Journal of China University of Geoscineces, 2002, 27(6): 775-779. [13] Mitsuhata Y, Uchida T. 3D Magnetotelluric Mode-ling Using the T-Omega Finite-Element Method[J]. Geophysics, 2004, 69(1): 108-119. [14] 李俊杰,严家斌,皇祥宇. 无单元Galerkin法大地电磁三维正演模拟[J]. 地质与勘探,2015,51(5):946-952. Li Junjie, Yan Jiabin, Huang Xiangyu. Three-Dimensional Forward Modeling of Magnetotellurics Using the Element-Free Galerkin Method[J]. Geology and Exploration, 2015, 51(5): 946-952. [15] 严家斌,皇祥宇. 大地电磁三维矢量有限元正演[J]. 吉林大学学报(地球科学版),2016,46(5):1538-1549. Yan Jiabin, Huang Xiangyu. 3D Forward Modeling of Magnetotelluric Field by Vector Finite Element Method[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(5): 1538-1549. [16]Kruglyakov M, Geraskin A, Kuvshinov A. Novel Accurate and Scalable 3-D MT Forward Solver Based on a Contracting Integral Equation Method[J]. Computers & Geosciences, 2016, 96: 208-217. [17]Wannamaker P E. Advances in Three-Dimensional Magnetotelluric Modeling Using Integral Equations[J]. Geophysics, 1991, 56(11): 1716-1728. [18] 王书明,李德山,胡浩. 三维/三维构造下大地电磁相位张量数值模拟[J]. 地球物理学报,2013,56(5):1745-1752. Wang Shuming, Li Deshan, Hu Hao. Numerical Modeling of Magnetotelluric Phase Tensor in the Context of 3D/3D Formation[J]. Chinese Journal of Geophysics, 2013, 56(5): 1745-1752. [19]de Groot-Hedlin C. Finite-Difference Modeling of Magnetotelluric Felds: Error Estimates for Uniform and Nonuniform Grids[J]. Geophysics, 2006, 71(3): G225-G233. [20] Han N, Nam M J, Kim H J, et al. A Comparison of Accuracy and Computation Time of Three-Dimensional Magnetotelluric Modelling Algorithms[J]. Journal of Geophysics and Engineering, 2009, 6(2): 136. [21] Smith J T. Conservative Mmodeling of 3-D Electro-magnetic Fields: Part II: Biconjugate Gradient Solution and an Accelerator[J]. Geophysics, 1996, 61(5): 1319-1324. [22] Siripunvaraporn W, Egbert G, Lenbury Y. Nume-rical Accuracy of Magnetotelluric Modelling: A Comparison of Finite Difference Approximations[J]. Earth Planets Space, 2002, 54: 721-725. [23]Mackie R L, Madden T R. Conjugate Direction Relaxation Solutions for 3-D Magnetotelluric Modeling[J]. Geophysics, 1993, 58(7): 1052-1057. [24] Weiss C J, Newman G A. Electromagnetic Induction in a Generalized 3D Anisotropic Earth: Part 2: The LIN Preconditioner[J]. Geophysics, 2003, 68(3): 922-930. [25] 陈辉,邓居智,谭捍东,等. 大地电磁三维交错网格有限差分数值模拟中的散度校正方法研究[J]. 地球物理学报,2011,54(6):1649-1659. Chen Hui, Deng Juzhi, Tan Handong, et al. Study on Divergence Correction Method in Three-Dimensional Magnetotelluric Modeling with Staggered-Grid Finite Fifference Method[J]. Chinese Journal Geophysics, 2011, 54(6): 1649-1659. [26]Streich R. 3D Finite-Difference Frequency-Domain Modeling of Controlled-Source Electromagnetic Data: Direct Solution and Optimization for High Accuracy[J]. Geophysics, 2009, 74(5): 95-105. [27] Puzyrev V, Koric S, Wilkin S. Evaluation of Parallel Direct Sparse Linear Solvers in Electromagnetic Geophysical Problems[J]. Computers & Geosciences, 2016, 89: 79-87. [28] Koldan J, Puzyrev V, de la Puente J, et al. Algebraic Multigrid Preconditioning Within Parallel Finite-Element Solvers for 3-D Electromagnetic Modelling Problems in Geophysics[J]. Geophysical Journal International, 2014, 197(3): 1442-1458. [29] Mulder W A. Geophysical Modelling of 3D Electro-magnetic Diffusion with Multigrid[J]. Computing and Visualization in Science, 2008, 11(3): 129-138. [30]Pan K, Tang J. 2.5-D and 3-D DC Resistivity Modelling Using an Extrapolation Cascadic Multigrid Method[J]. Geophysical Journal International, 2014, 197(3): 1459-1470. [31]Trottenberg U, Clees T. Multigrid Software for Industrial Applications: From MG00 to SAMG[M]. Heidelberg: Springer, 2009: 423-436. [32] Notay Y. An Aggregation-Based Algebraic Multigrid Method[J]. Electronic Transactions on Numerical Analysis, 2010, 37(6): 123-146. [33] Henson V E, Yang U M. Boomer AMG: A Parallel Algebraic Multigrid Solver and Preconditioner[J]. Applied Numerical Mathematics, 2002, 41(1): 155-177. [34] Saad Y. Iterative Methods for Sparse Linear Systems[M]. Philadelphia: SIAM, 2003. [35] Pflaum C. A Multigrid Conjugate Gradient Method[J]. Applied Numerical Mathematics, 2008, 58: 1803-1817. [36]MT 3D Inversion Workshop. Dublin Test Model 1 (DTM1)[EB/OL]. [2016-10-20] http://www.complete-mt-solutions.com/mtnet/workshops/mt3di-nv/ 2008_Dublin/Dublin/3dmodel.html. [37] Kelbert A, Meqbel N, Egbert G D, et al. ModEM: A Modular System for Inversion of Electromagnetic Geophysical Data[J]. Computers & Geosciences, 2014, 66: 40-53.2.2 迭代求解
3 模型算例
3.1 精度验证
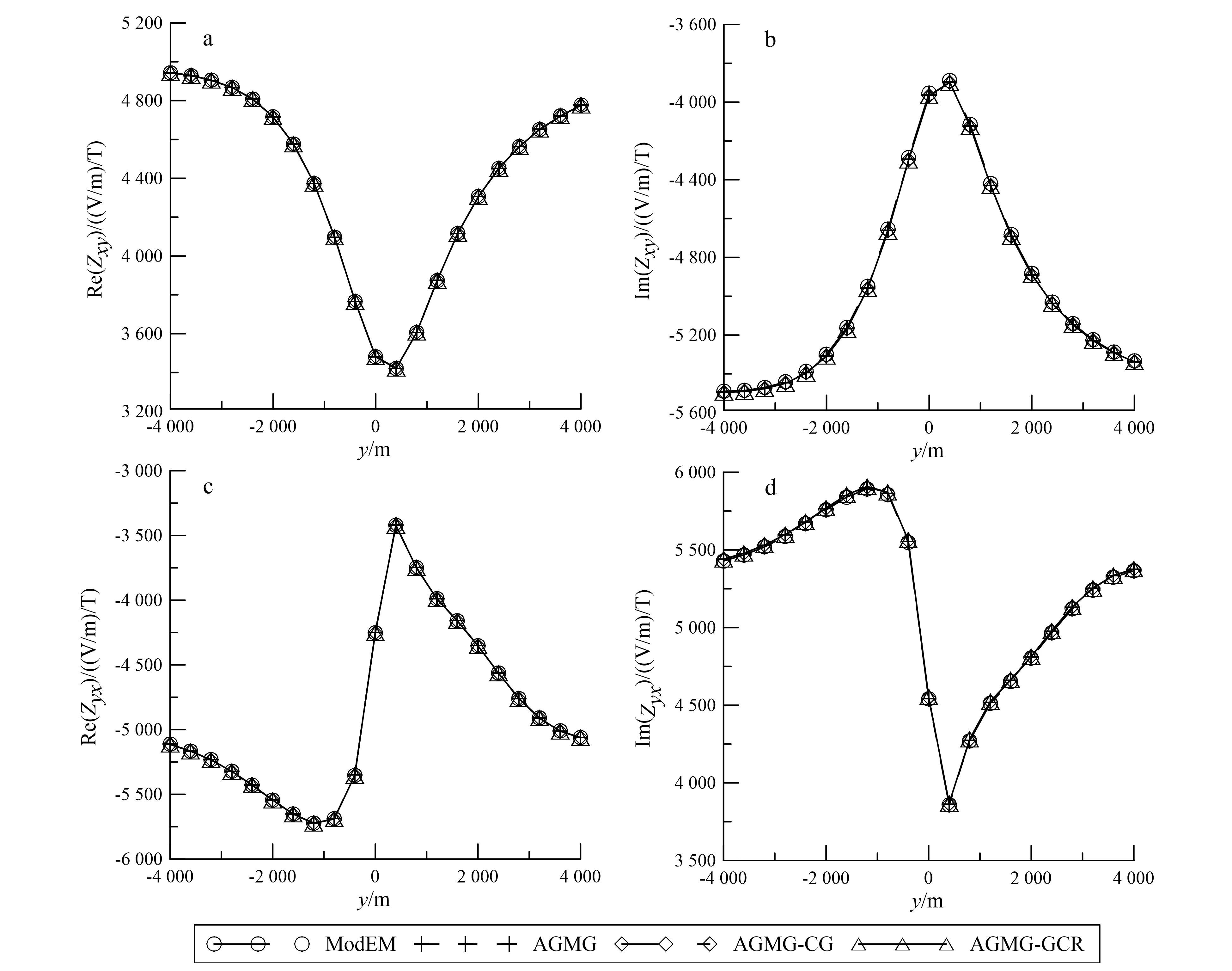
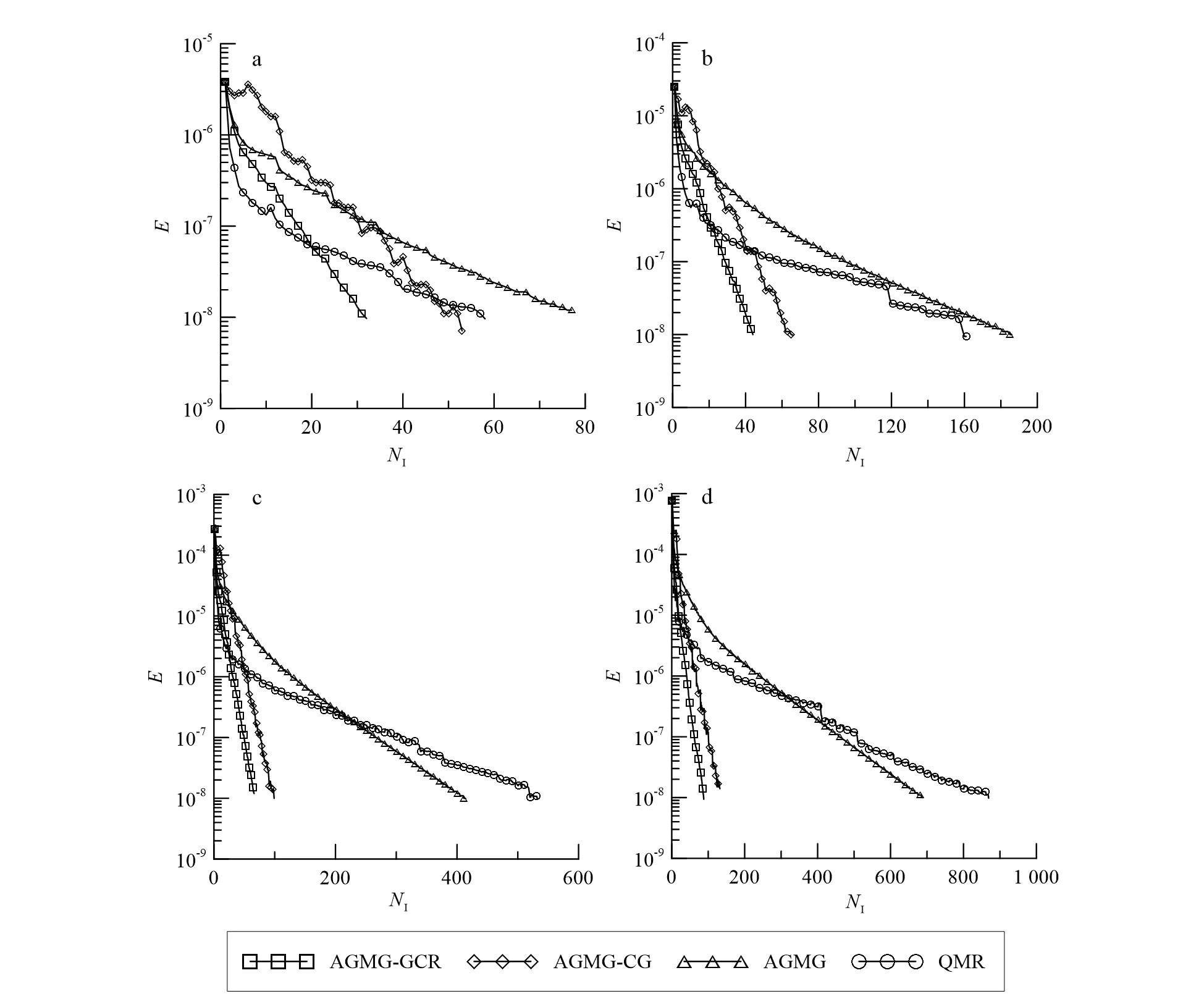
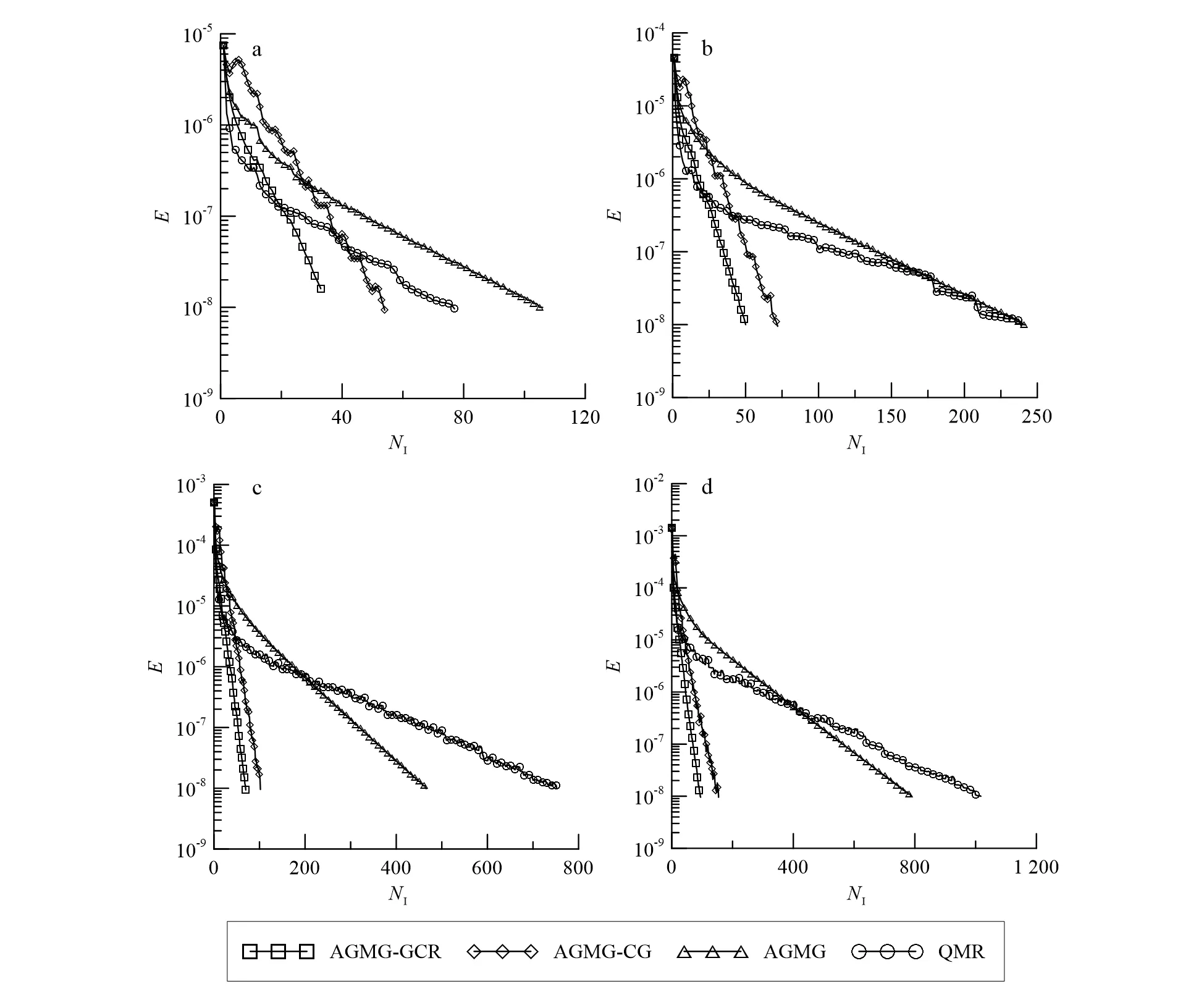
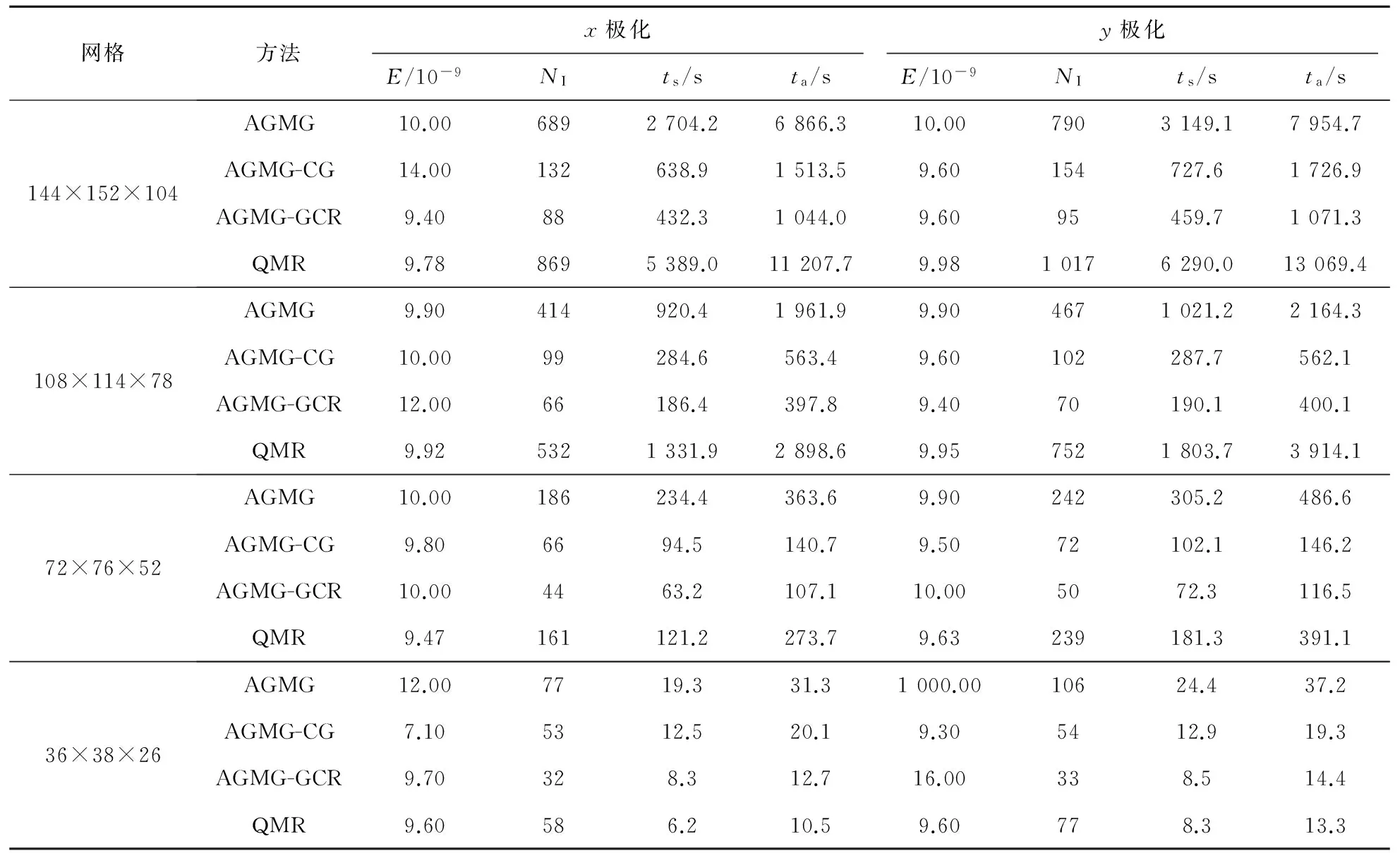
3.2 AGMG算法效率分析
4 结论与建议
