基于双版面Hotelling模型的在线广告灵活版面定价策略研究
2018-01-25许淑君
许淑君
(上海财经大学国际工商管理学院,上海 200433)
1 引言
随着互联网用户的飞速发展,在线广告大量涌现。在线广告符合时间碎片化、使用便捷化等特点,更便于按需分类推送和与用户交互[1],因此其转换率更高。2014年中国在线广告市场规模1540亿元,同比增长达到40.0%[2]。而美国2015年仅上半年的在线广告收入就增长了19%,已连续21个季度保持收入两位数的年增长率[3]。
在线广告是广告版面供应方提供给版面需求方,供其利用邮件、搜索引擎、社交媒体等形式将营销讯息传递给网页浏览者的广告形式。浏览者是广告版面需求方力图吸引的潜在消费者[4]。在线广告大致分为赞助搜索广告和展示广告两类[5]。赞助搜索广告是指广告版面需求方将广告置于对特殊搜索词的检索结果旁,诸如Google和Yahoo的搜索引擎[6]。而展示广告则是网页版面商,如Yahoo和MSN,通过提供网页版面位置给需求方,配合其在网站上刊登广告从而获取收入。本文将研究专注于在线展示广告(以下简称在线广告)最大化收益的定价问题。
有关在线广告管理的研究最初焦距在网络平台方定价方面,Karmarkar等[4]为建立了基于PPV(Price-per-view)和PPC(price-per-click)计费方式的收益管理模型,其他还有关于展示计费模式[7]、点击率收费定价[8-9]、实时竞价(Real-Time Bidding, RTB)与拍卖[10-11]、版面设计分布与定价模式等的研究[12-13]、空间优化与配置等[14-16]。Akcay等[17]研究了多个易逝品的联合定价问题。还有些学者们关注需求不确定性,基于时序研究排队问题[18-19]、广告排期问题等[20]。后来有关在线广告的研究将重点转向了版面库存问题上,运用动态价格模型[21]、启发式算法[14]、或基因算法等[13]进行研究。更多的此类研究参见Talluri等的综述[22]。而Sandeep等的研究表明,因网络平台面临巨大需求不确定和库存不确定[18],收益管理方法将比空间分配方法增加16-20%的收益,更比先到先服务等排队策略增加80%收益[4]。在线广告容量的易逝性决定了对其进行收益管理研究的意义远大于库存管理。广告位零库存也不一定能够实现收益最大化。收益最大化才是版面供应方的目标所在。
收益管理(Revenue Management 或 Yield Management)是根据不同的需求特征(如偏好)通过歧视性定价(price discrimination),最大限度开发市场潜在需求而谋求收益最大化的新型管理技术[17]。实践中的收益管理策略有模糊产品、概率性销售、产品升级等[23]。有关收益管理研究可以说汗牛充栋,一部分研究从随机容量控制或价格制定方面进行建模求解,如Brtran和Caldentey[24],还有的研究在价格制定中考虑了消费者行为,如宋鸿芳等[25]的研究考虑了消费者受参考价格的锚定效应,陈章跃等[26]的研究考虑了需求方策略性行为。
灵活产品就是收益管理的主要策略之一[27]。“灵活产品”概念2004年一经Gallego等人提出就很快被扩展到在线广告领域[28]。目前,国内外有关灵活产品的研究主要集中在定价策略[29]、概率性销售[30]、服务透明性[31]等方面。基于灵活产品(flexible product)的定义,本文定义“灵活版面”为:服务于相同市场的两个或两个以上版面的虚拟组合,旨在提高版面的利用率和引导需求,从而提高供应方收益。供应方在预定结束时根据预定结果和需求信息,有权将该虚拟组合中的任一版面分配给灵活版面预定者,解决供需错配问题以提高收益[32]。Gallego等[27]用两阶段的定价模型验证了灵活产品规避风险与引导需求的作用,同时发现实践中灵活产品策略不一定增加供应方收益,灵活产品策略的关键在于确定产品和灵活产品的协调定价。Fay等[30]的研究仅限于“可能产品(Probabilistic goods)”与传统销售的比较,其重点在于对可能产品的益处。但这些研究都未能回答在线广告的如下问题:确定版面与灵活版面价格要如何协调方能使供应方收益最大化?灵活版面是否会导致供应方跌落降价陷阱从而使得其反?需求方是否会选择灵活版面及何时选择选择灵活版面?版面容量大小及需求方的版面偏好又将如何影响灵活版面策略的效果?
为此,本文顺应在线广告整售模式的发展,贴近企业实践而采用一阶段定价模式,再考虑到在线广告版面内容差异性和版面间的可替代性,建立一个基于需求方偏好的双版面Hotelling模型,深入分析版面需求方在不同价格区域的策略性行为,探求供应方利用灵活版面策略最大化收益的策略区间,并以此找到确定版面与灵活版面的最优价格组合策略。
2 问题描述与参数假设
在线广告行业具有客户需求不确定、购买间接性等特性,广告版面需求方往往基于购买时间、产品属性和价格做出购买决策[33]。在线广告版面供应方则提前预售,给版面偏好客户以相对高价,给价格敏感者的客户以折扣价[19],从而寻求收益最大化。因此,本文假设在线广告版面供应方基于需求方在版面上的偏好差异性和价格敏感性进行预售,其预售与分配时间轴如图1所示。

图1 版面预订及分配过程
广告版面供应方在预订开始就确定版面A和B的确定版面价格P及灵活版面价格PF。灵活版面比确定版面的价格低,即PF 为便于建模,本文特作如下假设: 假设1: 两种特定主题的版面,如娱乐版面和财经版面,因其主题属性不同而吸引不同消费群体。现实中,不同主题版面的价格往往相差无几。娱乐版面受众广,而财经版面转换率高。为简化模型,这里假设版面A和版面B的价格相同,即PA=PB=P。因在线广告增售一单位版面的边际成本非常低,版面供应方从不闲置广告版面[34]。故假设每单位广告版面销售成本为0。 假设2: 两种版面的容量相同,即CA=CB=C。本文将市场需求以“1”为单位进行标准化,则相对应的市场供给,即版面容量C也同时标准化。供应方可提供的版面总容量为2C。 Hotelling模型旨在基于空间差异讨论两个寡头间的价格竞争均衡问题。这种“空间差异性”可以是消费者距离商家的地理位置,也可表现为需求方的偏好差异性[31]。本文中将其确定为在线广告版面需求方对两个不同主题广告版面的偏好差异。假设广告版面需求方对两个版面的偏好均匀地分布在一条单位线段上。这条单位线段的左右各端点分别是版面A和版面B(如图2所示)。假定每一个需求方最多只购买一单位的广告版面。需求方基于对版面偏好不同而形成的分布位置记为x。Vj(x)代表版面j对每个在单位线段上位置为x的需求方的价值。假设需求方对理想版面的价值判断被标准化为1。需求方对两个不同版面的偏好效用敏感度记作t,其中0 图2 Hotelling双版面模型 在单位线段上位置为x的需求方对两端的版面A和B的价值判断分别是: (1) 其中,x~∪[0,1] 假设3: 假设需求方在预订期内具有完美信息。因灵活版面价格较低,其需求量大于或等于其供应量的假设,因此需求方最终可能以灵活版面价格获得版面的概率为ξ,且0ξ1。当ξ<1时意味着灵活版面超售。当确认获得版面后,需求方会以φ的概率被分配到版面A,以(1-φ)的概率被分配到版面B,其中0φ1。且假设ξ,φ皆为内生。则需求方对灵活版面F的预期价值判断为: VF(x)=φVA(x)+(1-φ)VB(x) (2) (3) x1代表购买版面A或以一定概率获得灵活版面F的消费者剩余(Consumer Surplus, CS)相等的临界点;x2代表购买版面B或以一定概率获得灵活版面F的CS相同临界点。 VA(x1)-P=[VF(x1)-PF]·ξ (4) VB(x2)-P=[VF(x2)-PF]·ξ (5) (6) 由式(4)、式(5)与式(6)得到: 因而,在满足模型成立条件的基础上,模型求解的问题可以转化为求解方程: (7) 求解条件如下: (1)灵活版面的存在,表明确定版面A和版面B的实际销售量不超过两种版面各自的容量,因此x1≤C,x2≤C; 联立求解条件得到如下约束条件: (8) 灵活版面策略使用的前提是在线广告需求不确定性,当广告版面供应方以价格P接受确定预定时,版面需求方对于确定版面A或B的需求Dj(j∈{A,B})小于其供应: (9) (10) 此时,采用灵活版面策略引导版面市场需求。此时确定版面与灵活版面的总需求大于等于总容量,所以C满足: 0 (11) 由式(10)、式(11)可知, (12) 广告版面需求方在MD区域的策略行为兼顾各自偏好和最大化CS的目标进行。研究发现这个区域的需求方策略在灵活版面三个价格区间中各不相同。 图3 当时,模型的均衡解示意 证明:当2t(1-P-2C+Ct+2CPF)≤0时, 总之,广告版面需求方做出策略性选择:是接受较高价格的确定版面,还是以低价接受可能任何版面都得不到的风险,这不仅取决于需求方自身的偏好强弱,而且取决于在灵活版面F不同价格下的CS: 在明确需求方在MD区域的策略行为后,下面分析广告版面供应方的收益情况。由式(9)可以依价格分为三个区域:高价格需求区HD、中价格需求区MD和低价格需求区LD。依上述灵活版面价格的分析,又可以将MD区域再分为灵活版面低价格区域MDLF、灵活版面高价格区域MDHF和无灵活版面价格区域MDNF。 在MDLF区域,因PF定价过低,诱使所有需求方都放弃偏好而选择灵活版面,此时广告版面供应方的收益为RMDLF=2CPF。显然,收益将随着PF的增大而增大。同时考虑该区域PF与P的取值范围,故在点U处得到收益极大值: 在MDHF区域,偏好强的需求方选择确定版面,而偏好弱的需求方选择灵活版面,其收益为两种版面之和: 推论1:用反证法可证明确定版面的预定量随灵活版面价格单调增加。 结合推论1与定理4,供应方收益极大值发生在图5的G点处。 根据定理5及条件PF≤P,MDNF区域收益极大值发生在图5中的Q点处。 以上结果综述见表1与图5所示。 表1 供应方不同定价策略下的收益分析 由表1,HDLF区域、LDNF区域和MDLF区域的收益极大值相等,且都小于MDHF区域的极大值收益,因而不是供应方最佳策略行为区域。HDLF、LDNF和MDLF价格组合区域本质就是降价促销。 图5是由确定版面价格和灵活版面价格形成的两维空间中不同价格区域的收益变化以及其极大值所在。图中箭头方向为该区域收益增大方向。 图5 供应方收益及策略行为分析 图6 MDHF与MDNF的收益随市场容量C与偏好比较 本文研究在线广告整售模式下,广告版面供应方应对版面易逝性和版面需求不确定性的灵活版面策略定价问题。基于在线广告版面间的可替代性和易逝性特征,建立了整售模式下完美信息双版面Hotelling模型,在确定版面价格与灵活版面价格的不同组合区域内,分析广告需求方基于偏好特性与消费者剩余的策略选择行为,发现了供应方灵活版面最后定价空间。通过以上研究,得到的主要结论如下: 1)灵活版面策略只有在确定版面与灵活版面协调定价下才能有效提高版面供应方的收益。灵活版面的定价不能太低,否则将因需求方放弃偏好而致使供应方跌落降价陷阱。这都会降低供应方收益。 2)在确定版面与灵活版面不同定价组合下,收益的变化比较复杂。在LD区域,收益将随着确定版面价格的增加而增加;在MDLF区域和HDLF区域,供应方收益将随着灵活版面的价格上升而上升;在MDNF区域,收益将随着确定版面价格的下降而上升。 3)当广告版面的总容量足够大时,制定适中的确定版面价格,那么灵活版面策略可使供应方收益达到最大值。最大值将随着需求方的偏好效用敏感度单调增加。而当广告版面的总容量不是很大时,若需求方的偏好效用敏感度大,则灵活版面策略仍然能够提高供应方的收益。 4)灵活版面策略的适用条件:一是需要广告版面容量C足够大,二是需求方偏好效用敏感度t足够大。如果版面容量太小,没有必要采用灵活版面策略。 总之,灵活版面策略的使用需要确定版面与灵活版面价格之间协调进行。 本文仅考虑了两个不同版面之间的替代性,关注两者间不同定价组合情形下灵活版面的定价策略,且假定两个版面的价格同步相等、灵活版面的需求大于其供应。事实上,灵活版面在两个以上版面之间的应用更为复杂和灵活,而确定版面的不同定价必将影响灵活版面定价策略,灵活版面的需求不一定大于供应。在后续研究中,将考虑松弛这些假设,将版面数向两个以上的版面拓展,并考虑确定版面定价不同纳入考虑范围。 [1] 温冬开. 美国网络广告效果研究述要[J].广告大观(综合版), 2001,(2):32-33. [2] 艾瑞咨询.2014年中国网络广告行业年度监测报告[R].[2014-04-14].http://www.iresearch.com.cn/report/2138.html. [3] 中文互联网数据资讯中心.IAB:2015年上半年美国广告收入调查报告[R].[2015-11-19].www.1991it.com/archives/399344.html. [4] Karmarkar S, Dutta G.Multi-period revenue management model for Internet advertising [J]. Journal of Revenue & Pricing Management, 2012:(1-15). [5] Roels G, Fridgeirsdottir K.Dynamic revenue management for online display advertising [J]. Journal of Revenue and Pricing Management, 2009, 8(5): 452-466. [6] Feng Juan, Bhargava H K, Pennock D M. Implementing sponsored search in web search engines: Computational evaluation of alternative mechanisms [J]. Social Science Electronic Publishing, 2007,19(1):137-148. [7] Amiri A, Menon S. Scheduling banner advertisements on the web [J]. Informs Journal on Computing 2004, 16(1): 95-105. [8] Chickering D M, Hecherman D. Targeted advertising on the wet with inventory management [J]. Interfaces, 2003, 33(5): 71-77. [9] Chatterjee P, Hoffman D, Novak T P, Modeling the clickstream: implications for web-based advertising efforts [J]. Working paper, Rutgers University,1998. [10] 朱丽辉. 在线广告中实时竞价机制研究与算法实现[D]. 上海:华东师范大学. 2015. [11] 卜天明. 网络经济若干拍卖机制的研究[D]. 上海:复旦大学,2007. [12] Kumar S, Jacob V S, Sriskandarajah C, Scheduling advertisements on a web page to maximize revenue [J]. European Journal of Operational Research. 2006,17(3):1067-1089. [13] 刘佳曦. 美国三大门户网站网络广告特征研究[D]. 长春:东北师范大学. 2009. [14] Talluri K T, van Ryzin G J.The theory and practice of revenue management [M]. New York. Springer Science + Business Media, Inc., 2004. [15] Aggarwal C C, Wolf J L, Yu P S.A framework for the optimizing of www advertising [M]//Lamersdorf W,Merz M.Trends in distributed systems for electronic commerce.Berlin,Heidelberg:Springer,1998. [16] Dawande M,Kumar S, Sriskandarajah C. Performance bounds of algorithms for scheduling advertisements on a Web page [J], Journal of Scheduling, 2003, 6(4):373-394. [17] Akcay Y, Natarajan, H P, Xu S H.Joint dynamic pricing of multiple perishable products under consumer choice [J].Management Science. 2010, 56(8):1345-1361. [18] Araman V F, Fridgeirsdottir K. Online advertising: Revenue management approach [J]. Working Paper, London Business School,2008. [19] Fridgeirsdottir K, NajafiAsadolahi S. Revenue management for online advertising: Impatient advertisers [J]. Working Paper,London Business School. 2008. [20] Turner J, Scheller-Wolf A A. Tayur S R. Scheduling of dynamic in-game advertising [J].Working Paper, Carnegie Mellon,2008. [21] Gallego G, van Rzin G J, Optimal dynamic pricing of inventories with stochastic demand over finite horizons [J]. Management Science. 1994, 40(8):999-1020. [22] Adler M, Gibbons P B, Matias Y, Scheduling space-sharing for internet advertising [J]. Journal of Scheduling. 2002,5(2):103-119. [23] Gallego G, Stefanescu C. Upgrades, upsells and pricing in revenue management [J]. Working Paper, London Business School,2007. [24] Bitran G, Caldentey, R. An overview of pricing models for revenue management [J].Manufacturing & Service Operations Management. 2003, 5(3):203-229. [25] 宋鸿芳,冉伦,褚宏睿,等.消费者锚定效应下的动态定价与库存问题[J]. 中国管理科学,2015,23(4):123-128. [26] 陈章跃,王勇,刘华明. 考虑顾客策略行为和产品质量的闭环供应链决策模型[J]. 中国管理科学,2016,24(3):109-116. [27] Gallego G, Phillips R.Revenue management of flexible products [J]. Manufacturing & Service Operations Management, 2004: 321-337. [28] Gallego G, Iyengar G, Phillips R, et al, CORC technical report TR-2004-01 managing flexible products on a network [R]. Working paper,Colimbia University,2004. [29] Post D. Variable opaque products in the airline industry: A tool to fill the gaps and increase revenues [J]. Journal of Revenue and Pricing Management, 2010,9(4): 292-299. [30] Fay S, Xie Jinhong. Probabilistic goods: A creative way of selling products and services [J]. Marketing Science, 2008, 27(4):674-690. [31] Gallego G, Stefanescu C.Service engineering: The future of service feature design and pricing[R].Working Paper,Columbia University. 2011. [32] Müller-Bungart M. Revenue management with flexible products: models and methods for the boarding industry[M].Berlin-Heidelbeng:Springer. 2010. [33] Gallego G, Hu Ming.Dynamic pricing of perishable assets under competition [J]. Social Science Electronic Publishing, 2013, 60(5): 1241-1259. [34] 王国才, 朱道立. 基于收益管理的广告业时段最优分配模型[J].预测, 2004, 23( 3): 50-53. [35] 周蓉, 杨佩芝. 传媒产业收入管理特征和发展前景研究[J]. 上海管理科学, 2009,(31): 18-22.3 模型建立及求解




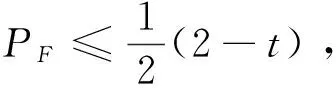


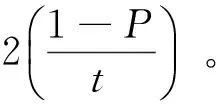
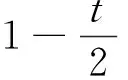

4 广告版面需求方在MD区域的策略性行为分析










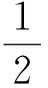
5 广告版面供应方基于收益最大化的定价策略分析
5.1 版面供应方基于需求方策略行为的收益比较


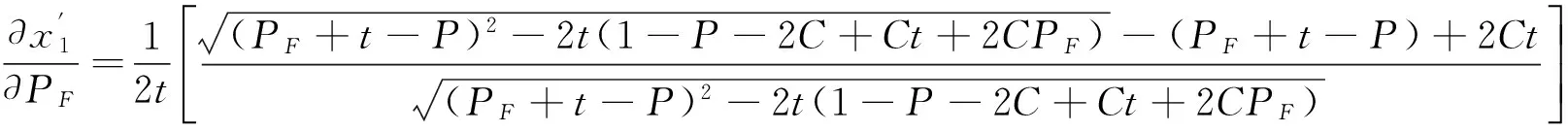
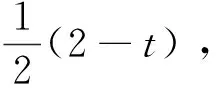
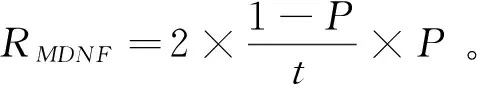
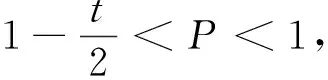

5.2 供应方不同组合价格下收益变化分析

5.3 不同版面容量下供应方最大收益的变化
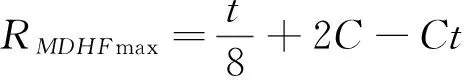

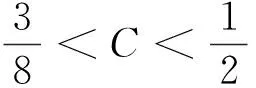

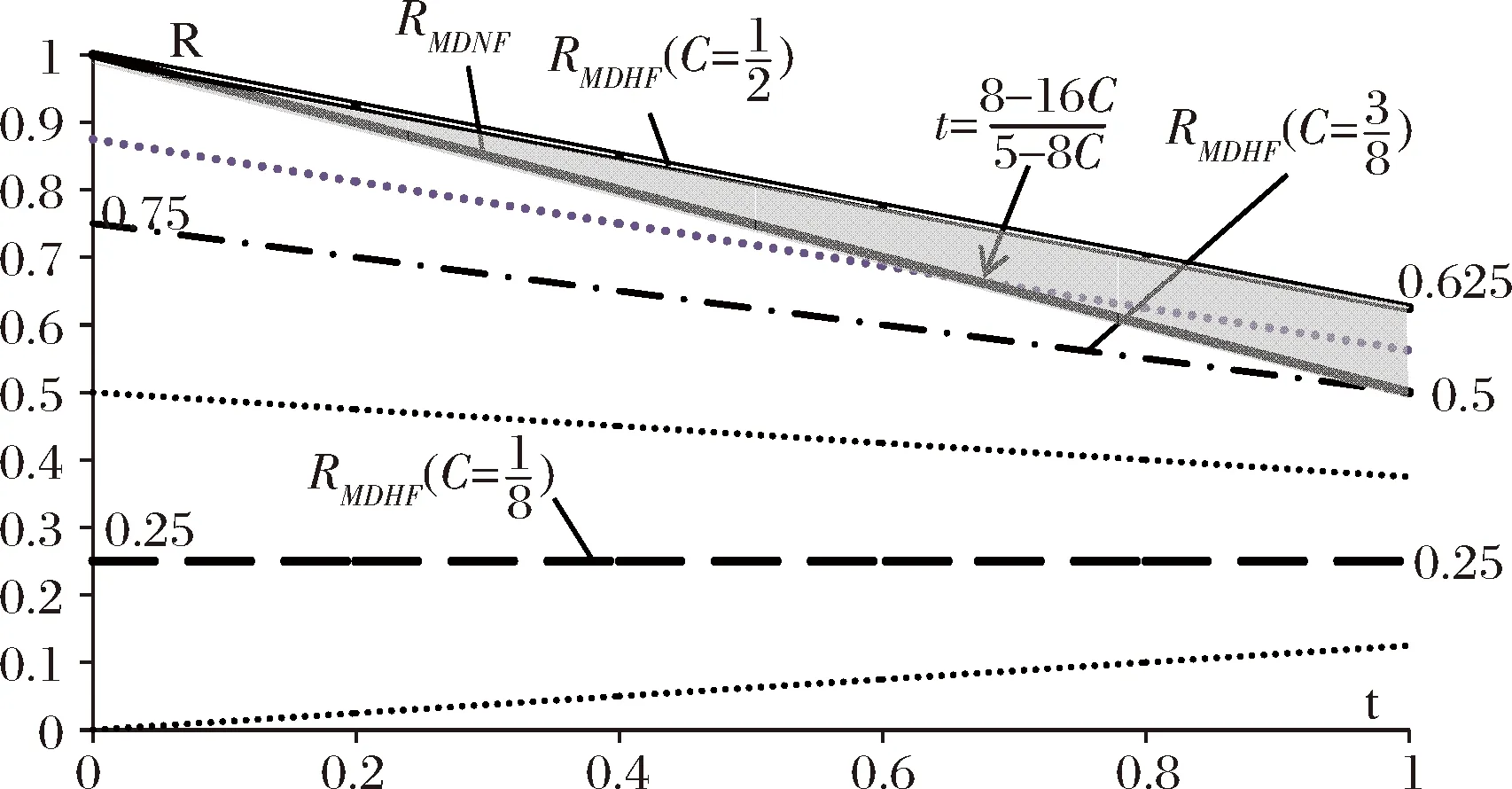
5.4 需求方偏好效用敏感度对供应方收益的影响
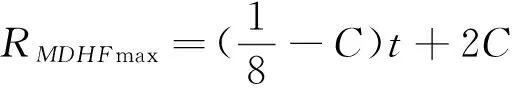
6 结语
