尾风险度量与定价能力分析
2018-01-25邢红卫刘维奇王汉瑛
邢红卫,刘维奇,2,王汉瑛
1 山西大学 管理与决策研究所,太原 030006 2 山西财经大学 财政与金融学院,太原 030006 3 山西财经大学 会计学院,太原 030006
引言
经典的资本资产定价模型假设资产收益服从正态分布或者投资者效用函数是二次型,因而在均值-方差偏好下分析收益与风险的关系。然而,实际中资产收益的分布却具有尖峰厚尾特征,或者说极端收益出现的概率远高于正态分布尾部所表明的[1-3],因此均值-方差框架下的方差风险并不能完全刻画资产价格极端变化所产生的尾风险。实证结果也表明,在资产价格存在极端变化的前提下,平均50%以上的已实现方差风险溢价都归结于尾风险[4-5]。实际中,资产价格的大幅变化基本都呈现缓涨暴跌的模式[6]。依据前景理论,与资产价格正的极端变化相比,投资者更关心资产价格负的极端变化带来的风险,因而尾风险又被称为左尾风险、极端下行风险、崩盘风险或灾难风险。RIETZ[7]和BARRO[8]发现负的极端收益可以有效解释股权溢价之谜,因此尾风险可能是潜在的风险定价因子。基于此,本研究探讨尾风险是否具有定价能力,这将有助于进一步理解金融系统性风险的内涵。
1 相关研究评述
基于理性定价理论,高风险应该预期高收益,因此尾风险应该有正的风险溢价。然而,从行为金融学的角度分析,高的尾风险会使投资者产生恐慌情绪[4-5],进而增加风险厌恶程度,看空市场前景,抛售现有资产或减少未来投资。在卖空限制下,由均衡定价理论可知资产未来价格会进一步降低,因而尾风险与股票预期收益是负向关系,即尾风险应具有负的风险溢价。目前,关于尾风险溢价的实证研究尚未得到一致结论。HUANG et al.[9]、KELLY et al.[10]和陈国进等[11]以基于Fama-French的3因子(FF3)或基于FF-Carhart的4因子模型的股票收益残差度量尾风险,发现尾风险载荷高的股票有高的预期收益。然而VAN OORDT et al.[12]同样以个股收益提取尾风险,发现尾风险高的股票有低的预期收益,这种现象在市场下跌期尤为显著,而在其他时期尾风险溢价并不稳健;MITTON et al.[13]、BOYER et al.[14]和郑振龙等[15]发现特质偏度与股票预期收益之间存在负向关系,由于特质偏度与尾风险之间的相关性,因而这些研究也在一定程度上表明尾风险对股票收益有负向预测能力。
如何度量尾风险是分析其收益预测能力的关键,目前尾风险的度量方法大致可分为3类。第1类是基于股票收益的高阶矩,如偏度和峰度[16-17]。BARNDORFF-NIELSEN et al.[18]和JACOD[19]的研究结果表明,已实现收益的3阶矩依概率收敛于收益跳跃强度的3次方,因此AMAYA et al.[17]将已实现收益的偏度作为尾风险的代理指标。然而,CREMERS et al.[20]的实证研究表明尾风险与已实现收益的偏度有较低的相关性,已实现偏度并不能作为尾风险的代理变量;BAI et al.[21]发现峰度对股票收益的预测能力可以被波动率和偏度完全解释,因而峰度也不能作为尾风险的代理指标。第2类是基于股票收益超过阈值的条件方差或与市场收益的条件协方差。ANG et al.[22]以低于平均市场超额收益的个股超额收益与市场超额收益的条件协方差计算贝塔,作为股票下行风险的度量指标;BALI et al.[23]假设收益服从HANSEN[24]提出的有偏t分布,以低于尾部分位点收益的方差作为尾风险的代理指标。但ANG et al.[22]和BALI et al.[23]都没有区分正常收益与极端收益对尾风险的不同影响,而且在方差和协方差计算中变量是以等权形式进入,也没有考虑不同程度的极端收益对尾风险的不同影响。第3类基于极值理论,以极值分布的极值指数作为尾风险的代理指标[10-12]。极值指数描述了分布尾部收敛于0的速率,极值指数越大,分布尾部收敛于0的速率越慢,收益极端变化的频率和幅度越大,表明尾风险越大。因而,极值指数可以作为合理的尾风险度量指标,目前估计极值指数的方法主要有超越阈值(peak over threshold,POT)方法和块最大(block maxima,BM)方法。
在基于极值理论的尾风险度量方面,BALI et al.[23]混合美国股票市场所有股票在每个月的日收益形成月度数据池,以5%分位点作为厚尾阈值选取极端收益;HUANG et al.[9]和VAN OORDT et al.[12]以美国股票市场除金融行业外的股票历史收益作为滑动估计窗,同样以5%分位点选取极端收益,或直接选取固定数量的极端收益,利用Hill估计[25]等POT方法估计极值指数作为股票当月的尾风险。首先,KELLY et al.[10]认为所有股票在横截面具有相似的尾风险,相当于构建了市场层面的尾风险或所有股票共有的尾风险,然而由于上市公司所属行业、资本结构、经营策略等不同,不同股票在同一时期所承担的尾风险必然有所差异。其次,选取固定的分位点或固定数量的极端收益忽略了收益分布厚尾程度和偏态程度的时变性。尽管陈国进等[11]和KELLY et al.[10]选取厚尾阈值的做法不同,仿照花拥军等[26]使用的峰度法确定动态阈值,然而峰度法无法刻画分布的偏态程度。再次,RESNICK[27]研究表明,HUANG et al.[9]所用的POT方法对厚尾阈值选取很敏感,不合理的阈值会导致估计结果严重有偏,因而如何准确选取厚尾阈值成为POT方法的难点。
①本研究假设极端收益服从广义极值分布,利用BM方法以FF3模型的收益残差估计极值指数作为个股尾风险的代理变量。BM方法将样本划分为几个块,利用每个块内的极端值构建估计统计量,避免了POT方法中厚尾阈值的选取问题,而且QI[28]证明BM方法对分块的数量和每个块内极端值的数量都有很好的稳健性。②在度量股票尾风险的基础上,以投资组合分析和横截面回归方法检验尾风险对股票收益的预测能力,在控制规模、交易量、非流动性、特质偏度等股票特征以及短期反转和中期动量等股票历史表现后检验尾风险收益预测能力的稳健性。ANG et al.[29]和左浩苗等[30]发现特质波动率与股票预期收益之间是负向关系,MITTON et al.[13]、BOYER et al.[14]和郑振龙等[15]发现特质偏度与股票预期收益之间也是负向关系,因而对尾风险特质波动率和特质偏度等进行横截面相关性分析也有助于验证尾风险收益预测能力的稳健性。③以FAMA et al.[31]的方法构建尾风险定价因子,发现在FF3因子或Fama-French的5因子(FF5)基础上包含尾风险因子的定价模型与FF3和FF5模型相比,对股票横截面收益有更好的解释能力。
2 尾风险的度量方法
股票价格急剧下跌,一部分源于系统性风险冲击,另一部分源于特质层面的风险冲击。ANDERSEN et al.[32]的研究表明收益变化可以分解为正常的波动变化和极端跳跃变化,因而本研究以市场模型的系统性风险因子捕捉收益的正常波动变化,而系统性风险因子无法解释的部分反映了收益的极端变化。
类似于HUANG et al.[9]和KELLY et al.[10]的研究,从FF3模型无法解释的收益部分提取尾风险,即
Ri,t-rt=αi+β1,iMKTt+β2,iSMBt+β3,iHMLt+εi,t
(1)
其中,Ri,t为i股票t时的收益率,rt为t时的无风险收益率,MKTt为t时的市场因子,SMBt为t时的规模因子,HMLt为t时的账面市值比因子,αi为FF3模型回归的截距项,β1,i~β3,i为各因子对应的系数,εi,t为FF3模型回归的残差项,αi+εi,t为i股票t时的收益中系统性风险因子无法解释的部分。同时,用AR(1)-GARCH(1,1)模型过滤收益残差序列的自相关性和异方差性,即
αi+εi,t=ηi+δiεi,t-1+μi,t
(2)
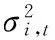
(3)


(4)
其中,x为服从广义极值分布的自变量,R为实数,γ为极值指数。
HILL[25]在假设尾部分布为Pareto分布的前提下,以极大似然估计给出了极值指数γ的估计,即
(5)
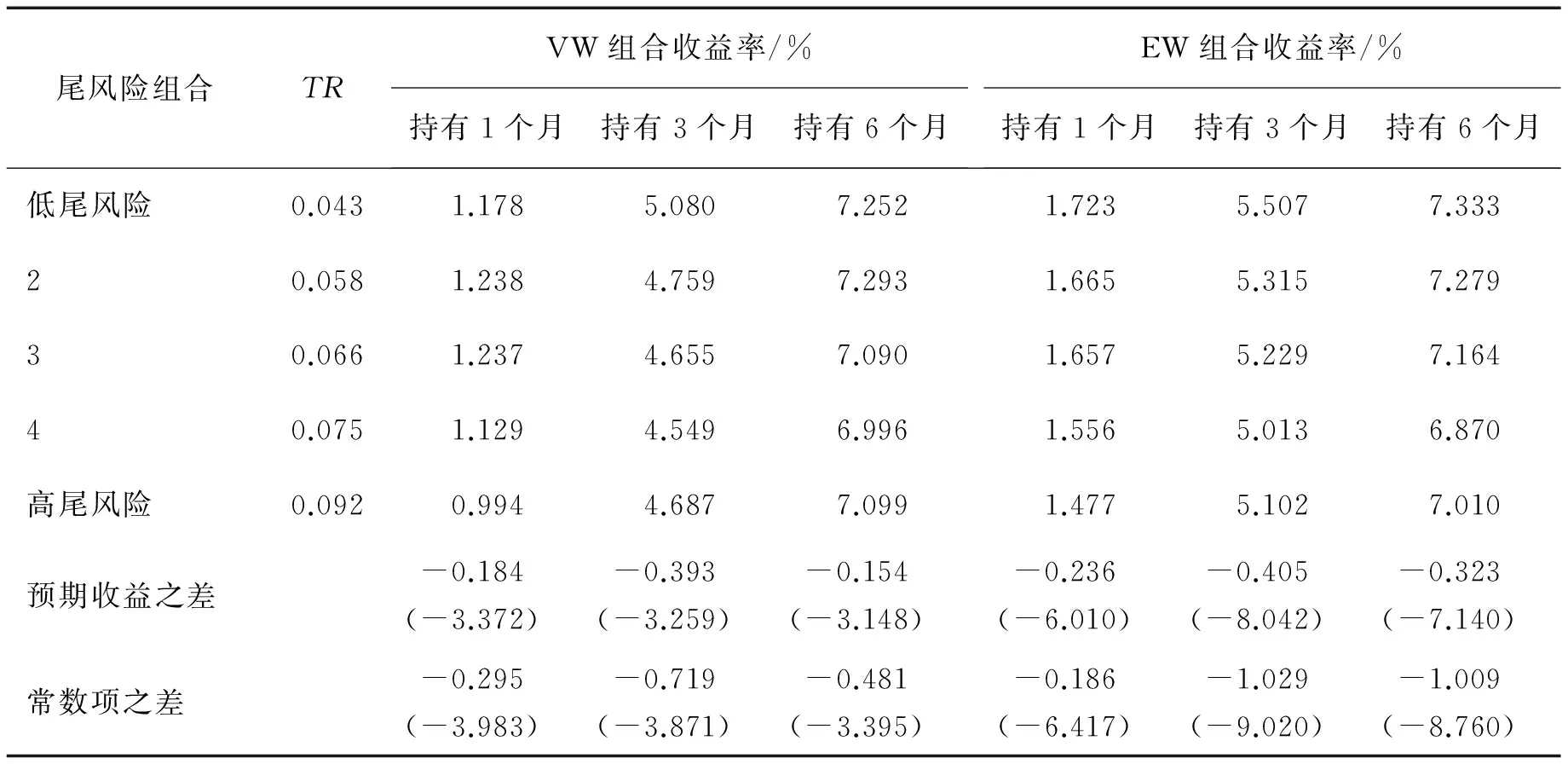
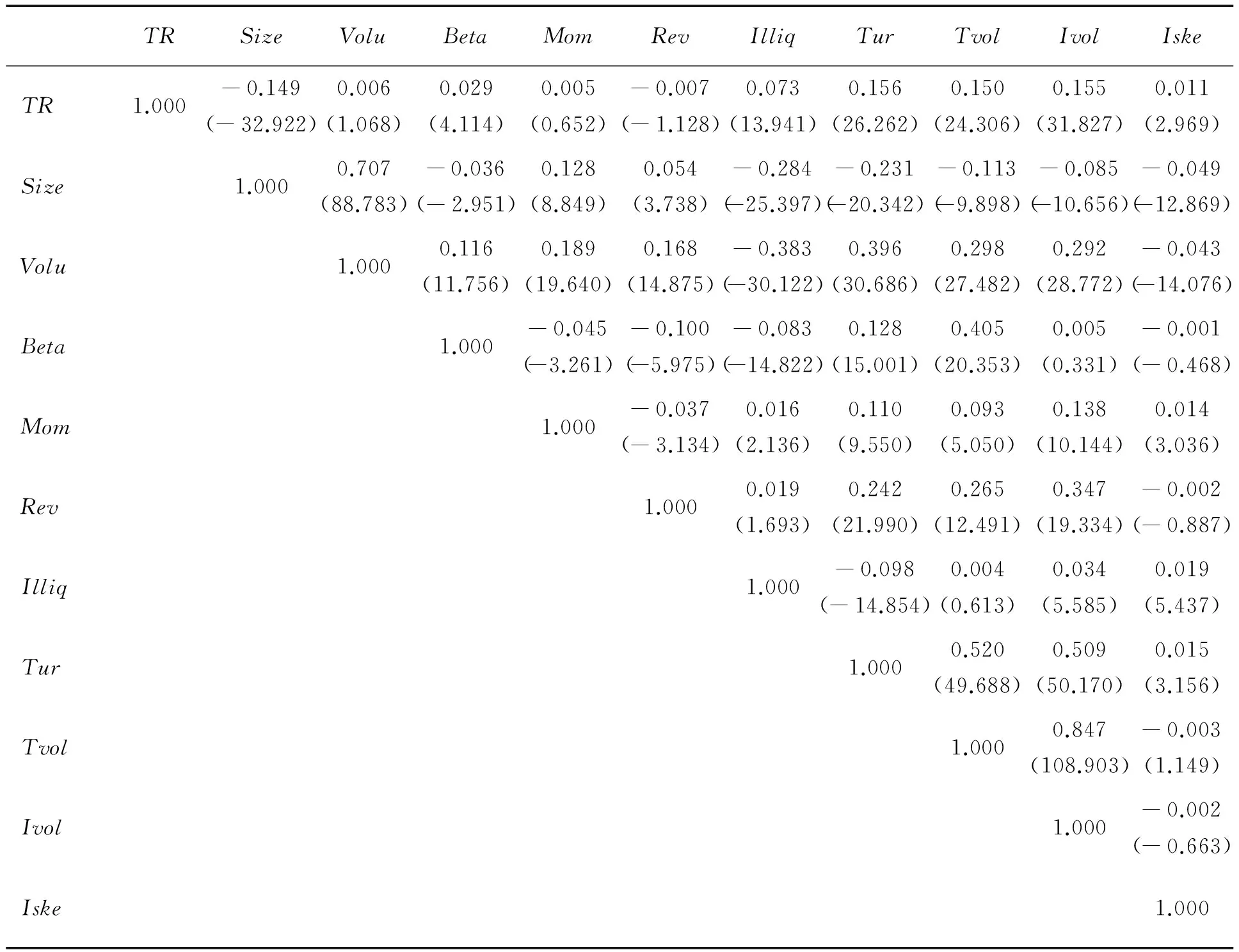
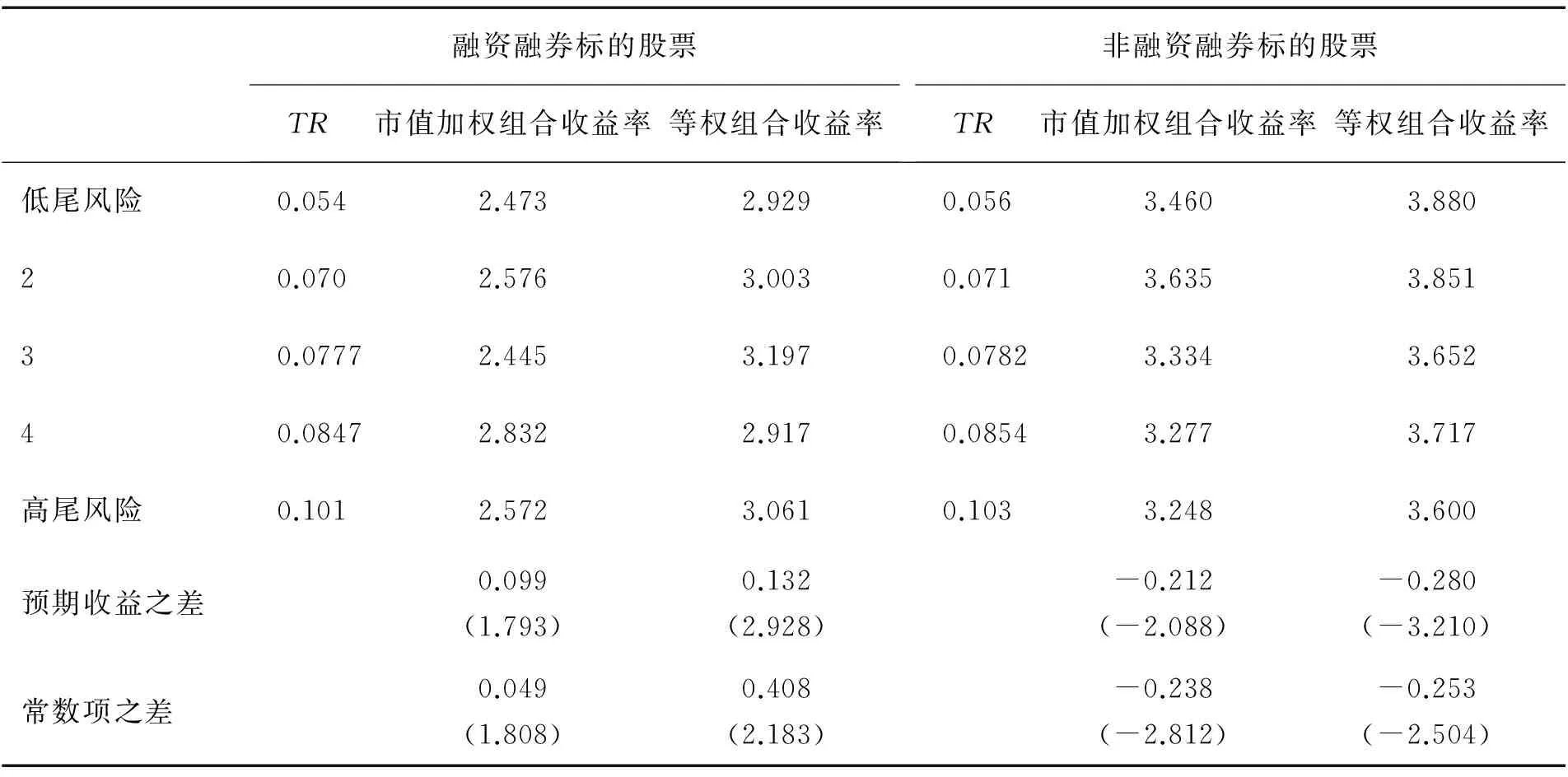
其中,Xn,1≥Xn,2≥…≥Xn,n为随机变量X1,X2,…,Xn的次序统计量;j为估计中超过厚尾阈值的极大次序统计量个数,j=1,2,…,k,k (6) 其中,f为第l块里选取用于估计的极大次序统计量个数,f=1,2,…,d。当d取1时,有 (7) 与Hill估计相比,QI[28]的估计有更小的渐近方差和均方误差,而且对分块的个数kn和每个块内极端值的个数d都有很好的稳健性。 与特质波动率和特质偏度等其他度量收益残差的指标相比,极值指数虽然仅仅利用了收益残差的极端值,然而极端值更加体现收益的变化幅度,而且不同变化幅度的极端值是以不同权重进入估计模型。尽管特质波动率和特质偏度利用了收益残差的所有样本,但是不同样本都是以等权形式进入波动率或偏度的计算式。 本研究选择中国沪深两市A股除创业板之外的所有股票作为研究对象。沪深两市自1996年12月16日开始实行涨停盘制度,这种交易制度的施行会对股票收益变化产生较为复杂的影响,因此,本研究的样本期选择从1997年1月1日至2015年6月30日。初始样本包括2 381只股票共6 069 096条数据,其中跌停的收益数据(≤-10%)只占全部收益数据的0.300%。因此,与陈国进等[11]其他基于中国股票市场研究尾风险的做法一样,忽略涨跌停对尾风险度量及其风险溢价的影响。股票收益、公司特征、无风险收益以及市值因子、账面市值比因子等系统性风险因子数据均来自国泰安CSMAR数据库。 指标计算的细节如下:①以36个月作为BM方法的滑动估计窗,为了保证估计的有效性,要求股票在连续36个月内至少有540个交易日,否则剔除该股票数据。②以每个月作为BM方法的分块,即kn=36。选取d=1,以月内日收益的第1最小值和第2最小值进行左尾极值指数估计。③剔除股票在月内的交易日少于10天的当月股票数据,在此基础上以月内日数据回归CAPM模型得到股票的贝塔,基于FF3模型的回归残差序列计算股票的特质波动率和特质偏度。④以流通市值的自然对数值作为股票的规模,以交易金额的自然对数值作为股票的交易量,以股票(t-6)月~(t-2)月的累积收益作为股票t月的动量指标,以(t-1)月的收益测量t月的收益短期反转。⑤梁丽珍等[35]的研究表明,在中国股票市场AMIHUD[36]的非流动性测度优于其他流动性测度,因此以AMIHUD[36]的测度作为流动性指标。 基于(7)式估计股票的尾风险,并且以流通市值加权计算得到2000年1月至2015年6月共186个月的市场尾风险,发现本世纪以来中国股票市场的尾风险发生了剧烈变化。随着十六届三中全会以后一系列关于资本市场政策的出台,尾风险从2000年1月的0.063一路下降至2003年9月的0.053。之后股票市场一路高歌,尾风险也急剧上升至2006年7月的0.072,增加了约36%。在股票市场牛市和崩盘期间,尾风险都保持在0.070以上的高水平状态。随着市场风险全面释放,2009年3月尾风险开始迅速下降,直至2011年12月下降至0.054后又呈现逐渐上升趋势。从2000年1月至2015年6月,市场尾风险呈现出W形,均值为0.061,最小值为0.053,最大值为0.072,有着高达0.006的方差和0.493的分布偏度。那么,如此跌宕起伏的尾风险对股票收益有什么影响。 本研究先对不同尾风险(TR)组合的特征进行分析,尾风险组合包括规模(Size)、交易量(Volu)、贝塔(Beta)、动量(Mom)、短期反转(Rev)、非流动性(Illiq)、换手率(Tur)、总波动率(Tvol)、特质波动率(Ivol)和特质偏度(Iske)。将2000年1月至2015年6月所有股票按照尾风险从低到高构建十分位组合,组合的各个特征变量见表1。由表1可知,不同尾风险组合的规模、换手率、总波动率和特质波动率都呈现较强的单调性,低尾风险股票组合的规模大,换手率、总波动率和特质波动率都低,高尾风险股票组合的规模小,换手率、总波动率和特质波动率都高,而不同尾风险组合的交易量、贝塔、动量、短期反转、非流动性、特质偏度都不具有明显的趋势性差异。 首先,以投资组合分析方法检验尾风险的收益预测能力。在每个月的月底以尾风险从低到高排序构建5分位组合,以流通市值加权(value-weight,VW)计算组合的尾风险,并且分别持有组合1个月、3个月和6个月,以流通市值加权和等权(equal-weight,EW)计算组合收益,检验高、低尾风险组合的预期收益是否存在差异。为了避免系统性风险报酬对尾风险溢价的影响,进一步以FF3模型对组合收益进行回归,过滤其中的系统性风险溢价后,比较高低组合之间的常数项α是否存在差异,并进行Newey-West-t统计检验[37],结果见表2。 表2中,第2列是以流通市值加权计算的组合尾风险,低尾风险组合的流通市值加权尾风险为0.043,高尾风险组合的流通市值加权尾风险为0.092。第3列是持有组合1个月后的流通市值加权收益,其中低尾风险组合的流通市值加权收益为1.178%,高尾风险组合的流通市值加权收益为0.994%,高、低尾风险组合之间的收益差为-0.184%,相应的Newey-West-t统计量为-3.372,表明高、低尾风险组合的预期收益之间存在显著差异,并且低尾风险组合未来有高收益,而高尾风险组合未来有低收 益。以FF3模型回归组合收益,发现高、低尾风险组合的常数项差异为-0.295%,且相应的Newey-West-t统计量为-3.983,表明调整系统性风险后高、低尾风险组合的异常收益之差依然显著为负。第4列和第5列分别是持有组合3个月和6个月后的流通市值加权收益,高、低尾风险组合的预期收益同样存在显著差异,并且高尾风险组合有低的预期收益,低尾风险组合有高的预期收益,经FF3模型调整系统性风险后负向差异依然显著。表2的后3列是以等权计算尾风险组合的预期收益,同样发现高、低尾风险组合的预期收益存在显著的负向差异。因此,说明尾风险能够显著地负向预测股票收益。 表1 尾风险组合的特征分析结果Table 1 Analysis Results for Characteristics of Stock Portfolios Sorted by Tail Risk 表2 尾风险组合的预期收益分析结果Table 2 Analysis Results for Expected Returns on Stock Portfolios Sorted by Tail Risk 注:括号内数据为Newey-West-t统计量值,下同。 表3 以总收益提取尾风险的组合分析结果Table 3 Portfolio Analysis Results for Tail Risk Extracted from Total Returns 表2是按照HUANG et al.[9]和KELLY et al.[10]的研究方法,从FF3模型的残差项提取尾风险。为了进一步检验尾风险对收益预测能力的稳健性,本研究也按照陈国进等[11]和VAN OORDT et al.[12]的方法,直接以股票的总收益提取尾风险,组合分析结果见表3。与表2的组合分析相类似,在每个月的月底以股票总收益提取的尾风险构建5分位组合,并且分别持有组合1个月、3个月和6个月,发现不论是以流通市值加权计算组合预期收益,还是以等权计算组合预期收益,高、低尾风险组合的预期收益都存在显著的负向差异,即高尾风险组合有低的预期收益,低尾风险组合有高的预期收益。 为了分析尾风险对股票收益负向预测能力的稳健性,本研究用二维投资组合进行进一步检验。先以尾风险之外的股票其他特征作为控制变量构建5分位股票组合,在每一个组合内再以尾风险构建5分位组合,形成5×5二维投资组合,并分别以流通市值加权和等权持有组合1个月。对5个控制变量组合的预期收益进行算术平均,这样不论控制变量较大的股票还是控制变量较小的股票,都被平均分配到按尾风险形成的组合中,即控制变量对不同尾风险组合预期收益的影响被消除。控制其他因素的影响后,检验高、低尾风险组合在持有期的收益是否存在显著的负向差异。为了避免股票的系统性风险报酬对尾风险溢价的影响,在比较组合收益差异的基础上,同样以FF3模型过滤系统性风险溢价后比较常数项α的差异。 表4给出尾风险与股票预期收益关系的二维组合分析结果,第2列至第11列分别为控制规模、交易量、贝塔、动量、短期反转、非流动性、换手率、总波动率、特质波动率和特质偏度的组合预期收益。分别控制规模、交易量、贝塔、动量、短期反转、非流动性、总波动率后,高、低尾风险组合预期收益的负向差异没有明显减弱。尽管在控制换手率、特质波动率、特质偏度后,高、低尾风险组合预期收益的负向差异有所减弱,但是尾风险与股票预期收益之间的负向关系依然显著。不论是高、低尾风险组合的预期收益差异,还是经FF3模型调整系统性风险后的常数项α差异,高、低尾风险组合的预期收益之间都存在显著的负向差异。因此,二维投资组合分析表明尾风险对股票收益有稳健的负向预测能力。 由于股票的各个特征之间存在相关性,二维投资组合分析无法同时控制多个变量对股票预期收益的影响。为了同时检验多个控制变量对尾风险溢价的影响,以尾风险及其他控制变量对股票预期收益进行Fama-MacBeth[38]横截面回归,即 Ri,t+1=ai+biTRi,t+ciControlsi,t+εi,t+1 (8) 其中,Ri,t+1为i股票在(t+1)时的收益,TRi,t为i股票在t时的尾风险,Controlsi,t为i股票在t时的控制变量,包括规模、交易量、贝塔、动量、短期反转、非流动性、 换手率、总波动率、特质波动率和特质偏度,ai为常数项,bi为尾风险的回归系数,ci为控制变量的回归系数,εi,t+1为横截面回归的残差项。 表4 尾风险与股票预期收益关系的二维组合分析结果Table 4 Analysis Results for the Relation between Tail Risk and Expected Stock Returns by Bivariate Portfolios 在进行尾风险和多个控制变量对股票预期收益的横截面回归之前,先对尾风险和控制变量进行相关性检验。在每个横截面计算股票尾风险和控制变量的相关系数,然后在时间序列上检验相关系数的显著性,结果见表5。规模、换手率、总波动率和特质波动率都与尾风险存在较高的横截面相关性,相应的相关系数分别为-0.149、0.156、0.150和0.155。尾风险与贝塔、非流动性和特质偏度也存在显著的正相关性,表明尾风险高的股票风险载荷和非流动性风险也较高,这与表1组合特征分析的结果基本一致。尾风险与交易量、动量和短期反转之间不存在显著的相关性。 根据回归模型控制变量的选取,构建3个不同的横截面回归模型,在每个月以尾风险和其他控制变量对股票未来1个月的预期收益进行回归,计算回归系数的时间序列平均值并进行Newey-West-t统计检验,检验结果见表6。模型中的所有变量以最大值标 准化,被调整为0~1之间的值,样本期从2000年1月至2015年6月,共计186个月。模型1为尾风险对股票预期收益的单变量回归,回归系数为-0.029,相应的Newey-West-t统计量为-3.534,表明尾风险与股票预期收益存在显著的负向横截面关系。在模型2中加入规模等所有控制变量后,尾风险的回归系数为-0.001,相应的Newey-West-t统计量为-2.537,依然显著。与模型1相比,回归系数及其显著性程度都有所降低。规模、交易量、贝塔、动量、短期反转和非流动性的回归系数不显著,而换手率、总波动率、特质波动率和特质偏度的回归系数都显著,因此尾风险与预期收益的负向关系在一定程度上可以被换手率、总波动率、特质波动率和特质偏度的共同作用所解释。模型3保留规模、交易量、贝塔、动量、短期反转和非流动性作为控制变量,发现尾风险的回归系数依然显著为负,表明尾风险具有稳健的负向溢价。 表5 尾风险与股票特征的横截面相关性分析结果Table 5 Cross-sectional Correlation Analysis Results for the Tail Risk and Stock Characteristics 表6 尾风险与股票预期收益的横截面回归分析结果Table 6 Cross-sectional Rregression Analysis Results for the Tail Risk and Expected Stock Returns 在研究样本期内,中国股票市场的交易机制发生了重大变革。2006年6月30日证监会发布《证券公司融资融券业务试点管理办法》,2008年10月5日证监会宣布启动融资融券试点,2010年3月30日上海、深圳证券交易所正式发出通知,将于2010年3月31日起接受券商的融资融券交易申报,融资融券交易正式进入市场操作阶段。截至2015年6月,沪深两市可以融资融券的标的A股已经增至882只。融资融券交易可以增加市场流动性,稳定资产内在价格和规避市场风险。李科等[39]的研究表明卖空限制导致了股价高估,融资融券制度等做空机制有助于矫正被高估的股价,提高市场定价效率;陈海强等[40]考察融资融券制度对中国股市波动率的影响,认为融资融券制度能够有效降低标的个股的波动率;而王朝阳等[41]却发现融资融券会加剧标的个股的波动率。 为了检验这种高杠杆交易模式下尾风险和尾风险溢价的变化,本研究选择2010年4月至2015年6月期间融资融券标的股票和非融资融券标的股票,检验两者之间尾风险和尾风险溢价的差异。通过比较发现,融资融券标的股票与非融资融券标的股票的尾风险存在显著差异,见图1,融资融券标的股票的尾风险显著低于非融资融券标的股票的尾风险,且平均低0.002,相应的t统计量为5.582。 分别以融资融券标的股票的尾风险和非融资融券标的股票的尾风险构建5分位组合,以流通市值加权计算组合的尾风险并持有组合1个月,以流通市值加权和等权计算组合收益,结果见表7。由表7可知,每个融资融券标的股票组合的尾风险都低于非融资融券标的股票组合。对于融资融券标的股票,流通市值加权的高、低尾风险组合预期收益之间不存在显著差异,等权的高、低尾风险组合预期收益之间存在显著的正向差异;对于非融资融券标的股票,高、低尾风险组合预期收益之间依然存在显著的负向差异。由此可见,尽管融资融券交易蕴含复杂的杠杆交易风险、强制平仓风险、监管风险等,但作为一种可选的多样化投资机会和风险规避手段,不仅可以为投资者规避尾风险带来的损失,甚至可以获得尾风险补偿,因此中国资本市场尚未完全开放融资融券交易机制可能是产生尾风险负向溢价的主要原因。进一步,相对于融资融券标的股票,非融资融券标的股票在市场中占大多数,而且平均尾风险溢价的绝对值更大,因此市场整体表现出负向的尾风险溢价。 由于尾风险有负的风险溢价,因此按照FAMA et al.[31]的方法买多尾风险低的组合,并且同时卖空尾风险高的组合,以买多-卖空获得的套利定义尾风险因子(centralized minus dispersive,CMD)。基于稳健性的考虑,本研究以3种方式构建尾风险因子。①将股票分为30%尾风险较低的股票、40%尾风险居中的股票和30%尾风险较高的股票,买多30%尾风险较低的股票组合同时卖空30%尾风险较高的股票组合(CMD30-30);②将股票分为尾风险较低的40%股票、尾风险居中的20%股票和尾风险较高的40%股票,买多40%尾风险较低的股票组合同时卖空40%尾风险较高的股票组合(CMD40-40);③将股票分为尾风险较低的50%股票和尾风险较高的50%股票,买多50%尾风险较低的股票组合同时卖空50%尾风险较高的股票组合(CMD50-50)。 图1 融资融券与非融资融券标的股票的尾风险Figure 1 Tail Risk on Stocks Margin Trading and Stocks Non-margin Trading 融资融券标的股票TR市值加权组合收益率等权组合收益率非融资融券标的股票TR市值加权组合收益率等权组合收益率低尾风险0.0542.4732.9290.0563.4603.88020.0702.5763.0030.0713.6353.85130.07772.4453.1970.07823.3343.65240.08472.8322.9170.08543.2773.717高尾风险0.1012.5723.0610.1033.2483.600预期收益之差0.099(1.793)0.132(2.928)-0.212(-2.088)-0.280(-3.210)常数项之差0.049(1.808)0.408(2.183)-0.238(-2.812)-0.253(-2.504) 首先,分析3种方式定义的尾风险因子与FF5模型的市场风险溢价因子(MKT)、市值因子(SMB)、账面市值比因子(HML)、盈利因子(RMW)、投资因子(CMA)的基本统计量;其次,分析尾风险因子与5因子之间的相关性;最后,以5因子回归尾风险因子,检验5因子对尾风险因子的解释程度,具体结果见表8。A栏中3种方式定义的尾风险因子的均值分别为0.0014、0.0016、0.0013,表明尾风险具有正的平均风险价格,低于风险溢价因子、市值因子和账面市值比因子,而高于盈利因子和投资因子,并且与账面市值比因子、盈利因子、投资因子的标准差都在0.022~0.032之间。B栏表明尾风险因子与市值因子、账面市值比因子、盈利因子有较高的相关性,同时市值因子与账面市值比因子、盈利因子、投资因子也有较高的相关性,盈利因子与投资因子也有较高的相关性。为此,C栏分别以3种方式定义的尾风险因子为因变量,以5因子为自变量进行回归,检验回归模型截距项的显著性。结果显示以尾风险因子为因变量的回归截距项都为正,且Newey-West-t统计检验显著,表明尾风险因子并不能被5因子完全解释。并且,市场风险溢价因子、市值因子、账面市值比因子的回归系数显著,而盈利因子和投资因子的回归系数不显著,表明尾风险因子能够捕捉部分市场风险溢价因子、市值因子、账面市值比因子无法解释的风险溢价,而且与盈利因子和投资因子之间存在正交的风险溢价。 表8 尾风险因子与 FF5因子的基本统计结果Table 8 Summary Statistics Results for Tail Risk Factor and FF Five Factors 注:括号内数据为t统计量。 表9 模型定价效率分析结果Table 9 Analysis Results for Model Pricing Efficiency 本研究以市场模型无法解释的收益残差为样本,以极值理论为基础,提出一种稳健性更好的方法估计极值指数,作为尾风险的代理变量。研究结果表明,尾风险可以负向预测股票收益,而且预测能力具有时间上的持续性,以股票总收益提取尾风险也可以得到一致的结果。控制规模、交易量等股票特征后,尾风险依然稳健地负向预测股票收益,表明尾风险溢价并不能被这些变量所解释。控制反映公司特质层面风险的特质波动率和特质偏度后,尾风险的负向溢价仍然显著,表明尾风险能够捕捉特质波动率和特质偏度之外的特质层面风险。特质波动率和特质偏度对于不同幅度的极端收益都赋予了等权,而尾风险考虑了不同幅度极端收益的不同程度影响。 以买多-卖空组合构建尾风险定价因子,发现相对于风险溢价因子、市值因子、账面市值比因子、盈利因子和投资因子,尾风险因子并不是冗余因子,而且比盈利因子和投资因子的风险价格更高。因此,比较FF3模型、尾风险因子调整的FF3模型、FF5模型、尾风险因子调整的FF5模型的定价效率,尾风险调整的定价模型可以更有效地解释股票横截面收益,证实了尾风险的定价能力。融资融券作为一种能够活跃市场流动性的交易方式,既有比普通交易更为复杂的风险,也可以在一定条件下加快市场的价格发现功能,降低股票的尾风险。稳健性检验表明,融资融券标的股票的尾风险显著低于非融资融券标的股票的尾风险,而且融资融券交易可以在一定程度上解释尾风险的负向溢价。然而由于解释能力较弱,而且目前中国开展融资融券的标的股票占少数,因而市场整体表现出显著的负向溢价。 尽管中国经济依旧保持着高速增长,但是全球经济将持续2008年金融危机后的低迷状态。既有的全球经济治理结构缺乏有效的宏观协调机制,导致各国财政、货币、结构性政策各自为政,同时深陷债务危机的欧洲各国将迎来大选,经济繁荣褪去后难民、恐怖活动等社会矛盾也频频凸显,这些金融市场外部环境的不确定性也将进一步加剧市场尾风险。如何一方面施行合理有效的创新交易机制规避尾风险,另一方面预防交易机制在预防尾风险时的自有风险,将是今后的研究方向。 [1]MANDELBROT B.The variation of certain speculative prices.TheJournalofBusiness,1963,36(4):394-419. [2]FAMA E F.Mandelbrot and the stable Paretian hypothesis.TheJournalofBusiness,1963,36(4):420-429. [3]FAMA E F.The behavior of stock-market prices.TheJournalofBusiness,1965,38(1):34-105. [4]BOLLERSLEV T,TODOROV V.Tails,fears,and risk premia.TheJournalofFinance,2011,66(6):2165-2211. [5]BOLLERSLEV T,TODOROV V,XU L.Tail risk premia and return predictability.JournalofFinancialEconomics,2015,118(1):113-134. [6]BARROSO P,SANTA-CLARA P.Momentum has its moments.JournalofFinancialEconomics,2015,116(1):111-120. [7]RIETZ T A.The equity risk premium a solution.JournalofMonetaryEconomics,1988,22(1):117-131. [8]BARRO R J.Rare disasters and asset markets in the twentieth century.TheQuarterlyJournalofEconomics,2006,121(3):823-866. [9]HUANG W,LIU Q,RHEE S G,et al.Extreme downside risk and expected stock returns.JournalofBanking&Finance,2012,36(5):1492-1502. [10] KELLY B,JIANG H.Tail risk and asset prices.TheReviewofFinancialStudies,2014,27(10):2841-2871. [11] 陈国进,许秀,赵向琴.罕见灾难风险和股市收益:基于我国个股横截面尾部风险的实证分析.系统工程理论与实践,2015,35(9):2186-2199. CHEN Guojin,XU Xiu,ZHAO Xiangqin.Rare disaster risk and asset return:evidence from tail risk in Chinese stock market.SystemsEngineering-Theory&Practice,2015,35(9):2186-2199.(in Chinese) [12] VAN OORDT M R C,ZHOU C.Systematic tail risk.JournalofFinancialandQuantitativeAnalysis,2016,51(2):685-705. [13] MITTON T,VORKINK K.Equilibrium underdiversification and the preference for skewness.TheReviewofFinancialStudies,2007,20(4):1255-1288. [14] BOYER B,MITTON T,VORKINK K.Expected idiosyncratic skewness.TheReviewofFinancialStudies,2010,23(1):169-202. [15] 郑振龙,王磊,王路跖.特质偏度是否被定价?.管理科学学报,2013,16(5):1-12. ZHENG Zhenlong,WANG Lei,WANG Luzhi.Is idiosyncratic skewness priced?.JournalofManagementSciencesinChina,2013,16(5):1-12.(in Chinese) [16] DITTMAR R F.Nonlinear pricing kernels,kurtosis preference,and evidence from the cross section of equity returns.TheJournalofFinance,2002,57(1):369-403. [17] AMAYA D,CHRISTOFFERSEN P,JACOBS K,et al.Does realized skewness predict the cross-section of equity returns?.JournalofFinancialEconomics,2015,118(1):135-167. [18] BARNDORFF-NIELSEN O E,KINNEBROCK S,SHEPHARD N.Measuring downside risk:realized semivariance∥BOLLERSLEV T,RUSSELL J,WATSON M.VolatilityandTimeSeriesEconometrics:EssaysinHonorofRobertF.Engle.Oxford:Oxford University Press,2010:117-136. [19] JACOD J.Statistics and high-frequency data∥KESSLER M,LINDNER A,SØRENSEN M.StatisticalMethodsforStochasticDifferentialEquations.Boca Raton,FL:CRC Press,2012:191-310. [20] CREMERS M,HALLING M,WEINBAUM D.Aggregate jump and volatility risk in the cross-section of stock returns.TheJournalofFinance,2015,70(2):577-614. [21] BAI J,BALI T G,WEN Q.Dothedistributionalcharacteristicsofcorporatebondspredicttheirfuturereturns?.Washington,DC:Georgetown University,2015. [22] ANG A,CHEN J,XING Y.Downside risk.TheReviewofFinancialStudies,2006,19(4):1191-1239. [23] BALI T G,DEMIRTAS K O,LEVY H.Is there an intertemporal relation between downside risk and expected returns?.JournalofFinancialandQuantitativeAnalysis,2009,44(4):883-909. [24] HANSEN B E.Autoregressive conditional density estimation.InternationalEconomicReview,1994,35(3):705-730. [25] HILL B M.A simple general approach to inference about the tail of a distribution.TheAnnalsofStatistics,1975,3(5):1163-1174. [26] 花拥军,张宗益.基于峰度法的POT模型对沪深股市极端风险的度量.系统工程理论与实践,2010,30(5):786-796. HUA Yongjun,ZHANG Zongyi.POT model based on kurtosis and its empirical study on extreme risk of Chinese stock markets.SystemsEngineering-Theory&Practice,2010,30(5):786-796.(in Chinese) [27] RESNICK S I.Heavy-tailphenomena:probabilisticandstatisticalmodeling.New York:Springer Science and Business Media,LLC,2007:78-90. [28] QI Y.On the tail index of a heavy tailed distribution.AnnalsoftheInstituteofStatisticalMathematics,2010,62(2):277-298. [29] ANG A,HODRICK R J,XING Y,et al.The cross-section of volatility and expected returns.TheJournalofFinance,2006,61(1):259-299. [30] 左浩苗,郑鸣,张翼.股票特质波动率与横截面收益:对中国股市“特质波动率之谜”的解释.世界经济,2011,34(5):117-135. ZUO Haomiao,ZHENG Ming,ZHANG Yi.Idiosyncratic volatility and cross-sectional expected return:an investigation of “idiosyncratic volatility puzzle” in China stock market.TheJournalofWorldEconomy,2011,34(5):117-135.(in Chinese) [31] FAMA E F,FRENCH K R.Common risk factors in the returns on stocks and bonds.JournalofFinancialEconomics,1993,33(1):3-56. [32] ANDERSEN T G,BOLLERSLEV T,DIEBOLD F X,et al.Modeling and forecasting realized volatility.Econometrica,2003,71(2):579-625. [34] PAULAUSKAS V.A new estimator for a tail index.ActaApplicandaeMathematicae,2003,79(1/2):55-67. [35] 梁丽珍,孔东民.中国股市的流动性指标定价研究.管理科学,2008,21(3):85-93. LIANG Lizhen,KONG Dongmin.Empirical test on the pricing of liquidity measures in Chinese stock market.JournalofManagementScience,2008,21(3):85-93.(in Chinese) [36] AMIHUD Y.Illiquidity and stock returns:cross-section and time-series effects.JournalofFinancialMarkets,2002,5(1):31-56. [37] NEWEY W K,WEST K D.A simple,positive semi-definite,heteroskedasticity and autocorrelation consistent covariance matrix.Econometrica,1987,55(3):703-708. [38] FAMA E F,MACBETH J D.Risk,return,and equilibrium:empirical tests.JournalofPoliticalEconomy,1973,81(3):607-636. [39] 李科,徐龙炳,朱伟骅.卖空限制与股票错误定价:融资融券制度的证据.经济研究,2014,49(10):165-178. LI Ke,XU Longbing,ZHU Weihua.Short-sale constrains and stock mispricing:the evidences from the margin transactions institution.EconomicResearchJournal,2014,49(10):165-178.(in Chinese) [40] 陈海强,范云菲.融资融券交易制度对中国股市波动率的影响:基于面板数据政策评估方法的分析.金融研究,2015(6):159-172. CHEN Haiqiang,FAN Yunfei.The impact of the launch of margin trading and short selling on Chinese stock market volatility:evidence from a panel-data policy evaluation approach.JournalofFinancialResearch,2015(6):159-172.(in Chinese) [41] 王朝阳,王振霞.涨跌停、融资融券与股价波动率:基于AH股的比较研究.经济研究,2017,52(4):151-165. WANG Chaoyang,WANG Zhenxia.Price limit,margin trading,and stock price volatility:a comparative study between A-shares and H-shares.EconomicResearchJournal,2017,52(4):151-165.(in Chinese) [42] FAMA E F,FRENCH K R.A five-factor asset pricing model.JournalofFinancialEconomics,2015,116(1):1-22. [43] GIBBONS M R,ROSS S A,SHANKEN J.A test of the efficiency of a given portfolio.Econometrica,1989,57(5):1121-1152. FundedProject:Supported by the Education of Humanities and Social Science Research on Youth Fund Project(16YJC790113) and the Philosophy and Social Science of Shanxi Province(2017203) Biography:XING Hongwei, doctor in management, is a lecturer in the Institution of Management and Decision at Shanxi University. His research interests include asset pricing and behavioral finance. His representative paper titled “Investment preference and the idiosyncratic volatility puzzle: evidence from China stock market” was published in theChineseJournalofManagementScience(Issue 8, 2014). E-mail:hongweix@sxu.edu.cn LIU Weiqi, doctor in management, is a professor in the Institution of Management and Decision at Shanxi University and Faculty of Finance and Banking at Shanxi University of Finance and Economics. His research interests include financial engineering and risk management. His representative paper titled “Individual/institutional investor sentiment and stock returns: study based on Shanghai A-share market” was published in theJournalofManagementSciencesinChina(Issue 3, 2014). E-mail:liuwq@sxu.edu.cn WANG Hanying, doctor in management, is a lecturer in the Faculty of Accounting at Shanxi University of Finance and Economics. Her research interests include corporate finance and business ethics. Her representative paper titled “CSR selection after the crises about harm to products: business CSR or philanthropic CSR” was published in theJournalofShanghaiUniversityofFinanceandEconomics(Issue 3, 2016). E-mail:hanyingw1988@163.com
3 数据和尾风险基本统计分析
3.1 数据
3.2 尾风险基本统计分析
4 尾风险的收益预测能力分析
4.1 单变量投资组合分析


4.2 两变量投资组合分析
4.3 横截面回归分析


4.4 融资融券对尾风险溢价的影响
5 尾风险调整的定价模型分析
5.1 尾风险因子

5.2 模型定价效率检验




6 结论

