Exact Solutions to(3+1)Conformable Time Fractional Jimbo–Miwa,Zakharov–Kuznetsov and Modified Zakharov–Kuznetsov Equations

Alper Korkmaz

Department of Mathematics,Çankırı Karatekin University,Çankırı,Turkey

1 Introduction

The particular integer ordered form of the time fractional Jimbo–Miwa(JM)equation of the type

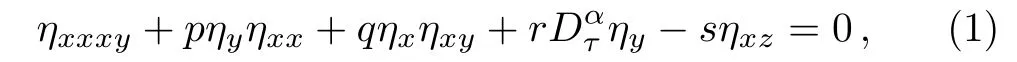
The time fractional Zakharov–Kuznetsov(KZ)equation is of the form

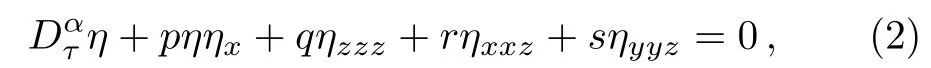
wherep,q,r,andsare real parameters.The original form of the equation has been proposed to define three dimensional ion-sound solitons in a magnetized plasma with a low pressure.[9]The three conservation laws describing mass,momentum and center mass are also formulated in the same study.The ZK equation also admits the ellipsoidal and plane type solitons.[10]Some solutions of the cnoidal,periodic,singular periodic,solitary wave and non topological soliton forms are constructed by using the extended hyperbolic tangent,G′/Gand ansatz methods.[11]The traveling wave solitons in various forms are derived in Ebadi et al.’s study by implementing the exp-function,modified F-expansion andG′/Gmethods.[12]Zhang and Zhou[13]obtains kink,antikink,solitary wave and periodic solutions to the ZK equation in general form by employing the bifurcation theory.

When the nonlinearity of the ZK equation is increased to three,the equation is named as the modified ZK(mZK)equation and the conformable time fractional form of the equation becomes

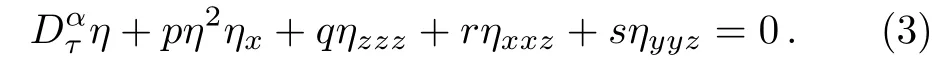
Liang[14]derived some exact solutions in forms of some trigonometric and hyperbolic functions to the mZK equation by using modified simple equation method.More than twenty exact solutions of the mZK equation are derived by using enhancedG′/Gmethod in Ref.[15].The fractional forms of both equations are solved exactly by using improved sub equation adapted for fractional cases.[16]

The related literature contains various methods from Lie symmetries to expansion,ansatz methods or first integral methods for the exact solutions of the nonlinear PDEs.[17−20]The PDE systems can also be solved exactly by using smart techniques like Riemann–Hilbert or Bäcklund transformation methods.These solutions can be in multi soliton solution form.[21−23]Ansatz methods are another technique to construct exact solutions to PDEs even fractional one.[24−26]

In the present study, finite series of a rational exponential function types solutions are derived for the three dimensional fractional PDEs in conformable sense listed above.All the solutions are expressed explicitly.Before explaining the used procedure,some significant descriptions and calculus properties of the conformable derivative are summarized below.

2 Preliminaries

Consider a functionζ=ζ(τ)defined in the positive half space andαbe number ∈ (0,1].Then,the conformable derivative ofζforτ＞0 is defined as

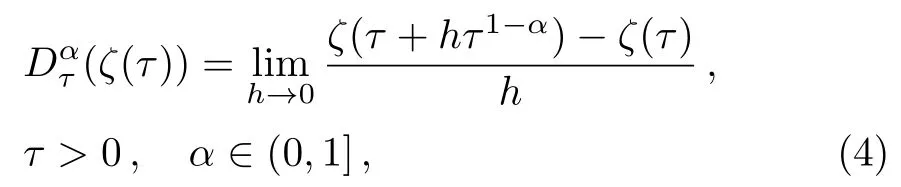
forζ:[0,∞) → R.[27]Even though this definition of the fractional derivative is pretty new,various important properties such as derivative of multiplication and division are defined clearly.The fundamental properties of the conformable derivative required to solve fractional PDEs are summarized below.

Theorem 1Letζ=ζ(τ)andη=η(τ)be twoαdifferentiable functions forα∈ (0,1].Then

for all realc1,c2,c3.[28−29]

The significant properties covering Laplace transform,derivative of composite functions and Gronwall’inequality are defined in Refs.[28,30].

Theorem 2Letζbe a differentiable andα-conformable differentiable function andηalso be defined defined in the range ofζand be differentiable.Then,

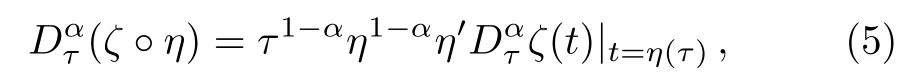
where′denotes the derivative with respect toτ.[28]

3 Modified Kudryashov Method

LetPbe

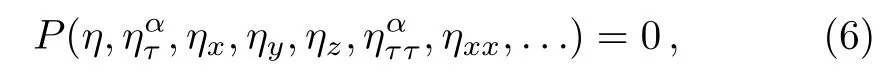
whereη=η(x,y,z,...,τ)andα∈ (0,1]be the fractional derivative order.The transformation

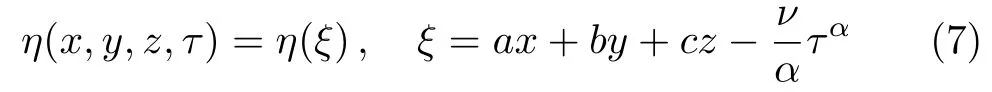
converts(6)to an ODE for new variableξ

where the prime(′)indicates the derivative operator d/dξofηwith respect toξ.[31]

Assume that Eq.(8)has a solution of the form

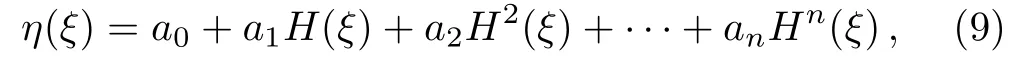
for a finitenwith allai,0≤i≤nandan/=0.The procedure start by determining the degree of the polynomial type seriesnby balancing the non linear term and the highest order derivative term.The functionHis required to satisfy the first-order ODE

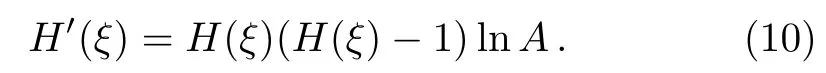
Thus,H(ξ)is determined asH(ξ)=1/(1+dAξ),wheredandAare non-zero constants with the conditionsA＞0 andA/=1.

Substituting the predicted solution(9)and its derivatives into Eq.(8)give a polynomial ofH(ξ).All the coefficients of the powers ofH(ξ)and the constant term are equated to zero.The resultant algebraic equation system is solved fora0,a1,a2,...,anand the other constants used in the wave transformation(7).This method is explained in details in Ref.[32].

4 Solutions to(3+1)-Dimensional JM Equation

The JM equation given in Eq.(1)is reduced to

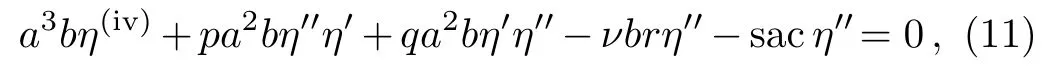
by using the compatible form of the transformation(7).Rearrangement of the last equation by integrating once gives

whereKstands for the constant of integration.The balance between the non linear and the highest ordered terms givesn=1.Accordingly,the predicted solution(9)should be

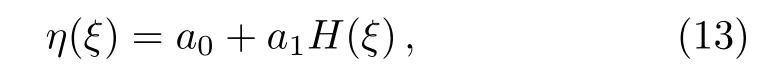
wherea0anda1are the constants to be determined.Substituting this solution and its derivatives into Eq.(1)leads

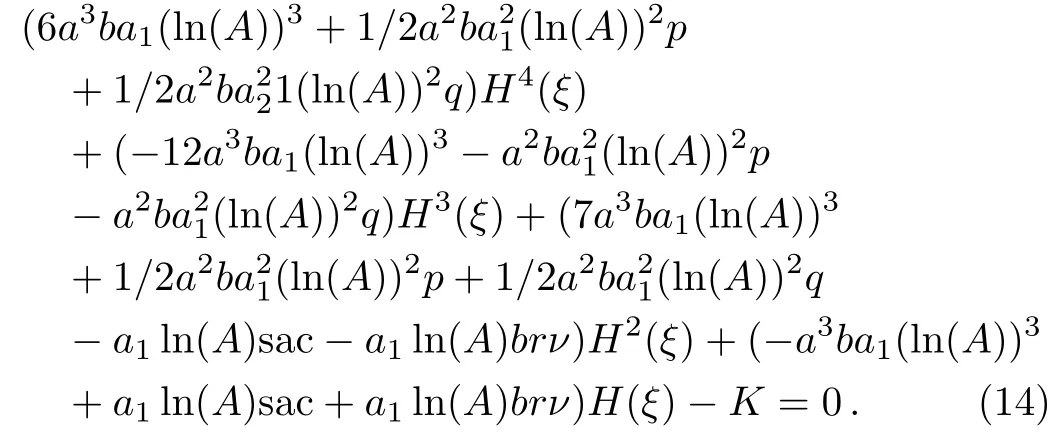
It is clear that anH(ξ)should be nonzero.Hence,the coeffcients of all powers ofH(ξ)andKshould be zero.Thus,the algebraic system of equations

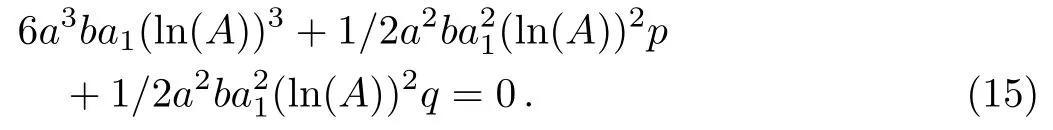
Solving Eq.(15)fora0,a1,a,b,c,νgives

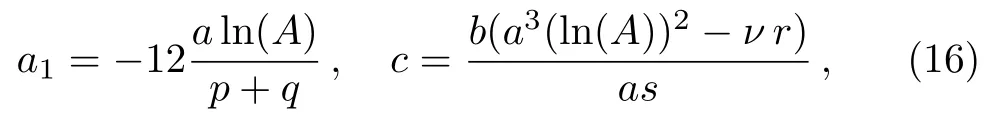
for arbitrary choices ofa0,a,b,νandK=0.The formed solution

gives

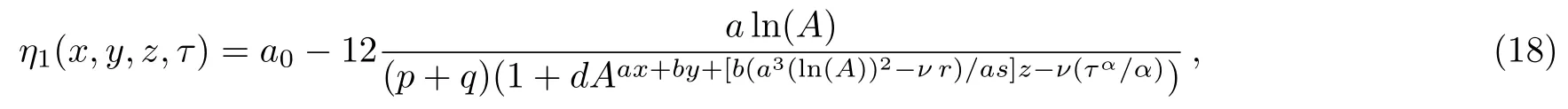
for arbitrarily chosena0,a,b,ν.It must be noted that the system(15)has three more solutions fora1/=0 but at least one ofa,b,c,νare zero in those solution sets.That is why these solutions are not reported here.

5 Solutions to(3+1)-Dimensional ZK Equation

The wave transformation(7)reduces the fractional ZK equation(2)to

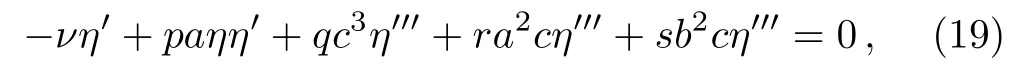
where′denotes d/dξ.Integrating both sides of this equation converts it to

with integration constantK.The balance ofη2andη′′gives the compatiblenas 2.Hence,the predicted solution must be in the formη(ξ)=a0+a1H(ξ)+a2H2(ξ).Substituting this solution into Eq.(20)yields

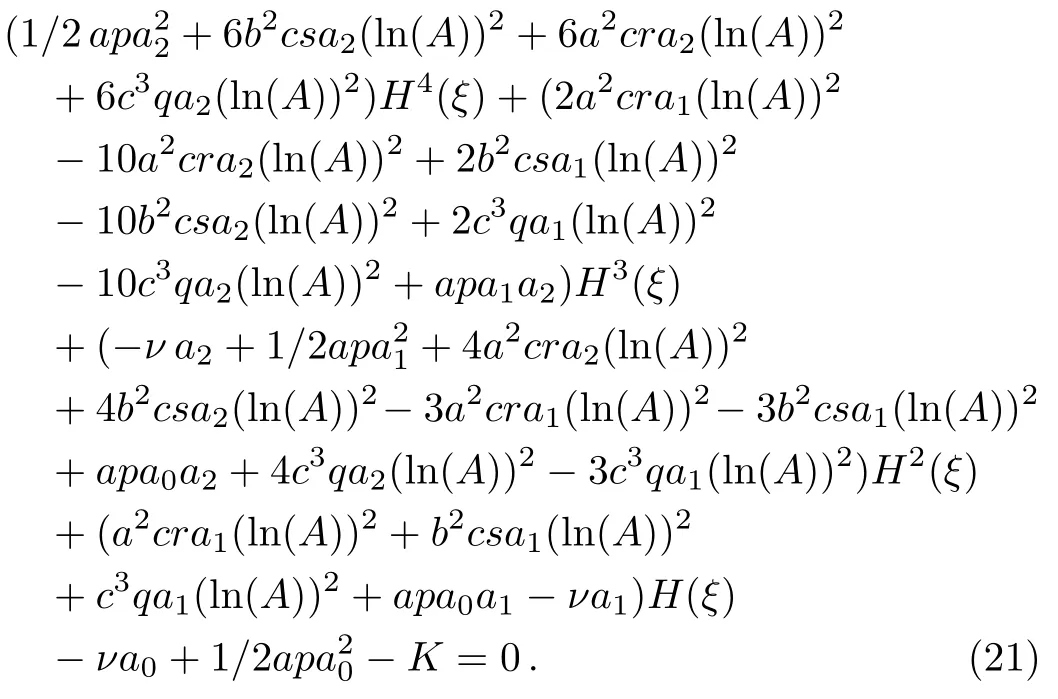
The solution of this system fora0,a1,a2,a,b,c,νgives two different solutions as

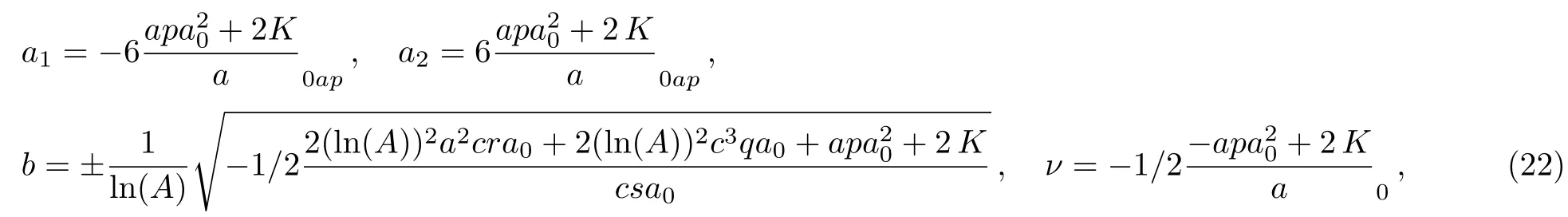
for arbitrary constantsa0,a,c,andK.Thus,the solution of Eq.(20)is determined as

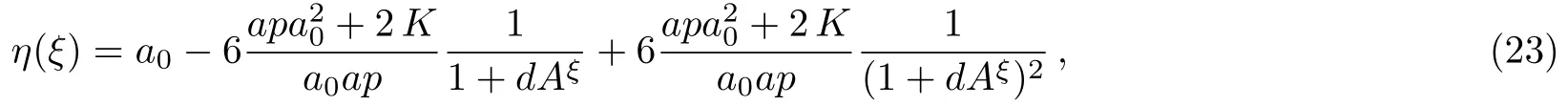
arbitrarya0andK.The solution of the conformable time fractional ZK equation(2)is expressed as

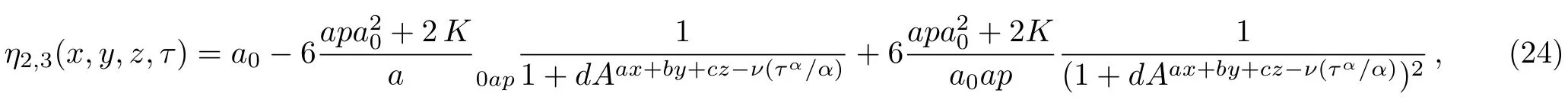
wherea0,a,carbitraryb,νare as given in Eq.(22).

6 Solutions to(3+1)-Dimensional mZK Equation

The modified form of the ZK equation in the time fractional form(3)is reduced to

where′denotes d/dξ.Integrating this equation once converts it to

with the integration constantK.The balance betweenη3andη′′givesn=1.Thus,the solution is formed as

for a nonzeroa1.Substituting this predicted solution and its derivative into Eq.(26),a polynomial equation ofH(ξ)of the form

is obtained.This algebraic system has two different solutions satisfying the conditiona1/=0 and can be written in the form

for arbitrarily chosena,b,c,andK=0.Thus,the solution to Eq.(26)is constructed as

with the condition(qc2+ra2+sb2)c/ap＜0,ap/=0.Hence,the solutions of Eq.(3)are of the form

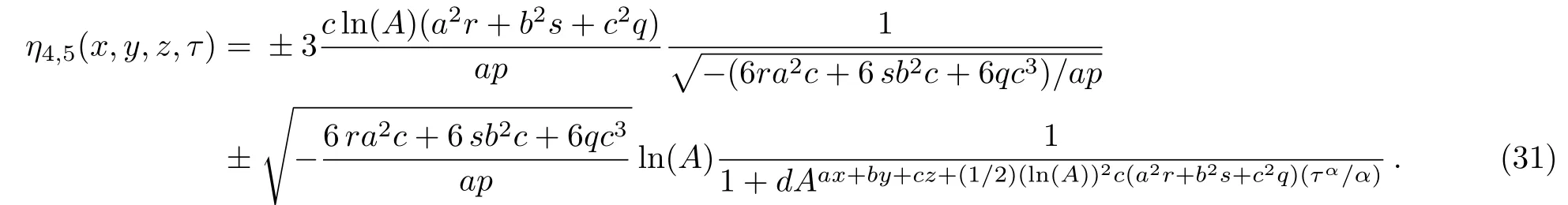
7 Conclusion

The method of Kudryashov in modified form is implemented to derive the exact solutions to(3+1)-dimensional conformable time fractional JM,ZK,and mZK equations.The valid and compatible traveling wave transformation reduces these equations to integer ordered ODEs.The predicted solution of the finite series form of a rational exponential function is substituted into the resultant ODEs.The algebraic operations are used to determine the relations between the coeffcients originated from both the equations and the transformation.Once these relations are determined,the traveling wave type solutions in three dimensions are developed explicitly.

[1]M.Jimbo and T.Miwa,Solitons and In finite Dimensional Lie Algebras,Publ.RIMS,Kyoto Univ.19(1983)943.

[2]B.Cao,Acta Appl.Math.112(2010)181.

[3]Z.Xu and H.Chen,Int.J.Numer.Method H.25(2015)19.

[4]Z.Jie-Fang and W.Feng–Min,Chin.Phys.11(2002)425.

[5]S.H.Ma,J.P.Fang,and C.L.Zheng,Chaos,Solitons&Fractals 40(2009)1352.

[6]W.Hong and K.S.Oh,Comput.Math.Appl.39(2000)29.

[7]T.Özi¸s and˙I.Aslan,Phys.Lett.A 372(2008)7011.

[8]O.T.Kolebaje and O.O.Popoola,African Rev.Phys.(2004)9.

[9]V.E.Zakharov and E.A.Kuznetsov,Zh.Eksp.Teoret.Fiz.66(1974)594.

[10]R.L.Mace and M.A.Hellberg,Phys.Plasmas(1994-present)8(2001)2649.

[11]B.T.Matebese,A.R.Adem,C.M.Khalique,and Biswas,Phys.Wave Phenomena 19(2012)148.

[12]G.Ebadi,A.Mojaver,D.Milovic,S.Johnson,and A.Biswas,Astrophys.Space Science 341(2012)507.

[13]W.Zhang and J.Zhou,ISRN Math.Anal.2012(2012)1.

[14]Y.Liang,J.Interdiscipl.Math.17(2014)565.

[15]M.H.Islam,K.Khan,M.A.Akbar,and M.A.Salam,Comput.Math.Appl.70(2014)158.

[16]S.Sahoo and S.S.Ray,Comput.Math.Appl.70(2015)158.

[17]Q.Zhou,Q.Zhu,A.H.Bhrawy,L.Moraru,and A.Biswas,Optoelectron.Adv.Mater.8(2014)800.

[18]K.Hosseini and P.Gholamin,Diff.Equat.Dyn.Sys.23(2015)317.

[19]Q.Zhou,D.Z.Yao,and Z.Cui,J.Mod.Optics 59(2012)57.

[20]K.Hosseini and Z.Ayati,Nonlinear Sci.Lett.A 7(2016)58.

[21]D.S.Wang,D.J.Zhang,and J.Yang,J.Math.Phys.51(2010)023510.

[22]D.S.Wang and X.Wei,Appl.Math.Lett.51(2016)60.

[23]D.S.Wang,S.Yin,Y.Tian,and Y.Liu,Appl.Math.Comput.229(2014)296.

[24]O.Guner,A.Korkmaz,and A.Bekir,Commun.Theor.Phys.67(2017)182.

[25]A.Korkmaz,Chaos,Solitons&Fractals 96(2017)132.

[26]O.Guner,A.Bekir,and A.Korkmaz,Euro.Phys.J.Plus 132(2017)92.

[27]R.Khalil,M.Al Horani,A.Yousef,and M.Sababheh,J.Comput.Appl.Math.264(2014)65.

[28]A.Atangana,D.Baleanu,and A.Alsaedi,Open Math.13(2015)1.

[29]Y.Çnesiz,D.Baleanu,A.Kurt,and O.Tasbozan,Waves in Random and Complex Media 27(2017)103.

[30]T.Abdeljawad,J.Comput.Appl.Math.279(2015)57.

[31]M.Eslami and H.Rezazadeh,Calcolo 53(2016)475.

[32]N.A.Kudryashov,Commun.Nonlinear Sci.Numer.Simul.17(2012)2248.