Elastic Deformation Analysis on MHD Viscous Dissipative Flow of Viscoelastic Fluid:An Exact Approach

Z.Iqbal,Zaffar Mehmood, and Bilal Ahmad

Department of Mathematics,Faculty of Sciences,HITEC University,Taxila 44000,Pakistan

1 Introduction

The behavior of the boundary layer flow of moving surface has gained considerable attention of the investigators due to its highly applications in industries and engineering.Such type of flow is first examined by Sakiadis.[1]But in particular the boundary layer flow over a stretching sheet has received much attention due to its simple mathematical expression and in many cases its closed form solution also exist(see for example Refs.[2–3]).The applications of boundary layer flow over a stretching sheet are extrusion of plastic sheets,paper production,glass blowing,metallic spinning,drawing plastic films,the cooling of metallic plates in a cooling bath,polymer sheet extruded continuously from a dye and heat treated materials that travel between feed and wind-up rolls.Later,the problem of stretching flow has been extended in numerous ways such as to include MHD effects,heat transfer and mass transfer in flows with or without suction/injection through the sheet.The bibliography on such flows is quite vast and some attempts in this direction can be mentioned in the studies.[4−8]

The theoreticalstudy ofmagnetohydrodynamic(MHD) flow under heat and mass transfer has been a subject of great interest in many technological and industrial applications,particularly when the flow is induced by shearing motion of a wall.Many such flows encounters non-Newtonian fluids.More precisely,in modern metallurgical and metal working process MHD flows caused by a vessels deformation filled with fluids has attained special grounds.Due to vast range of its applications researchers and industrialist has focused on experimental and theoretical analysis of MHD fluid flows in different aspects and such flows are witness in contrast enhancement in magnetic resonance imaging(MRI),thermal therapy for cancer treatment,MHD generators,plasma studies,nuclear reactors,geothermal energy extraction and many others.Many recent attempts have been put forward in this direction in which Alam et al.[9]examined the effects of viscous dissipation and Joule heating in steady MHD flow over an inclined radiate isothermal permeable surface in the presence of thermophoresis.Hayat et al.[10]examined the influence of thermal radiation and Joule heating on MHD flow of Maxwell fluid with thermophoresis.Aliakbar et al.[11]studied the influence of thermal radiation on MHD flow of Maxwellian fluids above stretching sheets.Some other recent investigations are in Refs.[12–16].

A wide range of materials manifest some fluid characteristics that cannot be represented by Newtonian fluid models.Such fluids that have not such characteristics are generally called non-Newtonian fluids.Geophysical applications are based on non-Newtonian constitutive behaviors.The governing equations for non-Newtonian fluids are in general of higher order and more complicated than the Navier–Stokes equations.These equations have been used to models such problems and analyzed various characteristics like stretching/shrinking sheet,heat transfer,mass transfer,viscous dissipation,the effect of electric and magnetic field.These have been concerned with ice and magma flows,designing cooling systems with liquid metals,MHD generators,accelerators and pumps.There is a class among the many constitutive assumptions thathave been employed to study non–Newtonian fluid behavior that has gained support from both the experimentalists and the theoreticians is that of second grade fluid for which one can reasonably hope to obtain closed form solution.[17−18]

Newtonian heating orconjugateconvective flow(Merkin[19])is heat transfer rate from bordering plate with a finite heat capacity,which is proportional to local surface temperature comparable heating adapt.Lesnic et al.[20]and Pop et al.[21]discussed oblige convection boundary layer streaming of viscous fluid stuffng porous medium using Newtonian heating.An exact solving for unsteady boundary layer flow of a viscous fluid with Newtonian heating observed by Chaudhary and Jain.[22]Salleh et al.[23−24]studied forced convection boundary layer flow at an impudent stagnation-point with Newtonian heating.Salleh and Nazar[25]analyzed free and mixed convection boundary layer flows for circular cylinder with Newtonian heating.Some recent articles are Refs.[26–27].

In view of above conversation,this analysis is primarily intended to discuss an exact approach of MHD flow of second grade fluid with non-uniform heat source/sink and elastic deformation with Newtonian Heating.Calculations are performed for exact solutions of velocity and temperature.To the authors knowledge such exact solutions have not been reported previously in the literature.Results of velocity,temperature and concentration profiles are analyzed for physical parameters.Note that the problem of heat transfer in non-Newtonian fluid has practical importance in many industries,for example in paper making,drilling of petroleum products,slurry transporting of food and polymer solutions.

2 Problem Development and Governing Model

We consider the steady boundary layer flow of an incompressible second grade fluid induced by a stretching surface.The sheet is situated aty=0 and stretched with velocityuw(x)=ax,(whereais positive constant).Flow is con fined toy≥0 and uniform magnetic field with strengthB0is applying in the perpendicular direction to the flow.Negligible magnetic Reynolds number is taken into account so that induced magnetic field is neglected.Heat transfer in the presence of Newtonian heating is considered.Furthermore,we assumed that concentrationCtakes constant valueCwat the wall and ambient value of concentration isC∞.In addition,T∞is considered as free stream temperature.Physical flow phenomena is presented in Fig.1.

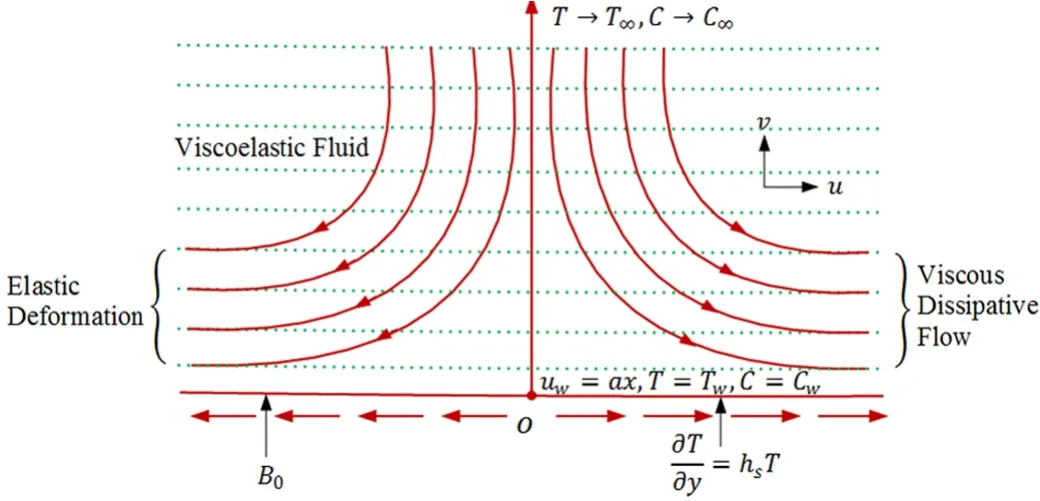
Fig.1 Physical flow diagram.

By applying boundary layer approximation the governing equations for the flow,heat and mass transfer of an incompressible second grade fluid are defined as(see Mahmood et al.[17]and Nandeppanavar[18])

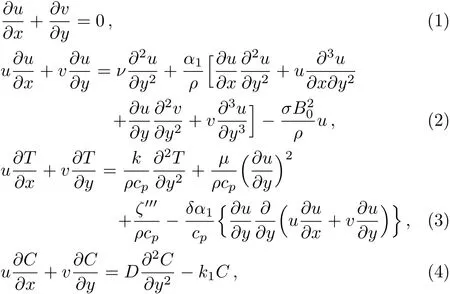
subject to boundary conditions

In above expressionsuandvare the velocity components in thex-andy-directions,α1the second grade parameter,Tis fluid temperature,kis thermal conductivity of the fluid,cpis specific heat,hsis heat transfer temperature,ν=(µ/ρ)is kinematic viscosity,andρis density of the fluid,σis electrical conductivity,δis coeffcient of elastic deformation,Cis concentration of fluid,Dis the effective diffusion coeffcient,k1is the first order chemical reaction rate andζ′′′is the space and temperature dependent internal heat generation/absorption which can be expressed as

whereA∗andB∗are coeffcients of the space temperature dependent internal heat generation/absorption.The caseA∗＞0 andB∗＞0 correspond to internal heat generation whileA∗＜0 andB∗＜0 correspond to internal absorption,Twis temperature of the sheet andT∞is the temperature of fluid far away from the sheet andf′is derivative of velocity with respect toηwhich are introduced by(see Alsaedi et al.[3])

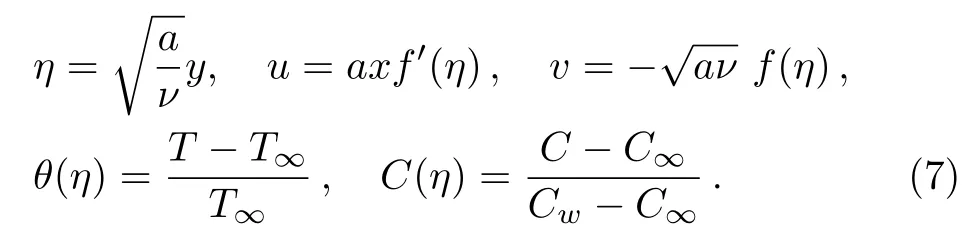
Equation(1)is automatically satis fied and Eqs.(2)–(4)can be written as

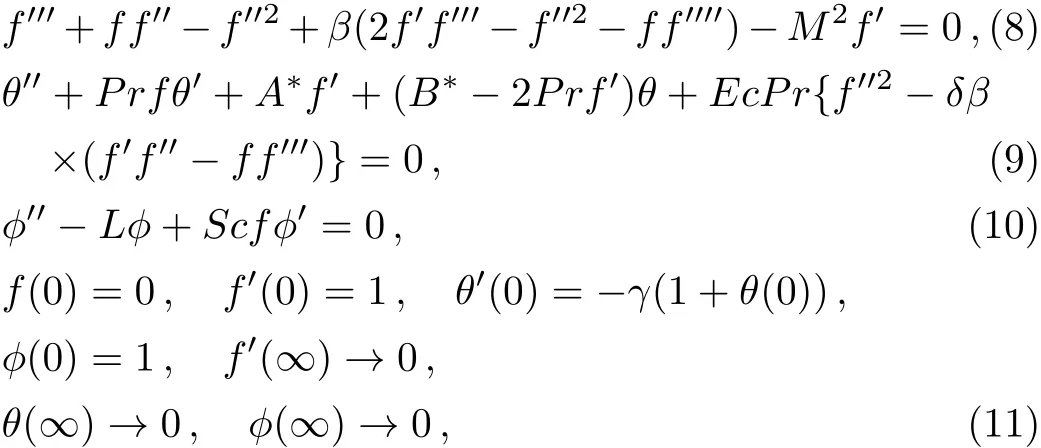
wherePris Prandtl number,Mis local Hartman number,Lis chemical reaction parameter,Dis Schmidt number,γis conjugate parameter for Newtonian heating,Ecis Eckert number,andβis second grade fluid parameter.These are defined as

The skin friction coeffcientCf,local Nusselt numberNux,and local Sherwood numbersShxare defined by

where the wall skin frictionτw,heat transferqwand mass transfercwfrom the plate are given by

In view of Eq.(7),the above expressions expressed in Eqs.(13)–(15)provide in dimensionless form as

whereRex=ax/νis the local Reynolds number.

3 Closed Form Solutions

3.1 Momentum Boundary Layer Problem

Proposed exact solution[17−18]for Eq.(8)is

which satisfies the boundary conditions explained in Eq.(11)By using these boundary conditions(11)we have

Thus the exact solution for the flow is

and skin friction at the wall is

3.2 Temperature Boundary Layer Problem

The solution of energy Eq.(9)subject to boundary conditions,which are explained in Eq.(11)in terms of con fluent hypergeometric function can be expressed as

in which

and heat transfer flux at the wall is

3.3 Concentration Boundary Layer Problem

Invoking Eq.(20)in Eq.(10)we arrived at

with boundary conditions

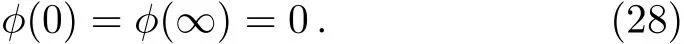
We introduceξ=Scexp(−Kη)/K2and substituting it into Eq.(27),we get the following exact solution

in which1F1are the confluent hypergeometric functions.Furtherκ1andκ2are defined by

Solution of Eq.(29)in terms ofηcan be written as

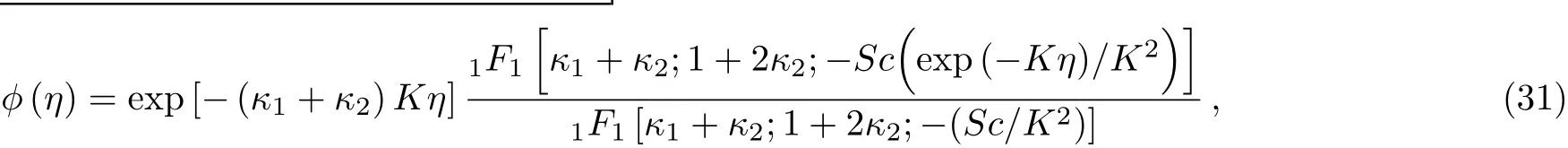
with mass transfer flux at the wall is

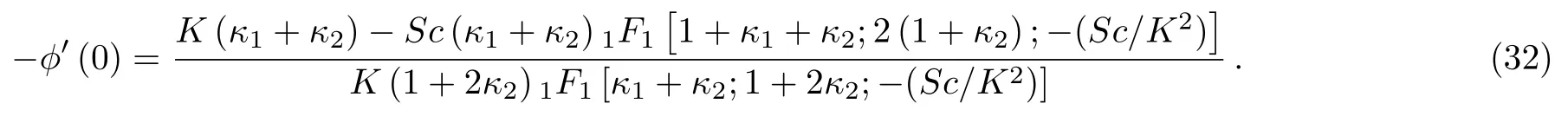
4 Theoretical Results and Physical Description

Fig.2 Impact of M on f′(η).

This section is devoted to graphical results and their discussions for effects of significant parameters involved in the flow of second grade fluid.Figures 2 and 3 illustrate the contribution of Hartman numberMand fluid parameterβon axial component of velocity.MHD being resistive force implies to lesser fluid flow whileβbeing a second grade parameter plays a role in enhancing fluid velocity.Figures 4–17 are plotted to demonstrate influence of various notable parameters on thermal boundary layer.Figures 4–7 are graphical representation of coeff-cients of space and temperature dependent internal heat generation/absorption in the presence and absence of elastic deformation,respectively on temperature profile.From Figs.4 and 5,it is observed that coeffcient of space dependent internal heat generationA∗ampli fies the temperature profile,whereas,change in the thermal boundary layer has minor effect in the presence of elastic deformation as compared to the absence of elastic deformation.Same is the case for the temperature dependent internal heat generation coeffcientB∗.This happens mainly due to the phenomenon of internal heat generation,which contributes in upsurging temperature distribution.Figures 8 and 9 figure outηversus temperature profileθ(η)for different values of fluid parameterβwith(δ=1)and without(δ=0)elastic deformation,respectively.From these figures,it is apparent that the temperature profile shorten with rise of value of fluid parameter.This is because of the fact that an increase of viscoelastic normal stress gives rise to thickening of the thermal boundary layer.Figures 10 and 11 reveal that thermal boundary layer ascend with grow in the value of Eckert numberEc.In other words,thermal dissipation shortens with an increase inEc.This is because boosting inEcthe heat dissipation less significant,which affects in growing temperature of fluid.When elastic deformation is negligible the heat dissipation affects less as compare to the presence of elastic deformation.

Fig.3 Impact of β on f′(η).

Fig.4 Impact of A on θ(η),δ=1.0 with elastic deformation.

Fig.5 Impact of A∗ on θ(η),δ=0 without elastic deformation.

Fig.6 Impact of B∗ on θ(η),δ=1.0 with elastic deformation

Fig.7 Impact of B∗ on θ(η),δ=0 without elastic deformation.

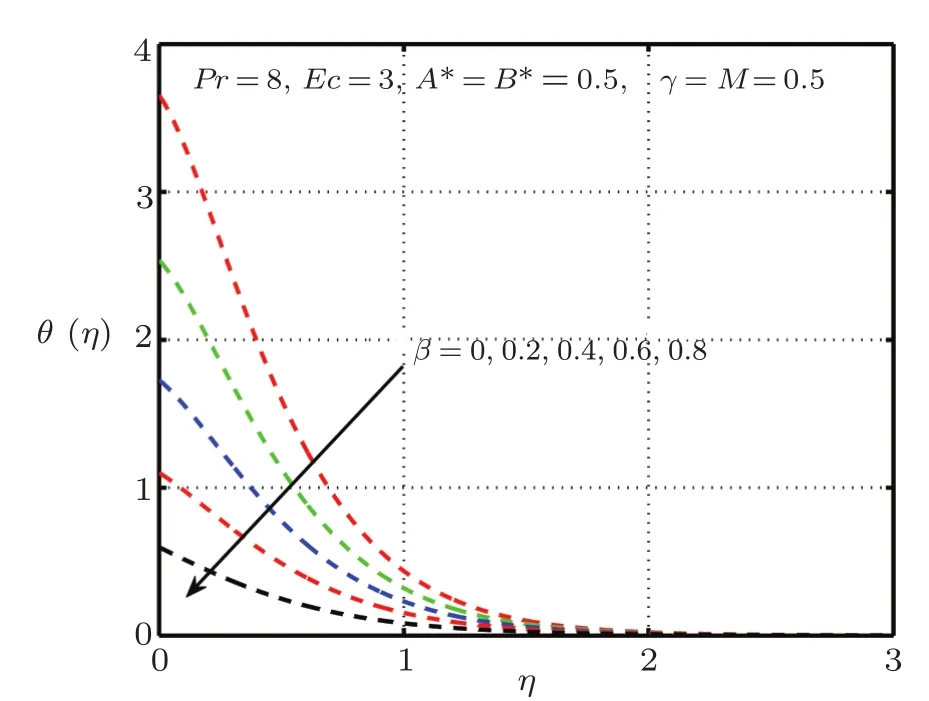
Fig.8 Impact of β on θ(η),δ=1.0 with elastic deformation.

Fig.9 Impact of β on θ(η),δ=0 without elastic deformation.

Figures 12 and 13 characterize the impact of conjugate parameter for Newtonian heatingγin the presence and absence ofδ,respectively.From these figures,it is obvious that with higher values ofγcauses enlarge in the internal temperature of the flow and hence temperature profile raise significantly.The temperature profile for distinct values of Prandtl numberPrexhibit in Figs.14 and 15.It is noted that asPris enhanced,the temperature profile shortens.It is also expressed from these figures that thermal boundary layer thickness grows with reducing Prandtl number i.e.,for small value ofPr(≪1), fluid is highly conductive.The influence of elastic deformation of large magnitude on temperature profile is demonstrated in Fig.16.

Fig.10 Impact of Econ θ(η),δ=1.0 with elastic deformation.

Fig.11 Impact of Econ θ(η), δ=0 without elastic deformation.

Fig.12 Impact of γ on θ(η),δ=1.0 with elastic deformation.

Fig.13 Impact of γ on θ(η),δ=0 without elastic deformation.

Fig.14 Impact of Pr on θ(η),δ=1.0 with elastic deformation.

Fig.15 Impact ofPr onθ(η),δ=0without elastic deformation.

It is examined that when the elastic deformation has greater magnitude,the temperature profile significantly down due to the fact that temperature goes up with add in stress caused by elasticity.From Fig.17 it is proved that temperature mounts rapidly when magnitude of magnetic force get higher.Figures 18–21 explain the importance of concentration for diverse values ofβ,L,ScandM.Figures 18 and 21 exhibit ascending behavior of concentration profile against intensified values ofβandMwhereas from Figs.19 and 20 reverse behavior is seen in the case ofScandL.

Fig.16 Impact of δ on θ(η).

Fig.17 Impact of δ on θ(η).

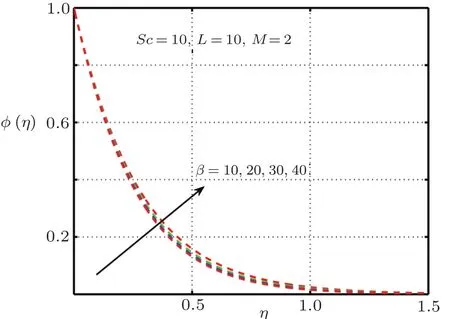
Fig.18 Impact of β on φ(η).

Fig.19 Impact of β on φ(η).

Fig.20 Impact of Sc on φ(η).

Fig.21 Impact of M on φ(η).

5 Conclusions and Novelty of Article

In the present article heat transfer analysis was carried out in a second grade fluid towards an impermeable extending surface with non-uniform heat source/sink and elastic deformation.Governing nonlinear system of partial differential equations was simplified to system of nonlinear ordinary differential equations.Exact solutions were derived in form of con fluent hypergeometric function.Key findings of present analysis include:Increase in the Prandtl number and elastic deformation parameter decreases temperature and thickness of thermal boundary layer.Temperature and thermal boundary thickness are an increasing functions of non-uniform heat source/sink Eckert,Conjugate and Schmidt numbers.Second grade parameter increases velocity,thermal and concentration boundary layer thickness.Hartman number contributes in lowering viscous boundary layer whereas it effects thermal and concentration boundary layers in an opposite manner.Chemical reaction parameter plays a role in reducing concentration profile.Space and temperature heat source/sink coeffcients enhance temperature profile.Significant increase is notable in absence of elastic deformation.

[1]B.C.Sakiadis,AIChE J.7(1961)221.

[2]M.Turkyilmazoglu and I.Pop,Int.J.Heat Mass Transfer 56(2013)1.

[3]A.Alsaedi,Z.Iqbal,M.Mustafa,and T.Hayat,Z.Naturforsch 67a(2012)517.

[4]Z.Mehmood and Z.Iqbal,J.Mol.Liq.224(2016)1083.

[5]Z.Iqbal,E.Azhar,Z.Mehmood,E.N.Maraj,and A.Kamran,J.Mol.Liq.230(2017)295.

[6]Z.Iqbal,M.Qasim,M.Awais,T.Hayat,and S.Asghar,J.Aerospace Eng.29(2015)04015046.

[7]T.Hayat,Z.Iqbal,M.Qasim,and A.A.Hendi,Zeitschrift für Naturforschung A 67a(2012)217.

[8]E.Azhar,Z.Iqbal,and E.N.Maraj,Zeitschrift für Naturforschung A 71(2016)837.

[9]M.S.Alam,M.M.Rahman,and M.A.Sattar,Comm.Nonlinear Sci.Num.Simul.14(2009)2132.

[10]T.Hayat and M.Qasim,Int.J.Heat Mass Transfer.53(2010)4780.

[11]V.Aliakbar,A.A.Pahlavan,and K.Sadeghy,Commun.Nonlinear.Scien.Numer.Simul.14(2009)779.

[12]H.S.Hassan,S.A.Mahrous,A.Sharara,and A.Hassan,Appl.Math.Inf.Sci.9(2015)1327.

[13]V.Kumaran,A.V.Kumar,and I.Pop,Comm.Nonlinear Scien.Numer.Simul.15(2010)300.

[14]N.S.Akbar,Z.Khan,S.Nadeem,and W.Khan,Int.J.Numer.Meth.Heat Fluid Flow 26(2016)108.

[15]N.S.akbar,D.Tripathi,Z.H.Khan,and O.A.Beg,Chem.Phys.Lett.661(2016)20.

[16]N.S.Akbar and Z.H.Khan,J.Magn.Mag.Mat.378(2016)320.

[17]A.Mahmood,S.Parveen,and N.A.Khan,Acta Mech.Sin.27(2011)222.

[18]M.M.Nandeppanavar,M.S.Abel,and J.Tawade,Commun.Nonlinear Sci.Numer.Simulat.15(2010)1791.

[19]J.H.Merkin,Int.J.Heat Fluid Flow 15(1994)392.

[20]D.Lesnic,D.B.Ingham,and I.Pop,Int.J.Heat Mass Transfer.42(1999)2621.

[21]I.Pop,D.Lesnic,and D.B.Ingham,Hybrid Meth.Eng.2(2000)31.

[22]R.C.Chaudhary and P.Jain,J.Eng.Phys.Thermophys.80(2007)954.

[23]M.Z.Salleh,R.Nazar,and I.Pop,Chem.Eng.Commun.196(2009)987.

[24]M.Z.Salleh,R.Nazar,and I.Pop,Heat Mass Transfer 46(2010)1411.

[25]M.Z.Salleh and R.Nazar,Sains Malays 39(2010)671.

[26]N.S.Akbar and Z.Khan,J.Mol.Liq.222(2016)279.

[27]S.Rana,R.Mehmood,and N.S.Akbar,J.Mol.Liq.222(2016)1010.