Borromean Windows for Three-Particle Systems under Screened Coulomb Interactions∗
2018-01-24ZiShiJiang姜子实XiuDanSong宋秀丹LinZhou周林andSabyasachiKarCollegeofPhysicalScienceandTechnologyHeilongjiangUniversityHarbin150080ChinaDepartmentofPhysicsHarbinInstituteofTechnologyandCenterforTheoreticalAtomicandMolecularPhy
Zi-Shi Jiang(姜子实), Xiu-Dan Song(宋秀丹), Lin Zhou(周林), and Sabyasachi KarCollege of Physical Science and Technology,Heilongjiang University,Harbin 150080,China Department of Physics,Harbin Institute of Technology,and Center for Theoretical Atomic and Molecular Physics,Academy of Fundamental and Interdisciplinary Sciences,Harbin Institute of Technology,Harbin 150080,China
1 Introduction
In the present study,we have made an attempt to search Borromean windows(BWs)for the H+2-like and muonic molecular ions interacting with Screened Coulomb(Yukawa-type)potentials.Borromean states in a threebody system exits if it is bound while all the two-body subsystems are unbound.[1−6]Borromean window(BW)for a three-body system can be identified by observing Borromean states in this system and all of its two-body subsystems.[5−11]Borromean binding is related to a fascinating phenomenon in nuclear physics which is known as Efimov effect.[12−17]It is well-known that the Efimov effect is a direct consequence of the different ranges of the interacting potentials and it emerges from the resonant coupling of two-body interactions.[13]The existence of Efimov effect[12]for a three-body system indicates that when the two-body energy vanishes,a myriad of weakly bound states appears in the three-body spectrum.[1]Evidence of the Efimov effect was found in the recombination processes in ultracold atomic gases.[14]The Efimov state in the helium trimer has also been observed.For details studies on the Efimov effects in cold atoms or molecules,interested readers are referred to the review articles of Chen[14]and Hammer.[15]Appearance of Borromean states in halo nuclei has been discussed in the previous work.[16]It should be mentioned in this context that cold atoms and halo nuclei share common features in their respective low energy regimes.Borromean binding is also associated with an interesting phenomenon,which is termed as Thomas collapse,[17]for a very small two-body binding the three-body energy becomes in finite upon reducing the potential range.In spite of several applications in nuclear physics,[18]Borromean systems also appear in molecular physics,[19−20]chemical physics,[21]and DNA.[22]
Studies with screened potentials are relevant and useful in many areas of physical sciences.[23−32]Screened potentials are applied to approximate many-body interactions in simple models. Among the set of screened potentials,one of the most important,both historically and practically,is the statically screened Coulomb potential,or Yukawa potential of the form:Ze−λ/r/r,whereZ=q1q2,q1andq2being the charges of the interacting particles.In plasma physics,this potential is known as the Debye–Hückel potential and used to represent the screening effects between charged particles.[33−35]The potential is used also in condensed matter physics,mainly,to sketch electronic properties in metals[36]and to model colloidal suspensions.[37]Detail calculations for the Borromean binding using screened Coulomb potentials(SCP)can be found from earlier investigation.[1−3,38−45]
Several studies have been performed on the Borromean binding ofwith SCP.[1−2,5−10,39−42]Mukherjee etal.[10]investigated the Borromean states forinteracting with SCP.Kar and Ho[6−7,9]reported the Borromean binding offorJ=0,1,2,3 states using exponential correlated wave functions.Ghoshal and Ho[39]studied the Borromean binding forJ=0 states using Hylleraas-type wave function.Mukherjee et al.[5,43−44]reported the Borromean states for muonic molecular ions ppµ,ddµand ttµ.They have also reported the Borromean states forandions.[5]Kar and Ho[46−48]also studied the bound states for exotic molecular ions.Kar and Ho[38]also investigated the BWs for three self-gravitating boson and fermion systems.Ghoshal and Ho[49]reported the BWs for ppµ,ddµ,ttµ,tdµions interacting with SCP.However,the Borromean bindings for HD+,HT+,DT+,pdµand ptµsystem interacting with SCP have not been studied yet.With recent advances on the studies of Borromean states inand muonic molecular ions,it is also of interest to estimate these states for-like and muonic molecular ions interacting with screened Coulomb(Yukawa-type)potentials.
In the present study,we have estimated the Borromean windows for thetdµ,ptµ,pdµ,ppµ,ddµ,ttµinteracting with SCP.We have calculated the boundJ=0 states energies for different screening parameters using Hylleraas-type wave functions in the framework of Ritz variational principle.Convergence of our calculations has been examined with the increasing number of terms in the basis expansions.Atomic units are used throughout the work,unless stated otherwise.
2 Calculations
The non-relativistic screened Hamiltonian for the hydrogen and muonic molecular ions interacting with SCP is given by
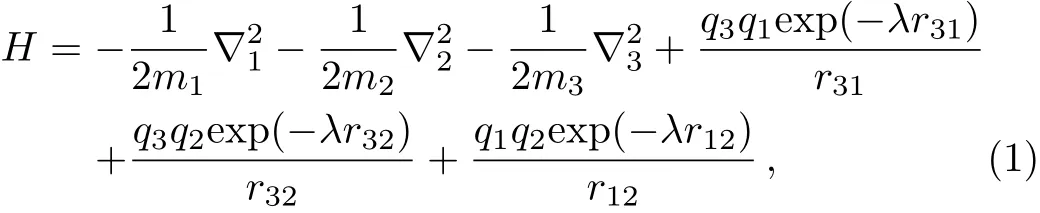
wherem1,m2,m3andq1,q2,q3are the particle masses and charges. The parameterλis known as the Debye screening parameter.The masses of proton(mp=1836.152 701),deuteron(md=3670.483 014),triton(mt=5496.921 58),muon(mµ=206.768 262)are used in the units of electron mass,mefor the systems of interest.[50−59]Applications of SCP on atomic and molecular systems have been highlighted in several articles(see Refs.[43–44,46–49,60–63]and references therein).In order to solve the Schrödinger equation for eigen-energies,one can conveniently select the Hylleraas-type wave functions involving powers of inter-particle coordinates which is suitable for the representation of molecular systems within the framework of atomic calculations and can be written as:[50,58]
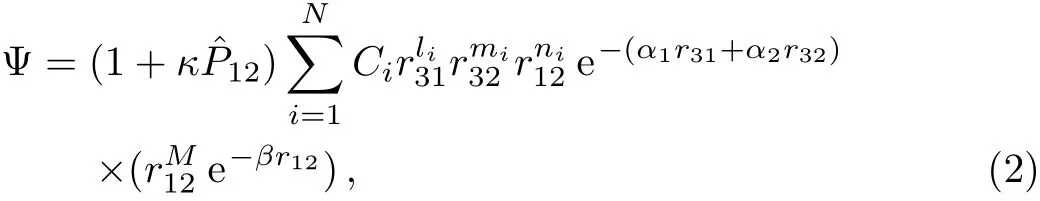
whereli,miandniare positive integers or zero,li+mi+mi≤ω,Ndenotes the number of terms in the wave functions(2)andαis the non-linear variational parameter,κ=1 forppµ,ddµ,ttµsystems,andκ=0 for HD+,HT+,DT+,tdµ,pdµ,ptµsystems.The operatoris permutation of two identical particles 1 and 2.A well-established relation for the selections ofNisN=(ω+1)(ω+2)(ω+3)/6 for non-symmetric systems,like HD+,HT+,DT+,tdµ,pdµ,ptµsystems andli≥mifor symmetric systems likeppµ,ddµ,ttµ.The internuclear motion is taken care of by the termin Eq.(2),as the relative motion of nuclei is localized near an equilibrium point and looks like a Gaussian-like function.The use of the termin the above wave function for the hydrogen-like and muonic molecular ions has been well-described in the works of Bhatia and Drachman(see Refs.[50,58]and references therein).To obtain ground state energies of the two-body systems H,D,T,pµ,dµand tµ,we diagonalize the nonrelativistic screened Hamiltonian

with the following Slater-type wave functions,

wheremis the reduced mass of nuclei and electron or muonic systems.
3 Results and Discussion
To estimate BWs,in the first step,one needs to obtain the bound states energies by solving the Schrödinger equation.In this work,we calculate the energies for the lowestJ=0 state of-like molecular ionsand muonic molecular ions tdµ,ptµ,pdµ,ppµ,ddµ,ttµ,along with their respective subsystems H,D,T,pµ,dµand tµfor the different screening parameter using the Ritz variational principal.The eigen-energies for the systems under consideration and their respective subsystems are listed in Tables 1–2 and depicted in Figs.1–3.In the tables,we present the eigen-energies for HD+,HT+,,ptµ,pdµions.The energy eigen-values for tdµ,ppµ,ddµ,ttµions as functions of screening parameters are reported in the previous articles.[5,39,43,47,49]In Table 2 and Fig.3,we have presented eigen-energies for muonic systems in muon atomic units(m.a.u.).In m.a.u.,one needs to setmp=(m1orm2)asmp/mµ,md=(m1orm2)asmd/mµ,mt=(m1orm2)asmt/mµ,andm3=1.For free-atomic systems,our findings are comparable with the available results.[43,47−52]In the tables,we have made comparison of our calculated results with the recent available data.It is also clear from the tables that our results are well converged up to quoted digits.
From this work,we found that the optimum value of(M,β)in Eq.(2)for the hydrogen molecular and muonic molecular ions are(18,9.6)and(0,0),respectively.Final results for the molecular systems are obtained usingN=560(ω=13)for the H+2-like systems,N=680(ω=14)for non-symmetric muonic molecular systems,andN=444(ω=15)for symmetric molecular systems.Results for the two-body subsystems are obtained usingNB=25 basis terms in Eq.(4).It seems from tables and figures that the proposed systems are bound but their respective subsystems are unbound in the stronger screening region and these situations lead us to find Borromean windows for the systems under study.After confirmation of the existence of Borromean states,it is necessary to determine precise critical values for the proposed threebody and two-body systems beyond which the systems would no longer support bound states.The critical values of the two-body and three-body systems are denoted respectively by
To obtain precise critical values,we extrapolate the eigen-energies in the stronger screening region for all the systems under investigation.We have also verified our critical values by fitting eigen-energies of each system with a polynomial of degree maximum up to 9.The rangeis commonly known as Borromean windows.We summarize below the rangefor the systems under study:

Figures 1–3 also show the size of windows for Borromean binding for the proposed systems in lowestJ=0 state.The critical values obtained from the present investigation are also listed in Table 3.From Table 3,it is evident that our determinations are in accord with the available results in the literature.

Table 1 Energies of the hydrogen molecular ions for selected values of screening parameters,along with the threshold values of the two-body subsystems.Results are convergent up to quoted digits.

Table 1 (Continued)
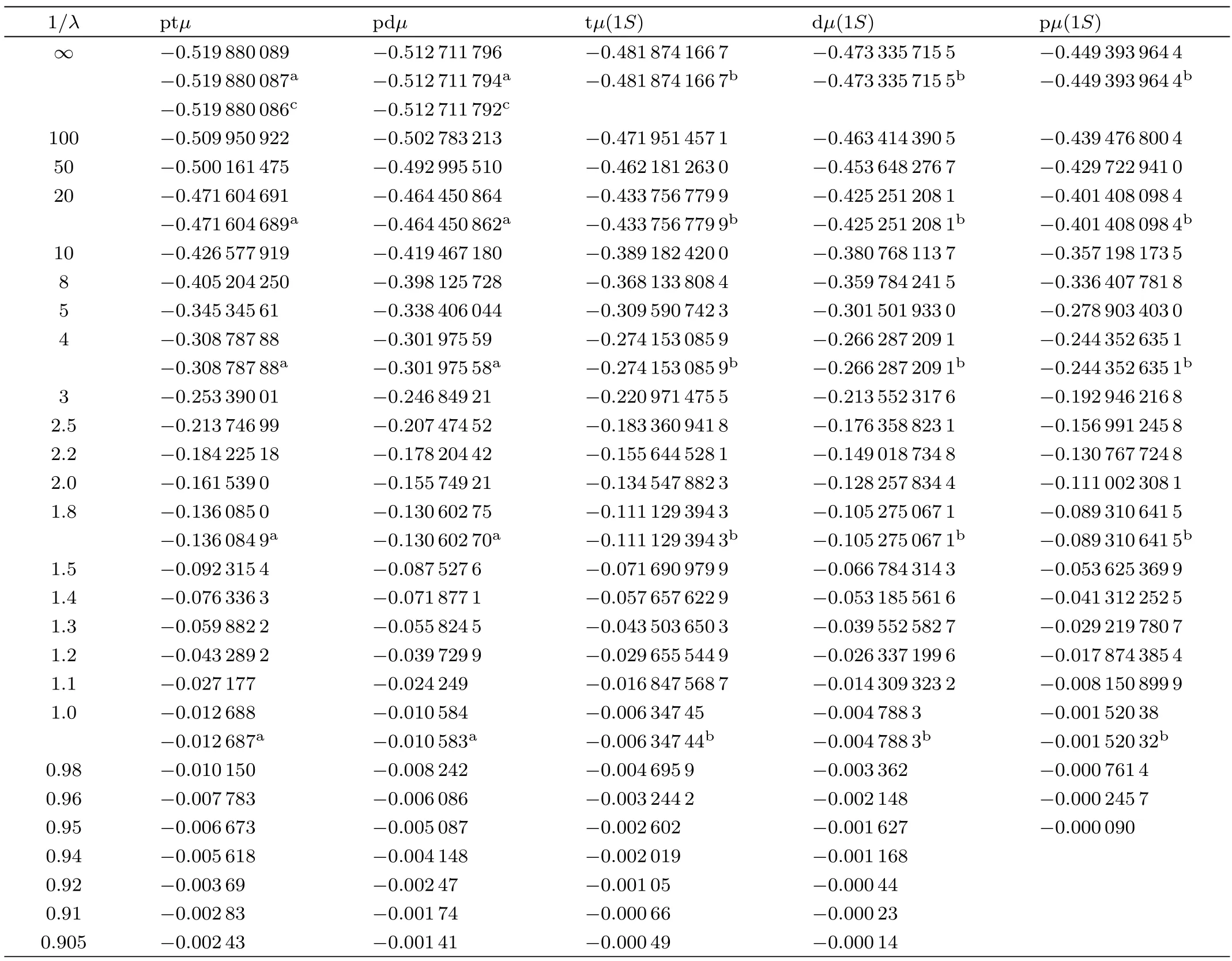
Table 2 Energies of the muonic molecular ions for selected values of screening parameters,along with the threshold values of the two-body subsystems.Results are convergent up to quoted digits.

Table 2 (Continued)
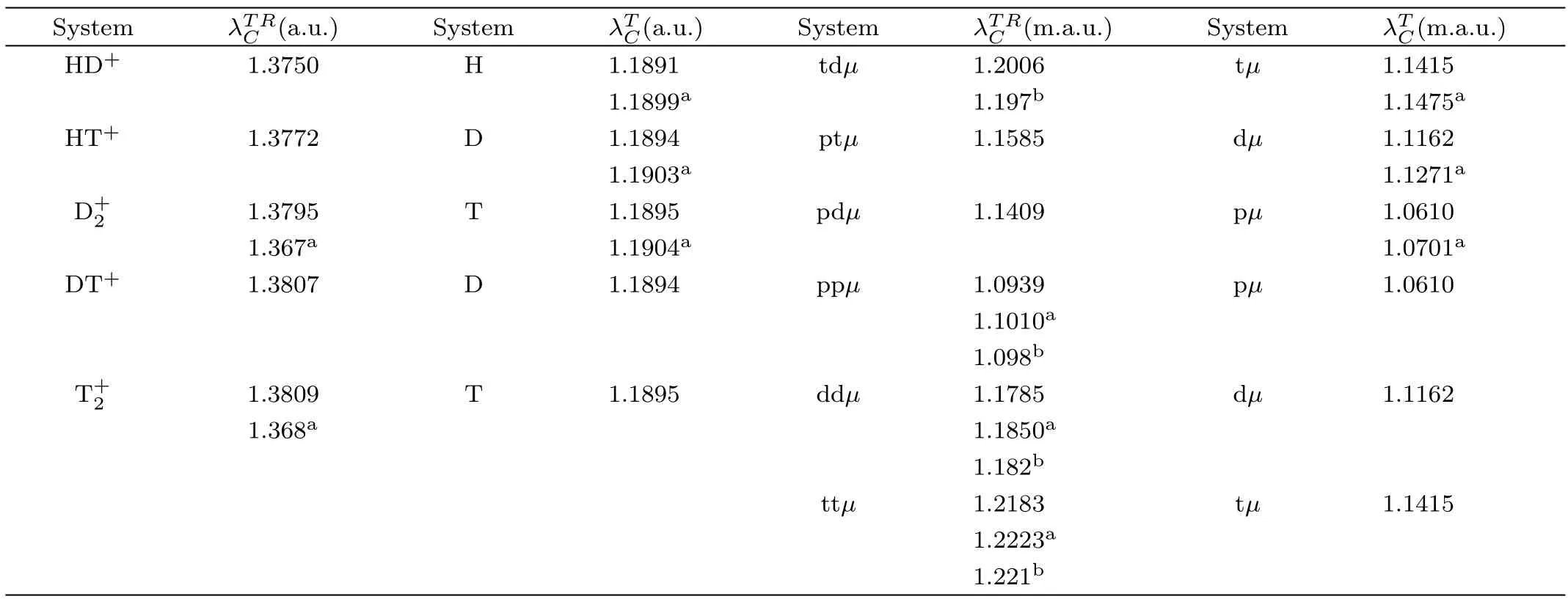
Table 3 Critical screening parameters of the hydrogen molecular ions(in a.u.)and muonic molecular ions(in m.a.u.)along with their respective two-body subsystems.

Fig.1 Energies of the hydrogen molecular ions for selected values of screening parameters,along with the threshold values of the two-body subsystems.BW indicates Borromean windows.

Fig.2 Energies of the hydrogen molecular ions for selected values of screening parameters,along with the threshold values of the two-body subsystems.BW indicates Borromean windows.
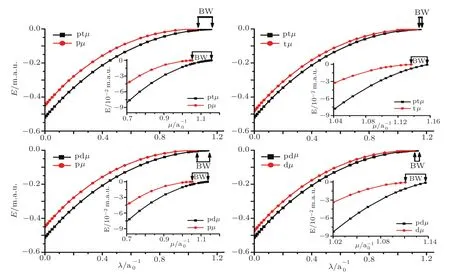
Fig.3 Energies of the muonic molecular ions for selected values of screening parameters,along with the threshold values of the two-body subsystems.BW indicates Borromean windows.
4 Summary and Conclusions
We investigate the Borromean states for-like molecular ions and the muonic molecular ions interacting with screened Coulomb(Yukawa-type)potentials using Hylleraas-type wave function within the framework of Ritz variational method.BoundJ=0 state eigen-energies of HD+,HT+,DT+,pdµ,ptµsystems for different screening parameter are presented for the first time in the literature.Borromean windows for the lowestJ=0 state of HD+,HT+,DT+,,tdµ,pdµ,ptµ,ppµ,ddµand ttµinteracting with SCP are also presented.Hope our finding will provide useful information for future studies on the Borromean binding.
[1]J.M.Richard,Few-Body Syst.38(2006)79.
[2]J.M.Richard,Phys.Rev.A 67(2003)034702.
[3]J.M.Richard and S.Fleck,Phys.Rev.Lett.73(1994)1464.
[4]M.V.Zhukov,et al.,Phys.Rep.231(1993)151.
[5]S.Dutta,J.K.Saha,S.Bhattacharyya,P.K.Mukherjee,and T.K.Mukherjee,Phys.Scr.89(2014)015401.
[6]S.Kar and Y.K.Ho,Phys.Rev.A 86(2012)014502.
[7]S.Kar and Y.K.Ho,Chem.Phys.Lett.506(2011)282.
[8]Y.Li,W.Zhang,Q.Gou,H.Song,and T.Shi,Phys.Rev.A 82(2010)022515.
[9]S.Kar and Y.K.Ho,Phys.Lett.A 368(2007)476.
[10]P.K.Mukherjee,S.Fritzsche,and B.Fricke,Phys.Lett.A 360(2006)287.
[11]J.Goy,J.M.Richard,and S.Fleck,Phys.Rev.A 52(1995)3511.
[12]V.Efimov,Phys.Lett.B 33(1970)563.
[13]F.M.Pont and P.Serra,J.Phys.A 41(2008)275303.
[14]C.Ji,Int.J.Mod.Phys.E-Nucl.Phys.25(2016)1641003.
[15]E.Braaten and H.W.Hammer,Ann.Phys.322(2007)120.
[16]A.S.Jensen,K.Riisager,and D.V.Fedorov,Rev.Mod.Phys.76(2004)215.
[17]L.H.Thomas,Phys.Rev.47(1935)903.
[18]A.Lemasson,et al.,Phys.Rev.C 82(2010)044617.
[19]Q.Gou and Y.Li,Phys.Rev.A 85(2012)012510.
[20]Y.Li,D.Huang,Q.Gou,H.Han,and T.Shi,Phys.Rev.A 84(2011)014501.
[21]C.D.Meyer,et al.,Chem.Euro.J.16(2010)12570.
[22]D.Han,S.Pal,Y.Liu,and H.Yan,Nat.Nanotechnol.5(2010)712.
[23]S.Kar and Y.K.Ho,Int.J.Quantum Chem.107(2007)353.
[24]S.Kar and Y.K.Ho,J.Phys.B:At.Mol.Opt.Phys.40(2007)1403.
[25]A.N.Sil,S.Canuto,and P.K.Mukherjee,Adv.Quantum Chem.58(2009)115.
[26]L.Liu,Y.Y.Qi,J.G.Wang,and R.K.Janev,AIP conf.Proc.1125(2009)58.
[27]S.Kar and Y.K.Ho,J.Phys.B:At.Mol.Opt.Phys.44(2011)015001.
[28]S.Kar,Phys.Rev.A 86(2012)062516.
[29]S.Kar,H.W.Li,and Z.C.Shen,J.Quant.Spectros.Radiat.Transfer 116(2013)34.
[30]S.Sen,P.Mandal,P.K.Mukherjee,and B.Fricke,Phys.Plasmas 20(2013)013505.
[31]S.Kar and Z.Jiang,At.Data Nucl.Data Tables 102(2015)42.
[32]R.K.Janev,S.B.Zhang,and J.Wang,Matter Radiat.Extrem.1(2016)237.
[33]H.W.Li and S.Kar,Phys.Plasmas 19(2012)073303.
[34]Z.Jiang,S.Kar,and Y.K.Ho,Phys.Plasmas 19(2012)033301.
[35]P.Jiang,S.Kar,and Y.Zhou,Phys.Plasmas 20(2013)012126.
[36]C.Kittel,Quantum Theory of Solids,Wiley,New York(1987).
[37]S.A.Safran and N.A.Clark,Physics of Complex and supermolecular Fluids,Wiley,New York(1987)p.65.
[38]Y.K.Ho and S.Kar,Few-Body Syst.44(2008)253.
[39]A.Ghoshal and Y.K.Ho,Int.J.Quantum Chem.111(2011)4288.
[40]F.Pont and P.Serra,Phys.Rev.A 79(2009)032508.
[41]L.Bertini,M.Mella,D.Bressanini,and G.Morosi,Phys.Rev.A 69(2004)042504.
[42]D.Bressanini,G.Morosi,L.Bertini,and M.Mella,Few-Body Syst.31(2002)199.
[43]M.Pawlak,M.Bylicki,J.K.Saha,and P.K.Mukherjee,J.Phys.B:At.Mol.Opt.Phys.42(2009)215701.
[44]M.Pawlak,M.Bylicki,and P.K.Mukherjee,J.Phys.B:At.Mol.Opt.Phys.47(2014)095701.
[45]A.G.Volosniev,D.V.Fedorov,A.S.Jensen,and N.T.Zinne,J.Phys.B:At.Mol.Opt.Phys.47(2014)185302.
[46]S.Kar and Y.K.Ho,Phys.Rev.A 75(2007)062509.
[47]S.Kar and Y.K.Ho,Eur.Phys.J.D 48(2008)157.
[48]S.Kar and Y.K.Ho,Phys.Lett.A 370(2007)306.
[49]A.Ghoshal and Y.K.Ho,J.Phys.B:At.Mol.Opt.Phys.43(2010)115007.
[50]A.K.Bhatia,Phys.Rev.A 58(1998)2787.
[51]D.H.Bailey and A.M.Frolov,J.Phys.B:At.Mol.Opt.Phys.35(2002)4287.
[52]L.Hilico,N.Billy,B.Gremaud,and D.Delande,Eur.Phys.J.D 12(2000)449.
[53]J.P.Karr and L.Hilico,J.Phys.B:At.Mol.Opt.Phys.39(2006)2095.
[54]R.E.Moss,J.Phys.B:At.Mol.Opt.Phys.32(1999)L89.
[55]J.M.Taylor,Z.C.Yan,A.Dalgarno,and J.F.Babb,Mol.Phys.97(1999)25.
[56]Z.C.Yan,J.Y.Zhang,and Y.Li,Phys.Rev.A 67(2003)062504.
[57]A.M.Frolov,J.Phys.B:At.Mol.Opt.Phys.35(2002)L331.
[58]A.K.Bhatia and R.J.Drachman,Can.J.Phys.79(2001)1149.
[59]A.M.Frolov,Eur.Phys.J.D 66(2012)212.
[60]S.Kang,J.He,N.Xu,and C.Y.Cheng,Commun.Theor.Phys.62(2014)881.
[61]S.Kar,Y.S.Wang,W.Q.Li,and X.D.Sun,Int.J.Quantum Chem.115(2015)1573.
[62]S.Kar,Y.S.Wang,Y.Wang,and Z.Jiang,Phys.Plasmas 23(2016)082119.
[63]Y.K.Ho and S.Kar,Chin.J.Phys.53(2016)574.
猜你喜欢
杂志排行
Communications in Theoretical Physics的其它文章
- Anharmonic Properties of Aluminum from Direct Free Energy Interpolation Method∗
- Effects of Interfaces on Dynamics in Micro-Fluidic Devices:Slip-Boundaries’Impact on Rotation Characteristics of Polar Liquid Film Motors∗
- Controlling Thermodynamic Properties of Ferromagnetic Group-IV Graphene-Like Nanosheets by Dilute Charged Impurity
- Elastic Deformation Analysis on MHD Viscous Dissipative Flow of Viscoelastic Fluid:An Exact Approach
- Entropy Generation Analysis in Convective Ferromagnetic Nano Blood Flow Through a Composite Stenosed Arteries with Permeable Wall
- Isotopic Effects on Stereodynamics of the C++H2→ CH++H Reaction∗
