结构力学位移法基本思路和基本未知量的确定

黄 志 刚

(湖南文理学院土木建筑工程学院,湖南 常德 415000)

0 引言

《结构力学》课程是土建、水利、力学等专业的一门重要的学科基础课[1]，具有理论性强和灵活性大的特点，搞好它的教与学是培养学生分析和计算能力的关键，它对新的人才培养模式的实现起着十分重要的作用。而超静定结构的内力和变形分析是其中很重要的一项内容。

力法和位移法是分析超静定结构的两种基本方法[2]。力法是在19世纪末就已经应用于各种超静定结构的分析。随后，由于钢筋混凝土结构的出现，大量高次超静定刚架逐渐增多，如果仍用力法计算将十分麻烦。于是20世纪初又在力法的基础上建立了位移法。

力法的基本思路是先解除超静定结构上的多余约束，代之以多余未知力，以多余未知力为基本未知量，一般取静定结构为基本结构进行计算。利用位移协调条件建立力法基本方程，求出多余未知力，然后进一步求出结构的内力。位移法的基本思路与力法相反。位移法是以结构的结点位移作为基本未知量，以一组单跨超静定梁为计算的基本单元。先设法确定出单根杆件的杆端内力，用杆端位移来表示，这些杆端位移应与其所在结点的其他杆端位移相协调。然后用力的平衡条件建立位移法基本方程，确定出未知的结点位移，从而进一步求出整个结构的内力。

由于位移法思路的独特性，在地方性应用型本科院校的《结构力学》课程教学过程中，学生学习这块内容时，往往感到非常迷惑，倍感费劲。加之，当前《结构力学》教材中所给出的确定位移法基本未知量的方法，在文字叙述上不够严谨，定义不够明确，容易让学生在学习过程中产生混淆和导致错误结论[3]。因此，对位移法的基本思路和基本未知量的确定进行探析和归纳很有现实意义。

1 位移法的基本思路

位移法是求解超静定结构的另一种基本方法，与力法相比，位移法的解题过程比较规范，便于编制计算机程序，但基本思路相对难理解一些，以下以图1a)所示的刚架为例说明位移法的基本思路。

在荷载作用下，刚架产生的变形如图1a)中虚线所示，设结点B的转角为Δ1，根据变形协调条件可知，汇交于结点B的BA杆和BC杆两杆端也应有同样的转角Δ1。为了简化计算，在受弯杆件中，忽略杆件的轴线变形和剪切变形的影响，假设弯曲变形很小，因此可以假定结构变形后受弯杆件的两端之间的距离不变。根据这些假定，B结点就只有角位移而没有线位移。如果能知道B点的角位移Δ1，就可以求出刚架的内力。

下面来设法求出B点的角位移Δ1。假设在B点处加上一个附加刚臂，这个附加刚臂约束了B点的转动。原结构就变成了两个相互独立的单跨超静定梁，把它称为位移法的基本结构，如图1b)所示。第一步在基本结构上加荷载FP，只有梁BC发生变形，B点没有角位移，在附加刚臂中产生了一个约束反力矩F1P。第二步使基本结构的B点转动Δ1，同时附加刚臂处会产生一个反力矩F11。

将第一步和第二步的结果叠加，得到的基本结构的变形与原结构一致。注意到原结构在B点并没有附加刚臂，也不存在约束反力矩，所以：

F11+F1P=0

(1)

这里的F11是基本结构在B点发生转角Δ1时，产生在附加刚臂的反力矩。用k11表示基本结构在B点处发生单位转角Δ1=1时，产生在附加刚臂中的反力矩，则式(1)可以写成：

k11Δ1+F1P=0

(2)

式(2)称为位移法基本方程。k11，F1P可以用力法(后续可以通过形常数和载常数)确定，进而求出原结构的全部内力。

由以上分析可知，用位移法求解结构内力的要点是：

1)位移法的基本未知量是结构的独立结点位移，如图1a)中的B点的角位移。

2)位移法以单根杆件作为计算基础。通过附加约束，把复杂结构的内力计算拆分为三类基本杆件的内力状况的叠加。三类基本杆件都是等截面杆件，如图2所示。

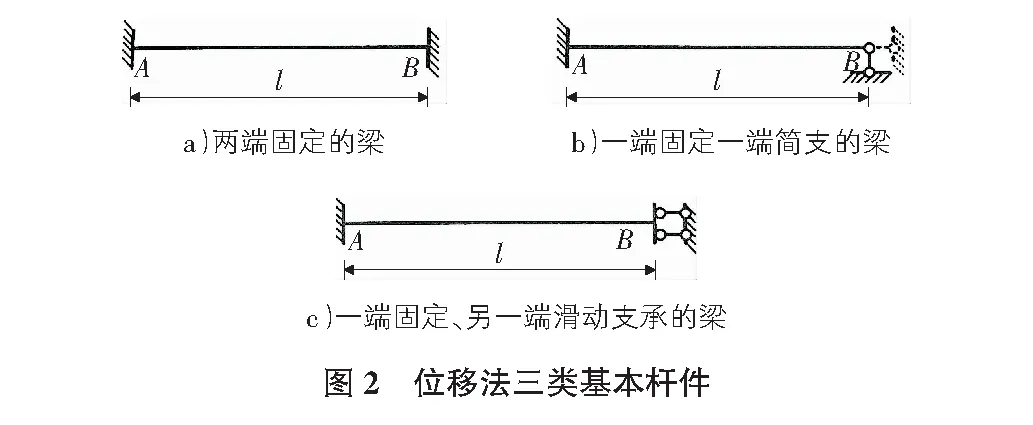
3)基本结构的选取：通过在杆端附件约束，限制结点位移(被约束住的位移即为基本未知量)，把结构所有杆件转化为三类基本杆件。此时附加了约束的超静定结构即为基本结构。

4)位移法的基本方程是平衡方程，如式(2)是B点的力矩平衡方程。位移法基本方程的物理意义是基本结构在结点独立位移和各种因素(荷载、支座位移、温度变化等)的共同作用下，附加约束上的反力等于零。用数学式子表达的一般形式为：

(3)

其中，kij为基本结构在单位位移Δj=1单独作用时，在第i个附加约束上产生的反力；FiP称为自由项，它表示荷载单独作用时，在第i个附加约束上产生的反力，故又称为荷载项；FiP,Fic,Fit分别为基本结构在荷载、支座移动和温度变化等因素作用时，在第i个附加约束上产生的反力。所有系数和自由项均取与所设基本未知量Δj的方向一致为正，反之则为负。

5)内力计算：将基本未知量求出后，最后的弯矩图等于基本结构分别在荷载等其他因素和基本未知量单独作用下的弯矩图相叠加，即:

(4)

与力法不同，位移法的基本结构是超静定结构，荷载、支座位移、温度变化等因素都有可能引起内力。

2 位移法的基本未知量

位移法是以结点位移为基本未知量，基本未知量的数目等于独立结点角位移数目加上独立线位移数目。

独立结点角位移数目的确定比较简单：为使结点不发生角位移，需要在结点上施加附加刚臂，则附加的刚臂数目就是独立结点角位移的数目，它等于全部刚结点和半铰结点的结点数目。但需要注意的是：铰结点的角位移不取为基本未知量；刚度无穷大的梁端若不发生转角，则与刚度无穷大的杆相连的刚结点的转角也不取为基本未知量。例如图5a)所示，A为刚结点，B为半铰结点，故有两个独立角位移；而图5b)中B为刚结点，A为铰结点，故只取B点转角为独立角位移；而图5c)中AB杆刚度无穷大，此时φA=φB=0，基本未知量只有一个线位移Δ。

独立的结点线位移数目的确定较复杂，基本可以根据以下原则而确定：

1)附加链杆法(最稳妥的方法)。在结点施加附加链杆，使其不发生线位移，则附加链杆数目即为独立结点线位移数目。应用此法时需注意，剪力静定杆(即自由端、滑动支承端或滚轴支承端的与杆轴垂直方向)的线位移不取作基本未知量。

2)铰化法(应慎重使用)。将刚架中刚结点(包括固定端)全部改为铰结点，成为铰接体系，其自由度数目即为独立线位移数目。

利用这种方法时应注意，它只适合于杆件的边界端是固定端、铰支端和垂直杆轴的滚轴支承端。若边界是自由端、滑动支承端和沿杆轴方向的滚轴支承端，利用此方法会得出错误的结论。如图6a)，图6b)表示两种不同的刚架，铰化后均为图7所示的铰接体系，其自由度为2，而原刚架独立结点线位移数为1。这是因为D结点的线位移为垂直于杆轴方向，属于不独立的结点位移，不应取作基本未知量。

确定位移法的基本未知量数目时还应注意：角位移和线位移均不包括静定部分。

3 结语

位移法既是《结构力学》课程教学的一个重点，又是一个难点。但由于位移法解题思路的独特性，较力法而言，相对难理解一些，让很多学生摸不着头脑。实践经验证明，若能很好地掌握以上归纳总结，并进行系统化练习，那学生领会位移法，并将其运用到工程实际将不再是很困难的事。

[1] 李国华,罗 健,董 军,等.结构力学教学方法研究[J].高等建筑教育,2012,21(1):81-83.

[2] 龙驭球,包世华.结构力学Ⅰ——基本教程[M].第2版.北京:高等教育出版社,2006.

[3] 唐雪松.一种新的判别位移法基本未知量的方法[J].力学与实践,1999(2):71-72.