一种机电集成锻造操作机钳杆永磁传动旋转装置

张鸿飞 ，贾 ，赵晓峰 ，姚 鹤

（1.兰州兰石能源装备工程研究院有限公司，甘肃 兰州 730050；2.甘肃省金属塑性成型装备智能控制重点实验室，甘肃 兰州 730050）

锻造操作机是锻造行业自动化生产过程中不可或缺的辅助操作装置，在提高生产率、改善生产条件、降低劳动强度、提高锻造质量方面非常重要[1-2]。目前传统的锻造操作机主要是全液压型驱动控制，其响应速度较慢，而且锻造操作机钳杆旋转部分传动机构采用液压马达、机械星型齿轮减速器、机械齿轮传动形式，如图1所示。由于机械齿轮传递效率高，传动比稳定，可传递转矩大等优点，广泛应用于机械工业的各个领域[3-5]，但是机械齿轮传动中主、从动轮轮齿直接接触，容易发生疲劳断裂、摩擦损耗，产生振动、冲击、噪声及需要良好的润滑；而且由于液压马达自身的特殊性，在启动运行时不稳定、工作运行时有冲击、振动、漏油，容易造成环境污染、维修不便，且进口价格昂贵[6]。目前国内外学者对锻造操作机的研究主要在其机械结构优化分析、控制系统、疲劳[7-9]等方面，而对其传动形式研究很少。

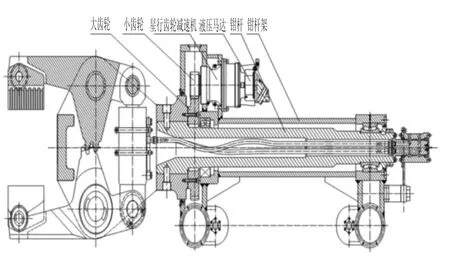
图1 传统钳杆旋转结构装置

基于以上背景，本文提出了一种机电集成锻造操作机钳杆永磁传动旋转装置，如图2所示。它集磁场调制型磁齿轮与伺服电机控制的优点于一体，其控制精度、响应速度、单位体积力密度可与传统液压马达、机械星型齿轮减速器组成的传动机构相媲美[10]。

图2 机电集成钳杆永磁传动旋转结构装置

1 三维模型

基于SolidWorks，按表1建立了一种机电集成锻造操作机钳杆永磁传动旋转装置的结构简化模型，如图3所示。主要由伺服电机、内转子（内转子轴及其外表面永磁体）、调磁环、外转子（小齿轮轴及其内表面永磁体）、啮合的大小机械齿轮、钳杆构成。内转子、调磁环、外转子构成第一级传动；小齿轮轴、大齿轮、钳杆构成第二级传动。

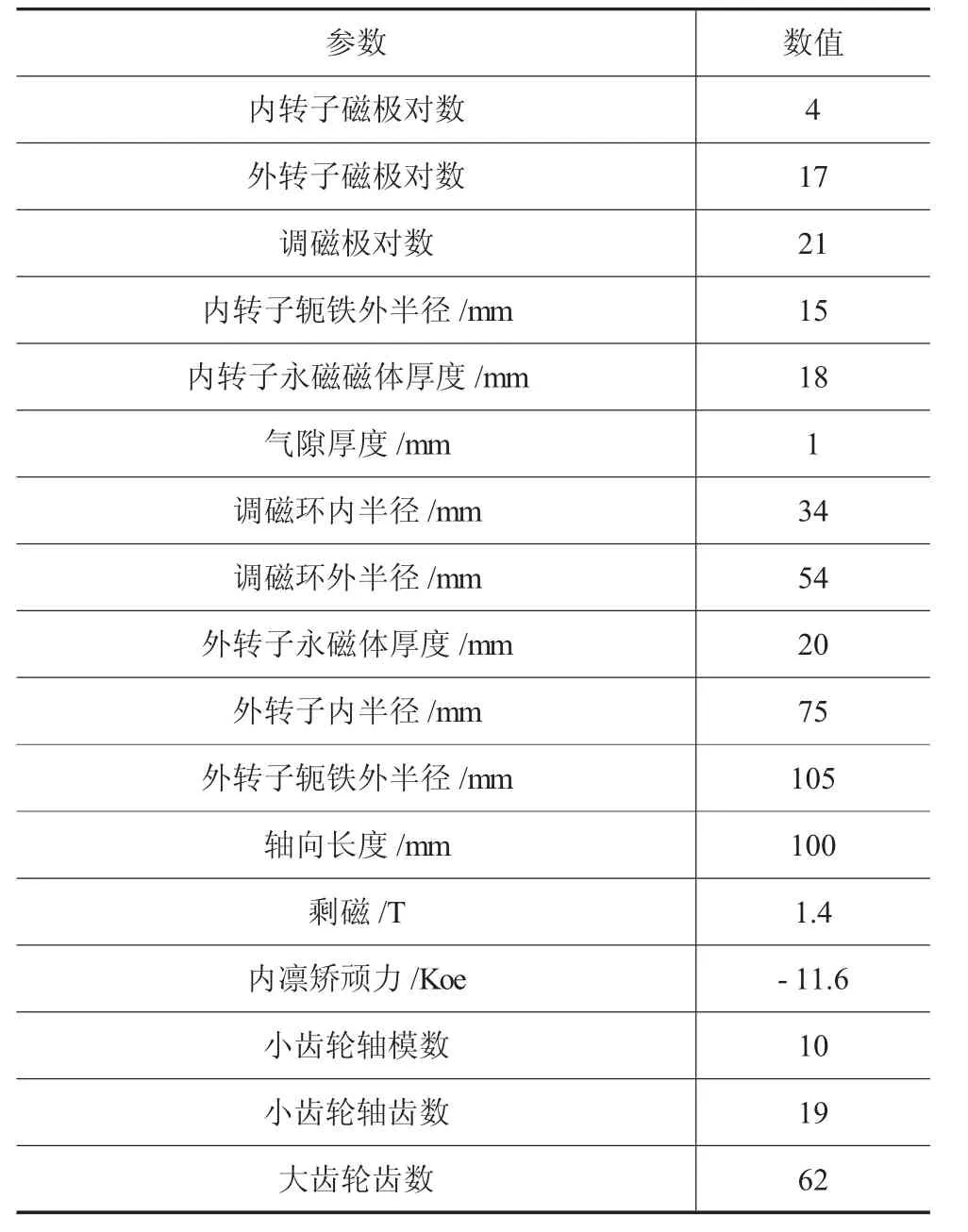
表1 主要参数

图3 三维结构模型

2 工作原理

如图3所示，机电集成锻造操作机钳杆永磁传动旋转装置具有两级减速机构，即小齿轮轴内部集成的磁场调制型磁齿轮，构成为第一级传动；小齿轮轴与大齿轮啮合传动，构成第二级传动；内转子轴外表面间隔布置有极对数为p1的N极、S极永磁体，小齿轮轴内表面间隔布置有极对数为p2的N极、S极永磁体，调磁环由导磁和非导磁材料组成环形，导磁、非导磁极对数均为p1+p2。

当伺服电机驱动内转子轴做旋转运动的同时，内转子轴外表面上的永磁体在气隙1内产生主谐波次数为N1的旋转磁场，正好与内转子轴外表面永磁体极对数吻合，经调磁环磁场调制后，在气隙2内产生主谐波次数为N2的旋转磁场，正好和小齿轮轴内表面永磁体极对数吻合，实现其等磁极耦合传动，从而使得小齿轮轴做回转运动，实现其第一级减速传动；当小齿轮轴做回转运动的同时，小齿轮轴的轮齿与大齿轮轮齿做啮合运动，进而驱动钳杆做旋转运动，实现其第二级减速传动。

机电集成锻造操作机钳杆永磁传动旋转装置的第一、第二级传动的减速比及承载能力可分别调节内转子轴外表面永磁体极对数、小齿轮轴内表面永磁体极对数、径向厚度、轴向长度、永磁体剩磁等参数以及小齿轮轴、大齿轮轮齿数等参数实现，其转速可通过伺服电机调节控制，实现其正反转，从而实现钳杆低速大扭矩传输，实现钳杆的回转夹持功能。

3 有限元分析法

3.1 有限元模型

机电集成锻造操作机钳杆永磁传动旋转装置的第一级转矩特性主要依赖于小齿轮轴内部集成的磁场调制型磁齿轮传动机构，因此采用有限元法分析其转矩特性时，只需单独建立并分析小齿轮轴及其内部结构的有限元2D模型即可。基于Ansoft Maxwell电磁场有限元分析软件，建立了如图4所示的有限元分析模型，包括结构2D模型、初始网格划分模型、磁力线分部模型。

从图4a初始网格剖分上看，考虑到气隙部分的磁阻比永磁体和小齿轮轴大，所以气隙1、2部分的网格划分较密，内转子轴上的永磁体与内转子轴的网格单元共用边界节点，同样小齿轮轴内表面上的永磁体与小齿轮轴的网格单元也共用边界节点，且装置的内、外转子回转过程中内转子、外转子单元刚性转动，气隙1、2中间位置处为非节点共用区，机构回转过程中边界节点之间通过插值实现内转子与调磁环之间磁感应强度的计算，虽然插值计算会带来一定的误差，但气隙网格较密，对整体计算精度影响不大。

采用有限元方法得到机电集成锻造操作机钳杆永磁传动旋转装置的磁力线分布如图4b所示。机电集成锻造操作机钳杆永磁传动旋转装置的磁力线有两种情况：①内转子、外转子传动部分相邻永磁体边缘接触部分的磁力线就近闭合；②内转子轴外表面永磁体产生的旋转磁场的磁力线经调磁环、小齿轮轴内表面永磁体、小齿轮轴形成回路，使得内转子、调磁环及外转子间存在耦合磁场，实现耦合传动。

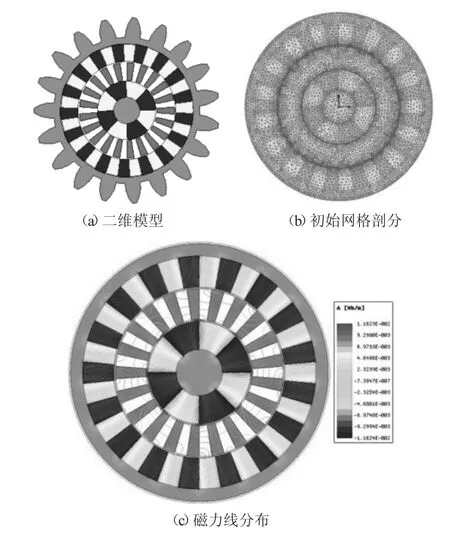
图4 二维有限元模型

3.2 磁通密度及空间谐波

内转子与外转子间的相对旋转角度为π/8时，利用有限元法得到气隙1、2中间位置处的径向、切向磁通密度，如图5所示。由图可知气隙1、2的径向和切向气隙磁密经由调磁环磁场调制后，基本成正弦规律曲线变化，且气隙2的磁密较气隙1更密，幅值更大。

对气隙1、2中间位置处的径向磁通密度进行傅里叶变换即得到其所对应的空间谐波次数，如图6所示。由图可知气隙1、2的空间主谐波次数正好与所设计的内转子轴外表面永磁体极对数和小齿轮轴内表面永磁体极对数吻合，说明经调磁环调制后，内外转子之间可以实现等磁极耦合传动，除主谐波外，还存在着其他谐波分量。

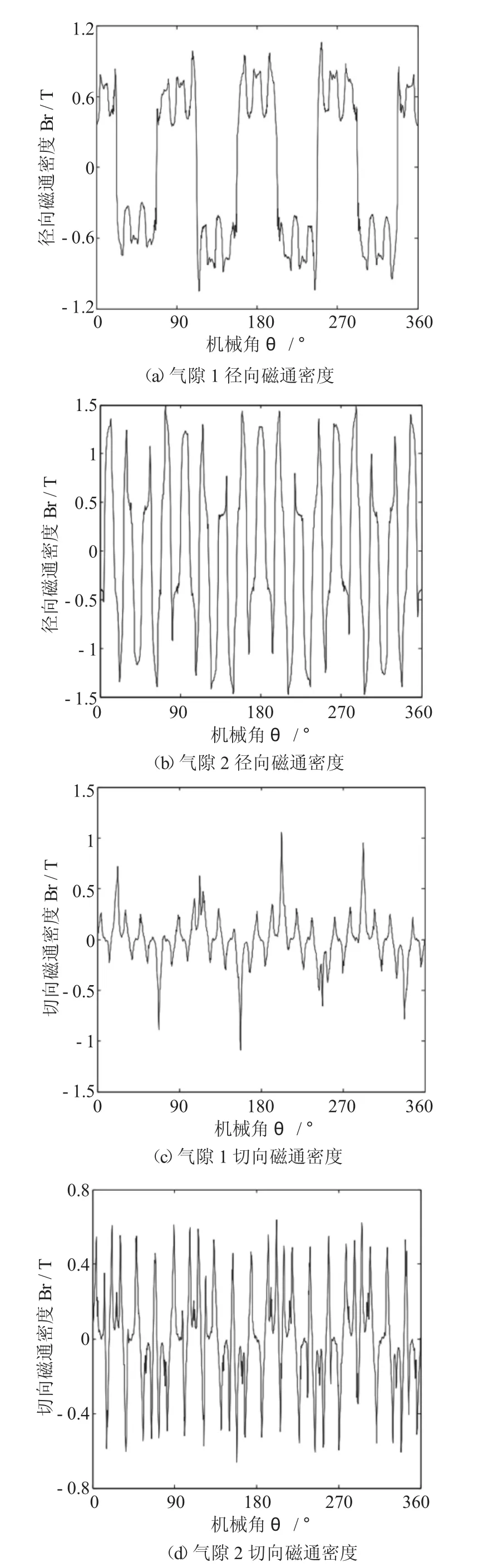
图5 气隙磁通密度

图6 气隙空间谐波次数

3.2 静态转矩特性

基于Ansoft Maxwell的magnetostatic分析，小齿轮轴（外转子）固定不动，内转子缓慢线性地转过一定的机械角度（一个周期），即可得出外转子的静态转矩曲线；内转子固定，外转子缓慢线性地转过一定机械角度，也可得出内转子的静态转矩特性曲线，机电集成锻造操作机钳杆永磁传动旋转装置的第一级传动的静态转矩曲线，如图7所示。

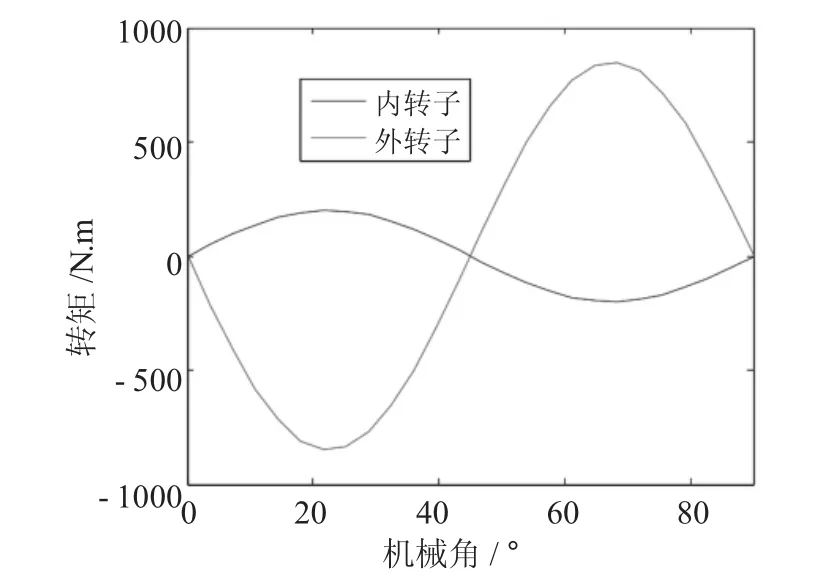
图7 内外转子静态转矩

机电集成锻造操作机钳杆永磁传动旋转装置在运行过程中，其驱动能力取决于内转子、外转子的最大静态转矩，当小齿轮轴（外转子）的负载大于外转子所承受的最大静态转矩的时候，内、外转子之间将失去磁耦合力作用，小齿轮轴（外转子）静止不动，伺服电机驱动内转子做振荡衰减运动，从而实现钳杆装置的过载自我保护。

3.3 动态转矩特性

在带负载稳定运行仿真过程中，以内转子为输入，小齿轮轴（外转子）为输出，基于Ansoft Maxwell的Transient分析，得出了机电集成锻造操作机钳杆永磁传动旋转装置内、外转子动态转矩特性曲线，如图8所示。

图8 动态转矩

由图8可知，机电集成锻造操作机钳杆永磁传动旋转装置的内、外转子稳态运行过程中，其转矩具有微小波动特性，且其所传递的转矩符合传动比4.25。由于仿真过程中外转子的机械特性，如转动惯量、摩擦阻尼未加考虑，导致稳态运行时，外转子的动态转矩波动较大。

3.4 启动特性

在空载启动仿真过程中，以内转子为输入，小齿轮轴（外转子）为输出。内转子轴在伺服电机驱动下，以85rpm的旋转转速驱动小齿轮轴旋转，仿真时间为500ms，基于Ansoft Maxwell的Transient分析，机电集成锻造操作机钳杆永磁传动旋转装置由启动到稳态运行过程中，内转子、小齿轮轴（外转子）的转速、转矩如图9、图10所示。

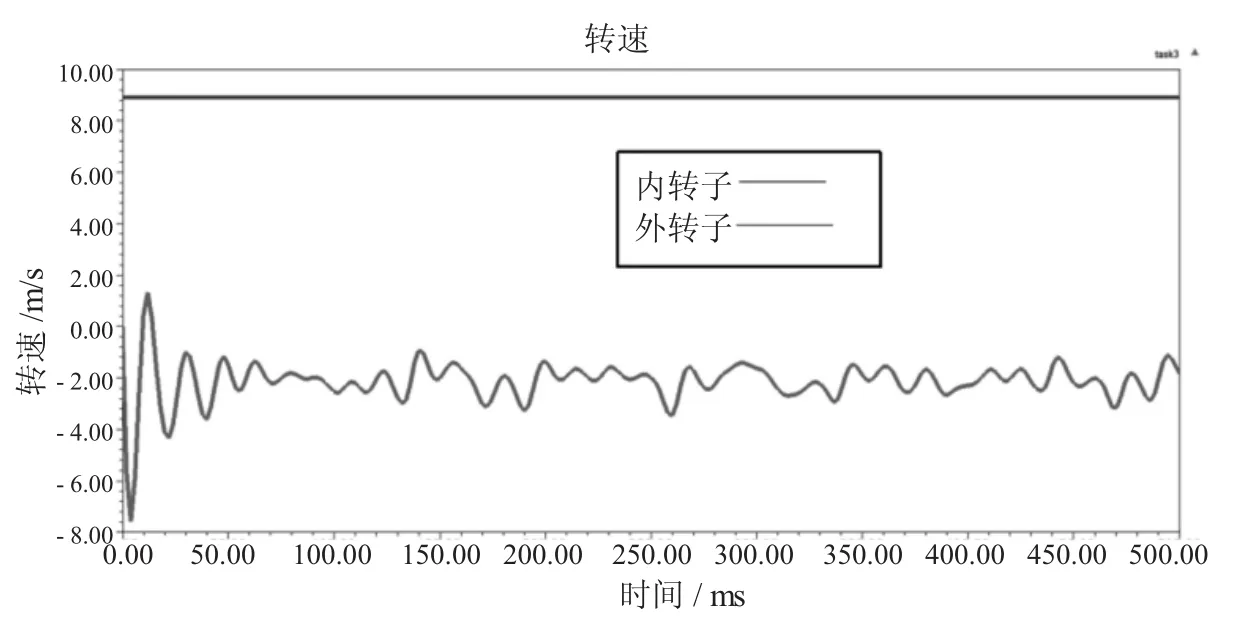
图9 启动转速

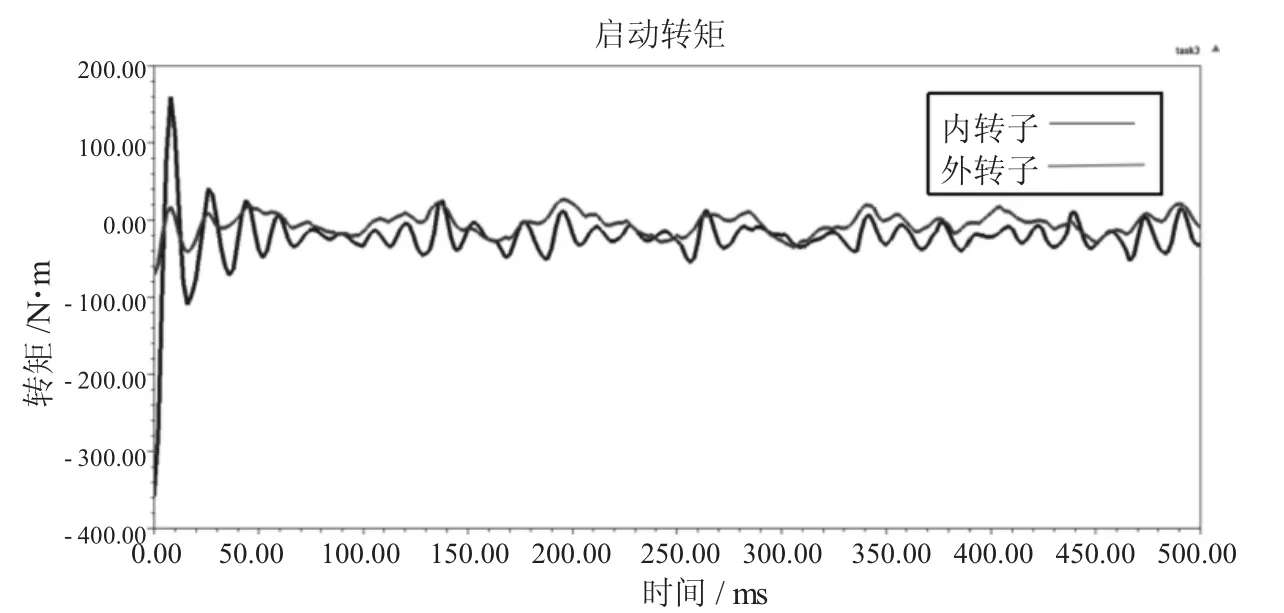
图10 启动转矩

由图9可知，机电集成锻造操作机钳杆永磁传动旋转装置的内转子通过磁耦合作用驱动小齿轮轴（外转子）旋转，且其转速传动比符合4.25。小齿轮轴（外转子）在内转子驱动下外转子速度由开始的较大波动到稳定运行，其速仍然具有微小波动，小齿轮轴（外转子）旋转速度由暂态进入稳态的运行时间很短。

由图10可知，机电集成锻造操作机钳杆永磁传动旋转装置的内、外转子转矩启动后由暂态振荡进入到稳态，由于空载起步，所以内、外转子转矩绕坐标轴原点零位置上下波动。

4 结论

（1）机电集成锻造操作机钳杆永磁传动旋转装置的气隙1、2内的磁场主谐波次数与其对应的内、外转子磁极对数吻合，且各气隙内磁场为包含主谐波在内的多次谐波叠加，从而揭示了其磁耦合工作机理。

（2）基于Ansoft Maxwell，利用麦克斯韦应力张量法，得出的内、外转子静态转矩呈正弦规律变化，且内、外转子的最大静态转矩分别为200N·m和850N·m。

（3）机电集成锻造操作机钳杆永磁传动旋转装置的内、外转子在工作过程中其转速、转矩均具有微小波动，且其工作状态由暂态到稳定时间很短。

[1]张营杰，卫凌云，牛 勇，等.锻造操作机发展现状与研究方向[J].锻压装备与制造技术，2012，47（2）：11-14.

[2]王凤喜.锻造液压机与操作机的发展[J].锻压装备与制造技术，1998，33（6）：3-5.

[3]赵 韩，吴其林，黄 康，等.国内齿轮研究现状及问题研究[J].机械工程学报，2013，19：11-20.

[4]王丽娟，黄清世，邹 雯.齿轮发展研究综述[J].机械研究与应用，2008，（1）：17-18.

[5]鄂中凯.齿轮传动设计[M].北京：机械工业出版社，1985：1-53.

[6]秦春魁.液压马达起动及低速力矩特性综述[J].西安冶金建筑学院学报，1979，（Z1）：115-126.

[7]YaJunFan，AnLeMu，TaoMa.Design and control of a point absorber wave energy converter with an open loop hydraulic transmission[J].Energy Conversionand Management，2016.

[8]郝立文.大型锻造压机操作系统的发展方向[J].黑龙江科技信息，2016，（23）：161-162.

[9]陈高杰.锻造操作机钳臂结构疲劳分析[D].大连：大连理工大学，2009.

[10]AtallahK，Howe D.A Novel High-Performance Magnetic Gear[J].IEEE Transactions on Magnetics，2001，37（4）：2844-2846.