茶叶杀青机电磁加热过程模拟及关键参数设计*

詹星星，赵章风，钟 江，乔 欣

(浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室，浙江 杭州310014)

0 引 言

滚筒杀青机是市场上使用最广泛的杀青设备，但这些设备加热方式预热时间长、能源利用率低、温控性能差[1]，不仅影响茶叶的杀青质量，同时造成资源浪费。电磁加热技术[2]作为金属热处理领域广泛使用的加热技术，利用电磁加热可节能30%以上，并且热能的转化率可达90%以上[3]。但电磁加热涉及电磁场与温度场的耦合，通过求解描述电磁场分布的麦克斯韦方程组[4]十分困难，并且在加热过程中，导体的磁导率、电导率和比热容都会随着温度的变化而变化，这都给分析温度场都来很多困难，因此在实际设计时，需要采用大量试验来得到所需工艺参数。

目前，国内外还没有学者利用数值模拟技术对电磁杀青机进行参数设计。陈天翔[5]利用有限元分析软件对钢管感应加热过程进行了模拟研究，分析了电流频率对钢管感应加热过程中钢管内外壁的温差和加热效率的影响，得到了感应加热频率选择依据，但未对其他关键参数展开分析。易小开等[6]对厚壁管道中频感应加热过程的磁-热耦合进行了数值模拟，研究了电流频率、电流强度以及线圈与管道之间的空气间隙等主要参数对管道加热效率的影响，得到了提高加热效率的参数优化方案。

笔者利用ANSYS对电磁杀青机滚筒加热过程进行模拟，分析各因素对滚筒温升的影响。

1 电磁加热集肤效应与能量参数

电磁加热原理[7]如图1所示。

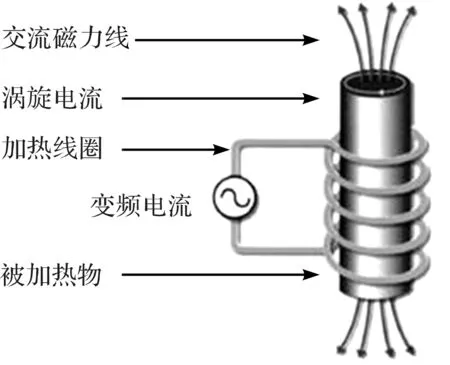
图1 电磁加热原理图

工频交流电通过电磁加热器整流成直流，然后再逆变为高频交流，交流电经感应线圈产生交变磁场。由于金属导体置于交变磁场中，在其中将产生涡流，进而产生焦耳损耗，继而产生大量热量，达到加热目的。

当交流电流通过导体时，会产生集肤效应[8]。工程上规定导体某一深度Δ处的电流密度为其表面电流密度的1/e=0.368时，这个深度Δ就是电流透入深度，其值可按下式计算[9]：

(1)

式中：Δ—电流透入深度，cm；ρ—导体电阻率，Ω·cm；μr—相对磁导率；f—电流频率，Hz。

在一定时间内滚筒的温升速度，取决于单位时间内向滚筒单位表面积所提供的能量，即比功率P0，比功率可用下式表示[10]：

(2)

式中：K—决定于感应线圈和滚筒几何尺寸的系数；I—感应线圈中的电流，A；ρ—滚筒材料的电阻率，Ω·cm；μ—滚筒材料的导磁率，H/m；f—电流频率，Hz。

电磁杀青中滚筒的最终温度还与加热时间有关，在一定的比功率下，加热时间越长，滚筒的最终温度越高，通过改变加热比功率的大小和加热时间的长短，就可以调节滚筒的加热速度和最终温度。

2 电磁杀青滚筒加热过程数值模拟

2.1 电磁杀青机基本结构

在传统电热式滚筒杀青机的基础上，电磁杀青机是将环绕在筒体表面的电热管更换为感应线圈，按照“高温杀青，先高后低”的工艺原则，对各段滚筒温度进行单独控制，其基本结构由滚筒筒体、加热线圈、传动装置、排湿装置、支撑支架、进料、出料装置等部分组成，电磁杀青机结构示意图如图2所示。

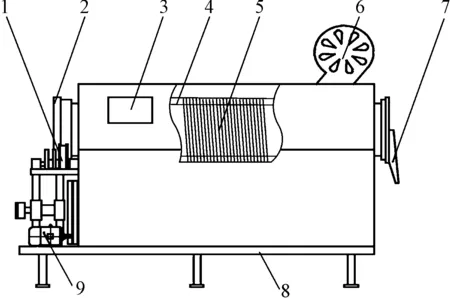
图2 电磁杀青机结构示意图 1—拖轮；2—进料口；3—控制台；4—滚筒；5—线圈；6—排湿装置；7—出料口；8—支撑支架；9—传动电机

滚筒两端由定位拖轮支撑，工作时支架底部的电机通过传动装置驱动拖轮，再由拖轮通过摩擦带动滚筒旋转。

2.2 电磁加热数值模拟分析流程

本研究的耦合场分析采用载荷传递法中的物理环境法[11]，具体流程如图3所示。

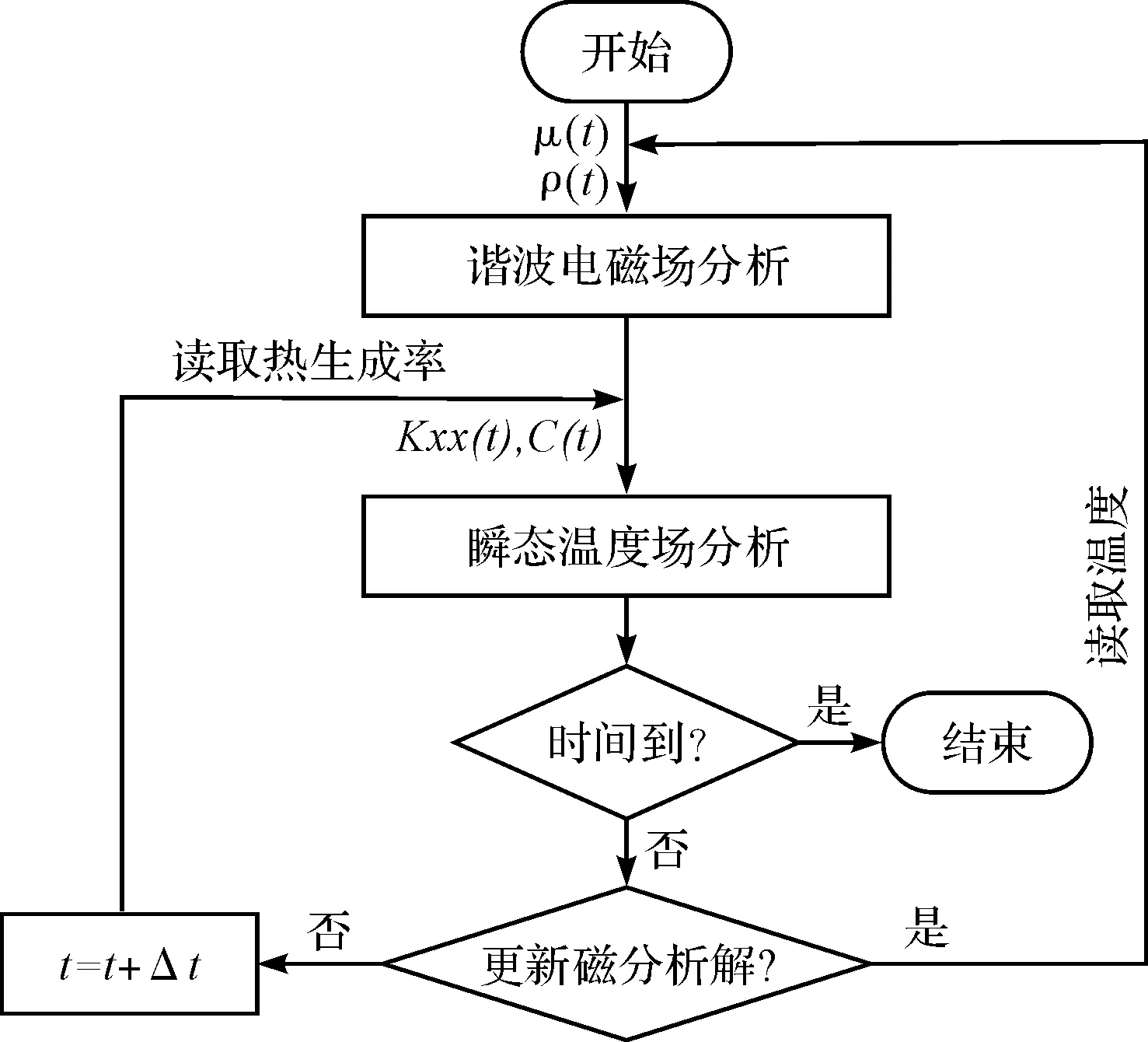
图3 电磁加热过程分析流程

本研究首先进行谐波电磁场分析，再进行瞬态温度场分析，根据循环次数的设置判断是否更新磁分析，将新的材料物理场参数代入下一次分析，如此循环进行磁-热耦合分析计算[12]。

数值模拟以电磁杀青机滚筒为对象，滚筒材料为Q235钢，其基本尺寸参数如表1所示。

表1 滚筒尺寸参数

物理参数如表2所示。

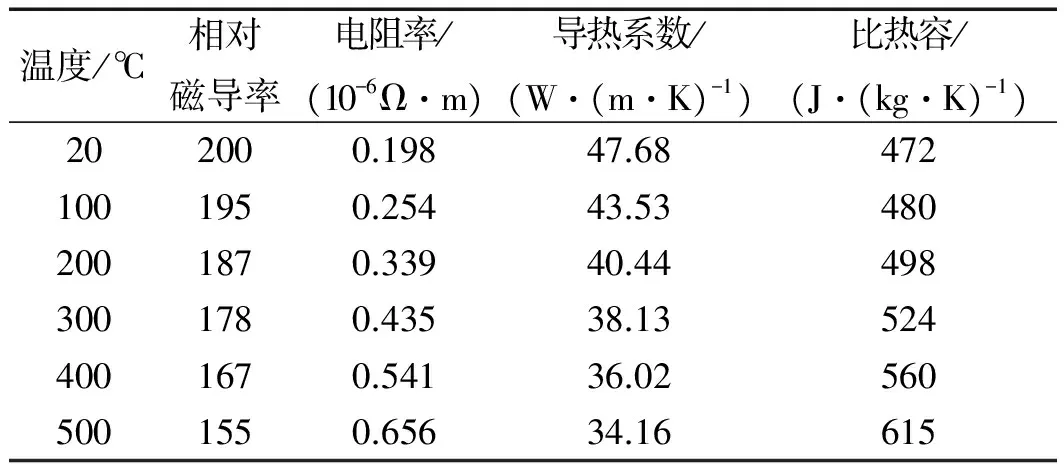
表2 Q235钢物理参数

由于集肤效应，在实际应用中，线圈截面为空心方形管，空心部分通冷却水，其截面形状如图4所示。

图4 感应线圈截面图

另外由于圆环效应和邻近效应的影响，线圈中的电流会高度集中于线圈内侧透入深度内，线圈的有效截面积就是线圈的宽度与电流透入深度的乘积，因此在构建线圈模型时，本研究只取线圈内侧进行建模，在其上施加电流密度载荷，可由通入线圈的电流除以有效截面积得到，即假设电流只在线圈内侧透入深度内流过，其余部分没有电流。为了减少计算时间，本研究采用单匝线圈代替螺线管线圈进行仿真分析，简化后的模型如图5所示。

图5 滚筒电磁加热仿真模型

2.3 数值模拟结果

本研究在建立完有限元模型后，对滚筒电磁加热过程进行数值模拟，模拟结果如图6所示。

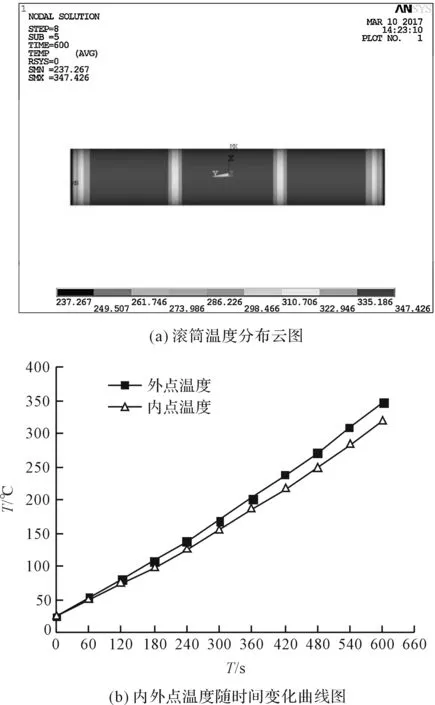
图6 滚筒电磁加热数值模拟结果

每段线圈加载有效电流密度为1.0×106A/m2，电流频率为15 kHz，加热时间为600 s，截取加热结束时滚筒温度云图，如图6(a)所示，从图可以看出滚筒表面温度比较均匀，只在两段线圈交界处和滚筒两端存在温度差，这是由于端部漏磁造成的。取滚筒中心位置外壁上一点(以下简称外点)和滚筒中心位置内壁上一点(以下简称内点)作为测温点，得到温度随时间的变化曲线。

3 模拟结果分析

在电磁加热中，滚筒的加热效果受很多因素的影响，其中，电流频率f、电流密度J和线圈与滚筒之间的距离d是3个比较重要的因素，同时也是电磁加热装置设计的关键参数，根据工程估值确定参数选择范围，利用数值模拟技术，得到各因素对加热效果的影响。

3.1 电流频率对滚筒加热的影响

取电流密度J为1.5×106A/m2，线圈与滚筒的距离d为20 mm，加热时间为300 s，频率f分别为5 kHz，10 kHz，15 kHz，20 kHz，25 kHz，30 kHz，进行数值模拟。滚筒内外点温度与电流频率的关系如图7所示。

图7 电流频率对滚筒温度的影响

从图7可以看出，滚筒内外壁温度随着电流频率的增大而升高，但频率到达一定值后，温升速度有所减慢，同时由于电流频率越大，滚筒的集肤效应越明显，导致滚筒内外壁温差越大，影响茶叶杀青质量，所以在满足温升要求的前提下，选择较低的频率。

3.2 电流密度对滚筒加热的影响

本研究取电流频率f为15 kHz，线圈与滚筒的距离d为20 mm，加热时间为300 s，电流密度J分别为1.0×106A/m2，1.25×106A/m2，1.5×106A/m2，1.75×106A/m2，2.0×106A/m2，进行数值模拟。滚筒内外点温度与电流密度的关系如图8所示。

图8 电流密度对滚筒温度的影响

从图8可以看出，电流对滚筒的温度影响很大，电流密度越大，滚筒温升越快，电流密度与温度的关系近似二次函数关系，这是因为频率不变的情况，随着电流密度增大，总电流也增大，加热功率增大。同时由于集肤效应的存在，滚筒内外壁温差也随着电流密度的增大而增大。

3.3 线圈与滚筒之间的距离对滚筒加热的影响

由于线圈与滚筒之间存在间距，不同距离，加热效果也不同。本研究取电流频率f为15 kHz，电流密度J为1.5×106A/m2，加热时间为300 s，线圈与滚筒的距离d分别为20 mm，30 mm，40 mm，50 mm，60 mm，进行数值模拟。滚筒内外点温度与距离的关系如图9所示。

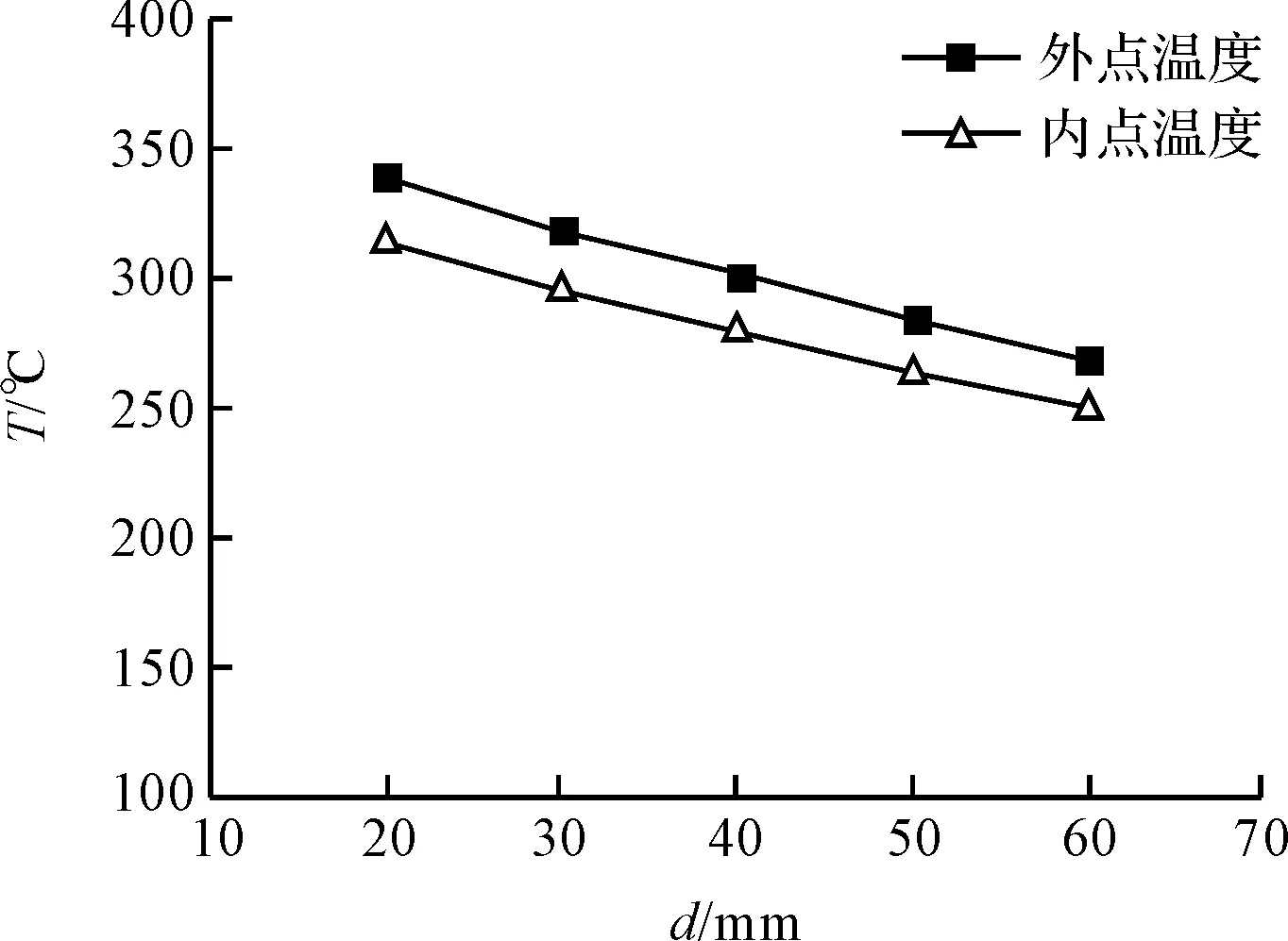
图9 线圈与滚筒之间的距离对滚筒温度的影响

从图9可以看出，线圈与滚筒之间的距离越小，滚筒温升速度越快，这是因为当线圈离滚筒表面越近时，穿过滚筒的磁力线越大，磁感应强度越大，滚筒加热效率越高，所以在保证安全的前提下，尽可能减小线圈与滚筒表面的距离，提高加热效率。

4 电磁杀青机电磁参数确定与试验

4.1 电磁杀青机关键参数设计

本研究设计的杀青机预热时间为5 min，温度设定值为300 ℃，以满足温升速度条件下，滚筒内外壁温差最小为设计目标，利用数值模拟结果进行正交试验[13]，试验因素及水平如表3所示。

表3 试验因素及水平

利用数理统计和正交性原理进行正交试验规划，以此进行滚筒电磁加热数值模拟，获得数据经统计得到的结果如表4所示。

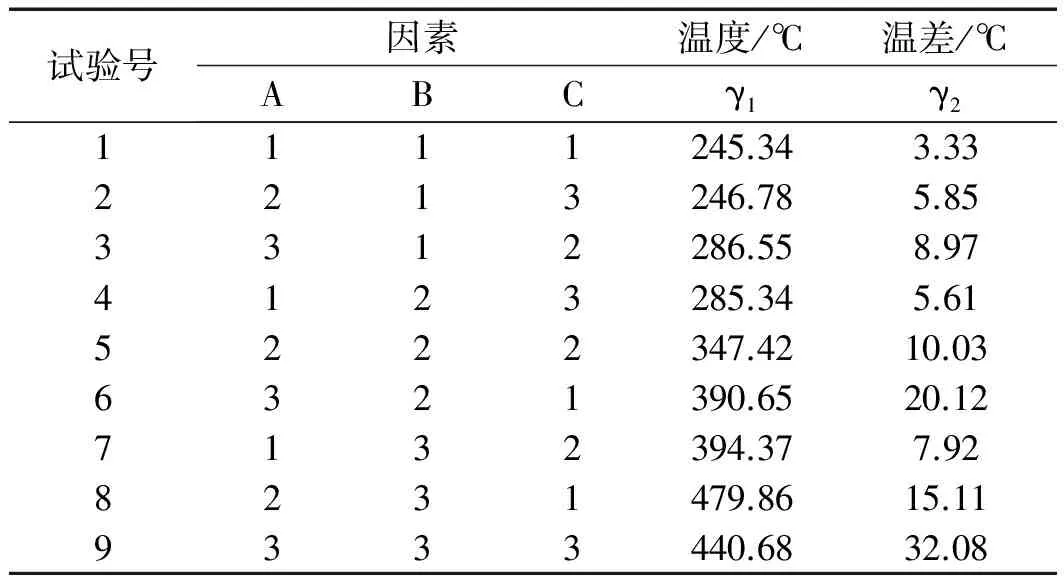
表4 正交试验结果

通过对正交试验结果分析，得到均值和极差，如表5和表6所示。

表5 温度正交试验分析结果

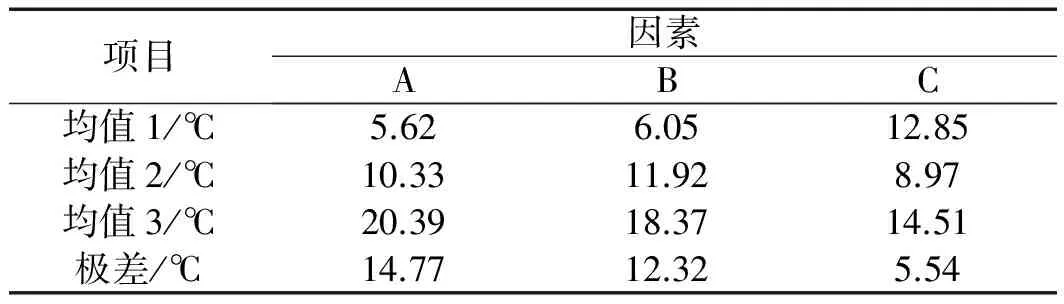
表6 温差正交试验分析结果

综合表5和表6可知，当电流频率为5 kHz，电流密度为1.75×106A/m2，线圈与滚筒的距离为30 mm时，滚筒温升速度达到设计要求且内外壁温差最小，将这组参数运用到电磁杀青机的设计中。

4.2 实验与结果分析

为了验证数值模拟分析结果的正确性，本研究与相同产能的电热式滚筒杀青机进行实验对比，选择茶鲜叶为福鼎大白茶，嫩度主要为1芽2叶，进行杀青试验，试验结果如表7所示。

两台杀青机的杀青效果对比如图10所示。

表7 杀青试验结果对比

图10 杀青效果对比

分析试验结果可得，设计的电磁杀青机基本符合要求，对比传统滚筒杀青机，预热时间缩短了13.7 min，预热速度提高约74%，单位质量杀青能耗减少0.24 kW·h，下降约38%，温度的控制精度达到±2 ℃，提高了7.5倍。对比杀青效果可以看出，电磁杀青机杀青叶失水均匀，而电热式滚筒杀青机容易出现茶叶杀不透的情况，杀青质量明显不如电磁杀青机。

5 结束语

用传统经验对电磁杀青机进行设计，存在较大的盲目性。本研究采用数值模拟技术，结合工程实践，开展了对电磁杀青机的研究。结果表明：利用数值模拟分析结果设计的电磁杀青机符合设计要求，可以减少实验次数，降低设计成本。

[1] 滑金杰,袁海波,尹军峰,等.绿茶电磁滚筒热风耦合杀青

工艺参数优化[J].农业工程学报,2015,31(12):260-267.

[2] 刘彦旭,刘保国.电磁加热技术在机械加工中的应用[J].现代制造技术与装备,2016(4):95-96.

[3] 赵宗彬,朱斌祥,杨大力,等.电磁加热节能技术在挤塑机加热系统中的应用研究[J].塑料工业,2014,42(2):72-74.

[4] JOHN W. The evolution of Maxwell’s equations from 1862 to the present day[J].IEEEAntennas&PropagationMagazine,2013,55(3):467-472.

[5] 陈天翔,王占军.电源频率对钢管感应加热过程影响的模拟试验及验证[J].金属热处理,2016,41(11):149-152.

[6] 易小开,李亮玉,岳建峰,等.输送管道中频感应加热的磁-热耦合仿真[J].金属热处理,2016,41(7):154-158.

[7] 杨毅青,龚继文.基于电磁感应原理的薄壁件铣削振动抑制[J].振动、测试与诊断,2015,35(3):429-433.

[8] 陈清伟,邱望标,陈伟兴.基于ANSYS的集肤效应分析[J].贵州科学,2012,30(1):58-62.

[9] 刘志儒.金属感应热处理(上册)[M].北京:机械工业出版社,1985.

[10] 常士家.注射机料筒电磁感应加热温度数学模型及数值模拟的研究[D].北京:北京化工大学机电工程学院,2010.

[11] 于恩林,韩 毅,范玉林,等.HFW管高频感应加热过程电磁热耦合数值模拟[J].焊接学报,2010,31(4):5-8.

[12] CHEN S C, PENG H S, CHANG J A. Simulations and verifications of induction heating on a mold plate[J].InternationalCommunicationsinHeatandMassTransfer,2004,31(7):971-980.

[13] 茆诗松,周纪芗,陈 颖.试验设计[M].北京:中国统计出版社,2012.