自动机凸轮机构的设计与动作协调性分析
2018-01-24顾寄南
陈 备,顾寄南
(江苏大学 机械工程学院,江苏 镇江 212000)
0 引 言
全自动胶囊生产线能够有效提高空心胶囊生产效率,大幅降低生产成本,提高利润率。其中自动机模块是生产线的核心模块,生产线的技术水平也主要体现在自动机模块,该模块负责完成空心胶囊生产流程中80%以上的动作。自动机模块又由更小的单元组成,其中主要包括夹囊单元、顶囊单元以及一些辅助单元,这些单元都由相应的凸轮驱动完成的,因此凸轮轮廓的精准设计直接关系到自动机及高速运行时的稳定性。除此之外,各个凸轮系统的协调动作对整个设备的运行至关重要,即通常所说的协调设计,在设计过程中,运动循环图能够帮助设计人员完成这一过程。运动循环图的主要能够完成以下工作[1-2]:
(1)确保执行构件的动作紧密配合、相互协调,使机器能够按照预期的的工艺过程顺利工作;
(2)为计算和提高机器生产效率提供依据;
(3)为具体设计各执行机构提供初始数据;
(4)为装配、调试机器提供依据。
然而,使用运动循环图辅助协调设计虽然简单明了,但在计算机实现辅助协调设计与优化的过程中存在一些不足[3]:
(1)协调设计所需的模糊性、层次性和继承性无法通过工作循环图体现;
(2)无法从宏观上指导设计,当工艺动作过程复杂时,工作循环图无法向设计者提供相关修改信息;
(3)在计算机辅助协调设计过程中缺少理想算法,无法通过计算机辅助完成协调设计。
本研究将选择统筹法对自动机进行协调设计[4-5],并根据自动机械协调设计的特点以及统筹法的特点和基本要求,建立自动机械协调设计的搭接网络模型。
1 自动胶囊生产线自动机的工作原理
自动机工作原理如图1所示。

图1 自动机工作原理1—前支架;2—夹套本体;3—顶杆;4—套合体;5—模条;6—夹钳;7—导向轴;8—V形块
在全自动胶囊生产线中,自动机的作用主要是将空心胶囊两个独立的部分即帽与体组合在一起,使其成为一个整体,如图1(a)所示。
其工作过程为:当套有胶囊帽的模条5送到指定位置时,传动轴7推动夹钳6向右运动,使夹钳6上方的钳口套住模条5上的胶囊帽;然后V形块8上升将夹钳6的下方向两侧挤开,使得上方合在一起,从而将胶囊帽夹住;传动轴7推动夹钳6向左运动,将胶囊送入夹套本体2内,夹套本体2向左运动,使夹套本体2最右侧与前支架1右侧对齐;然后前支架1、夹套本体2、顶杆3一起向上运动,使得夹套本体2的中心与套合体4的中心处于同一水平面,如图1(b)所示。然后夹套本体向右运动,与套合体4相接触,与此同时,推杆3也一同向右运动,当夹套本体2与套合体4接触之后,推杆3继续运动,进而将胶囊帽推入套合体4内,与套合体4另一侧送入的胶囊体组合成一个整体;然后前支架1、夹套本体2、顶杆3按原路返回,回到初始位置,进行下一个循环。
在整个运动过程中,其中夹套本体2与顶杆3起着至关重要的作用,且夹套本体2与顶杆3的驱动通过凸轮完成,并且在夹套本体2与顶杆3的运动过程中,为了避免顶杆3将夹套本体2内的胶囊帽顶出,则在夹套本体2运动到位之前,顶杆3的位移应小于夹套本体2的位移,这在下文凸轮的设计中会具体涉及到。
2 搭接网络模型
在搭接网络计划中,工作间的逻辑关系是由相邻两件工作之间的不同搭接关系确定的[6-7],故协调设计的多层网络模型的逻辑关系也是通过搭接关系实现的,在搭接网络技术中,搭接关系有4种基本形式,即FTS(完成到开始)型、STS(开始到开始)型FTF(完成到完成)型、STF(开始到完成)型[8-10]。
搭接关系形式如图2所示。
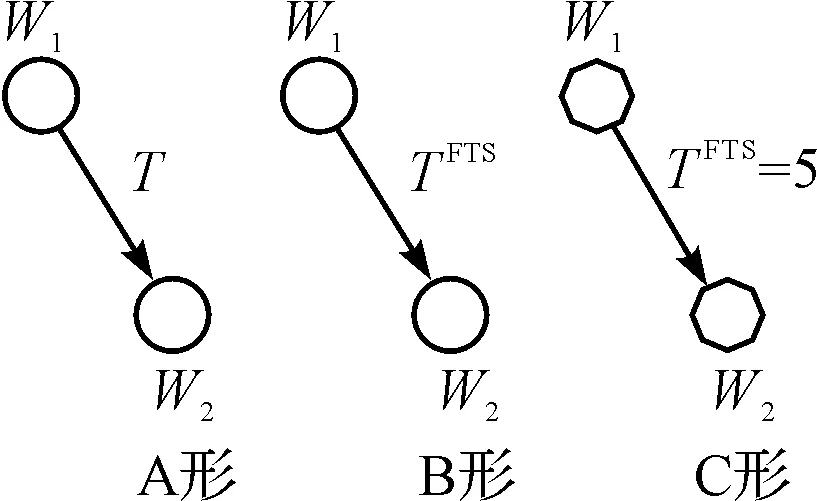
图2 搭接关系形式
C形搭接关系的表达形式中,T表示搭接关系,表示时距为5。为了适应协调设计的模糊性要求,增加了两种形式,若工作和确有搭接关系,但具体类型和时距不可知或难以确定,用A型;若工作和搭接关系类型已知,但时距难以确定,则用B型。
时间间隔及时间参数标注形式如图3所示。

图3 时间参数标注形式工作i的延续时间;工作i的最早开始时间工作i的最早完成时间;工作i的最迟开始时间;工作i的最迟完成时间
2.1 工艺流程与工艺动作层
由第一节分析得到自动机的工艺流程,即:(1)夹钳进给;(2)V形块上升;(3)夹钳6后退;(4)V形块下降;(5)夹套本体后退;(6)升降器上升;(7)夹套本体进给;(8)顶杆进给;(9)夹套本体后退;(10)顶杆后退;(11)升降器下降,即完成一个工作循环。
动作(1)夹钳6进给与动作(3)夹钳6后退通过剥囊凸轮驱动完成,分别用B11与B12代表动作(1)与动作(3);动作(2)V形块上升与动作(4)V形块下降通过V形器凸轮驱动完成,分别用B21与B22代表动作(2)与动作(4);动作(5)夹套本体后退、动作(7)夹套本体进给与动作(9)夹套本体后退通过夹囊凸轮驱动完成,分别用B31、B32与B33代表动作(5)、动作(7)与动作(9);动作(6)升降器上升与动作(11)升降器下降通过升降凸轮驱动完成,分别用B41与B42代表动作(6)与动作(11);动作(8)顶杆进给与动作(10)顶杆后退通过顶囊凸轮驱动完成,分别用B51与B52代表动作(8)与动作(10)。
工艺动作层如图4所示。

图4 动作层S、E—一个工作循环的开始和结束
2.2 添加时间关系
随着工艺流程的确定,以及执行机构的类型确定之后,此时各执行动作的组成区段可以确定,其时间可凭经验或实验得到估计值,搭接关系的时距也可给出估计值,也就是说网络模型的基本要素可以确定,其结果如图5所示。

图5 结构层
图5中B32夹套本体进给与B51顶杆进给在工作过程中,应保证在夹套本体运动到位之前,顶杆位移小于夹套本体,故此时动作B32夹套本体进给的延续时间暂时未知,将在第四节凸轮设计过程中确定。
3 协调性解决措施
由上述的分析可知,自动机的各个单元都是通过凸轮驱动的,为了解决自动机各个单元的协调性问题,最重要的是设计合理的凸轮机构。本文拟采用解析法设计凸轮机构[11-14],其基本思路:根据夹囊、顶囊运动要求及其结构尺寸,建立凸轮机构设计的数学模型,确定凸轮基圆半径,末端执行机构运动规律,凸轮行程等基本参数,再综合考虑凸轮的运动要求(是否失真)、压力角(小于许用值)、冲击等因素,得到满足要求的凸轮轮廓曲线。
3.1 顶囊单元
通过第三节的分析可知,顶囊单元驱动凸轮曲线选用单停留曲线,基圆半径r0=70 mm,滚子半径rr=28 mm。凸轮以等角速度沿顺时针方向回转,在凸轮转过角δ1=75°的过程中,推杆上升h=45 mm;凸轮继续转过δ2=75°的过程中,推杆下降h=45 mm,在推杆上升与下降过程中,凸轮轮廓曲线采用五次样条曲线;凸轮转过一周的其余角度时,推杆静止不动。
(1)推程阶段。凸轮推程运动角δ1=5 π/12,既当δ=0°~75°时,凸轮轮廓曲线采用五次样条曲线,s=h·[10(δ/δ1)3-15(δ/δ1)4+6(δ/δ1)5],上升到h=45 mm,则凸轮理论轮廓曲线的极坐标参数方程为:
(1)
θ=δ
(2)
(2)回程阶段。凸轮回程运动角δ2=5 π/12,既当δ=75°~150°时,凸轮轮廓曲线采用五次样条曲线,s=h-h{10[(δ-δ1)/δ2]3-15[(δ-δ1)/δ2]4+6[(δ-δ1)/δ2]2},下降到起始位置,则凸轮理论轮廓曲线的极坐标参数方程为:

(3)
θ=δ
(4)
(3)近休止段。凸轮近休止角δ3=7π/6,既当δ=150°~360°时,推杆在距凸轮回转中心最近位置保持不动,则凸轮理论轮廓曲线的极坐标参数方程为:
ρ=r0
(5)
θ=δ
(6)
3.2 夹囊单元
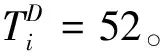
通过第二节的分析可知,夹囊单元基圆半径r0=80 mm,滚子半径rr=28 mm。凸轮以等角速度沿顺时针方向回转,在凸轮转过角δ1=52°的过程中,推杆上升h1=38 mm;凸轮继续转过δ2=23°,推杆静止不动,凸轮继续转过δ3=75°的过程中,推杆下降h2=35.5 mm,凸轮继续转过δ4=119°的过程中,推杆静止不动,凸轮继续转过δ5=21°的过程中,推杆下降h3=2.5 mm,回到初始位置。为了克服推杆在推程与回程过程中的震动问题,夹囊单元凸轮拟采用五次样条曲线。
(1)推程阶段。凸轮推程运动角δ1=13 π/45,既当δ=0°~52°时,凸轮轮廓曲线采用五次样条曲线,s=h1·[10(δ/δ1)3-15(δ/δ1)4+6(δ/δ1)5],上升到h1=38 mm,则凸轮理论轮廓曲线的极坐标参数方程为:
(7)
θ=δ
(8)
(2)远休阶段。凸轮远休止角δ2=23 π/180,既当δ=52°~75°时,推杆在距凸轮回转中心最远位置保持不动,s=h1=38 mm,则凸轮理论廓线的极坐标参数方程为:
ρ=118
(9)
θ=δ
(10)
(3)回程Ⅰ阶段。凸轮回程运动角δ3=5 π/12,既当δ=75°~150°时,凸轮轮廓曲线采用五次样条曲线,s=h1-h2{10[(δ-δ1)/δ2]3-15[(δ-δ1)/δ2]4+6[(δ-δ1)/δ2]5},下降h2=35.5 mm,则凸轮理论轮廓曲线的极坐标参数方程为:

(11)
θ=δ
(12)
(4)近休Ⅰ阶段。凸轮近休Ⅰ阶段休止角δ4=119 π/180,既当δ=150°~269°时,推杆在s=h1-h2=2.5 mm位置保持静止,则凸轮理论廓线的极坐标参数方程为:
ρ=82.5
(13)
θ=δ
(14)
(5)回程Ⅱ阶段。凸轮回程运动角δ5=7 π/60,既当δ=269°~290°时,凸轮轮廓曲线采用五次样条曲线,s=h3-h3{10[(δ-δ1-δ2-δ3-δ4)/δ5]3-15[(δ-δ1-δ2-δ3-δ4)/δ5]4+6[(δ-δ1-δ2-δ3-δ4)/δ5]5},下降到起始位置,则凸轮理论轮廓曲线的极坐标参数方程为:
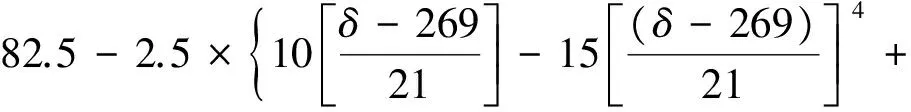
(15)
θ=δ
(16)
(6)近休止段。凸轮近休止角δ6=7 π/18,既当δ=290°~360°时,推杆在距凸轮回转中心最近位置保持不动,s=0,则凸轮理论轮廓曲线的极坐标参数方程为:
ρ=80
(17)
θ=δ
(18)
3.3 建模与分析
本研究借助Excel的数据计算功能对凸轮各坐标数据进行计算,得到各个点的坐标,利用CAD的样条曲线功能得到凸轮的理论轮廓曲线,如图6所示。

图6 凸轮轮廓曲线
顶囊凸轮与夹囊凸轮的了理论轮廓曲线如图6中1、3所示,因为滚子半径rr=28 mm,将理论轮廓曲线向内偏移14 mm;图6中2、4为实际轮廓曲线。
本研究通过creo对凸轮进行三维建模,得到凸轮的三维实体模型,并通过CREO对机构进行运动学分析,得到末端执行机构的加速度曲线,如图7所示。

图7 凸轮的加速度曲线
由曲线图可以看出,执行机构的加速度曲线连续,故自动机在运动过程中理论上不存在冲击,有效地避免了震动。
因为顶杆位于夹套本体内部,为了避免顶杆与夹套本体在运动过程中,顶杆将胶囊顶出,故在凸轮转角0°≤δ≤52°的过程中,顶杆位移应小于夹套本体位移,即Δs≤0。
令:

(19)
易求得在0°≤δ≤52°的过程中,f(δ)<0恒成立,故设计的凸轮满足使用要求。
4 结束语
本研究通过搭接网络模型直观地表达出自动机的
工艺动作过程及各动作持续时间,为通过计算机实现计算机辅助协调设计提供了一定的基础;通过凸轮轮廓线的设计实现自动机各单元的协调运行,能够满足自动机的使用要求。
下一阶段,本研究将基于自动机搭接网络模型,通过相应算法以实现对自动机时序关系进行优化。
[1] 詹启贤.自动机械设计[M].北京:轻工业出版社,1987.
[2] 汤 瑞.轻工自动机[M].上海:上海交通大学出版社,1985.
[3] 吕方梅,冯 涛.自动机械协调设计的搭接网络模型[J].机械设计,2002,19(1):4-7.
[4] 郭耀煌.运筹学与工程系统分析[M].北京:中国建设工业出版社,1986.
[5] JD惠斯特,FK莱维,著;葛震明,译.统筹方法管理指南[M].北京:机械工业出版社,1983.
[6] 朱弘毅.网络计划技术[M].上海:复旦大学出版社,1999.
[7] 汪 利.基于功能-行为-结构的机构系统设计智能化平台模型[J].机械设计与研究,1998,14(s1):6-7.
[8] 冯 涛,邹慧君,梁庆华,等.一种能设计计算机械工作循环的概念设计过程模型[J].上海交通大学学报,2002,36(3):367-372.
[9] 邹慧君.机械系统设计[M].上海:上海科学技术出版社,1996.
[10] 冯 涛,邹慧君,郭为忠,等.自动机械协调设计的多层网络模型[J].上海交通大学学报,2001,35(12):1825-1829.
[11] 郑文纬,吴克坚.机械原理[M].北京:高等教育出版社,2001.
[12] 程立斌,潘 嘹,徐 贞,等.钢提桶塑料提梁自动弯曲机构的设计[J].包装与食品机械,2016(2):70-72.
[13] 韩泽光,孙 哲,郝瑞琴,等.凸轮机构尺寸参数的优化设计[J].机械,2015(4):18-22.
[14] 刘昌淇.刘庆立.蔡昌蔚.自动机械凸轮机构实用设计手册[M].北京:科学出版社,2013.
