Delta机器人动力学建模与弹性误差分析*
2018-01-24陈君杰李攀磊许杨剑王效贵
陈君杰,李攀磊,韩 威,许杨剑,王效贵
(浙江工业大学 机械工程学院,浙江 杭州 310014)
0 引 言
1985年,瑞士的Clavel[1]发明了Delta并联机器人,该型机器人为三自由度空间平移机构,具有承载能力强、运动耦合弱、力控制容易等优点。随着并联机器人的应用领域不断得到拓展,其工作环境日趋复杂,并联机器人不断向高速度、高加速度、高精度、重载荷和轻量化方向发展[2-3],导致机构运行中弹性振动和运动误差也随之增加。传统的刚体动力学分析方法无法满足弹性误差分析的需求,考虑构件弹性的动力学分析成了研究重点。通过运动弹性动力学分析方法(kineto-elasto-dynamic,KED),将机构位移视作弹性位移与刚体位移(名义位移)的叠加,在给定机构名义运动条件规律的条件下,确定机构的弹性响应。
Piras[4]利用有限元理论与弹性动力分析方法(KED)研究了3-PRR平面并联机器人的弹性动力学问题。刘善增等人[5]建立了刚柔耦合并联机构系统的整体动力学方程的步骤与方法,对3-RRS并联机器人的频率特性进行了分析。韩亚峰等人[6]利用有限元理论,采用平面梁单元对Delta机器人进行了弹性动力学建模。Kuo等人[7]基于D-H方法定义了一组全局变量,在不使用约束方程的情况下,导出了Delta机器人的弹性动力学模型。目前,Delta并联机器人的弹性动力学研究中大都认为其四边形从动臂机构在运动过程中两侧杆保持平行,从而将其四边形从动臂机构简化为一根虚拟从动杆进行分析,而在实际运动过程中,由于驱动杆末端弹性转角等影响,四边形机构会产生扭曲,有必要针对机器人的四边形机构进行动力学建模研究。
本研究将Delta机器人四边形从动臂机构划分为2刚性短杆与2柔性从动杆,通过分析其运动协调条件,在有限元理论基础上建立Delta机器人的弹性动力学方程,通过数值方法求解出机器人在运动轨迹中的弹性误差,并通过改变杆件截面尺寸,分析杆件截面尺寸对弹性误差的影响。
1 弹性动力学方程
Delta并联机器人结构图如图1所示。
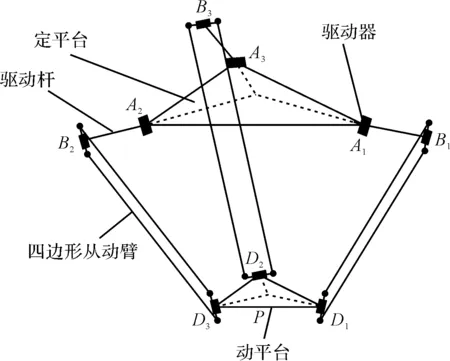
图1 Delta并联机器人结构图
Delta机器人由定平台、驱动器、驱动杆、四边形从动臂、动平台等组成,其中连接动平台与定平台的3个支链互成120°角对称分布。每条支链包含一个驱动杆与一个从动臂,驱动杆一端通过驱动电机与定平台相联接,另一端以转动副形式与从动臂相连,从动臂为平行四边形结构,确保动平台在工作空间内做三维平动。因为构件的柔性以及运动过程中惯性力和外载荷的影响,动平台中心点P的实际位置相对于理想位置产生偏差,即弹性位置误差,通过建立Delta机器人的弹性动力学方程可以对其弹性位置误差进行计算。
1.1 单元划分及位移分析
根据有限元理论,笔者选择矩形截面梁单元作为基本单元,用以划分机构中的柔性杆件,空间梁单元模型如图2所示。

图2 空间梁单元模型
单元包含2个节点。每个节点有6个弹性位移自由度,表示梁单元弹性位移的广义坐标:
(1)
式中:x1,x2—两节点在x轴向的弹性位移;y1,y2—两节点沿y向弹性位移;z1,z2—两节点沿z向弹性位移;φx1,φx2—两节点绕x轴弹性转角;φy1,φy2—两节点绕y轴弹性转角;φz1,φz2—两节点绕z轴弹性转角。
根据欧拉-伯努利梁理论,梁单元上任意一点弹性位移可以表示成如下形式:

(2)

(3)

(4)

(5)

1.2 单元弹性动力学方程
因为单元弹性变形较小,忽略机构刚体运动与弹性变形运动之间的耦合影响,单元的位移看作是刚体位移与弹性位移的叠加,单元动能为:
(6)


(7)
式中:ρ—单元质量密度;L—梁单元长度;A—梁单元截面面积;IP—梁单元横截面对x轴的极惯性矩。
单元的变形能包括弯矩、轴向力和扭矩作用时所产生的能量,单元总变形能为:
(8)
式中:Ke—单元刚度矩阵。

(9)
式中:E—梁单元材料的杨氏模量;G—梁单元材料的剪切模量;Iy,Iz—梁单元横截面对y轴和z轴的极惯性矩,形函数下标中的x以及xx分别代表对x的一阶偏导和二阶偏导,例如:Nux代表Nu对x的一阶偏导。
将式(6,8)代入拉格朗日动力学方程,导出单元弹性动力学方程:
(10)
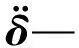
Fe=Qe+Pe+Ge
(11)
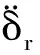
1.3 运动协调关系
1.3.1 支链内坐标系建立
鉴于Delta机器人支链的对称性,本研究选取一条支链进行弹性动力学建模。支链有限元模型如图3所示。
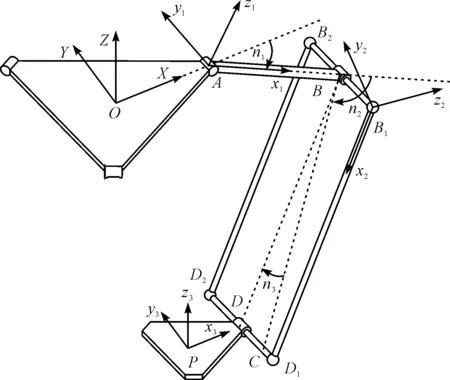
图3 支链有限元模型
图3中,A为驱动端,驱动杆AB被视为空间悬臂梁,B1B2D2D1为支链的平行四边形从动臂结构,P为机器人末端,因为平台刚度远大于空间梁单元机构,视动平台与定平台为刚性体。而在四边形机构中,上下短杆长度远小于两侧杆,因此本研究将B1B2、D1D2两杆视作刚性体,并忽略其质量影响,将B1D1、B2D2两杆作为弹性杆件进行分析。
本研究在图3中做驱动杆AB直线在B1B2D2D1平面上的投影BC,并如图中定义角度n1、n2、n3。建立支链O-XYZ坐标系,方向定义为Z轴向上,Y轴平行于驱动器转动轴线,X轴遵守右手定则指向支链方向;动平台坐标系P-x3y3z3方向与支链坐标系O-XYZ一致;驱动杆AB单元坐标系A-x1y1z1的坐标轴方向由支链坐标系O-XYZ绕Y轴旋转n1得到;从动杆B1D1单元坐标系B1-x2y2z2方向由支链坐标系O-XYZ先绕Y轴旋转n1+n2,后绕Z轴旋转n3得到。
定义支链弹性位移广义坐标为:
(12)
其中,前6项元素组成P点在坐标系P-x3y3z3下广义坐标UP,描述动平台因为机构弹性变形影响,P点相对于名义位置的位移;7~12项元素组成广义坐标UB,对应AB梁单元坐标系A-x1y1z1下B节点处的弹性位移;φ1-8分别为B1D1、B2D2两杆端点在各自单元坐标系下绕y轴与z轴方向的弹性转角。
1.3.2 支链内运动协调关系
驱动杆AB为空间悬臂梁,点A处的弹性位移与转角均为零,可以得出AB梁单元与支链弹性位移之间的关系为:
δAB=SABΨ
(13)
其中:
(14)
式中:I—单位矩阵;0—零矩阵;δAB—AB梁单元广义坐标。
记D点在动平台坐标系P-x3y3z3下广义坐标为:
(15)
则D点与P点位移协调关系为[8]:
(16)
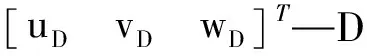
根据图3中几何约束关系可以得到B1D1梁单元在单元坐标系下的弹性位移:
x1=(xBc2+zBs2-d(φzBc2-φxBs2))c3+yBs3;
y1=-(xBc2+zBs2-d(φzBc2-φxBs2))s3+yBc3;
z1=zBc2-xBs2+d(φxBc2+φzBs2);
φx1=0;φy1=φ1;φz1=φ2;
x2=(xDc12+zPs12-d(φzDc12-φxDs12))c3+yDs3;
y2=-(xDc12+zDs12-d(φzDc12-φxDs12))s3+yDc3;
z2=zDc12-xDs12+d(φxDc12+φzDs12);
φx2=0;φy2=φ3;φz2=φ4
(17)
式中:d=1/2|B1B2|;符号s,c—函数sin和cos,下标数字对应3个角度n1、n2、n3,例如:s12代表sin(n1+n2),c3代表cosn3。
由式(16,17)可以得出B1D1梁单元与支链弹性位移之间的协调关系:
δBD1=SBD1Ψ
(18)
式中:δBD1—B1D1梁单元广义坐标;SBD1—B1D1梁坐标协调矩阵,同理可以得出B2D2梁单元与支链弹性位移之间的协调关系:
δBD2=SBD2Ψ
(19)
动平台P与支链弹性位移协调关系为:
UP=SPΨ
(20)
式中:
1.3.3 系统运动协调关系
本研究建立系统广义坐标U∈R48×1,根据式(13,18,19,20),以及3条支链的对称性,建立出任意构件i与系统广义坐标U之间的协调关系:
δi=SiU
(21)
式中:i—构件编号;δi—构件i的单元广义坐标;Si—对应的坐标协调矩阵。
1.4 系统弹性动力学方程
动平台为刚体,其动力学方程[9-10]可以表示为:
(22)
其中,动平台质量矩阵:
(23)

将式(19)代入式(10,22)得到各构件动力学方程:
(24)

将各构件的单元动力学方程(24)进行总装得到:

(25)

2 弹性误差分析
2.1 弹性误差计算
笔者选用系统参数:驱动杆长500 mm,动平台质量0.2 kg,上平台外接圆半径100 mm,动平台外接圆半径为50 mm,从动臂结构中短杆长度为50 mm,两侧的从动杆长600 mm,驱动杆截面与从动杆截面均选用正方形截面,驱动杆截面边长尺寸20 mm,从动杆截面边长尺寸10 mm,材料密度为7 850 kg/m3,弹性模量210 GPa,泊松比0.3,运行时间T=3s。给定动平台运动轨迹:
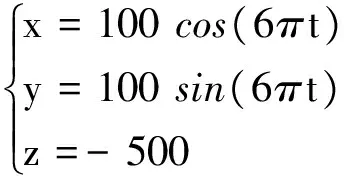
(26)
本研究利用Newmark方法在Matlab中对系统动力学方程(25)进行数值求解,计算出动平台末端P点的弹性位置误差在运行时间内的变化情况。
圆周轨迹下弹性位置误差如图4所示。

图4 圆周轨迹下弹性位置误差Δx、Δy、Δz—P点沿x、y、z三轴方向的弹性误差。
2.2 杆截面尺寸对弹性误差影响
通过改变驱动杆与从动杆的截面参数,可以有效改变机器人的力学性能。定义轨迹上误差均值:
(27)
式中:Δx(t),Δy(t),Δz(t)—P点在t时刻沿各轴向的弹性误差值。
2.2.1 驱动杆截面尺寸对弹性误差影响
驱动杆截面边长选择取值20 mm~30 mm的范围,其他参数不变。本研究根据式(27)计算误差均值随驱动杆的截面边长的变化情况。结果如图5所示。

图5 驱动杆截面尺寸对机构末端弹性误差的影响
可以看到:随着驱动杆截面边长增大,机器人末端的误差均值明显减少。究其原因,驱动杆的受力形式类似于悬臂梁,增加其截面尺寸能够有效提升其弯曲刚度。
2.2.2 从动杆截面尺寸对弹性误差影响
考察从动杆截面尺寸对机构弹性误差的影响,从动杆截面边长选择取值5 mm~10 mm的范围,其他参数不变。误差均值随从动杆截面边长的变化情况如图6所示。

图6 从动杆截面尺寸对机构末端弹性误差的影响
由图可以看到:当从动杆截面边长增大时,机构的均值误差随之增加。分析原因,从动杆两端均为球铰关节,其变形方式以拉压为主,相对于弯曲变形,轴向拉压变形的尺寸相对较小,其刚度的提升并不能抵消掉由质量增加带来的额外载荷影响。
2.2.3 两杆截面尺寸对弹性误差综合影响
笔者考察两种杆截面尺寸对机构弹性误差的综合影响,从动杆截面边长选择取值5 mm~10 mm的范围,驱动杆截面边长选择取值20 mm~30 mm的范围,其他参数不变,机器人均值误差随两杆截面尺寸变化如图7所示。

图7 两类杆截面尺寸对机构末端弹性误差的综合影响
可以看到在区间内均值误差的变化规律,误差均值与驱动杆截面尺寸呈负相关,与从动杆截面尺寸呈正相关,具有一定的单调性。
3 结束语
本研究针对Delta机器人运动过程中的弹性变形误差进行了分析,建立了系统的弹性动力学控制方程,通过数值方法进行算例分析,求解出了机器人在运动过程中的误差情况,分析了杆件截面尺寸对弹性误差的影响。
结论显示:通过增加驱动杆的截面尺寸以及减少从动臂的截面尺寸,能够有效降低机器人运动过程中的弹性变形。
[1] CLAVEL R, A fast robot with parallel geometry[C]. Proc.Int.symposium. on Industrial Robots, Lausanne: CiNii,1988.
[2] 计时鸣,黄希欢.工业机器人技术的发展与应用综述[J].机电工程,2015,32(1):1-13.
[3] 冯李航,张为公,龚宗洋,等.Delta系列并联机器人研究进展与现状[J].机器人,2014(3):375-384.
[4] PIRAS G, CLEGHORN W L, MILLS J K. Dynamic finite-element analysis of a planar high-speed, high-precision parallel manipulator with flexible links[J].Mechanism&MachineTheory,2005,40(7):849-862.
[5] 刘善增,朱真才,余跃庆,等.空间刚柔耦合并联机构系统的频率特性分析[J].机械工程学报,2011,47(23):39-48.
[6] 韩亚锋,马履中,吴伟光,等.Delta并联机器人弹性动力学研究[J].农业机械学报,2011,42(10):197-202.
[7] KUO Y L. Mathematical modeling and analysis of the Delta robot with flexible links[J].Computers&MathematicswithApplications,2016,71(10):1973-1989.
[8] 黄 真,孔令富,方跃法.并联机器人机构学理论及控制[M].北京:机械工业出版社,1997.
[9] 韩敬虎,俞经虎.食品检测咀嚼机器人工作空间研究[J].轻工机械,2016,34(3):1-4.
[10] 熊艳梅,杨延栋.码垛机器人运动学分析与仿真[J].机械,2015(12):62-66.
[11] 巴 特.有限元分析中的数值方法[M].北京:科学出版社,1985.
