音阶与数学

吴朝阳

留学美国时我曾有一位专攻巴松管的室友，他姓潘而又帅气，所以我称他为潘安。有一回我翻看潘安的乐谱时他问道：“你看得懂吗？”我笑着回答说：“不就是从0到7吗，我是学数学的，连8和9我都明白着呢！”

这个回答当然是玩笑，巴松乐谱都是五线谱，而使用0到7的是简谱。然而，音乐与数学确实存在着很深刻的联系。

旋律是由乐音的组合构成的，乐音按其频率从低到高排列，无论是想象中还是听觉上都像是一部阶梯，所以称为音阶。音阶系统中各乐音频率之间存在着特定的比例关系。这种数学关系自古以来就被确认和研究，并且被不断地完善。

2000多年前，古希腊和中国的学者就发现，当音阶间的频率关系是简单的比例时，它们构成的乐音系统是和谐的、悦耳的，并因此各自独立得出了构建音阶系统的方法。其中，中国上古的方法称为“三分损益法”，而在古希腊占据主流的则是“五度相生律”。这两种方法本质上是相同的，都是以2：1和3：2这2个最简单的比例为基础构建音阶系统。

在介绍音阶系统的构造之前，我们先简单说一说它背后的物理原理。首先，如果2个乐音的频率比例是2：1，那么后者的最小周期是前者的2倍，因而它的周期也都是前者的周期。这样一来，它听起来就像是前一个乐音，只不过前者听起来感觉声音更髙亢。因此，它们是同名乐音，我们说前者比后者“高八度”。假如频率较低的乐音是中央C（即简谱中C调的1），那么频率较髙的那个就是cl（即简谱中C调的i）。其次，如果2个乐音的频率比例是诸如3：2这样的简单比例，那么它们的周期间的关系

简单，叠加时形成的波也有简单的规律性（周期性），因此2个音的关系听起来是和谐的。例如，频率关系为3：2的2个正弦波的叠加具有如下简洁的周期性波形。

3：2这个除2：1之外最简单的比例听起来很和谐，在音阶系统中的地位也非常关键，具有这一比例乐音间的关系被称为“纯五度”。简言之，以2：1和3：2这2个比例为构造音阶的基础比例，是符合物理原理的。

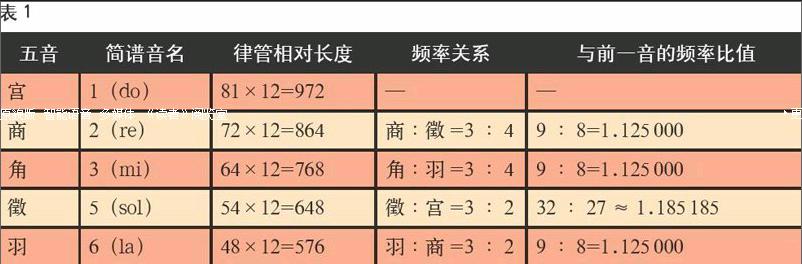
中国古代很早就出现了用三分损益法确定乐音频率的办法。《管子·地员》说：“凡将起五音凡首，先主一而三之，四开以合九九，以是生黄钟小素之首，以成宫。三分而益之以一，为百有八，为徵。不无有三分而去其乘，适足，以是生商。有三分，而复于其所，以是成羽。有三分，去其乘，适足，以是成角。”《史记·律书》则说：“九九八十一以为宫。三分去一，五十四以为徵。三分益一，七十二以为商。三分去一，四十八以为羽。三分益一，六十四以为角。”这2段文字所说的，都是用三分损益法确定宫、商、角、徵、羽五音的办法，其中的数字是用来确定音高的“律管”的（相对）长度。由于同质律管的发声频率与其长度成反比，因而这些数字就给出了宫、商、角、徵、羽的频率比例关系。2段引文不同的是，由于《管子》的做法是先益后损，因而其徵、羽的管长与《史记》所得为2倍关系，即其音高实际为低八度的徵、羽。我们根据《史记》所载，并且为了与后文的表格相比较，将宫的律管长度改记为81的12倍，则其五音可列表如表1。

从上面所引的文字可知，所谓“三分去一”是将原来的律管长度减去1/3，即所得管长为原来的2/3。因此所得乐音频率为原乐音的3/2倍，即2个乐音的频率比等于3：2。而所谓“三分益一”，所得的管长为原来的4/3倍，因此2个乐音的频率比为3：4。而若将第2个乐音用其高八度乐音替换，则频率比也是3：2。因此，三分损益法所确定的五音阶系统，是最简单的和谐系统，因而是最简单的音阶系统。自古以来，中国的五音阶音乐非常发达，显然正是由于这个原因。

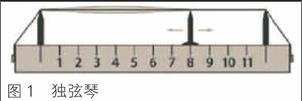
古希腊的毕达哥拉斯学派用类似于图1的独弦琴确定音阶，他们把全弦振动的音作为基础音。毕达哥拉斯学派同样发现，当整弦长度与振动部分弦长的比值可以表示成小整数的比例时，得到的就会是悦耳的音程。当振动部分弦长只有全弦长度的一半时，也就是图1中的琴码移动到“6”的位置时，弹拨琴弦得到的是比基础音高八度的乐音。也就是说，弦长比例为2：1时，弹拨独弦琴所发出声音之频率是全弦音频率的2倍。如果将琴码移动到图1中“8”的位置，全弦与所得弦长的比例是3：2，这时得到的是比基础音高五度的乐音。而如果将琴码移到“9”的位置，也就是全弦长度与振动部分弦长之比等于4：3时，得到的乐音则比基础音髙四度。整个毕达哥拉斯的音阶系统，就是在这种简单的弦长比例的基础之上建立起来的。

如果将独弦琴的全弦音定为D，将其弦长记为864个长度单位，那么比它高五度的音为A，其弦长为864x?=576。比A高五度的音为e，弦长为576x?=384，因此向一音域里的、比e低八度的E的弦长为384x2=768。而比D低五度的音的弦长等于864÷?=1296，其同一音域的音比这个音高八度，即比D高四度的G，其弦长则等于1296÷2=648。依此类推，可以得到全部7个音阶（见表2）。

对比以上2个表格可以发现，古代中外的两套系统中，do、re、mi、sol、la的音高关系是完全相同的。所不同的是，按照“原汁原味”的三分损益法继续产生音阶的话，我们得到的并不恰好是ti和fa，而是ti和“升fa”。这一不同表明，原始三分损益法所代表的古代中国音乐主要是五音阶的，虽然七音阶系统也不难由此产生。事实上，七音阶系统的音乐在古代中国也并不罕见，只不过另外2个乐音没有独立的名称，其中相应于ti的乐音称为“变宫”，fa称为“清角”，而“升fa”则称为“变徵”。换句话说，“宫、商、角、清角、徵、羽、变宫”构成一个“清乐”的七音阶体系，而“宫、商、角、变徵、徵、羽、变宫”则构成一个“雅乐”的七音阶体系。《史记》记载，荆轲在易水上“为变徵之声”，是中国古代七音阶音乐的一个著名例子。

由五度相生律产生的七音阶系统中，半音阶的频率比为256：243，這不是小整数的比例，因此听起来难免有不和谐之感，古代西方的“纯律”很可能就因为这个原因而产生。在纯律的体系里，“全音阶”分为“大全音”与“小全音”两种，其频率比分别为9：8和10：9。相应地，“半音阶”的频率比值不再是256：243这样的大整数之比，而是简单得多的16：15。这2种音阶体系中有些乐音的音商是不一样的，具体情形如表3。

由上述音阶系统中乐音间的频率比可以看到，音乐与数学存在着很深刻的联系，然而，音乐背后的数学还不止这些，因为我们至此仅仅讨论了简单的音阶体系，还没有涉及复杂的音乐。事实上，复杂的音乐一般采用多个不同的调式或含有多个声部。通俗地说，这些复杂音乐是以不同音高作do的多个旋律片段的组合。因此，不同调式或声部的乐音之间的“和谐”就必然是一个问题。而无论是纯律还是五度相生律，在多调式或多声部的情况下通常都是“不和谐”的。这个问题至少2000年前就已经被发现，而它最终导致十二平均律的出现。那么，十二平均律背后有什么样的数学奥秘？这个问题以后我们有时间再谈。endprint