Research on SFLA-Based Bidirectional Coordinated Control Strategy for EV Battery Swapping Station

Guo Zhao, Jiang Guo and Hao Qiang

1 Introduction

In recent decades, the issues of energy shortage and environment pollution have increasingly become worldwide concerns. As a new green traffic tool, EVs have been demonstrated considerable advantages in solving the energy crisis and reducing the emissions of carbon dioxide, as well as in providing a means to drastically reduce the man-made pollution [Williams, DeBenedictis and Ghanadan et al. (2012); Aziz, Oda and Mitani et al. (2015); Du, Wang and Lv (2016)]. As the large-scale EVs participate in power grid operation, the power load would rise significantly. The charging behavior of EVs is of randomness and intermittence, and the impact of large-scale EVs on the grid would gradually appear as follows: the EVs charging time may be concentrated, thus resulting in local load peak and drastic fluctuations in the load of power grid. Therefore,coordinated charging is urgent to effectively smooth the load profile. Furthermore, it could potentially provide flexible services to the grid, e.g. load shifting, balancing power,and frequency response [Zhang, Zhang and Xiong et al. (2014); Yang, Zhang and Niu et al.(2015); Zhao, Huang and Qiang (2015); Xia, Lai and Zhong et al. (2016); Vahedipour-Dahraie,Rashidizaheh-Kermani and Najafi (2017)].

Enabling bidirectional power flow, V2G services offer a wide range of benefits and revenues. And in fact, the coordinated strategies proposed in most researches are applied to control over the charging/discharging behavior of huge EVs batteries. Aggregated many batteries, battery swapping stations could be regarded as energy storage power stations, which effectively could carry out the coordinated strategies to achieve the benefits and revenues offered by V2G. Rao R. et al. proposed an optimization charging mode (OCM) and simulated the impacts of OCM on the power grid side and generation side [Tan, Ramachandaramurthy and Yong. (2016)]. Xie P. et al. applied Monte-Carlo stochastic simulation method to estimate the equivalent controllable capacity of battery swapping stations, presented the lumped S2G equivalent model subject to SOC limits and CC constrains, and proposed a filter-based AGC coordinated strategy [Xie, Li and Zhu et al. (2016)]. Zhang Q.D. et al. used genetic algorithm to solve the scheduling model which took the economic operation of battery swapping stations and the optimal switching frequency of charging/discharging machine as the goals [Zhang, Huang and Chen et al. (2015)]. Yang J. et al. proposed a modified genetic algorithm to study the electric vehicles battery swap station location and inventory problem which was formulated as an integer program [Yang and Sun (2015)]. Sun L. et al. analyzed the start-up characteristics of a generator powered by batteries and proposed a bi-level optimisation-based network reconfiguration model to determine the restoration paths with an objective of maximizing the overall generation capability, and solved this problem by the well-established particle swarm algorithm [Sun, Wang and Liu et al.(2015)]. Kang Q. et al. presented a novel centralized charging strategy of EVs under the battery swapping scenario by considering optimal charging priority and charging location (station or bus node in a power system) based on spot electric price, and introduces a dynamic crossover and adaptive mutation strategy into a hybrid algorithm of particle swarm optimization and genetic algorithm to implement the charging strategy[Kang, Wang and Zhou et al. (2015)].

With the popularization of EVs, battery swapping stations will increase rapidly and arouse more and more attentions. In this paper, we mainly investigated the bidirectional power flow between the station and power grid and designed a SFLA-based control strategy to smooth the load profile. Compared to particle swarm optimization (PSO)method, the presented SFLA-based strategy can effectively lower the peak-valley difference with the faster convergence rate and higher convergence precision.

2 Optimization model of EV battery swapping station

According to the “technical guide for electric vehicle battery-swap station” presented by the State Grid Corporation of China (SGCC), one charger for EV is used to charge one battery box. In the battery box, there is a battery pack, which consists of a plurality of battery cells. The battery mentioned in this paper refers to the battery pack. There are two types of battery in EV battery swapping stations, which are called regulated batteries,connected to EV battery chargers and participating in the grid coordinated control, and full-charged reserve batteries, disconnected to chargers and only used when not meeting the demand for swapping battery. Only regulated batteries are considered in this paper.

In order to investigate the bidirectional coordinated control strategy for EV battery swapping stations, some assumptions are made as follows.

1) Under normal circumstances, there are sufficient chargers, and batteries in the state can meet the user's needs.

2) Irrespective of the diversity of batteries [Chen, Li and Hong (2015)], all batteries are considered of the same type, and with the same initial charging state (SOCb) of 20% and the same end-charging SOC of 100%.

3) In optimization model, meeting the energy exchange purpose is a priority. And the constraint of battery continuous charging would be ignored. Furthermore, we assume that the charging or discharging power would be achieved within an allowable range.

4) At the beginning of optimization period, set as 0:00, the regulated batteries with full charge are only swapped out for the user’s demand, and don’t perform the charge and discharge operations.

2.1 Optimization objective function

In energy exchange model, EV battery-swap stations can play its positive role in smoothing the load fluctuation and improving the grid operation. Then, the minimum variance of the load profile including the charging load generated by EV battery-swap stations in one area is treated as the optimization objective.

In view of assumption (3), batteries would not be charged by the typical two-stage method mentioned in [Qiang (2015)]. Therefore, one optimization periodTOcould be arbitrarily divided into multi-sections (Mb), and each section has the same durationTb.

Obviously, a largerMbimplies the higher precision of the model with the greater amount of computation, and vice versa.

Then, the optimization objective can be expressed as [Huang, Qiang and Zhang et al.(2013)]

where Pd,jrepresents the predicted daily load power of thejthsection excluding the charging load generated by EV swap station;Nis the total number of EV battery chargers; Pi,jstands for the charging or discharging power of theithbattery in thejthsection. A positive Pi,jindicates that the battery is charging, and a negative Pi,jindicates that the battery in a discharged state. If Pi,jequals to zero, it indicates that the battery is in the off-working state.

2.2 Constraints

In addition to meeting the user demand for battery replacement, EV battery swapping station plays an active role as energy storage unit in the grid operation. Then, the charging or discharging power and battery capacity must be considered.

2.2.1 Power constraint

The overlarge power may cause damage to the charge- discharge device, which is used to exchange energy between the batteries and grid. Therefore,

wherePdevice_dmaxandPdevice_cmaxrespectively represent the maximum charging and discharging power of devices；Pbattery_dmaxandPbattery_cmaxstand for those of batteries.

2.2.2 Battery capacity constraint

According to the battery specification, there are upper and lower limits to battery capacity. Namely, the battery would be charged up to the upper limit and stopped discharging when its capacity drops down to the lower limit. Based on the assumption(2), all the batteries have the identical capacity and it can be expressed as

whereQmaxandQminare the upper and lower limits of battery capacity when charging or discharging. Considering the relationship between SOC and capacity of batteries, it is easy to deduce that at any time the SOC should meet

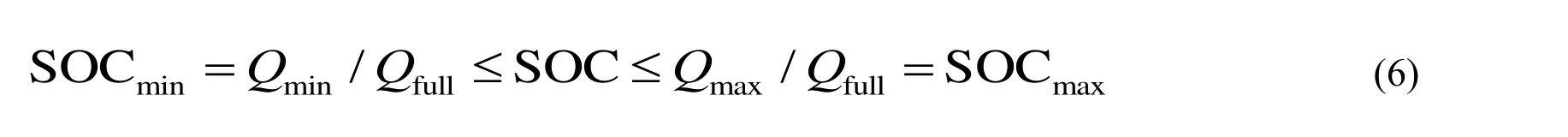
whereQfullstands for the battery capacity in the full charge state.

For the batteryi,tin(i) denotes its swap-in section. And according to the assumption, the charging or discharging operation of the battery would be performed from the next sectiontin(i) + 1. Then at the beginning of sectionj, its capacityQi,jcan be expressed as the accumulation of the initial capacity deduced with the SOCband the change of capacity from the sectiontin(i) + 1 tojdue to charging or discharging,

Substitute Eq. (7) into Eq. (6) and yield

In order to reduce the variables of the model, the further assumption is made

Substitute Eq. (7) and Eq. (9) into Eq. (8), then yield

2.2.3 User demand constraint

As the main means of energy supply to EVs, the primary function of swap station is to provide sufficient full-charged batteries to satisfy the user’s demands. Therefore, it is obvious that the charging or discharging operation of the battery would be done during the sectiontin(i) + 1 to the sectiontout(i) - 1, wheretout(i) denotes the swap-out section of theithbattery. Then the sectionjwould be an integer and meet

Batteries must be full-charged when they are swapped out. So,

Evidently,Pi,tout(i)-1is non-negative. So the battery would not be discharged in the sectiontout(i) - 1.

Substitute Eq.(7) into Eq. (12) and yield the charging power in the sectiontout(i)–1 .

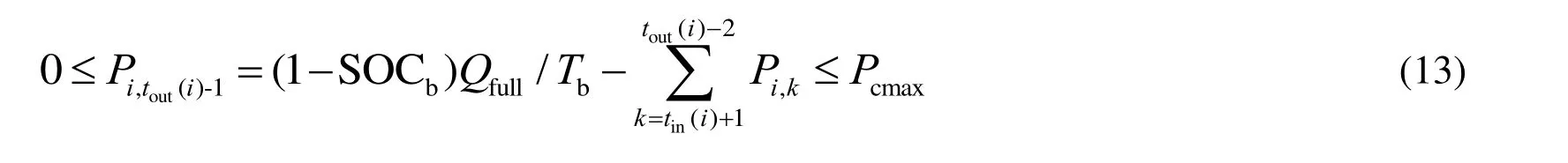
Through the above analysis, it is important to note that the full-charged regulated batteries could be charged only after discharged, while the batteries swapped into station would be discharged just after charged.

3 SFLA-based energy exchange optimal control strategy

3.1 Shuffled frog leaping algorithm

SFLA is a bio-inspired optimization technique and imitates and models the behavior of frogs searching for food laid on discrete stones randomly located in a pond [Huang, Qiang and Zhang et al. (2013); Eusuff and Lansey (2003); Ebrahimi, Hosseinian and Gharehpetian (2011)]. In SFLA there is a population, which consists of a set of frogs(solutions). The set of frogs is partitioned into subsets referred to as memeplexes.

Different memeplexes are considered as different cultures of frogs, and each memeplex performs a local search. Within each memeplex, the individual frogs hold ideas, which can be influenced by those of other frogs, and evolve through a process of memetic evolution.Frog leaping improves an individual’s meme and enhances its performance towards the goal. After a predefined number of memetic evolution steps, ideas are passed among memeplexes in a shuffling process. The local search and the shuffling processes continue until the defined convergence criteria are satisfied.

SFLA involves a population of possible solutions defined by a set ofprandomly generated frogs denoted asis the position of theith frog in thedimensions search space. All the frogs are sorted in a descending order according to their fitness, and the population is divided intommemeplexes, each containingnfrogs (i.e.,p=m×n), in such a way that the first frog goes to the first memeplex, the second frog goes to the second memeplex, themth frog goes to themth memeplex, and the (m+ 1)thfrog goes back to the first memeplex, and the process continues in this manner.

In each memeplex the frogs with the best and the worst fitness are represented byXbandXw, respectively. The best frog in the whole population is denoted byXg. During memeplex evolution, the worst frogXwleaps toward the best frogXb, which is formulated as the following updating rule

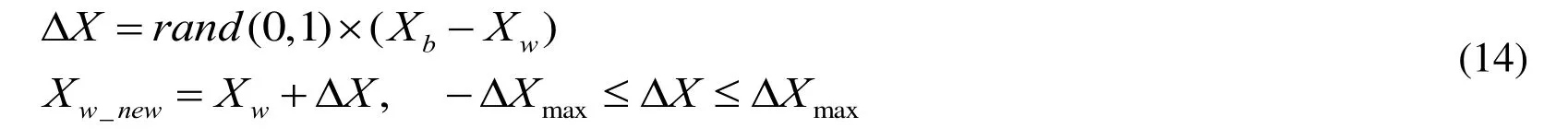
where, ΔXdenotes the updated step size for frog leaping; rand (0,1) generates a random number between (0, 1); and ΔXmaxis the maximum distance in one leaping. If Xw_newhas better fitness, the worst frogXwwill be replaced. Otherwise, the calculations in (1) are repeated with replacement ofXbbyXg.

If no improvement occurs in this case, a new solution is randomly generated within the feasible space to replace the worst frogXw. Then, the calculations continue for a specific number of iterations. After a prespecified number of memetic evolutionary steps within each memeplex, to ensure global exploration, ideas passed within memeplexes are combined in the shuffling process. All the frogs are resorted, and the population is redivided intommemeplexes. The concurrently implemented local search and global shuffling continue alternatively until predefined convergence criteria are satisfied.

3.2 SFLA_based optimization model

To achieve the minimum variance of the load profile including the load generated by EV battery swapping stations in one area, the position of the virtual frog consists of the charging or discharging power of each battery in each section. Based on Eq. (13), the charging power in the last section could be derived by the powers in other sections. It indicates that the number of independent variable of theithbattery istout(i)-tin(i)-2. Then the position vector of frog can be defined as

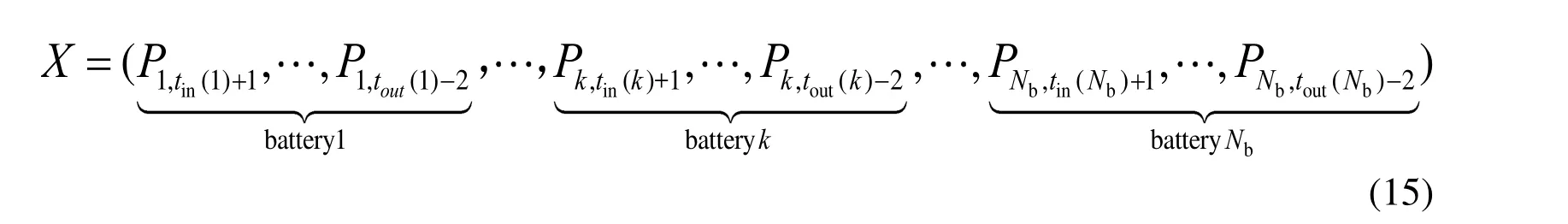
And the dimensionDof the vector is

Then the updating rule of position on each dimension within each memeplex could be expressed as

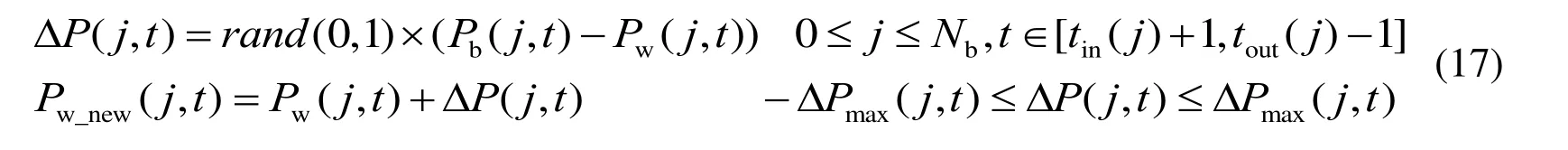
wherePb(j,t) andPw(j,t) represent thePj,tof the best and worst frog position vectors within a memeplex respectively;Pw_new(j,t) represents the updated power. If there is a batter fitness withPw_new(j,t), replacePwwithPw_new(j,t). Otherwise, usePg(j,t), which is thePj,tof the best frog position vector within the whole population, to replacePb(j,t) and repeat iterative update. If there is still no improvement, randomly generate aPw_new(j,t) and substitute the originalPw(j,t) for further iteration.

3.3 Steps of SFLA

The overall process of SFLA consists of the following main steps.

Step 1: Initialize the parameters, which include the number of frogs (p) in the whole population, the number of frogs (n) in each memeplex, the maximum iteration number(ite_m) for each memeplex and the maximum shuffling iteration number (ite_p) for the whole population. Obviously, the whole population is divided intom(p/n) memeplexes.Step 2: Initialize the population, which is formed by p randomly generated frogsX1,X2, . . . ,Xp. Compute the fitness value F(Xi) according to (2) for each frogXi. It is noted that in the position vectorX, the dimension of every battery is various, and it is relatively difficult to deal withX1,X2, . . . ,Xp. Therefore, we set the power to “0” in those non-effective sections those are beforetin(i) + 1 and aftertout(i) -1. Then every battery has the same dimension ofMb. As a result, the position vector of frog can be modified as

Step 3: Shuffle the frogs. Firstly, sort the p frogs in order of decreasing fitness, and then partition all frogs into m memeplexes. The first frog goes to the first memplex, the second frog goes to the second memeplex, themthfrog goes to themthmemeplex, the (m+1)thfrog goes back to the first memeplex, and at last thepthfrog goes to themthmemeplex.Step 4: Memetic evolution. Repeat the following operations for ite_m times: Firstly find the worst frogXwand the best frogXbin each memeplex, then updateXwaccording to Eq.(17), and yieldXw_new. IfXw_newhas a better fitness, replaceXwbyXw_new. Otherwise, repeat the updated strategy withXgreplacingXb. If this still cannot produce a better solution,replace theXwby a randomly generated frog. In fact,Xw_newis obtained by updating theDpowers in Eq. (15). The updating flow chart of theithbattery is shown in Figure 1.

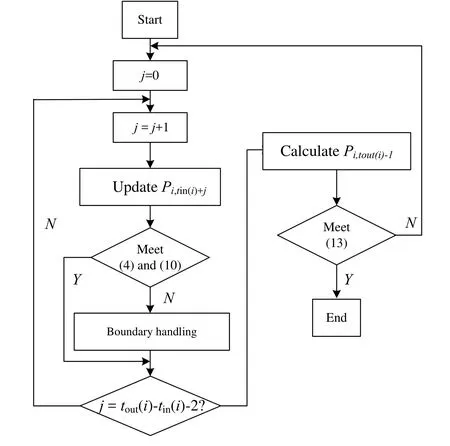
Figure 1: Updating flow chart of the ith battery

In Figure1, as much as possible in order to satisfy the constraint conditions of Eq. (13), if the updated charging power exceeds a certain boundary, absorption method is used to handle the boundary, setting the power to the boundary value; if the updated discharging power does, reflection method is applied to change (reduce) the power.

Step 5: Check convergence. If the convergence criteria are satisfied, stop and output the best frogXgin the whole population. Otherwise, return to Step 3.

Step 6: Output the results and quit the program.

Here, the convergence criteria are defined as the maximum number of shuffling iterations for whole population (ite_p).

4 Numerical simulation

In this paper, the optimization periodTois set to a day and divided into 24 sections with the durationTbof one hour.

4.1 Parameters of EV battery

In the EV market, there are different types such as NiMH, Lead Acid, and Li-Ion. And the market share of Li-Ion with its technical advantages has increased year by year. The“E6 pioneer” EV developed by BYD Co., Ltd., has been configured a Li-Ion battery with the energy density of 100W•h per kilogram (i.e., a battery of 600 kg can store power of 60 kW•h for each charging). Its main parameters are shown in Table 1.

Table 1: Basic parameters of battery

4.2 Area daily load

In a certain area, its daily load power regardless of EV swap station can be predicted and shown in Table 2.

4.3 Parameters of the EV battery swapping station

At the beginning of one optimization period, there are 600 batteries in the swapping station, including 350 full-charged batteries, 200 un-full changed batteries, and 50 reserved batteries. All batteries except the reserved batteries participate in the optimal control of coordinated charging. By predicting the demand of EV owners for swapping batteries during each optimization section, the number can be derived and shown in Table 3.

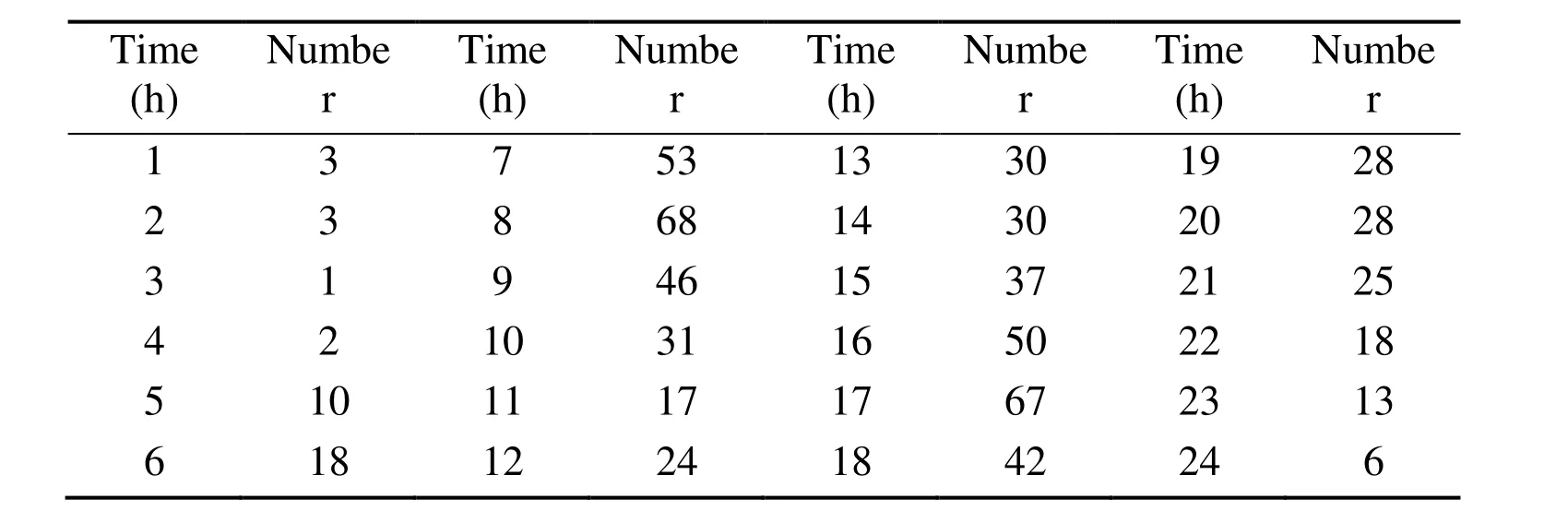
Table 3: Predicted number of batteries swapped in during each optimization section

4.4 Simulation and analysis

According to [Chen, Li and Hong (2015)], the maximum charging and discharging power of battery are set to 8 kW and 6 kW respectively, which are less than those of device.The main parameters of SFLA are shown in Table 4.

Table 4: Parameters of SFLA

Compared with the traditional one-way charging mode, the energy exchanging mode,bidirectional coordinated control has more efficient at smoothing the fluctuation of power load. Figure 2 shows the load profiles under various conditions and the variances are compared in Table 5.

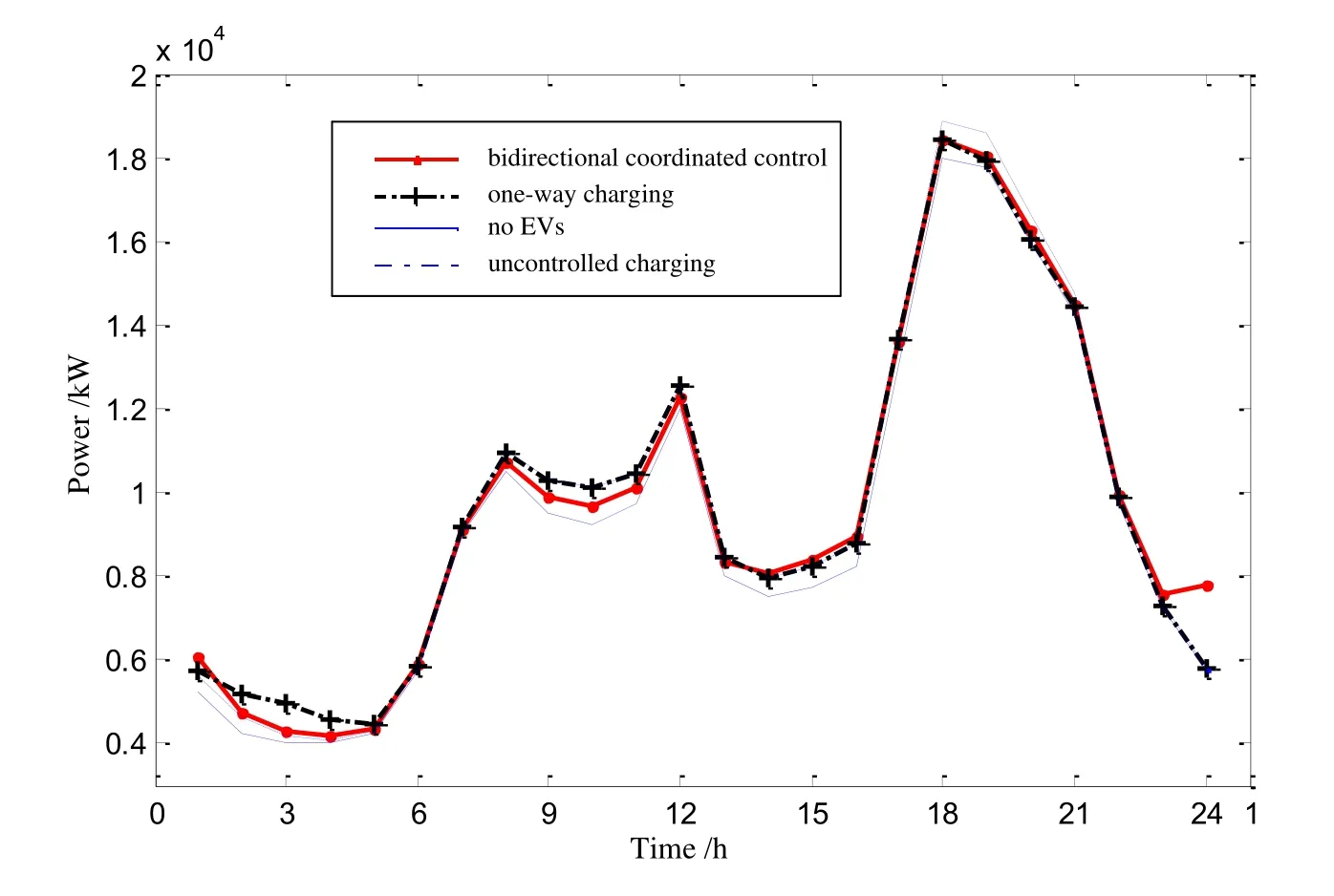
Figure 2: Area load profiles under different conditions

Table 5: Variances under different conditions

In Figure 2, the load profile under bidirectional coordinated control is the smoothest.Under this coordinated control, the batteries are recharged in the valley load time period and discharged in the peak load time period. During the daytime, the optimal load profile is closer to the profile of no EVs. And for making the swapping station the same state at the beginning of every optimization periodTo, there are many batteries which would be charged to full in the last section. Therefore, at the end ofTo, the charging power rises obviously. Fortunately, it happened in the night, which is the valley load time period.Furthermore, it is obvious that in Table 5 the coordinated charging can smooth the load fluctuation and shift peak load. And the variance has reduced from 1.836 × 107kW2to 1.538 × 107kW2in energy exchanging mode, which is more efficient to decline 16.23%,greater than that in one-way mode of 12.28%.

Particle swarm optimization (PSO) is usually used to solve optimization problems [Tian,Jing-Han and Jiang, et al. (2012); Han, He and Wang, et al. (2011); Rajanna and Saini(2016); Xuewei, Ke and Potter (2016)]. Then, the compared simulations are carried out with 200 particles and the results are shown in Figure 3.

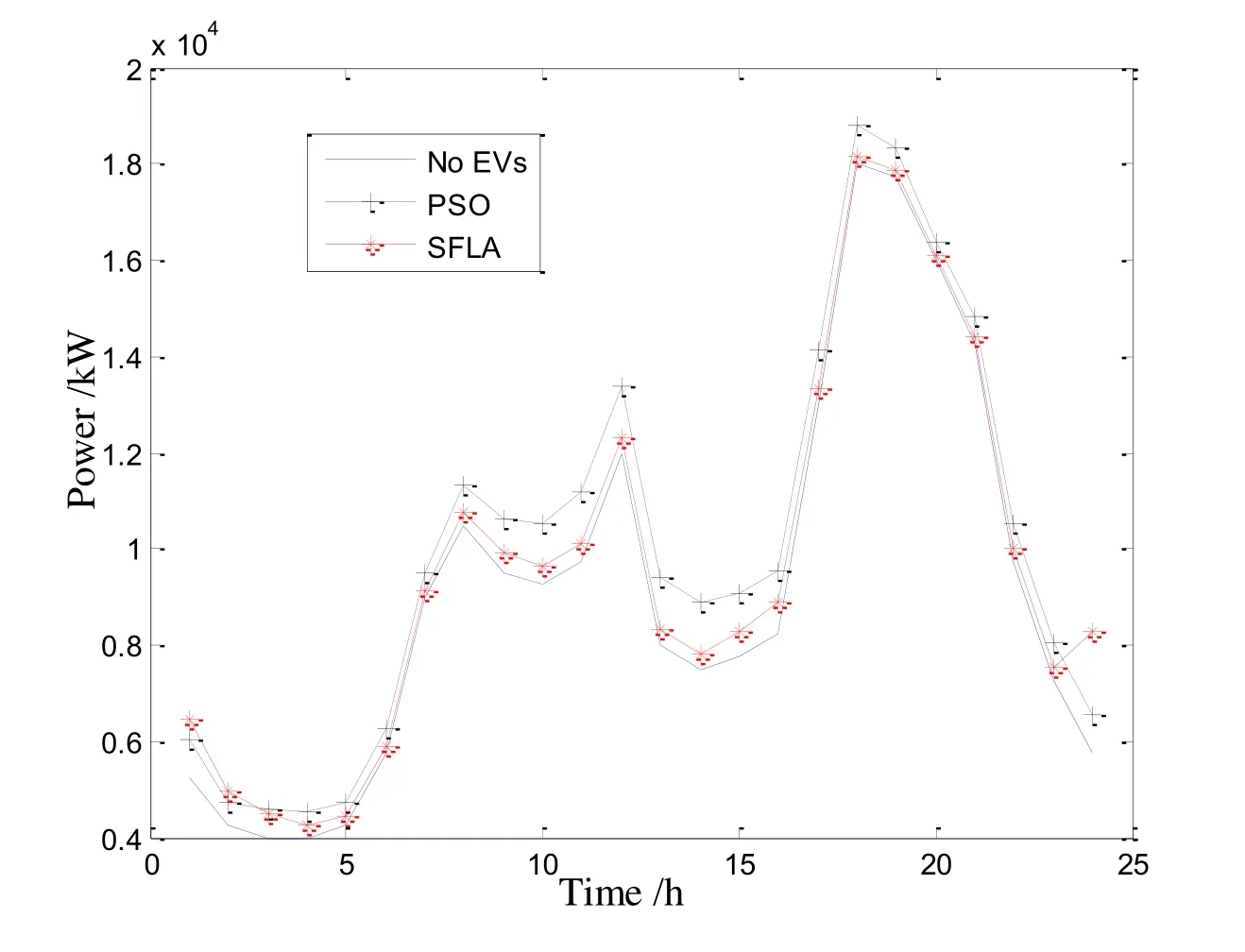
Figure 3: Area load profiles optimized with PSO and SFLA

In Figure 3, SFLA and PSO can lower the load peak-valley difference and smooth the load profile. But the convergence characteristics of two algorithms in the numerical simulation differ greatly and are shown in Figure 4.

Figure 4: Convergence characteristics of SFLA and PSO

Clearly, the convergence rate of SFLA is much faster (100) than that of PSO (more than 1000) and the minimum variance of the load profile generated by SFLA is less than that generated by PSO, shown in Table 6.

Table 6: Variances generated by PSO and SFLA

5 Conclusion

As a main way of energy supply to EVs, the optimal control strategy for coordinated charging of the swapping station is very important in smoothing the load profile.Considering bidirectional power flow between the station and power grid, this paper presented an optimization model of EV battery swapping station and proposed a SFLA-based control strategy to optimize the operation of station. Compared simulations were carried out and the main conclusions of this paper are as follows:

• For the swapping station, energy exchanging mode can supply energy for large-scale EVs with a smoother load profile than one-way charging mode.

• Compared to particle swarm optimization (PSO) method, the presented SFLA-based strategy can effectively lower the peak-valley difference with the faster convergence rate and higher convergence precision.

Conflict of Interests:The authors declare that there is no conflict of interests regarding the publication of this paper.

Aziz, M.; Oda, T.; Mitani, T.; Watanabe, Y.; Kashiwagi,T.(2015): Utilization of electric vehicles and their used batteries for peak-load shifting,Energies, vol. 8, pp.3720-3738.

Chen, C. F.; Li, H. Y.; Hong,C. W.(2015): Molecular dynamics analysis of high-temperature molten-salt electrolytes in thermal batteries,Computers Materials &Continua, vol. 46, pp. 145-163.

Du, J.; Wang, X.; Lv,H.(2016): Optimization of Magnet Shape Based on Efficiency Map of IPMSM for EVs,IEEE Transactions on Applied Superconductivity, vol. 26, pp.1-7.

Ebrahimi, J.; Hosseinian, S. H.; Gharehpetian,G. B.(2011): Unit Commitment Problem Solution Using Shuffled Frog Leaping Algorithm,IEEE Transactions on Power Systems, vol. 26, pp. 573-581.

Eusuff, M. M.; Lansey,K. E.(2003): Optimization of Water Distribution Network Design Using the Shuffled Frog Leaping Algorithm,American Society of Civil Engineers, vol. 129, pp. 210-225.

Han, H. Y.; He, J. H.; Wang, X. J.; Jiang, J. C.; Tian,W. Q.(2011): An Improved Particle Swarm Optimization-Based Load Response Strategy with Participation of Vehicle to Grid, Power System Technology, vol. 35, pp. 165-169. (In Chinese)

Huang, X.; Qiang, H.; Zhang, Q. D.; Li,H.(2013): Research on ISFLA-Based Optimal Control Strategy for the Coordinated Charging of EV Battery Swap Station,Mathematical Problems in Engineering, vol. 2, pp. 1-7.

Kang, Q.; Wang, J. B.; Zhou, M. C.; Ammari,A. C.(2016): Centralized charging strategy and scheduling algorithm for electric vehicles under a Battery swapping scenario,IEEE Transactions on Intelligent Transportation Systems, vol. 17, pp.659-669.

Qiang,H.(2015): Research on the Impacts of EVs Involving Wireless Charging Mode on the Power Grid, Southeast University. (In Chinese)

Rajanna, S.; Saini,R. P.(2016): Employing demand side management for selection of suitable scenario-wise isolated integrated renewal energy models in an Indian remote rural area,Renewable Energy, vol. 99, pp. 1161-1180.

Sun, L.; Wang, X.; Liu, W.; Lin,Z.(2015): Optimization model for power system restoration with support from electric vehicles employing battery swapping,Iet Generation Transmission & Distribution, vol. 10, pp. 771-779.

Tian, W. Q.; Jing-Han, H. E.; Jiang, J. C.; Niu, L.Y. and Wang, X.J.(2012):Research on dispatching strategy for coordinated charging of electric vehicle battery swapping station,Power System Protection & Control.

Tan, K. M.; Ramachandaramurthy, V. K; Yong, J. Y.(2016): Optimal vehicle to grid planning and scheduling using double layer multi-objective algorithm, Energy, vol.112, pp. 1060-1073.

Vahedipour-Dahraie, M.; Rashidizaheh-Kermani, H.; Najafi,H. R.(2017): Coordination of EVs Participation for Load Frequency Control in Isolated Microgrids, Applied Sciences, vol. 7, pp. 1-16.

Williams, J. H., DeBenedictis, A.; Ghanadan, R.; Mahone, A.; Moore, J.; Morrow,

W. R.; Price, S; Torn, M. S.(2012): The technology path to deep greenhouse gas emissions cuts by 2050: The pivotal role of electricity,Science, vol. 335, pp. 53-59.

Xuewei, Q. I.; Ke, L. I; Potter,W. D.(2016): Estimation of distribution algorithm enhanced particle swarm optimization for water distribution network optimization,Frontiers of Environmental Science & Engineering, vol. 10, pp. 341-351.

Xia, M.; Lai, Q.; Zhong, Y.; Li, C; Chiang,H.(2016): Aggregator-based interactive charging management system for electric vehicle charging,Energies, vol. 9, pp. 159.

Xie, P.; Li, Y.; Zhu, L; Shi,D.Supplementary automatic generation control using controllable energy storage in electric vehicle battery swapping stations,Iet Generation Transmission & Distribution, vol. 10, pp. 1107-1116, 2016.

Yang, J; Sun,H.(2015): A hybrid genetic algorithm for battery swap stations location and inventory problem,International Journal of Shipping & Transport Logistics, vol. 7,pp. 246-265.

Yang, Y.; Zhang, W.; Niu, L; Jiang,J.(2015): Coordinated charging strategy for electric taxis in temporal and spatial scale,Energies, vol. 8, pp. 1256-1272.

Zhang, Q. D.; Huang, X. L.; Chen, Z.; Chen, L. X.; Xu,Y. P.(2015): Research on control strategy for the uniform charging of electric vehicle battery swapping station,Diangong Jishu Xuebao/transactions of China Electrotechnical Society, vol. 30, pp.447-453. (In Chinese)

Zhao, G.; Huang, X; Qiang, H.(2015): Coordinated control of PV generation and EVs charging based on improved DECell algorithm,Int. J. Photoenergy, pp. 1-13.

Zhang, S.; Zhang, C.; Xiong, R; Zhou,W.(2014): Study on the optimal charging strategy for lithium-ion batteries used in electric vehicles,Energies, vol. 7, pp. 6783-6797.