Comparison of CS, CGM and CS-CGM for Prediction of Pipe’s Inner Surface in FGMs

Haolong Chen, Bo Yu, Huanlin Zhou＊ and Zeng Meng

1 Introduction

In the past several decades, inverse heat conduction problem has been widely applied in the field of science and engineering [Alifanov (1994); Taler and Duda (2006)], such as identification of the boundary conditions [Lee, Lai and Chen et al. (2013); Fu, Chen and Zhang (2012)], thermo-properties [Chen, Chen, and Wei (2015)] and geometry of the boundary [Chen, Cao and Wang et al. (2016)] from the knowledge of the temperature measurements taken in the domain or on the surface. The inverse geometry problem(IGP) has broad application in geometry optimization [Naumann, Evans and Walton et al.(2016)], biological lesion detection [Partridge and Wrobel (2007)], radar cross section estimation [Girish and Hema (2016)] and inner surface prediction [Cheng and Chang(2003)]. In the field of engineering, the identification of a pipe’s inner-surface shape is of great importance [Fan, Sun and Yang (2007); Mohamed and Marcel (2017)].Functionally graded materials (FGMs) have attracted many research interests in materials and engineering sciences [Sladek, Sladek and Zhang (2004); Li, Guo and Zhang et al. (2015); Zhang, Yu and Zhang et al. (2015); Wu and Jiang (2015)]. However,the study on the IGP of FGMs is limited in the literature.

Compared with other numerical methods, the boundary element method (BEM) is an effective way to solve the IGP Li, Wang, Chen, Zhu and Zhang (2016)]. The advantage of the BEM to identify boundary shape is that only the boundary is needed to be discretized into elements, which can reduce dimensions and keep accuracy [Sun, Huang,Liu and Cen (2004)]. However, the BEM faces a serious challenge when solving non-linear, non-homogeneous and transient problems since there are domain integrals in the resulting integral equations [Abreu, Canelas and Mansur (2013); Tadeu, Prata and Simõ es (2015); Yu, Zhou and Chen et al. (2015)], thus making the BEM lose its advantage of boundary only discretization. To overcome this shortcoming, the dual reciprocity method (DRM) [Partridge, Brebbia and Wrobel (1992)] and the radial integral method (RIM) [Gao (2002)] have been developed to transform the domain integral into the boundary integral. The RIM can not only transform any complicated domain integrals to the boundary without using the particular solution, but also remove the various singularities appearing in the domain integrals [Gao (2005)]. The method combining RIM with BEM (RIBEM) has been used in non-linear and non-homogeneous elastic problems [Gao, Zhang and Luo (2007)], the heat conduction problems[AL-Jawary and Wrobel (2012)] and thermoelastic problems [Gao, Zheng and Yang et al.(2015)]. Moreover, the boundary particle method [Fu, Chen and Yang (2013)] is suitable to solve the nonhomogeneous problem.

The IGP can be regularized by a series of regularization algorithms, such as the Tikhonov regularization method, the Levenberg-Marquardt method (LMM) and the conjugate gradient method (CGM). Karageorghis, Lesnic and Marin (2015) solved the direct and inverse Signorini problems by using the method of fundamental solution. Wang, Lin and Yang (2015)estimated the geometry boundary for the inner surface in a furnace wall made of FGMs by CGM and finite element method. Kazemzadeh-Parsi and Daneshmand (2013) identified the inner wall of pipeline by using smoothed fixed grid finite elements. Fan, Sun and Yang (2007)identified a pipeline’s irregular inner boundary by the CGM. Hafid and Lacroix (2017)predicted the state of the brick wall of a melting furnace by using the LMM and Broyden method. Different optimization algorithms were also used and compared by Rus and Gallego(2002). Sun, Hong and Zhao et al. (2016) solved the IGP of a two-dimensional radiative enclosure filling with participating media by the krill herd algorithm.

Generally, many gradient optimization methods have been suggested to solve the IGP, in which LMM and CGM are widely utilized owing to their stable, powerful and efficient characteristics [Huang and Liu (2010)]. However, LMM and CGM are locally convergent and the results are sensitive to the initial values. In practical engineering, it is not convenient to get exact initial values. Especially for complex boundary shape and many observation points, those gradient type algorithms lose efficacy.

In the past several years, evolutionary algorithms have developed quickly and become a hot topic in structure optimization domain. In 2009, Yang and Deb (2009) proposed cuckoo search algorithm(CS). The CS has advantages of good global search capability and few control parameters factors. Yang and Deb (2010) applied the CS to solve engineering optimization problems, such as the design of springs and welded beam structures. Up to now, the CS has been widely used in hydrothermal scheduling problems[Nguyen, Vo and Truong (2014)], aerodynamic shape optimizations [Naumann, Evans and Walton (2015)] and reliability optimization problems [Valian, Tavakoli and Mohanna et al. (2013)]. It should be noted that although the CS has good global search ability, its convergence speed is very slow because it does not utilize the gradient information. Thus,it is difficult to apply the CS to complex engineering model due to the unbearable computational cost.

In this paper, the CS is improved by using the CGM, and the CS-CGM is proposed. The CS,CGM and CS-CGM are used and compared to predict a pipe’s inner surface in FGMs. A brief outline of the paper is as follows: firstly, the direct problem is solved by RIBEM in Section 2 and the objective function of the inverse problem is proposed in Section 3. The theories of the CS and the CGM are presented and the flowchart of the CS-CGM is shown in Section 4. In addition, numerical examples are presented in Section 5. Finally, some conclusions are drawn in Section 6.

2 Direct problem

2.1 The governing equation

A cross sectional schematic of a pipeline with an irregular inner boundary is displayed in Fig. 1. The governing equation for two-dimensional transient heat conduction problems in FGMs is given as follows

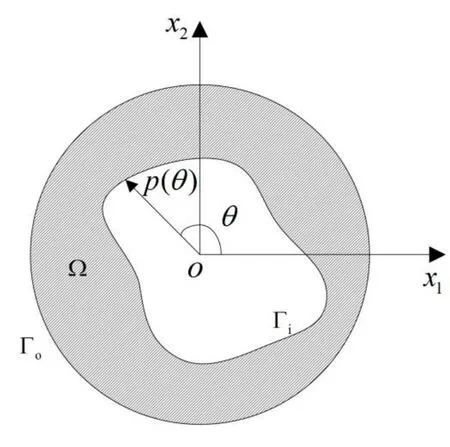
Figure 1: Geometry model

2.2 The direct problem

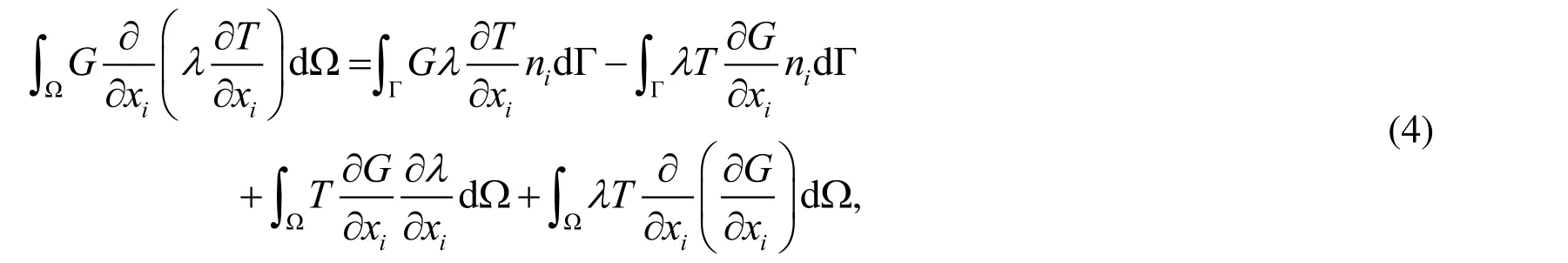
whereris the distance between the source pointand the field point.

Using the property of Dirac delta function, the last domain integral of Eq. (4) can be written as

Substitute Eq. (7) into Eq. (4) and the result into Eq. (3)

There are two domain integrals involved in Eq. (8). The domain integrals can be transformed into boundary integrals by using the RIM. Using a collocation technique, a system equation can be obtained

3 Inverse problem

As shown in Fig. 1, all boundary conditions are known except the shape of inner boundary. The purpose is to identify the boundary shape based on the measured temperature and the computed temperatureˆ. It should be noted that the measured temperaturecontains measurement noises.

The solution of the present problem is transformed to find a boundary shapeby minimizing the objective function

wherewis the number of measurement timepoints (the important moments among the whole computation time) andmis the number of measurement points. The basic principle of selecting the timepoints is that if the temperature of measurement points changes obviously during a time interval, the timepointis selected. The values ofcan be obtained by solving the direct problem with the estimated boundary shape

As the unavoidable measurement noises or the numerical computing errors, the first order regularization can be used to avoid instabilities in the estimated values. The objective function is defined as

wherenis the number of observation points.is the regularization parameter, which can minimize the instabilities and effect of noisy data. Selection of an appropriate value ofis crucial for the shape identification problems. L-shape curve method is suitable for obtaining the regularization parameter [Udayraj, Mulani and Talukdar et al. (2015)].

4 CS-CGM method

4.1 CS algorithm

The CS is a metaheuristic algorithm by mimicking cuckoos. The aggressive behavior of cuckoos is that they lay eggs in the nests of other species [Payne and Sorensen (2005)].Therefore, it has a chance that the host of the nest will discover the cuckoo’s eggs and abandon the eggs or nest. So, some cuckoo species simulate the eggs of the host nest in color or in pattern. This reduces the possibility of the dropped eggs and increases their reproductively.

Usually, there are three idealized rules in the CS:

(1) A laid egg by each cuckoo puts in an arbitrarily selected nest at a time;

(2) The next generations go on with the best nests (good quality eggs);

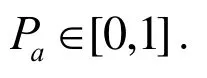
The purpose of the CS is to findwhich minimizes the objective functionThe new solutioncan be obtained by the above equations for thek-th iteration

Usually, the foraging behavior of animals is random or quasi-random and the behavior has demonstrated the characteristics of Lé vy flight. The random walk and step can be generated by the Lé vy flight according to the distribution

whereuis the normal stochastic variable,kis the number of iterations.

In order to generate random numbers which obey Lé vy flights, a step size and a random direction must be computed by the given Lé vy distribution. The step can be expressed as

vis the normal stochastic variable.uandvobey the normal distribution and can be written as

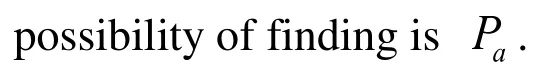
4.2 Conjugate gradient method

The iterative process based on the CGM to solve the IGP can be expressed as follows

In this paper, the following stopping criterion is taken for the inverse problem(31)

4.3 CS-CGM method

Although the CS is a novel global optimization method, the convergence speed of the CS is very slow because the search direction and iteration step do not utilize the gradient information. In this paper, the method combining the CS with the CGM is proposed to identify the pipe’s inner surface. After implement of Lé vy flights and elimination mechanism, the values of objective function are decreased rapidly by using the CGM. As a result, the local search ability of the CS-CGM method is significantly strengthened.

The computation process of the CS-CGM for solving the shape identification problem is summarized and the flowchart is shown in Fig. 2.

Figure 2: The flowchart of the CS-CGM

5 Numerical example

Four numerical examples are presented to prove the accuracy and effectiveness of the three methods in this section. In order to compare the results with random measurement noises, normally distributed uncorrelated errors with zero and constant standarddeviation are assumed. The measurement temperature can be expressed as

As shown in Fig. 3, the outer radius is 2m. The temperature of the outside environment and the initial temperature are given as. The heat is transferred from the outer surface to the air by natural convection and the temperature distribution on the inner boundary isatt=0. The coefficient of convective heat transferspecific heatdensity. The direct problem is solved by the RIBEM. The inner and outer boundaries are divided into 16 linearelements, respectively. The whole computation time is 200s and the timeinterval is. 16 observation points are chosen coinciding with the corresponding nodes of 16 linear elements on the inner boundary. And the measurement points are uniformly located on the cycleR=1.8m. The stopping criterion is taken as.

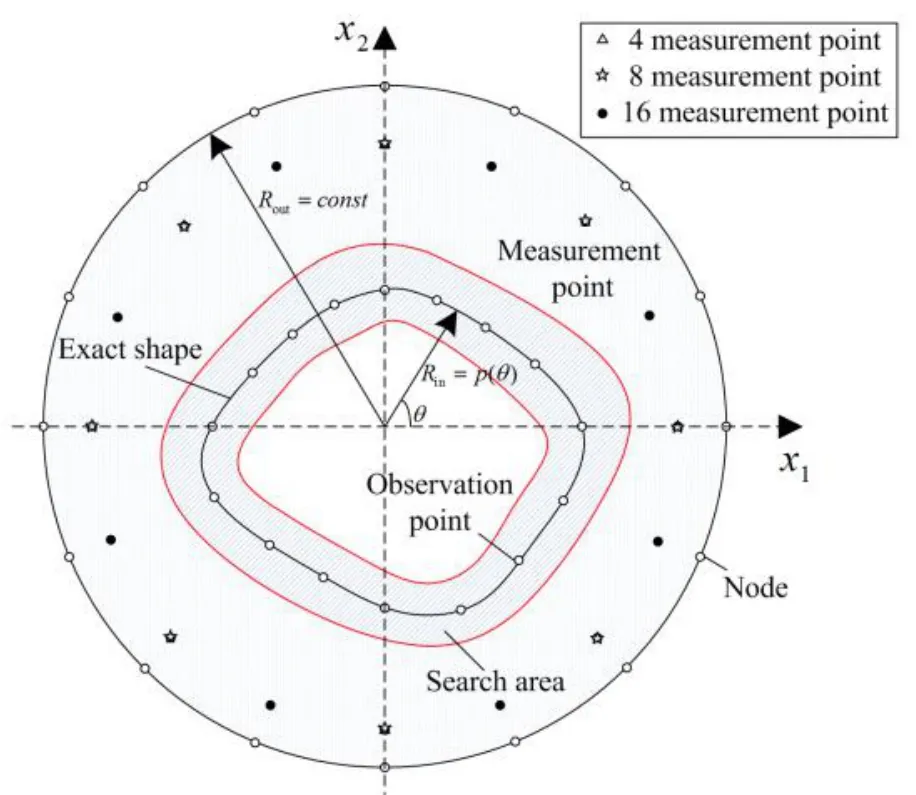
Figure 3: BEM model of the pipe

5.1 Circle inner boundary

The exact shape of the inner wall in this example is a cycle with the radiusR=1m. And the thermal conductivity

5.1.1 The effect of initial guess

The problem is solved by the CS, CGM and CS-CGM with different initial values. In this case, the number of measurement timepoints is taken as 2. The inverse results are listed in Tab. 1. It can be seen that when the initial boundary shape is closer to the exact shape, satisfactory results can be obtained by the CGM. However, the results of the CGM are very sensitive to the initial values and the CGM cannot converge when the initial value is taken as 0.5 or 1.5. In the CS and CS-CGM, the initial values are generated by the random numbers from 0.3 to 1.5. The CS-CGM can obtain satisfactory results by less iteration number. However, the CS needs more iterations and costs more computation time. The results show that the CS-CGM has higher convergence efficiency than the CS and the CGM.

Table 1: Comparison of CS, CGM and CS-CGM.

5.1.2 The effect of the number of measurement timepoints

For comparison, the numbers of measurement timepoints are taken as 1, 2 and 4,respectively. The inverse results of the CS, CGM and CS-CGM are shown in Fig. 4 and the AREs are listed in Tab. 2.

Figure 4: Inverse results with different timepoints

Table 2: AREs for different timepoints

From Fig. 4, it can be seen that the CS, CGM and CS-CGM can identify the pipe’s inner surface with different numbers of timepoints. As the number of timepoints increases, the estimated shape is closer to the exact shape. The results of the CGM and CS-CGM are better than the CS. Tab. 2 shows that with the increase of number of timepoints, the AREs are getting smaller. Next, the number of measurement timepoints is taken as 2.

5.2 Eccentric circle inner boundary

In this example, the inner boundary shape is an eccentric circle with

5.2.1 The effect of the number of measurement points

As shown in Fig. 3, the numbers of measurement points are taken asm=4, 8 and 16. The inverse results obtained by the CS, CGM and CS-CGM are shown in Fig. 5 and the AREs are listed in Tab. 3.

Figure 5: Inverse results with different measurement points

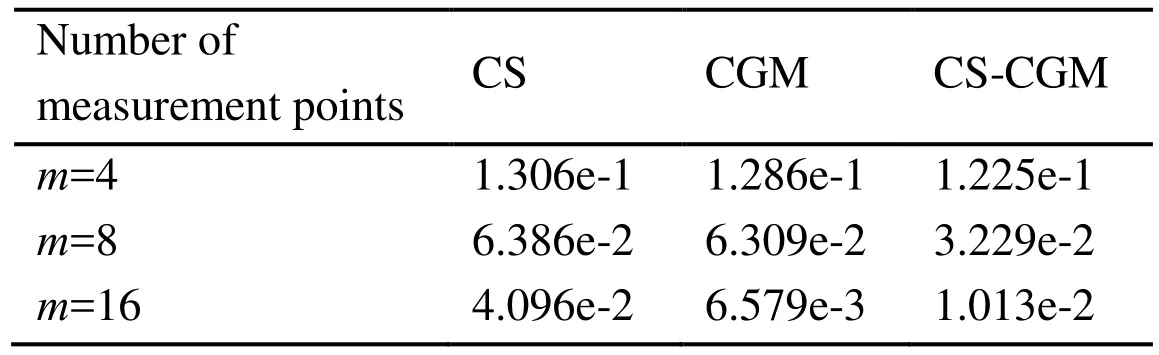
Table 3: AREs for different measurement points

From Fig. 5, it is clear that when the number of measurement pointsm=4, only the CS-CGM can get accurate results. When the number of measurement points is taken as 16, the results obtained by the CGM and CS-CGM are better than the CS. It is clear to see that as the number of measurement points increases, the inverse shape is closer to the exact shape. Tab.3 shows that the AREs decrease with the increase of measurement point number.

5.2.2 The effect of random noises

In order to test the stability of the three methods, the measurement noises are taken as 1.0%, 2.0% and 3.0%. For comparison, the number of measurement points is taken asm=16. The inverse results with different measurement noises are exhibited in Fig. 6. Tab.4 provides the AREs corresponding to the measurement noises.

Figure 6: Inverse results with different measurement noises

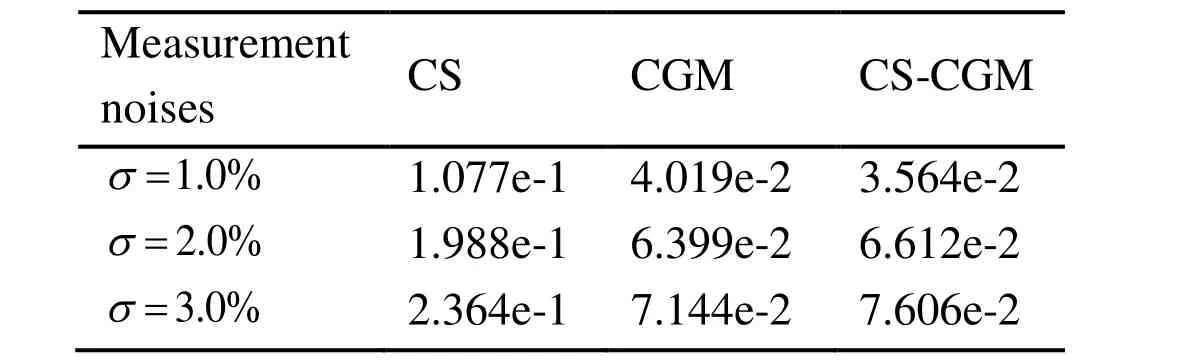
Table 4: AREs for different measurement noises

From Fig. 6, it is found that with the increase of measurement noises, the results are diverging from the exact shape. When the measurement noise is taken as 3.0%, the results of the CS-CGM are better than the CS. As shown in Tab. 4, with the decrease of measurement noises, the AREs are getting smaller. It is clear to see that the results obtained by the CS algorithm are more sensitive to the measurement noises than the CGM and CS-CGM.

5.3 The nephroid inner boundary

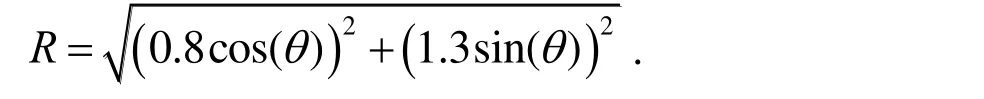
5.3.1 The effect of the number of measurement points

In this case, the numbers of measurement points are also taken as 4, 8 and 16. The inverse results of the CS, CGM and CS-CGM are shown in Fig. 7. It is clear that the CS,CGM and CS-CGM can identify the inner shape. The results get more accurate as the measurement points increase. When sufficient measurement information is used,satisfactory results can be obtained.

The AREs with different number of measurement points are also computed and listed in Tab. 5. With the increase of number of measurement points, the inverse results are closer to the exact ones and the AREs get smaller. It shows that the results obtained by the CS-CGM are more accurate than the CS and CGM.

Figure 7: Inverse results with different measurement points

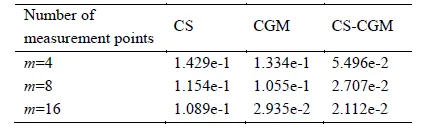
Table 5: AREs for different measurement points

5.3.2 The effect of random noises

The measurement noises are taken as 1.0%, 2.0% and 3.0%. In this case, 16 measurement points are considered. The inverse results with different measurement noises are displayed in Fig. 8. Tab. 6 provides the AREs corresponding to the measurement noises.

From Fig. 8, it is found that with the increase of measurement noises, the results are diverging from the exact shape. When the measurement noise is taken as 3.0%, the results obtained by the CS-CGM are better than the CS and CGM. As shown in Tab. 6,with the decrease of measurement noises, the AREs are smaller and the estimated shape is closer to the exact one. The results show that the measurement noise has less effect on the results of the CGM and CS-CGM.

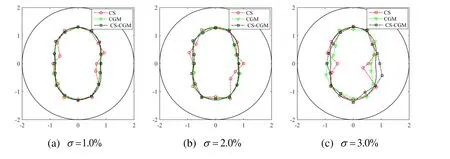
Figure 8: Inverse results with different measurement noises

Table 6: AREs for different measurement noises

5.4 The square inner boundary

5.4.1 The effect of the number of measurement points

In this case, three different kinds of measurement points are also considered. The inverse results of the CS, CGM and CS-CGM are shown in Fig. 9. The AREs with different measurement points are given in Tab. 7.

From Fig. 9, it is clear that the CS, CGM and CS-CGM can identify the inner shape with 16 measurement points. As listed in Tab. 7, with the increase of number of measurement points, the inverse results are closer to the exact ones and the AREs get smaller. It shows that the results obtained by the CS-CGM are more accurate than the CS and CGM.

Figure 9: Inverse results with different measurement points

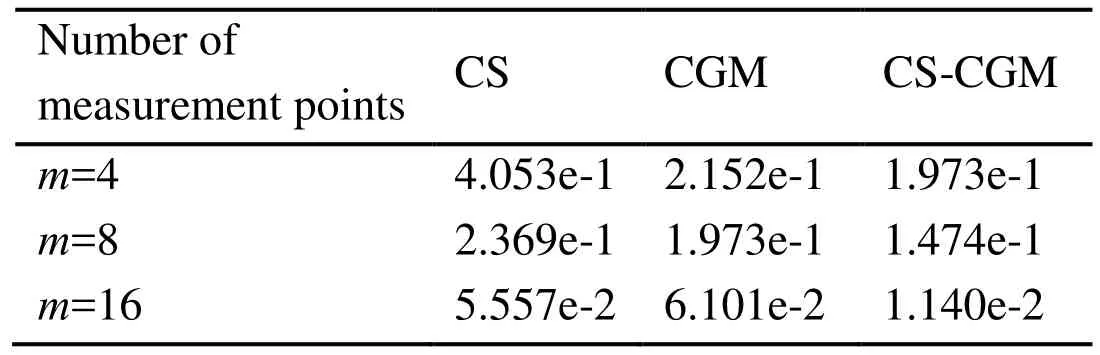
Table 7: AREs for different measurement points

5.4.2 The effect of random noises

The measurement noises are also taken as 1.0%, 2.0% and 3.0%. 16 measurement points are used. The inverse results are displayed in Fig. 10. Tab. 8 provides the AREs.

From Fig. 10, it is found that with the increase of measurement noises, the results are diverging from the exact shape. When the measurement noise is taken as 3.0%, the results obtained by the CS-CGM are better than the CS and CGM. As shown in Tab. 8,with the decrease of measurement noises, the AREs are smaller and the estimated shape is closer to the exact one.

Figure 10: Inverse results with different measurement noises

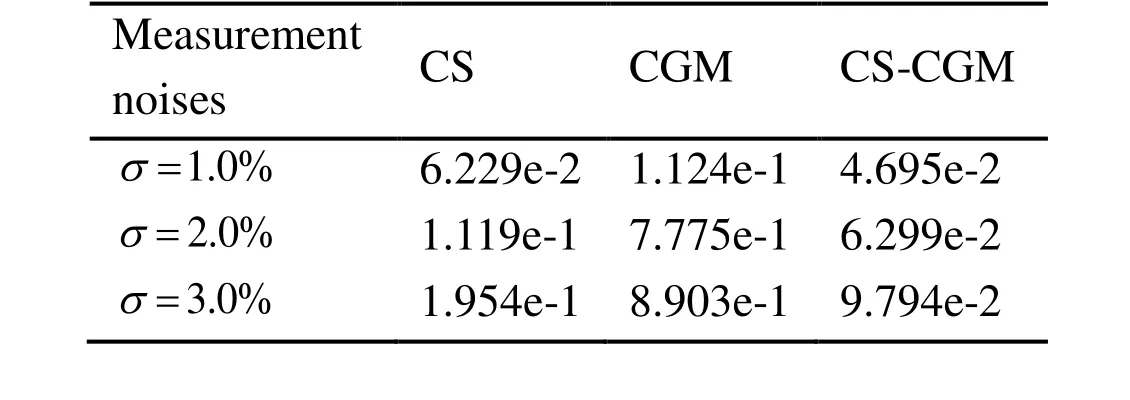
Table 8: AREs for different measurement noises

6 Conclusion

In this paper, the CS is improved by the CGM, and the CS-CGM is proposed. The CS, CGM and CS-CGM are used to predict a pipe’s inner-surface in FGMs. The unknown boundary shapes are generated randomly and evolved by Lé vy flights and elimination mechanism for the CS and CS-CGM. Then the CGM is adopted to minimize the objective function. The influences of the number of measurement timepoints, measurement points and the random measurement noises on the inverse results are also discussed. It is observed that all the three algorithms are able to estimate the unknown inner boundary shape of the pipe. The computational efficiency of the CS, CGM and CS-CGM is also compared. The followings are the major conclusions:

(1) The three methods can perform in the case of noiseless measurements for prediction of a pipe’s inner surface.

(2) The results obtained by the CS are more sensitive to the measurement noises compared with the CGM and CS-CGM. To get accurate results, the CS needs more iteration numbers.

(3) The CGM has good performance in the identification of the pipe’s inner surface. But the CGM is very sensitive to initial values.

(4) The CS-CGM has the best efficiency and the fastest convergence speed among the three methods.

(5) With the increase of timepoints and measurement points, and with the decrease of measurement noise, the inverse results are more accurate.

It can be concluded that the CS-CGM is better than the CS and CGM. Therefore, the CS-CGM can be used to satisfactorily identify the inner shape of a pipe in engineering.

Acknowledgements:The research is supported by the National Natural Science Foundation of China (Nos. 11672098, 11502063) and the Natural Science Foundation of Anhui Province(No. 1608085QA07).

Alifanov, O. M.(1994):Inverse heat transfer problems, Springer-Verlag, Berlin Heidelberg.

Abreu, A. I.; Canelas, A.; Mansur, W. J.(2013): A CQM-based BEM for transient heat conduction problems in homogeneous materials and FGMs.Applied Mathematical Modelling, vol. 37, pp. 776-792.

AL-Jawary, M. A.; Wrobel, L. C.(2012): Radial integration boundary integral and integro-differential equation methods for two-dimensional heat conduction problems with variable coefficients.Engineering Analysis with Boundary Elements, vol. 36, pp. 685-695.

Cheng, C. H.; Chang, M. H.(2003): Shape identification by inverse heat transfer method.Transactions-American Society of Mechanical Engineers Journal of Heat Transfer, vol. 125,pp. 224-231.

Chen, B.; Chen, W.; Wei, X.(2015): Characterization of space-dependent thermal conductivity for nonlinear functionally graded materials.International Journal of Heat and Mass Transfer, vol. 84, pp. 691-699.

Chen, H.; Cao, D. M.; Wang, G. J.; Wan, S. B.; Li, Y. H.(2016): Fuzzy estimation for unknown boundary shape of fluid-solid conjugate heat transfer problem.International Journal of Thermal Sciences. vol. 106, pp. 112-121.

Fu, Z. J.; Chen, W.; Yang, H. T.(2013): Boundary particle method for Laplace transformed time fractional diffusion equations.Journal of Computational Physics, vol.235, pp. 52-66.

Fu, Z. J.; Chen, W.; Zhang, C. Z.(2012): Boundary particle method for Cauchy inhomogeneous potential problems.Inverse problems in Science and Engineering, vol.20, pp. 189-207.

Fan, C. L.; Sun, F. R.; Yang, L.(2007): An algorithm study on the identification of a pipeline’s irregular inner boundary based on thermographic temperature measurement.Measurement Science and Technology, vol. 18, pp. 2170-2177.

Gao, X. W.(2002): The radial integration method for evaluation of domain integrals with boundary-only discretization.Engineering Analysis with Boundary Elements, vol.26, pp. 905-916.

Gao, X. W.(2005): Evaluation of regular and singular domain integrals with boundary-only discretization-theory and Fortran code.Journal of Applied Mathematics and Computing, vol.175, pp. 265-290.

Girish, K.; Hema, S.(2016):Analytical estimation of radar cross section of infinitely long conducting cylinder coated with metamaterial.Computers, Materials & Continua,vol. 52, pp. 193-211.

Gao, X. W.; Zhang, C.; Guo, L.(2007): Boundary-only element solutions of 2D and 3D nonlinear and nonhomogeneous elastic problems.Engineering Analysis with Boundary Elements, vol. 31, pp. 974-982.

Gao, X. W.; Zheng, B. J.; Yang, K.; Zhang, C.(2015): Radial integration BEM for dynamic coupled thermoelastic analysis under thermal shock loading.Computers &Structures, vol. 158, pp. 140-147.

Huang, C. H.; Liu, C. Y.(2010): A three-dimensional inverse geometry problem in estimating simultaneously two interfacial configurations in a composite domain.International Journal of Heat and Mass Transfer, vol. 53, pp. 48-57.

Hafid, M.; Lacroix, M.(2017): Inverse heat transfer prediction of the state of the brick wall of a melting furnace.Applied Thermal Engineering, vol. 110, pp. 265-274.

Kazemzadeh-Parsi, M. J.; Daneshmand, F.(2013): Inverse geometry heat conduction analysis of functionally graded materials using smoothed fixed grid finite elements.Inverse Problems in Science and Engineering, vol. 21, pp. 235-250.

Karageorghis, A.; Lesnic, D.; Marin, L.(2015): The method of fundamental solutions for solving direct and inverse Signorini problems.Computers & Structures, vol. 151, pp. 11-19.Li, G. Y.; Guo, S. P.; Zhang, J. M.; Li, Y.; Han, L.(2015): Transient heat conduction analysis of functionally graded materials by a multiple reciprocity boundary face method.Engineering Analysis with Boundary Elements, vol. 60, pp. 81-88.

Lee, H. L.; Lai, T. H.; Chen, W. L.; Yang, Y. C.(2013): An inverse hyperbolic heat conduction problem in estimating surface heat flux of a living skin tissue.Applied Mathematical Modelling, vol. 37, pp. 2630-2643.

Li, Y. H.; Wang, G. J.; Chen, H.; Zhu, Z. Y.; Zhang, D. Q.(2016): A decentralized fuzzy inference method for the inverse geometry heat conduction problem.Applied Thermal Engineering, vol. 106, pp. 109-116.

Naumann, D. S.; Evans, B.; Walton, S.; Hassan, O.(2015): A novel implementation of computational aerodynamic shape optimisation using modified cuckoo search.Applied Mathematical Modelling, vol. 40, pp. 4543-4559.

Naumann, D. S.; Evans, B.; Walton, S.; Hassan, O.(2016): A novel implementation of computational aerodynamic shape optimisation using modified cuckoo search.Applied Mathematical Modelling, vol. 40, pp. 4543-4559.

Nguyen, T. T.; Vo, D. N.; Truong, A. V.(2014): Cuckoo search algorithm for short-term hydrothermal scheduling.Applied Energy, vol. 132, pp. 276-287.

Partridge, P. W.; Brebbia, C. A.; Wrobel, L. C.(1992): The dual reciprocity boundary element method, Computational Mechanics Publication, Southampton.

Payne, R. B.; Sorensen, M. D.(2005):The cuckoos, Oxford University Press, Oxford.

Partridge, P. W.; Wrobel, L. C.(2007): An inverse geometry problem for the localisation of skin tumours by thermal analysis.Engineering Analysis with Boundary Elements, vol. 31,pp. 803-811.

Rus, G.; Gallego, R.(2002): Optimization algorithms for identification inverse problems with the boundary element method.Engineering Analysis with Boundary Elements, vol. 26,pp. 315-327.

Sun, X. S.; Huang, L. X.; Liu, Y. H.; Cen, Z. Z.(2004): Elasto-plastic analysis of two-dimensional orthotropic bodies with the boundary element method.Computers, Materials& Continua, vol. 1, pp. 91-105.

Sladek, J.; Sladek, V.; Zhang, C.(2004): A local BIEM for analysis of transient heat conduction with nonlinear source terms in FGMs.Engineering Analysis with Boundary Elements, vol. 28, pp. 1-11.

Sun, S. C.; Hong, Q.; Zhao, F. Z.; Ruan, L. M.; Li, B. X.(2016): Inverse geometry design of two-dimensional complex radiative enclosures using Krill Herd optimization algorithm.Applied Thermal Engineering, vol. 98, pp. 1104-1115.

Taler, J.; Duda, P.(2006):Solving direct and inverse heat conduction problems,Springer-Verlag, Berlin Heidelberg.

Tadeu, A.; Prata, J.; Simões, N.(2015): Dynamic simulation of three-dimensional heat conduction through cylindrical inclusions using a BEM model formulated in the frequency domain.Applied Mathematics and Computation, vol. 261, pp. 397-407.

Udayraj; Mulani, K.; Talukdar, P.; Das, A.; Alagirusamy, R.(2015): Performance analysis and feasibility study of ant colony optimization, particle swarm optimization and cuckoo search algorithms for inverse heat transfer problems.International Journal of Heat and Mass Transfer, vol. 89, pp. 359-378.

Valian, E.; Tavakoli, S.; Mohanna, S.; Haghi, A.(2013): Improved cuckoo search for reliability optimization problems.Computers & Industrial Engineering, vol. 64, pp. 459-468.Wu, C. H.; Jiang, R. Y.(2015): Three-dimensional free vibration analysis of sandwich FGM cylinders with combinations of simply-supported and clamped edges and using the multiple time scale and meshless methods.Computers, Materials & Continua, vol. 46, pp. 17-56.

Wang, S. H.; Lin, S. C.; Yang, Y. C.(2015): Geometry estimation for the inner surface in a furnace wall made of functionally graded materials.International Communications in Heat and Mass Transfer, vol. 67, pp. 1-7.

Yang, X. S.; Deb, S.(2009): Cuckoo search via Lé vy flights.NaBIC 2009, World Congress on IEEE, Coimbatore, December 9-11, pp. 210-214.

Yang, X. S.; Deb, S.(2010): Engineering optimisation by cuckoo search.International Journal of Mathematical Modelling and Numerical Optimisation, vol. 1, pp. 330-343.

Yu, B.; Zhou, H.L.; Chen, H. L.; Tong, Y.(2015): Precise time-domain expanding dual reciprocity boundary element method for solving transient heat conduction problems.International Journal of Heat and Mass Transfer, vol. 91, pp. 110-118.

Zhang, X. M.; Yu, J. G.; Zhang, M.; Zhang, D. P.(2015): Guided waves in functionally graded rods with rectangular cross-section under initial stress.Computers, Materials &Continua, vol. 48, pp. 163-179.