Generalized Rayleigh Wave Dispersion in a Covered Half-space Made of Viscoelastic Materials
2018-01-23AkbarovandNegin
S.D. Akbarov and M. Negin
1 Introduction
Surface waves propagating in viscoelastic layered media are of a particular importance for numerous scientific and engineering applications, from material science to biological science and from vibration reduction of different structural or mechanical elements to earthquake engineering and geophysical explorations. Several mathematical models have been used by many authors to study the dispersion and the attenuation behaviour of guided waves in such viscoelastic media. However, in most cases either they have described the viscoelasticity of the materials through some simple models such as the classical Kelvin-Voigt spring-dashpot models [see for instance, Chiriţă, Ciarletta and Tibullo (2014),Quintanilla, Fan and Lowe et al. (2015), Mazzotti, Marzani and Bartoli et al. (2012),Manconi and Sorokin (2013)] or they have used complex elasticity modulus instead of the real one in the stress–strain relations of the viscoelastic materials [see for instance,Vishwakarma and Gupta (2012), Barshinger and Rose (2004), Addy and Chakraborty(2005), Garg (2007), Jiangong (2011)]. Consequently, in general, such a simple viscoelastic models and the numerical results obtained within these models cannot illustrate the real character of the influence of the rheological parameters of the viscoelastic materials on the corresponding wave dispersion and attenuation. Recent efforts to use more realistic models for the wave propagation and attenuation problems in viscoelastic media were made by Meral, Royston and Magin (2009, 2011) by utilizing fractional order Voigt model to investigate Lamb wave propagation. In this way, a new rheological parameter which is the order of the fractional derivatives is introduced into the model and through this parameter the results are agreed more accurately with experiments as compared with conventional models.
Here we review in detail investigations related to the propagation of the Rayleigh waves in viscoelastic media which is close to the topic of the current paper and begin this review with the paper by Carcione (1992) in which the inelastic characteristics of the Rayleigh waves from the standpoint of balance energy is investigated. He calculated the quality factors as a function of the frequency and depth and showed that the viscoelastic properties calculated from energy considerations are consistent with those obtained from the Rayleigh secular equation. Based on the Cauchy residue theorem of complex analysis Lai and Rix (2002) presented a technique which permits simultaneous determination of the Rayleigh dispersion and attenuation curves for linear viscoelastic media with arbitrary values of material damping ratio. Fan (2004) obtained the analytical solution of the Rayleigh wave propagation phenomena considering the nonlinear damping mechanism of seismic waves by applying the perturbation method. Pasternak (2008) analysed the Rayleigh wave propagation problem in the elastic half-space and viscoelastic layer interface using in the Fourier-Laplace space using the Biot viscoelastic solid model.Sharma, Sharma and Sharma (2009) derived the complex secular equations for Rayleigh wave propagation in closed and isolated mathematical conditions and studied the thermoselastic interaction in an infinite Kelvin-Voigt type viscoelastic, thermally conducting solid bordered with viscous liquid half-spaces/layers of varying temperature. Zhang, Luo and Xia et al. (2011) studied the dispersion of Rayleigh waves in viscoelastic media by applying pseudo spectral modelling method to obtain high accuracy for Rayleigh wave modelling in viscoelastic media. In pseudo spectral method the spatial derivatives in the vertical and horizontal directions are calculated using Chebyshev and Fourier difference operators, respectively. Chiriţă, Ciarletta and Tibullo (2014) studied the propagation of surface waves over an exponentially graded half-space of isotropic Kelvin-Voigt viscoelastic material by means of wave solutions with spatial and temporal finite energy.They showed that when there is just one wave solution it is found to be retrograde at the free surface, while when there is more than one viscoelastic surface wave, one is retrograde and the others are direct at the free surface.
We also note investigations carried out in the papers by Sharma (2005), Sharma and Othman (2007), Kumar and Parter (2009), Sharma and Kumar (2009), Abd-Alla, Aftab Khan and Abo-Dahab (2017) and others listed therein in which the Rayleigh-Lamb waves dispersion in the plate made of viscoelastic or thermo-viscoelastic materials are investigated. However, it should be noted that in these works the viscoelasticity of the plate material is described by the Voigt model. Moreover, it should be noted that the investigations carried out in these works are also have important significance in the methodological sense, i.e. in these works the functional iteration numerical technique is developed for determination of the complex roots of the secular equation. Detailed consideration of this method and its advantage and disadvantages are discussed in the paper by Sharma (2011). We will again turn below to this method in the text of the paper during the discussions the solution algorithm of the secular equation.
As follows from the foregoing discussion and works reviewed above, the investigations on the dispersion of the guided waves in the half-space or covering half-spaces made from viscoelastic materials mainly were carried out by employing simple Kelvin-Voigt classical models or by using frequency dependent complex modulus of viscoelastic materials which is obtain from the experiments. These simple methods were not actually connected with the more complicated and real behaviour of viscoelastic materials and they do not illustrate the influence of the rheological parameters of the viscoelastic materials on this dispersion.These considerations led the authors to study the generalized Rayleigh waves dispersion and attenuation for a system consisting of a viscoelastic covering layer and a viscoelastic half-space utilizing more realistic mathematical viscoelastic model using Rabotnov (1980)fractional exponential operator which are already used in the papers by Akbarov and Kepceler (2015), Akbarov, Kocal and Kepceler (2016a, 2016b) and Kocal and Akbarov(2017) under investigations of the axisymmetric torsional and longitudinal waves respectively in the layered hollow cylinders made of viscoelastic materials. Moreover, in the paper by Akbarov (2014) this model is employed to study of the axisymmetric timeharmonic Lamb’s problem for a system consisting of s viscoelastic covering layer and viscoelastic half-space. Note that these results in these papers are also detailed in the monograph by Akbarov (2015).
Moreover, this study, actually extends the authors previous works Negin, Akbarov and Erguven (2014), Negin (2015) and Akbarov and Negin (2017) on propagation of the generalized Rayleigh waves in an initially stressed elastic covered half-space to viscoelastic cases, where the constitutive relations for the covering layer and the half-space materials are described through the fractional exponential operator by Rabotnov (1980).The investigations are carried out within the framework of the piecewise homogeneous body model by utilizing exact equations of motion of the linear theory of viscoelasticity and it is assumed that perfect contact conditions take place on the interface surface between the layer and the half-space. The theoretical results obtained in this paper can be utilized in many relevant practical problems of wave propagation in viscoelastic layered media which play roles in areas like engineering, earthquake and geophysical sciences etc. Some numerical calculations, discussions and conclusions will be discussed in their proper places.
2 Formulation of the problem
The system consists of a layer with thicknesswhich covers a half-space as shown in Fig.1. The layer and the half-space occupy the regionsrespectively. We assume that the materials of the constituents are isotropic, homogeneous and hereditaryviscoelastic. Positions of the points are determined in the Cartesian system of coordinatesplane is considered.
Below the values related to the layer and half-space are denoted by upper indices (1) and(2), respectively.
The governing equations of motion and mechanical relations for the case under consideration are as follows:
The equations of motion:

Constitutive and geometrical relations:
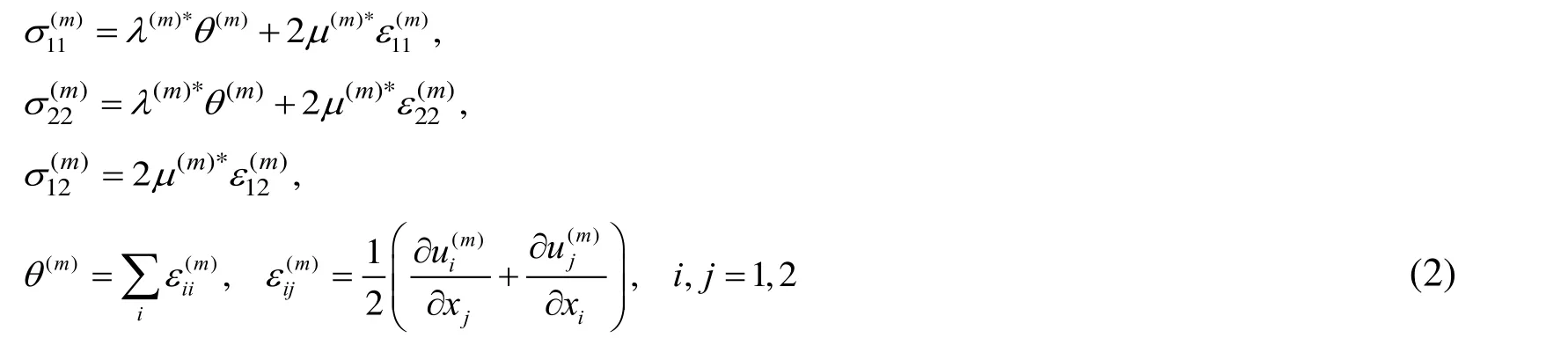
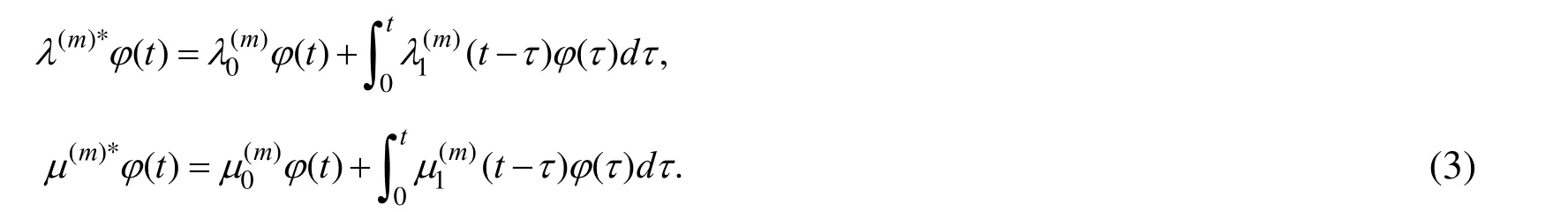
We assume that the following boundary conditions on the free face plane and contact conditions on the interface of the covering layer and half-space satisfy:
Boundary conditions:

Contact conditions:

We also assume that the following decay conditions are satisfied:


Figure 1: Geometry of the covered half-space.
This completes the formulation of the problem under consideration the novelty of which is the mathematical modelling of the near-surface (or generalized Rayleigh) wave propagation in the system consisting of the covering layer and half-space made of viscoelastic materials with arbitrary hereditary properties.
3 Method of Solution
According to the problem nature we can represent the sought values in the following form:

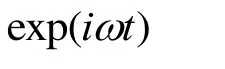
Thus, after the foregoing discussions we turn to consideration of the solution method and using the relation

in (2) and (3) and taking equations (7) and (8) into account we can write the following relation:
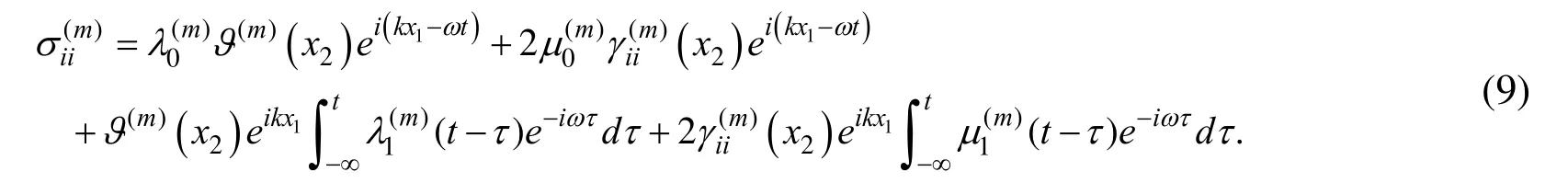
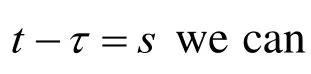
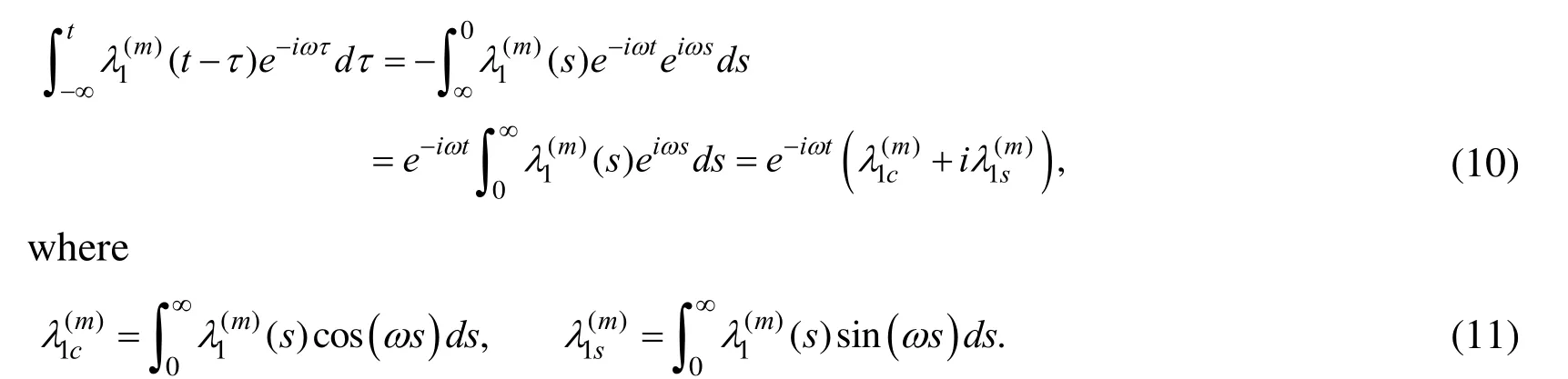
In a similar manner, we obtain
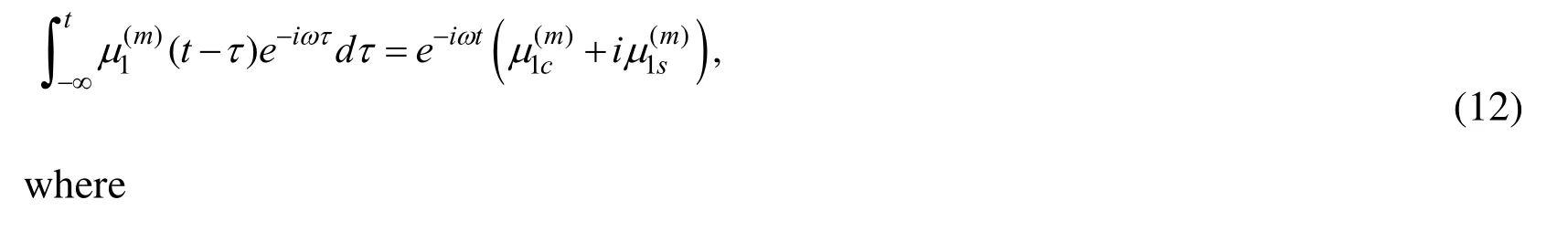
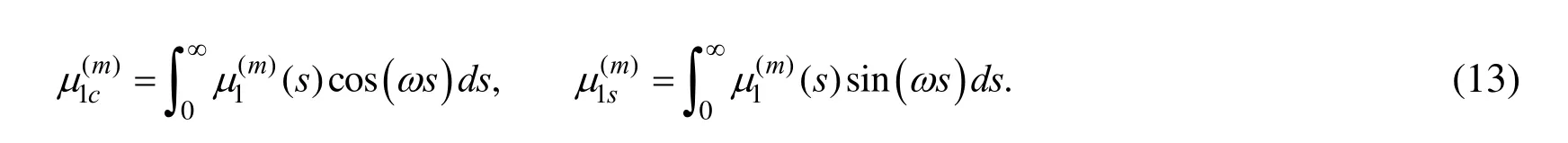
Taking the relations (10)-(13) into account we can write the following expressions for the stresses:
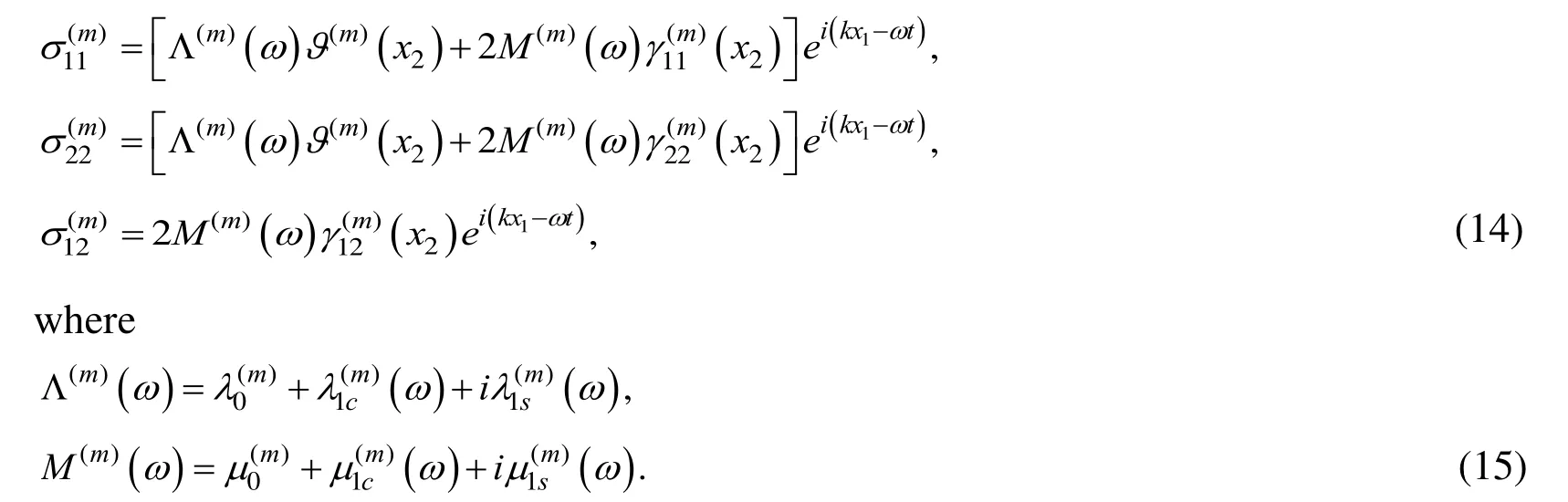
Thus, we obtain the complex modulus,instead of Lame constants in the relations (2) and (3), the real and imaginary parts of which are determined through the expressions (11), (13) and (15). This means that the complete system of field equations(1), (2), (11), (12) and (15) for the viscoelastic system, can also be obtained from those written for the purely elastic system by replacing the elastic Lame constantswith the complex constantsforegoing mathematical calculations confirm the dynamic correspondence principle (see Fung (1965)) for the problem under consideration and the solution method used here agrees with this principle.
Thus, according to the foregoing procedures, the system of equations (1), (2) and (3) with boundary conditions (4) and (6), and contact condition (5), can be solved analytically by employing the so-called method of separation of variables. Also, it follows from the foregoing procedures that the presentation of the sought values through the variables andtis made through the known functionsand, respectively.However, the presentation of the sought values through the variableis made through the unknown functions(7) and (14) into the equation of motion (1) we obtain the following equations for these unknown functions:

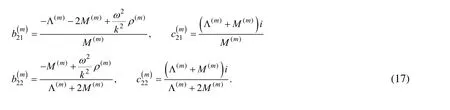
It can be written from the second equation in (16) the following expressions
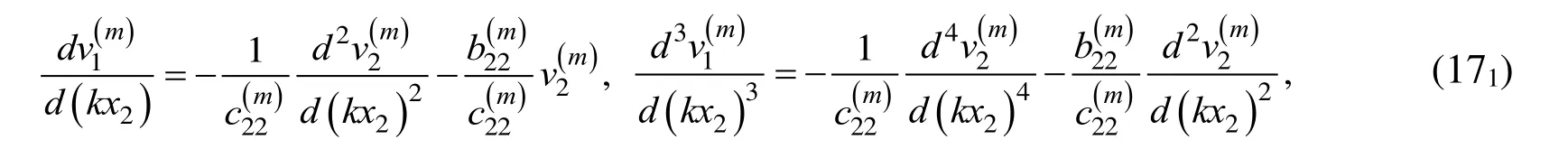
and it can be written the following expression from the first equation in (16)

Thus, substituting the expressions in (171) into the expression (172) we obtain:

The general solution of the equation (18) for them-th layer can be written as follows:


Finally, substituting the expressions in (20) into the equations (7) and (2) and employing well-known usual procedure we obtain the following dispersion equation from the boundary (4) and contact (5) conditions (4)-(6):


Thus, in the present section the analytical expression for the dispersion equation related to the near-surface (or generalized Rayleigh) wave propagation in the system consisting of the covering layer and half-space made of viscoelastic materials with arbitrary hereditary properties are obtained.
4 Numerical results and discussions
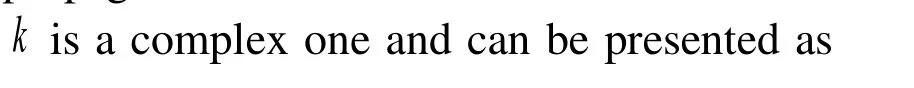

We determine the phase velocity of the studied waves through the expression:

We assume that the viscoelasticity of the materials of the constituents is described through the fractional exponential operator by Rabotnov (1980), i.e. we assume that
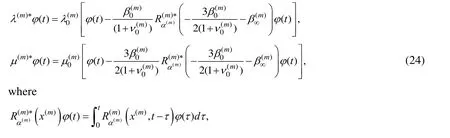
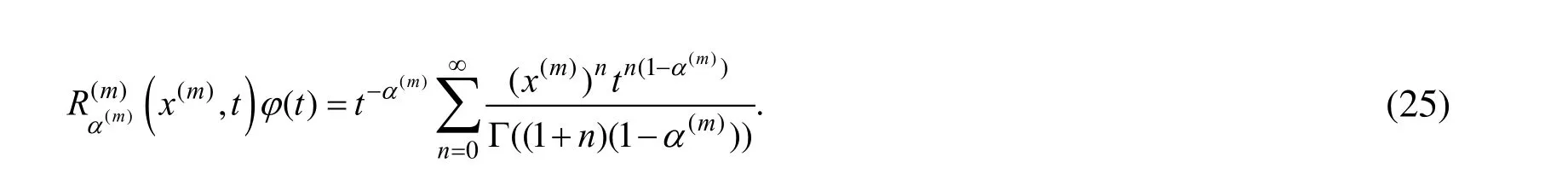
Introducing the following dimensionless rheological parameters,



The dimensionless rheological parameterin (26) characterizes the long-term values of the viscoelastic materials and the rheological parametercharacterizes the creep time of the viscoelastic materials, and finally the rheological parametercharacterizes the form of the creep (or relaxation) function for them-th material and the case wherecorresponds to the ‘standard viscoelastic body’ model (or the model by Kelvin).With respect to solution of the dispersion equation (21), as the values of the determinant obtained in (21) are complex, the dispersion equation can be reduced to the following one

According to the physico-mechanical consideration, in finding the velocitywhich is the root of the equation (31) for the selectedgreater (less) than that obtained in the corresponding purely elastic case with the elastic constants calculated at(at). This ensures the existence of the roots of the equation (31).
Thus, we consider the numerical results obtained from the solution of the dispersion equation (31) by employing the algorithm discussed above. First, we analyse the case where the attenuation of the materials is low and according to Ewing, Jazdetzky and Press(1957) and Kolsky (1963) we assume that
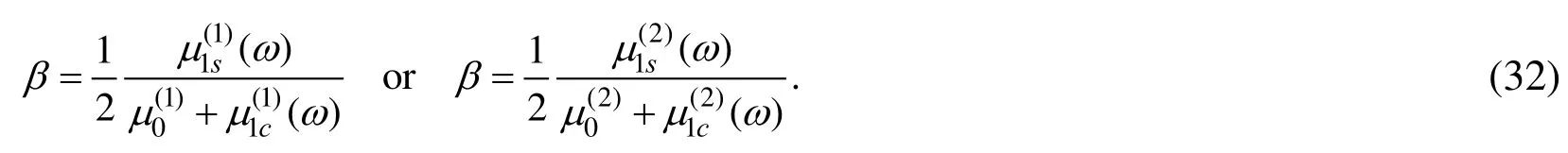
It should be noted that the attenuation determined by the relation (32) relates to the dispersive attenuation case. At the same time, the non-dispersive attenuation case underwhich the selected values for (or) in (22) do not depend on the wave frequencyalso is considered in the present investigations.
Note that the solution technique of the secular equation described above has also been used in the paper by Barshinger and Rose (2004). In general, as noted in the paper by Sharma(2011), there is no general method for finding the complex roots of the transcendental secular equations. Theoretically, it is known that the functional iteration method detailed by Sharma (2011) can be applied for determination of the complex roots of an analytical function. In this method the analytical function is represented in the finite power series form and the obtained algebraic equation is solved through the iteration method. Namely this method is developed for solving the secular equations with complex roots and employed in the papers Sharma (2005), Sharma and Othman (2007), Kumar and Parter(2009), Sharma and Kumar (2009) and others listed therein. For instance, in the paper Sharma (2005) the Rayleigh-Lamb wave’s dispersion in the viscoelastic plate is studied and the corresponding secular equation is solved by the use of the aforementioned functional iteration method. The key step in the application of this method is the successful selection of the initial guess. However, we have not found in the papers Sharma (2005)and Sharma and Othman (2007) what initial guess is taken under employing the iteration procedure. Nevertheless, it can be predicted that the sought complex root must be near to the certain complex root of the secular equation obtained in a special limit cases in which it is possible to obtain an analytical expression for the complex root. Note that such limit cases and determination of the exact complex roots in these cases take place in the investigations carried out in Sharma (2005), Sharma and Othman (2007), Kumar and Parter (2009) and Sharma and Kumar (2009). We think that namely this and similar type complex roots can be taken as initial guess for employing the functional iteration method.In the cases where there is no the aforementioned situation, the selection of the initial guess for the complex root is difficult and there is no any rule for selection the mentioned initial guesses. This statement is the disadvantage of the functional iteration method. At the same time, this method allows to find the real and imaginary parts of the complex roots simultaneously. This is the advantage of the functional iteration method. However, the solution method described above and applied in the present and earlier works Akbarov and Kepceler (2015), Akbarov, Kocal and Kepceler (2016) the values of the attenuation coefficient are given a priori for finding the wave propagation velocity, or as in the paper Barshinger and Rose (2004) the values of the wave propagation velocity are selected a priori for finding the attenuation coefficient. Of course, this is disadvantages of the used method. However, this method does not require the selection of any initial guesses which is advantage of method.
Note that, as noted above, in the case under consideration we prefer to use the solution algorithm described above and used also in the papers Barshinger and Rose (2004),Akbarov and Kepceler (2015) and Akbarov, Kocal and Kepceler (2016), Kocal and Akbarov 2017). This is because, employing the functional iteration method for the solution of the secular equation obtained in the present paper requires special consideration and development of this method which has not been done up to now.
Thus, we turn to the analysis of numerical results which are obtained for such cases where the conditionsandare satisfied simultaneously where theare determined through the expression in (20) andis a complex wavenumber presented as in (22). Namely, satisfaction of these conditions provides the existence of the near-surface (or generalized Rayleigh) waves in the bi-material viscoelastic system under consideration. According to the mentioned conditions,numerical investigations are made within the scope of the assumptionsfor which it can be provided the satisfaction of the conditionsandthroughout all the calculation procedures.



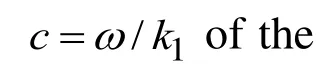
Note that the foregoing conformations of the obtained numerical with the related predictions and agreement of those with the known physico-mechanical considerations can be taken as validation and trustiness of the used calculation algorithm and PC programs which are composed by the authors and are realized in MATLAB. Unfortunately,we have not found any related numerical results in literature in order to compare these results with those.
We turn again to the consideration of the limit values of the wave propagation velocity as. Thus, in general, according to the foregoing discussions, and conclusions we can write the following relation

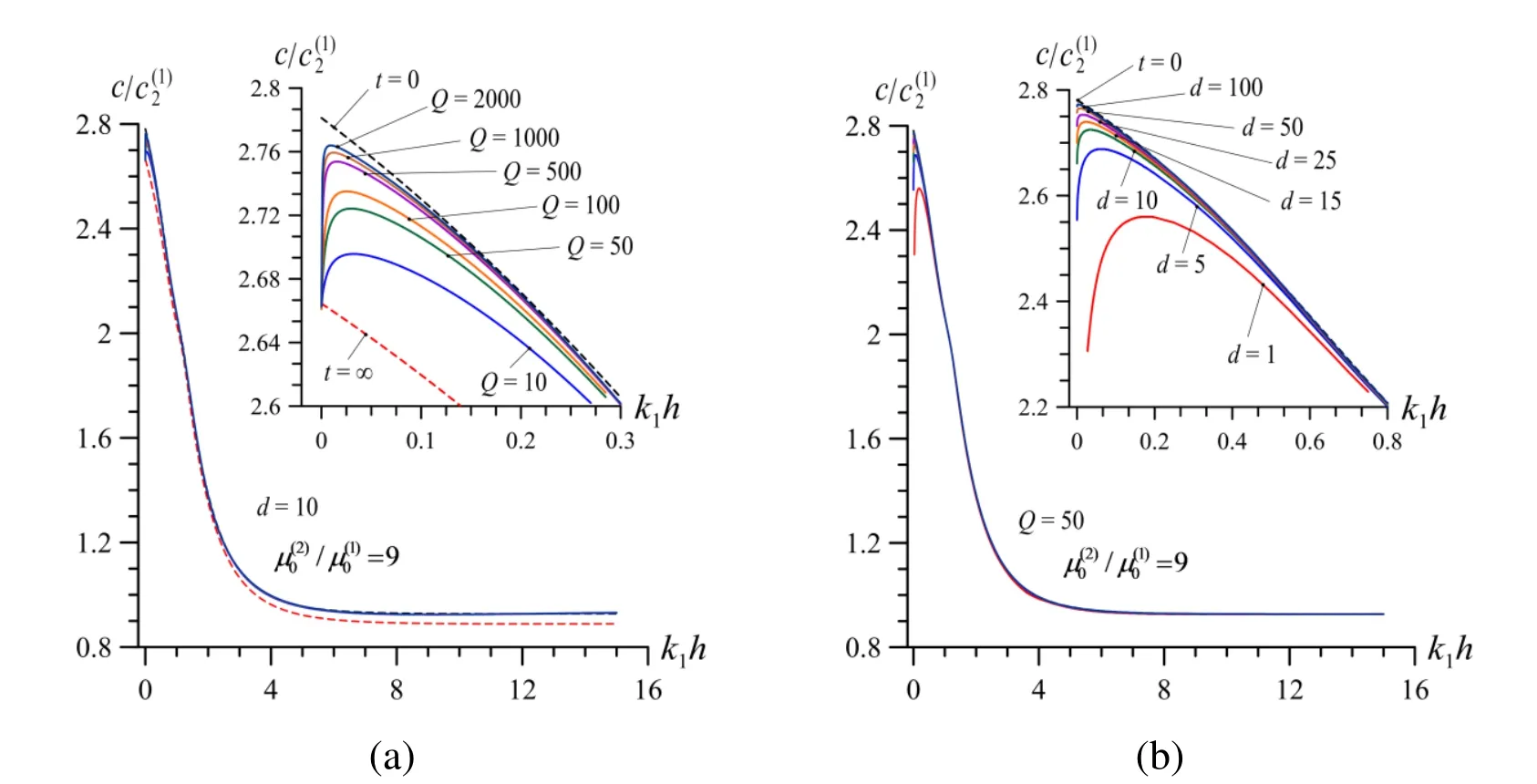
Figure 3: Dispersion curves in V.V. case ned for (a) various values of the parameter under a fixed value of the parameter (b) for various values of the parameter under a fixed value of the parameter .

The wave propagation velocity and dimensionless wavenumber related to this case we denote byandrespectively. Note that for the dispersion curves related to the purely elastic waves there is not the case where the relation (35) takes place. Consequently,the appearing of the cases where the relation (35) takes place is caused namely with the viscoelasticity of the materials of the constituents of the system under consideration.
We analyse the physico-mechanical meaning of the relation (35). In the wave propagation sense the relation (35) means that in the case where this relation satisfies the phase velocity of the wave propagation becomes equal to the corresponding group velocity. According to this statement, in the cases where (in the cases wherethe dispersion of the waves for viscoelastic case is anomalous (normal) dispersion. At the same time, the relation (35) means that the velocity is root of the second order of the dispersion equation (21) (or (31)). According to the numerous investigations on the dynamics of the moving load acting on the ‘covering layer + half-space’ systems, for instance in the monograph by Akbarov (2015) and many others listed therein, the velocity which is second order root of the dispersion equation, i.e. under which the relation (35)takes place, is the critical velocity of the corresponding moving load. We recall that under this velocity of the moving load the resonance type accidents appear.

?
Table 2: The values of the obtained in the case indicated in Fig.2b under
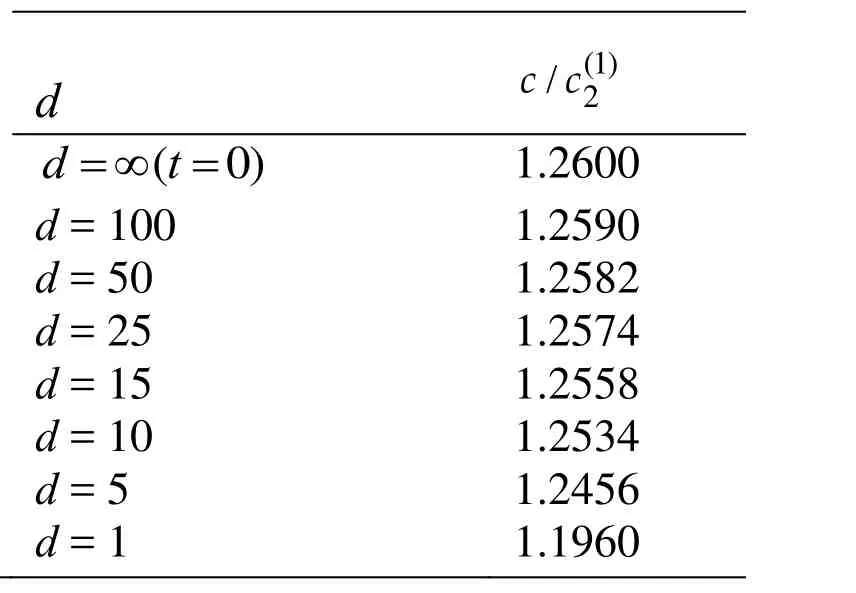
Table 2: The values of the obtained in the case indicated in Fig.2b under
d .2600.2590.2582.2574.2558.2534.2456.1960
Thus, it follows from the foregoing discussions that, the viscoelasticity of the materials of the constituents influences on the dispersion curves of the generalized Rayleigh waves not only in the quantitative sense but also in the qualitative sense. Moreover, it follows from the foregoing results that under investigations of the dynamics of the moving load acting on the systems which can be modelled as the ‘covering layer + half-space’ the appearing of the critical velocities as a result of viscoelasticity of materials of the constituents must be taken into consideration.
For a clear illustration of the amount of the influence of the materials' viscosity on the wave propagation velocity in the cases considered in Figs. 2 and3, the values of these velocity are presented in Tables 1, 2, 3 and 4 in the cases where (Tables 1 and 2) and(Tables 3 and 4). It follows from these data that in the quantitative sense the influence of the rheological parameteronthe wave propagation velocity is moresignificant than that of the rheological parameter .
Table 3: The values of the obtained in the case indicated in Fig.3a under
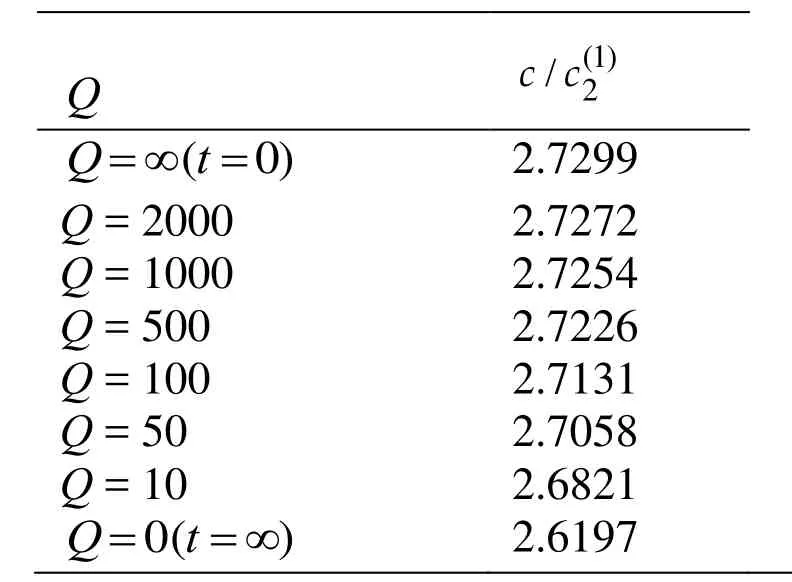
Table 3: The values of the obtained in the case indicated in Fig.3a under
?
Table 4: The values of the obtained in the case indicated in Fig.3b under
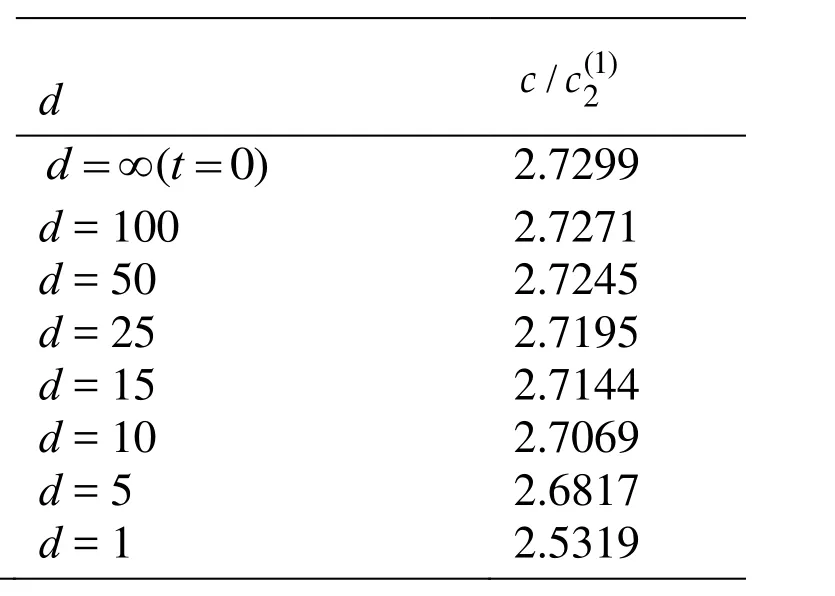
Table 4: The values of the obtained in the case indicated in Fig.3b under
d 2.7299 2.7271 2.7245 2.7195 2.7144 2.7069 2.6817 2.5319


Consider graphs of the dependence of the attenuation coefficientand dimensionlesswhich are given in Fig. 4 for various values of the rheological parameterdunder a fixed(Fig. 4a) and for various values of the rheological parameterunder a fixed(Fig. 4b) when. Using these results and the results obtained for the dispersion curves, for instance, for the dispersion curves given in Figs. 2 and 3, one can easily determine the value of the attenuation coefficient for each selected value of the wave propagation velocity. Note that this statement remains valid also for all the results which will be considered below.
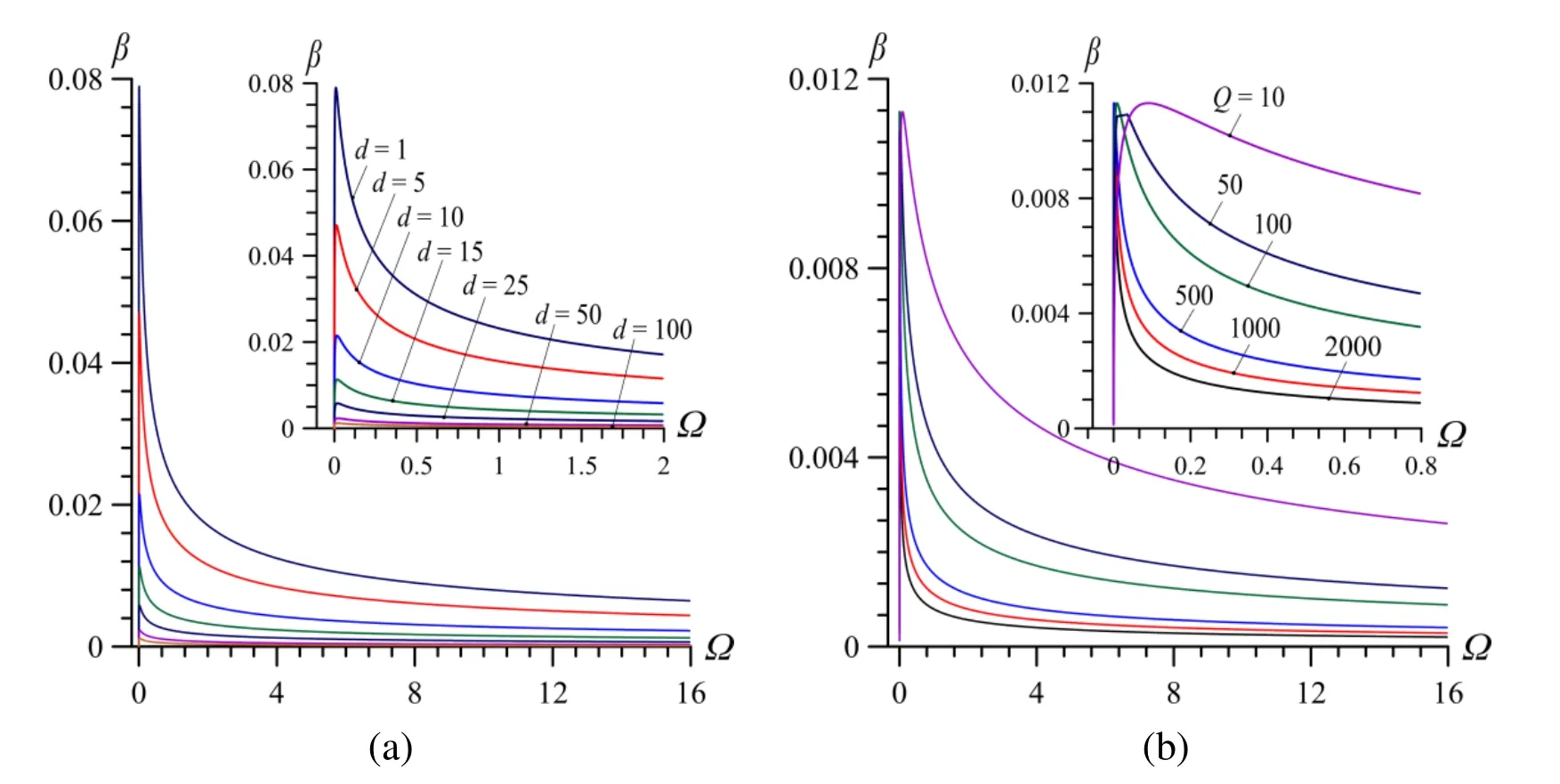
Figure 4: (a) The influence of parameter )on under and (b) the influence of parameter on under .
Now we attempt to answer a question what contribution is made the viscoelasticity of each constituent of the system under consideration on the dispersion curves and for this purpose we consider the graphs given in Figs. 5-8 which are obtained in the case whereNote that in these figures the graphs grouped by lettera(letterb) relate to the case where the rheological parameters related to the half-space (to the covering layer)material are changed and the rheological parameters related to the covering layer (to the half-space) are fixed. Moreover, note that the results given in Figs. 5 and 7 (Figs. 6 and 8)relate to the case wheree case whereresults given in Figs. 5 and 6 (in Figs. 7 and 8) illustrate the influence of the rheological parametersand(rheological parametersand) on the dispersion curves. Thus, it follows from the graphs given in Figs. 5-8 that the main contribution on the dispersion curves is made by the viscoelasticity of the half-space material.

Figure 5: Dispersion curves in V.V. case or different values of parameter when and (b) for different values of parameter when and .
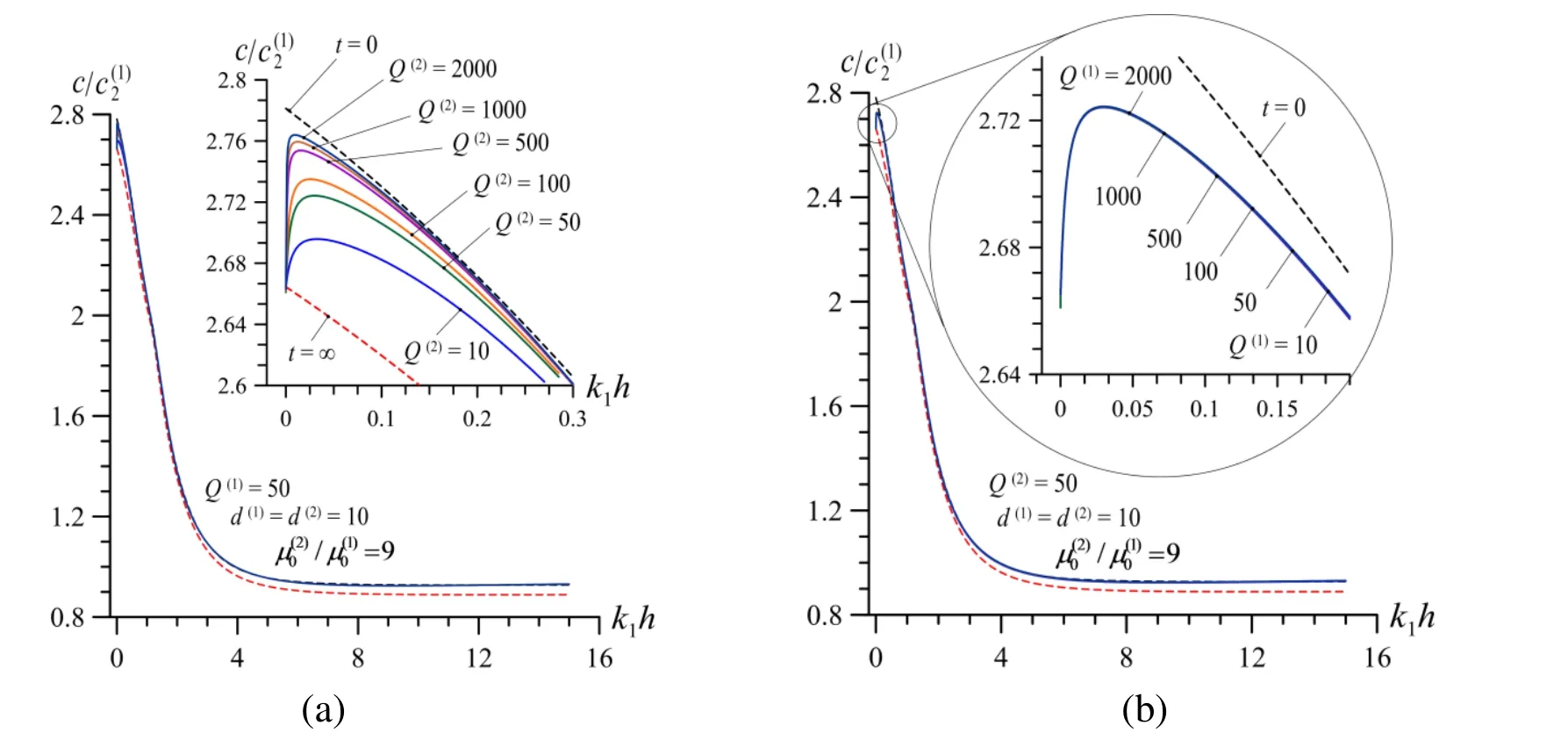
Figure 6: Dispersion curves in V.V. case or different values of parameter when and (b) for different values of parameter when and .
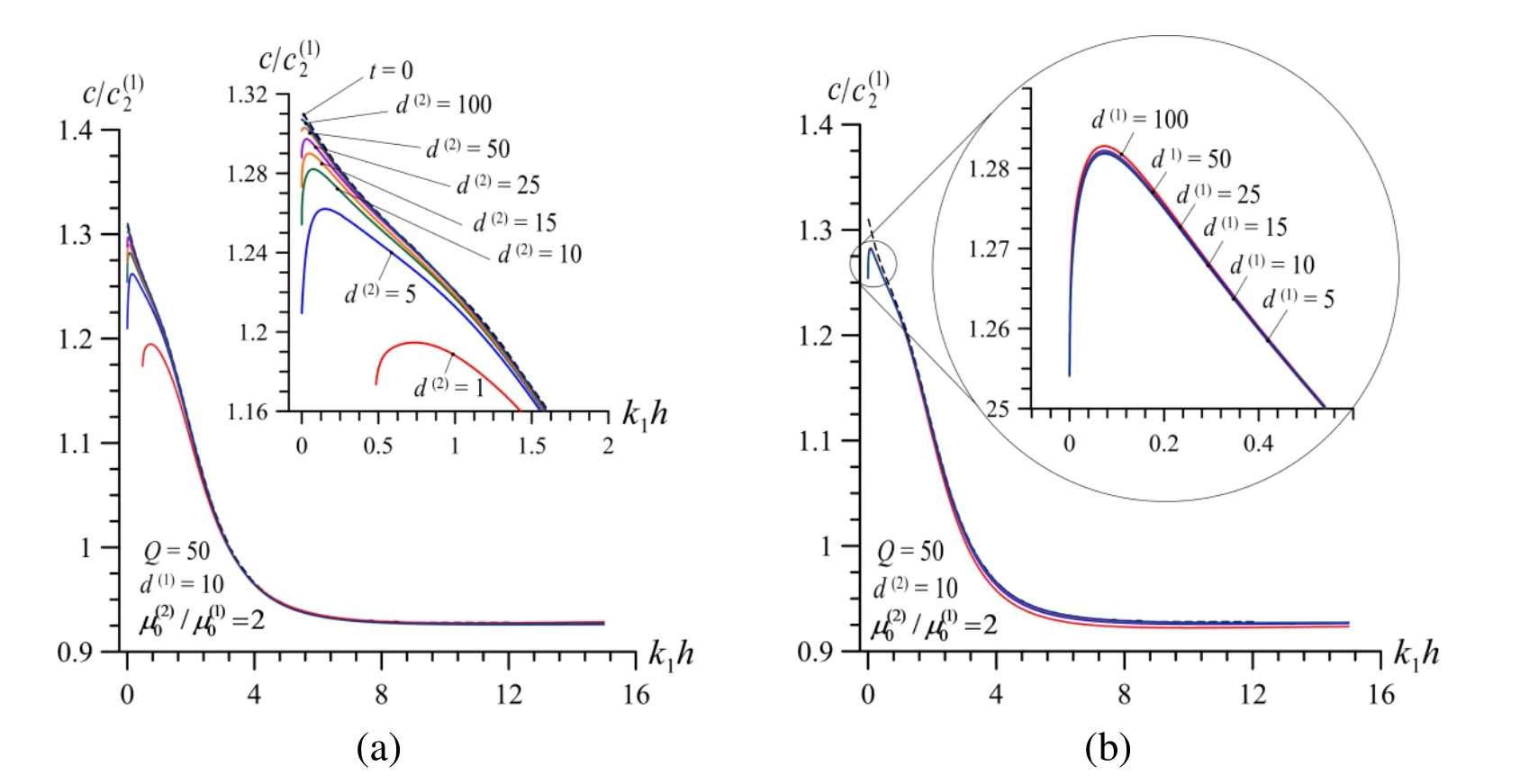
Figure 7: Dispersion curves in V.V. case or different values of parameter when and (b) for different values of parameter when and .

Figure 8: Dispersion curves in V.V. case or different values of parameter when and (b) for different values of parameter when and .
We recall that the foregoing results are obtained in the cases where both the materials of the covering layer and the half-space are viscoelastic, i.e. the V.V. case. Now we consider the results obtained in the case where the material of the covering layer is purely elastic,but the material of the half-space is viscoelastic and denote this case as the E.V. case. Note that the all foregoing results for this case are obtained within the scope of the attenuation determined by second expression in (32). Fig. 9 shows the graphs obtained for the case E.V. whenifferent values of parameter(Fig. 9a) under fixed values of parameterand for different values of parameter(Fig. 9b) under fixed values of parameter.
Comparison of the graphs given in Fig. 9a with the corresponding V.V. ones given in Fig.5a shows that the influence of the rheological parameters of the half-spaceon the dispersion curves obtained in the E.V. case underost the same as in the V.V. case. However, comparison of the graphs given Fig. 9b with the corresponding V.V. ones given in Fig. 7a shows that the influence of the rheological parameters of the half-spaceon the dispersion curves obtained in the E.V. case is more significant than that obtained in the V.V. case. We do not consider here the numerical results obtained for
E.V. case because these results in the qualitative sense are the same.
Now we consider the results related to the effect of rheological parameterson the wave dispersion curves in the case wheredote that the influence of this rheological parameter on the wave dispersion is considered for the first time in the present paper and this effect has not been examined in the papers by Akbarov and Kepceler (2015) and in the paper by Akbarov, Kocal and Kepceler (2016).Thus, we consider graphs given in Figs. 10–13 which illustrate the mentioned influence.Note that these graphs are constructed in the cases where. 11 and 12)and. 12 and 13). Moreover, note that the graphs given in Figs. 10 and 12 (Figs. 11 and 13) show the effect of the rheological parameteron the dispersion curves under various values of the rheological parameter(of the rheological parameter) for a fixed value of the rheological parameter(for a fixed value of the rheological parameter). The graphs given in Figs. 10 and 12 (in Figs. 11 and 13)and grouped by lettersa,b,canddcorrespond the cases where, 50, 100 and 500(the case where, 10, 25 and 50) respectively.
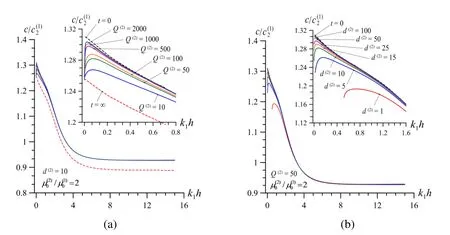
Figure 9: Dispersion curves in E.V. case or different values of parameter when (b) for different values of parameter when .
Thus, it follows from the results given in Figs. 10–13that in the all considered cases thereexists such value of the dimensionless wavenumber (denote it by at which the change in the values of the rheological parameterdoes not influence on the values of the wave propagation velocity. However, in the cases wherein the casesan increase in the values of the parametercauses a decrease (an increase) in the wave propagation velocities. According to the aforementioned numerical results, it can be concluded that thedepends on the values of the rheologicaland an increase in the values of these parameters causes to decrease of the. Moreover, it can be concluded the values of thedepends also on the ratiod an increase of this ratio causes a decrease in the values of the
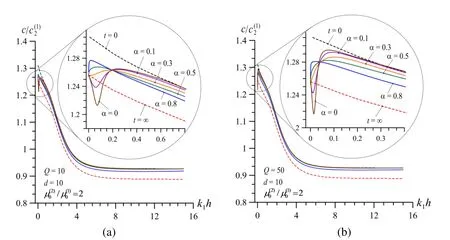
Figure 10: Dispersion curves in V.V. case for different values of parameter and when and
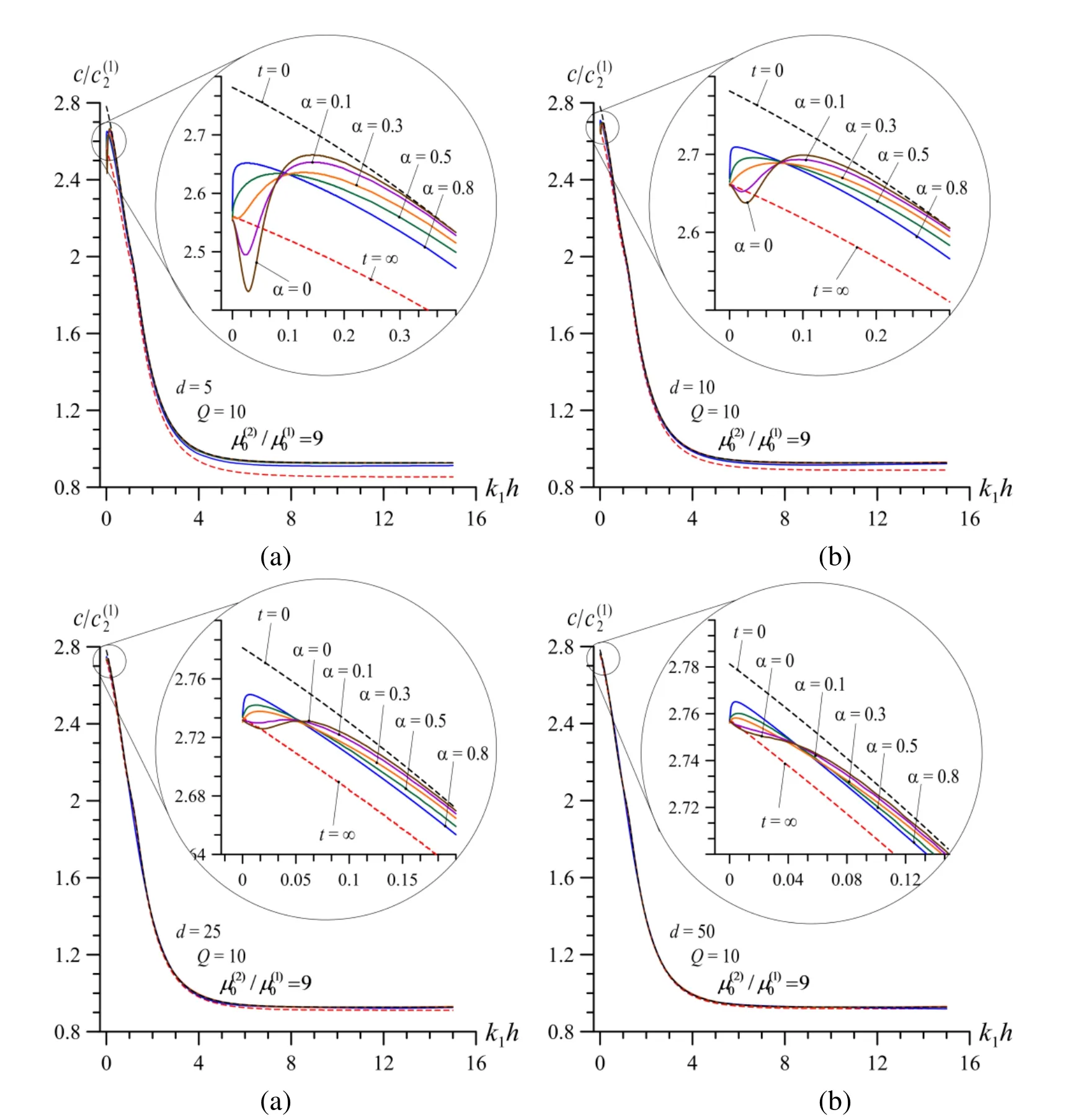
Figure 13: Dispersion curves in V.V. case for different values of parameter and when and
Note that besides of all these it can be concluded that the change in the values of the rheological parameterdoes not influence on the limit values of the wave propagation velocity as. However, in the near vicinity of this limit case, if to say more precisely in the regionhe influence of the rheological parameteron the dispersion curves is significant not only in the quantitative sense but also in the qualitative sense. So that under small values of the, for instance under, 0.1, the dispersion curves have well-defined minimum in the regionnd at this minimum the relation (35) takes place. Moreover, in the near vicinity of this minimum the wave propagation velocity obtained for the viscoelastic cases become less than that obtained for the purely elastic case with long-term values of elastic constants at. Consequently,in the region decrease in the values of thecauses to change the character of the dispersion curves. However, with increasing ofthe aforementioned minimum disappears in the dispersion curves and wave propagation velocities are limited with the wave propagation velocities obtained for the purely elastic cases with instantaneous values of elastic constants atof elastic constants at(lower limit).
Thus, the all foregoing results and discussions allow us to conclude that in investigations of the wave propagation in elements of constructions made of viscoelastic material the viscoelastic relations of which are described through the fractional exponential operators it is necessary to take into consideration the influence of the rheological parameteron this propagation.We recall that all the foregoing results are obtained for the dispersion attenuation case with the attenuation coefficientdetermined through the expression (32), according to whichas. This statement can be proven as follows:According to the expressions in (30) we can see thatandas.This is becausein the first expression in (30). Taking this limit value of the parameterinto account we obtain from the expressions given in (29) thatandas. According to these limit values, it follows from the expressions in (28) thatand also, it follows from the expressions in (32) (or from the expressions in (36)) thatas.
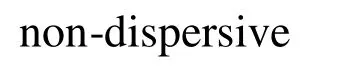
Thus, analyse the graphs given in Fig. 14 which illustrate the dispersion curves obtained for the non-dispersive attenuation case under,ndr the case wherethat these graphs are constructed for the various values of the parameterunder fixed value of the(Fig. 14a) and for the various values of the parameterunder fixed(Fig. 14b). It follows from these results that as a result of the non-dispersity of the attenuation of the waves propagated in the viscoelastic materials the ‘cut off’ values of the wavenumberappear. We denote this ‘cut off’ value throughand note that if we multiplywith the corresponding wave propagation velocitythen we obtain the corresponding ‘cut off’frequency.
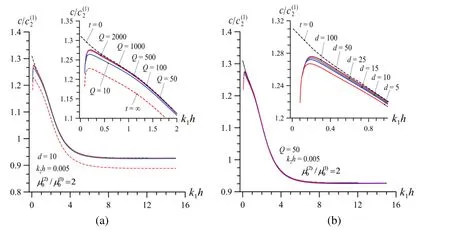
Figure 14: Dispersion curves obtained in the non-dispersive attenuation case underin the V.V. case (a) for various values of the parameter under a fixed value of the parameter d (b) for various values of the parameter under a fixed value of the parameter the V.V. case under

Figure 15: The influence of the ‘attenuation order’ on the cut off values of , i.e.on the values of in the case considered in Fig. 14.
It follows from Fig. 14 that the change in the rheological parameterdoes not influence on the values of the, however an increase in the values of the rheological parametercauses to increase the values of theFig. 15 shows the dispersion curves constructed for various values of the “attenuation order”in the case whereandfrom which follows that the values of theincrease monotonically with the
Thus, the results given in Figs. 14 and 15 allow us to conclude that as a result of the dispersity of the attenuation of the waves under consideration the ‘cut off’ wavenumbers or frequencies disappear.
The experimental evaluation application of the numerical results obtained in the present paper can be made in the following manner. First, it is necessary to model the viscoelasticity of the materials of the constituents of the system through the fractional exponential operators by Rabotnov and to determine the values of the corresponding rheological parameters which enter to these operators. After it can be used the traditional methods on the measurement of the near surface wave propagation velocities for determination of the influence of the rheological parameters of the materials to this velocity. The obtained numerical results allows to use those not only in the aforementioned for measurements procedures in the concrete selected cases but also these results allows to have theoretical knowledge on the character of this influence in the principal sense.This completes the discussions of the numerical results.
5 Conclusions
Thus, in the present paper dispersion of the generalized Rayleigh waves in the ‘covering layer + half-space’ system made of viscoelastic materials is investigated. The investigations carried out within the scope of the piecewise homogeneous body model by utilizing the exact equations of motion of the theory of linear viscoelasticity in the plane strain state.
The main processing flow of investigations carried out in the present paper is as follows:1) the analytical expressions of the sought values are determined for arbitrary kernel functions in the operators described the viscoelasticity of the materials by employing the method of separation of variables;
2) the corresponding dispersion equation is also obtained for arbitrary hereditary type viscoelastic operators;
4) numerical investigations are made for the cases where the wave attenuation coefficients are determined through the expressions in (32);
5) These results are obtained for the cases under which the generalized Rayleigh waves exists, i.e. under which the conditionsandsatisfy simultaneously, where theandare determined through the expression in (20) andis a complex wavenumber determined as in (22);and finally
6) The numerical results are presented and discussed mainly for the attenuation dispersion case and at the same time a few numerical examples are also presented and discussed for the non-dispersive attenuation case.
Moreover, these results are obtained for the case where the viscoelasticity properties of the covering layer and the half-space materials are the same (denoted as V.V. case) and for the case where the material of the covering layer is purely elastic, but the material of the half-space is viscoelastic (denoted as E.V. case). According to these numerical results,the following main conclusions can be drawn:
• In both V.V. and E.V. cases in the considered attenuation dispersion case the viscoelasticity of the materials causes the generalized Rayleigh wave propagation velocity to decrease. The magnitude of this decrease increases with a decrease in the aforementioned dimensionless rheological parameters and;
• The character of the influence of the parameteron the wave velocities and on the dispersion corves depends on the values of the dimensionless wave numberand on the values of the rheological parametersand. There exist such value of theafter (before) which an increase in the values of thecauses to decrease (to increase) the wave propagation velocity;
• The satisfaction of the relation (35) conforms the appearing of the critical velocities of the moving load acting on the system under consideration as a result of the viscoelasticity of the materials of the constituents of the system;
• In general, the dispersion curves obtained to viscoelastic cases are limited by the dispersion curves corresponding to the purely elastic case with instantaneous values of the elastic constants (upper limit) and by those obtained for the purely elastic case with long-term values of the elastic constants (lower limit), however this rule is violated in the relatively small values of the rheological parameterunder which the wave propagation velocity can become less than the mentioned lower limit;
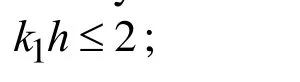
• For all the considered cases, the high wavenumber limit values of the wave propagation velocity does not depend on the rheological parameters of the materials;
• The main influence on the dispersion curves is caused by the viscoelasticity of the half-space material and the influence of the viscoelasticity of the covering layer material on these curves is insignificant;
• In the nondispersive attenuation case, the cut off values of the arise and these values increase with the non-dispersive ‘attenuation order’
Abd-Alla, A. M.; Aftab Khan; Abo-Dahab, S. M.(2017): Rotational effect on thermoelastic Stoneley, Love and Rayleigh waves in fibre-reinforced anisotropic general viscoelastic media of higher order.CMC: Computers, Materials & Continua,vol. 53, no.1, pp. 52-72.
Addy, S.K.;Chakraborty, N. R.(2005): Rayleigh waves in a viscoelastic half-space under initial hydrostatic stress in presence of the temperature field.International Journal of Mathematics and Mathematical Sciences,vol. 24, pp. 3883-3894.
Akbarov, S. D.(2014): Axisymmetric time-harmonic Lamb’s problem for a system comprising a viscoelastic layer covering a viscoelastic half-space.Mechanics of Time-Dependent Materials,vol. 18, no. 1, pp. 153-178.
Akbarov, S. D.(2015):Dynamics of pre-strained bi-material elastic systems: Linearized Three-Dimensional Approach. Springer.
Akbarov, S. D.; Kepceler, T.(2015): On the torsional wave dispersion in a hollow sandwich circular cylinder made from viscoelastic materials.Applied Mathematical Modelling, vol. 39, no. 13, pp. 3569-3587.
Akbarov, S. D.; Kocal, T.; Kepceler, T.(2016a): Dispersion of axisymmetric longitudinal waves in a bi-material compound solid cylinder made of viscoelastic Materials.CMC: Computers, Materials & Continua,vol. 51, no. 2, pp. 105-143.
Akbarov, S. D.; Kocal, T.; Kepceler, T.(2016b): On the dispersion of the axisymmetric longitudinal wave propagating in a bi-layered hollow cylinder made of viscoelastic materials.International Journal of Solids and Structures, vol. 100, pp. 195-210.
Akbarov, S. D.; Negin, M.(2017): Near-surface waves in a system consisting of a covering layer and a half-space with imperfect interface under two-axial initial stresses.Journal of Vibration and Control,vol. 23, no. 1, pp. 55-68.
Barshinger, J. N.; Rose, J. L.(2004): Guided wave propagation in an elastic hollow cylinder coated with a viscoelastic material.ieee transactions on ultrasonics,ferroelectrics, and frequency control,vol. 51, no. 11, pp. 1547-1556.
Carcione, J. M.(1992): Rayleigh waves in isotropic viscoelastic media.Geophysical Journal International,vol. 108, no. 2, pp. 453-464.
Chiriţă, S.; Ciarletta, M.; Tibullo, V.(2014): Rayleigh surface waves on a Kelvin-Voigt viscoelastic half-space.Journal of Elasticity, vol. 115, no. 1, pp. 61-76.
Ewing, W. M.; Jazdetzky, W. S.; Press, F.(1957):Elastic Waves in Layered Media.McGraw-Hill, New York.
Fan, J.(2004): Surface seismic Rayleigh wave with nonlinear damping.Applied Mathematical Modelling,vol. 28, no. 2, pp. 163-171.
Fung, Y. C.(1965):Foundations of solid mechanics. Prentice Hall.
Garg, N.(2007): Effect of initial stress on harmonic plane homogeneous waves in viscoelastic anisotropic media.Journal of sound and vibration,vol. 303, no. 3, pp. 515-525.
Jiangong, Y.(2011): Viscoelastic shear horizontal wave in graded and layered plates.International Journal of Solids and Structures,vol. 48, no. 16, pp. 2361-2372.
Kocal, T.; Akbarov, S. D.(2017): On the attenuation of the axisymmetric longitudinal waves propagating in the bi-layered hollow cylinder made of viscoelastic materials.Structural Engineering and Mechanics, vol. 61, no. 2, pp. 145-165
Kolsky, H.(1963):Stress waves in solids. Dover, New York.
Kumar, R.; Parter, G.(2009): Analysis of free vibrations for Rayleigh-Lamb waves in a microstretch thermoelastic plate with two relaxation times.Journal of Engineering Physics and Thermophysics,vol. 82, pp. 35-46.
Lai, C. G.; Rix, G. J.(2002): Solution of the Rayleigh eigenproblem in viscoelastic media.Bulletin of the Seismological Society of America, vol. 92, no. 6, pp. 2297-2309.
Manconi, E.; Sorokin, S.(2013): On the effect of damping on dispersion curves in plates.International Journal of Solids and Structures, vol. 50, no. 11, pp.1966-1973.
Mazzotti, M.; Marzani, A.; Bartoli, I.; Viola, E.(2012): Guided waves dispersion analysis for prestressed viscoelastic waveguides by means of the SAFE method.International Journal of Solids and Structures, vol. 49, no. 18, pp. 2359-2372.
Meral, F. C.; Royston, T. J.; Magin, R. L.(2009): Surface response of a fractional order viscoelastic halfspace to surface and subsurface sources.The Journal of the Acoustical Society of America, vol. 126, no. 6, pp. 3278-3285.
Meral, F. C.; Royston, T. J.; Magin, R. L.(2011): Rayleigh–Lamb wave propagation on a fractional order viscoelastic plate.The Journal of the Acoustical Society of America, vol.129, no. 2, pp. 1036-1045.
Negin, M.; Akbarov, S. D.; Erguven, M. E.(2014): Generalized Rayleigh wave dispersion analysis in a pre-stressed elastic stratified half-space with imperfectly bonded interfaces.CMC Comput Mater Continua,vol. 42, no. 1, pp. 25-61.
Negin, M.(2015): Generalized Rayleigh wave propagation in a covered half-space with liquid upper layer.Structural Engineering and Mechanics, vol. 56, no. 3, pp.491-506.
Pasternak, M.(2008): New approach to Rayleigh wave propagation in the elastic halfspaceviscoelastic layer interface.Acta Physica Polonica A,vol. 114, no. 6A, pp. 169-174.
Quintanilla, F. H.; Fan, Z.; Lowe, M. J.; Craster, R. V.(2015): Guided waves'dispersion curves in anisotropic viscoelastic single-and multi-layered media.InProc. R.Soc., vol. 471, no. 2183, pp. 20150268.
Rabotnov, Yu. N.(1980):Elements of hereditary solid mechanics.Mir, Moscow.
Sharma, J. N.(2005): Some considerations on the Rayleigh Lamb waves in viscoelastic plates.Journal of Vibration and Control, vol. 11, pp. 1311-1335.
Sharma, J. N.; Othman, M. I. A.(2007): Effect of rotation on generalized thermoviscoelastic Rayleigh-Lamb waves.International Journal of Solids and Structures,vol.44, pp. 4243-4255.
Sharma, J. N.; Kumar, S.(2009): Lamb waves in micropolar thermoelastic solid plates immersed in liquid with varying temperature.Mechanicca,vol. 44, pp. 305-319.
Sharma, J. N.; Sharma, R.; Sharma, P. K.(2009): Rayleigh waves in a thermoviscoleastic solid loaded with viscous fluid of varying temperature.International Journal of Theoretical & Applied Sciences,vol. 1, no. 2, pp. 60-70.
Sharma, M. D.(2011): Phase velocity and attenuation of plane waves in dissipative elastic media: Solving complex transcendental equation using functional iteration method.International Journal of Engineering Science and Technology,vol. 3, no. 2, pp. 130-136.
Vishwakarma, S. K.(2012): Gupta S. Torsional surface wave in a homogeneous crustal layer over a viscoelastic mantle.International Journal of Applied Mathematics and Mechanics,vol. 8, no. 16, pp. 38-50.
Zhang, K.; Luo, Y.; Xia, J.; Chen, C.(2011): Pseudospectral modeling and dispersion analysis of Rayleigh waves in viscoelastic media.Soil Dynamics and Earthquake Engineering,vol. 31, no. 10, pp. 1332-1337.
Appendix A
The expressions of the componentsαijin equation (21):
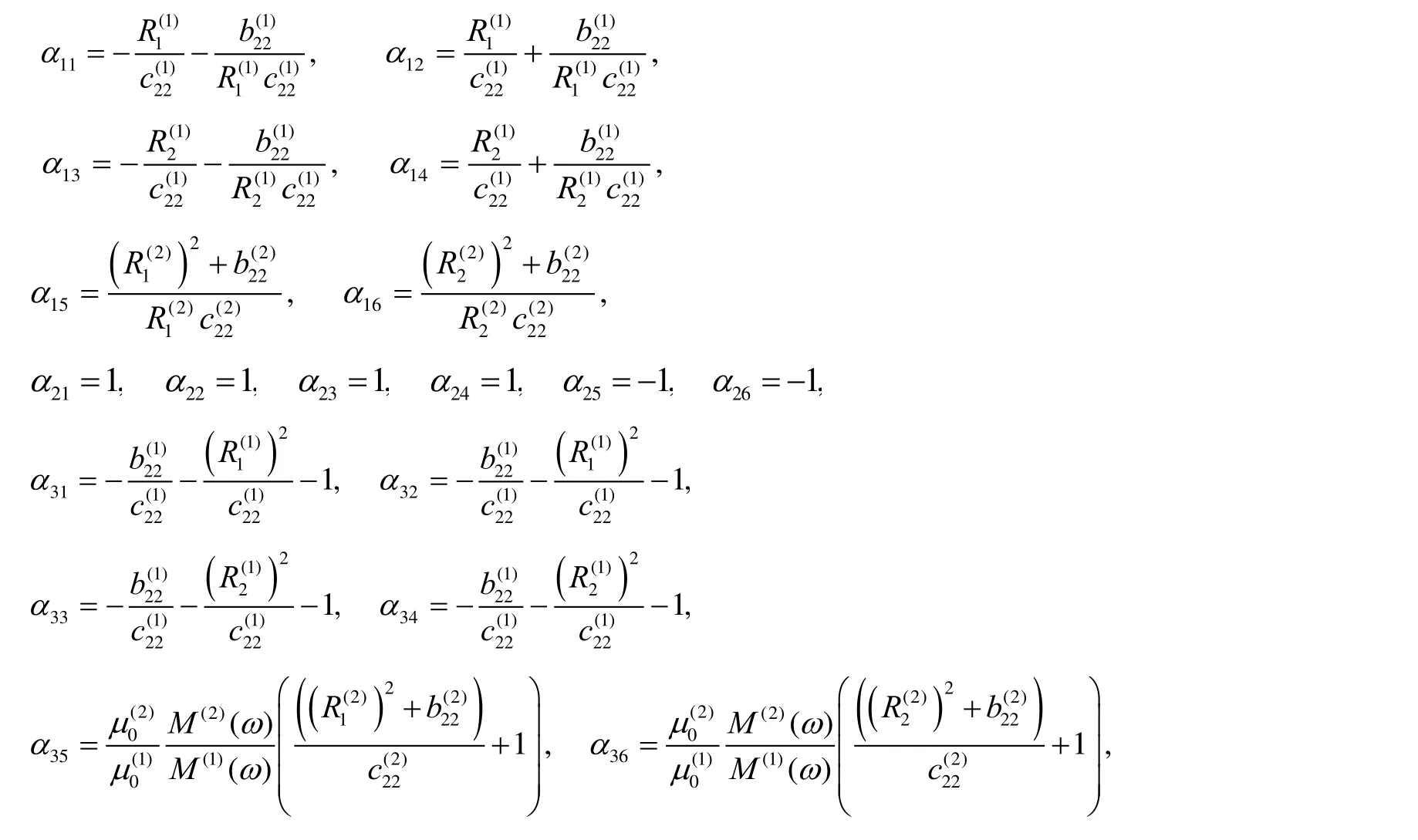


杂志排行
Computers Materials&Continua的其它文章
- Comparison of CS, CGM and CS-CGM for Prediction of Pipe’s Inner Surface in FGMs
- Low Velocity Impact Response and Failure Assessment of Textile Reinforced Concrete Slabs
- Research on SFLA-Based Bidirectional Coordinated Control Strategy for EV Battery Swapping Station
- Fingerprint Liveness Detection from Different Fingerprint Materials Using Convolutional Neural Network and Principal Component Analysis
