中承式钢管混凝土拱桥动力特性分析
2018-01-23吴梅容卓卫东
吴梅容, 卓卫东,2, 孙 颖,2, 谷 音,2
(1. 福州大学 土木工程学院,福州 350116; 2. 福州大学 福建省土木工程多灾害防治重点实验室,福州 350116)
钢管混凝土拱桥造型优美,又同时解决了拱桥高强度材料应用和施工两大难题,因此,在我国的西南、华南等地区得到大量工程应用[1-2];据最新统计,国内已建成主跨不小于50 m的钢管混凝土拱桥多达395座。可见,钢管混凝土拱桥是中、大跨径桥梁极具竞争力的桥型之一。在钢管混凝土拱桥结构体系中,以中承式钢管混凝土拱桥应用居多[3];然而,由于其悬吊桥道系常采用漂浮体系,桥梁整体性较差,结构振动问题较为突出,因此,深入研究这一类桥型的结构动力特性具有重要理论和实践意义。
中承式钢管混凝土拱桥设计参数较多,不同研究者对其结构动力特性的研究各有侧重。李玲瑶等[4]针对“K”撑和“米”撑两种横撑形式,分析了横撑数量及其位置对一座桁式中承式钢管混凝土拱桥结构动力特性的影响,发现拱脚横撑对面内基频的影响不大,而对面外基频的影响较大;拱顶横撑对面外基频、面内竖弯基频以及稳定性影响不大,而对扭转基频影响显著。连岳泉等[5]探讨了主拱肋核心混凝土标号、稳定拱肋外倾角度、横撑与斜撑布置形式以及拱肋与桥面联结区刚度对一座单拱肋外倾中承式钢管混凝土拱桥结构动力特性的影响,发现主拱肋核心混凝土强度的影响较小,稳定拱肋外倾角度、横撑与斜撑布置形式对拱肋振动有较大的影响,而拱肋与桥面联结区刚度变化会导致全桥结构动力特性的显著变化。云迪等[6]探讨了拱肋矢跨比、拱肋内倾角对一座大跨中承式钢管混凝土拱桥结构动力特性的影响,表明降低拱肋矢跨比或将拱肋内倾可提高结构的面外振动频率。吴庆雄等[7]讨论了主拱跨径、截面和桥道系结构对中、下承式钢管混凝土拱桥面内振动模态特性的影响,并基于Rayleigh法,提出了估算中、下承式钢管混凝土拱桥面内一阶反对称、对称振型的固有频率的实用公式。张武等[8]针对一整体性较差的在役大跨径中承式钢管混凝土拱桥,讨论了增设纵梁将悬吊桥面系改造为空间纵横梁框架体系后结构动力特性的改善。
与国内丰富的钢管混凝土拱桥研究与工程实践不同,国外对此类桥型的研究及工程应用都很少[9-14]。Yoshimura等采用现场振动试验和数值模型分析方法,对日本首座中承式钢管混凝土拱桥——新西海桥进行了动力特性分析,并与国内已建成的同类桥型的结构动力特性进行了比较,发现该桥具有良好的动力性能。
尽管国内外针对中承式钢管混凝土拱桥的结构动力特性已开展了一些研究,然而,这些研究绝大多数都是基于一座特定的实桥,因而研究结论具有一定的局限性。本文在统计分析158座国内已建成的中承式钢管混凝土拱桥设计资料的基础上,进行基准桥梁试设计;在此基础上,采用参数分析方法,着重探讨了矢跨比、宽跨比、主拱肋刚度、横撑布置方式、吊杆失效以及支座布置等对无推力中承式钢管混凝土拱桥结构动力特性的影响,从而为此类桥梁的结构动力响应分析及健康监测等提供必要的信息和研究基础。
1 中承式钢管混凝土拱桥设计参数统计分析
本文在文献[3]基础上,进一步收集国内已建成的中承式钢管混凝土拱桥的设计资料,总共得到了158座实桥的资料。限于篇幅,本文仅列出其中代表性的部分桥例,见表1。表1中,“/”表示缺乏具体信息,“一”表示“一”字形横撑,“K”和“米”分别表示“K”字形和“米”字形横撑(下同)。通过对此类桥型的主要结构设计参数的统计分析,为建立有推力和无推力中承式钢管混凝土拱桥的基准有限元模型提供基础数据。
1.1 跨径统计分析
中承式钢管混凝土拱桥有两种结构形式:有推力拱(单跨结构)和无推力拱(飞鸟式),图1给出了158座中承式钢管混凝土拱桥主拱跨径的统计结果。从图1可见,中承式钢管混凝土拱桥的主跨跨径集中分布在100~199 m内,其中位数跨径是150 m。对无推力拱,其边主跨比也是一个重要的设计参数;根据统计,飞鸟式结构边主跨比在0.164~0.424。
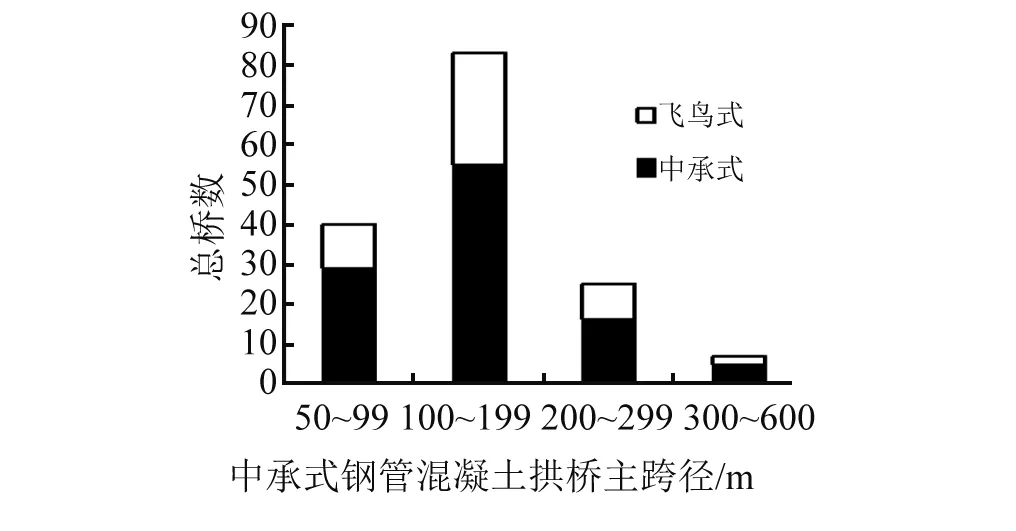
图1 主拱跨径分布Fig.1 Distribution histogram of main spans
1.2 矢跨比和矢高比统计分析
对有推力中承式钢管混凝土拱桥,其常用矢跨比为1/4、1/4.5和1/5,三者约占到总数的90%左右,如图2所示。对无推力中承式钢管混凝土拱桥,边拱的矢跨比取值一般在1/4.6~1/9.8,并且与主拱矢跨比的比值介于1/1.16~1/1.2,边拱的矢高与主拱矢高的比值集中分布在1/3.5~1/4.5内。

图2 有推力拱矢跨比分布Fig.2 Distribution histogram of ratio of rise-to-span
1.3 宽跨比统计分析
桥梁的桥面宽度主要取决于车流量,也与桥面布置相关。图3给出了跨径小于150 m与跨径在150 m及以上的中承式钢管混凝土拱桥宽跨比的统计结果。从图3可见,中承式钢管混凝土拱桥的宽跨比集中在0.05~0.25。
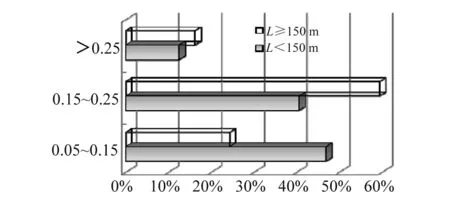
图3 宽跨比分布Fig.3 Distribution histogram of breadth to span
1.4 拱轴线型和拱轴系数统计分析
图4和图5分别给出中承式钢管混凝土拱桥的拱轴线型和拱轴系数取值的统计结果。从图4可见,中承式钢管混凝土拱桥常用的拱轴线型为悬链线和抛物线,其中悬链线所占比例约60%。从图5可见,拱轴系数与跨径之间的相关性不大;采用悬链线的中承式钢管混凝土拱桥的拱轴系数集中分布在1.2~1.7,且以1.5及附近的取值居多。
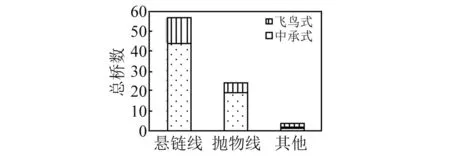
图4 拱轴线形统计Fig.4 Distribution histogram of arch axial line types

图5 拱轴系数与跨径关系Fig.5 Relationship between arch-axis coefficient and span
1.5 其他构造
除上述几个主要设计参数外,拱肋形式、横向联系、桥道系布置、吊杆等也是中承式钢管混凝土拱桥结构的重要组成部分。通过对158座实桥的调查发现,在跨径大于100 m的中承式钢管混凝土拱桥中,主拱肋截面形式通常以桁式居多;由于中承式钢管混凝土拱桥的横向稳定问题较为突出,因此,在横向联系的构造上,主要采用两种方式来解决横向稳定问题:一是设置不同形式的横撑(如“一”字形、“K”字形、 “X”字形、“米”字形等);二是采用拱肋内倾的提篮拱形式。此外,中承式钢管混凝土的立柱通常采用钢筋混凝土或钢管混凝土立柱(后者常用于大跨径或大矢跨比情况);吊杆一般采用平行的柔性吊杆,间距一般在4~8 m;桥道系早期多采用整体性较差的简支体系,目前主要采用先简支后连续的桥道系。
2 中承式钢管混凝土拱桥基准有限元模型
2.1 基准桥梁试设计
根据上节对中承式钢管混凝土拱桥主要设计参数与构造特征的统计分析结果,试设计了2座基准桥梁(分别记为基准桥梁Ⅰ和基准桥梁Ⅱ),其基本设计参数如表2所示。
试设计的基准桥梁Ⅰ为一净跨136 m、桥宽12 m的有推力中承式钢管混凝土拱桥,主拱横向平行设置两片桁式钢管混凝土拱肋,轴间距9 m。拱肋拱轴线型为悬链线,矢跨比为1/5,拱轴系数m=1.167;截面尺寸为3.0 m×1.6 m,弦杆采用4根φ550×8 mm的16Mn钢管,内灌C40混凝土,上下平联采用φ400×8 mm钢管,直腹杆和斜腹杆采用φ219×8 mm的钢管。在桥面以上设置3道“一”字式桁式横撑,桥面以下设置两道K撑。全桥共设13对吊杆,吊杆纵向间距8.1 m,采用110丝φ5高强钢丝。桥面系采用工字形横梁和T形纵梁(准连续结构),横梁间距8.1 m。
试设计的基准桥梁Ⅱ为无推力中承式钢管混凝土拱桥,其跨径布置为40 m+150 m+40 m,桥面宽度33 m。主跨为平行拱肋中承式钢管混凝土系杆拱桥,两侧边跨为上承式钢筋混凝土悬臂半拱,通过锚固于两侧边拱末端的系杆,使其成为自锚体系的中承式钢管混凝土拱桥。主拱肋拱轴线型为悬链线,矢跨比为1/5,拱轴系数m=1.3;由横向平行设置的两片四肢钢管桁架式拱肋组成,横向轴间距19.5 m。拱肋截面尺寸为3.65 m×2.10 m,标准段弦杆采用φ850×14 mm钢管,钢管内灌注C50混凝土,在拱脚段外包C50混凝土。边拱肋为半悬臂拱,拱轴线型为悬链线,矢高比为1/8.097,拱轴系数m=1.3。边拱采用劲性骨架混凝土结构,截面尺寸为2.6 m×2.5 m。主跨肋间共设置5道风撑,风撑纵向间距20 m。每道风撑为“一”字型空钢管桁架,截面尺寸为3.3 m ×2.7 m;主管采用φ500×12 mm 钢管,Q345C钢,风撑支管采用φ299×10 mm钢管。吊杆纵向间距5 m,采用高强钢丝吊索索体与高强钢拉杆通过连接器连接,吊索为121丝φ7高强平行钢丝束。
2.2 基准有限元模型的建立
采用Midas Civil软件,建立了2座基准桥的动力有限元模型,如图6所示。基准桥有限元模型中,拱肋弦杆、腹杆、横撑、桥墩、立柱均采用三维梁单元模拟;采用等效梁格法,在不考虑桥面铺装刚度贡献的条件下,将桥面系等效为由纵梁和横梁组成的梁格体系,并采用三维梁单元模拟;吊杆采用只受拉的杆单元模拟。对有推力结构(基准桥梁Ⅰ),通过主从约束关系模拟边梁与支座之间的联接,且不考虑桩-土-结构相互作用,有限元边界取在拱脚处,并视为固结边界。对无推力结构(基准桥梁Ⅱ),采用刚性连接单元模拟支座,并根据约束方向的要求确定各方向约束刚度,采用“m”法考虑桩-土-结构相互作用。
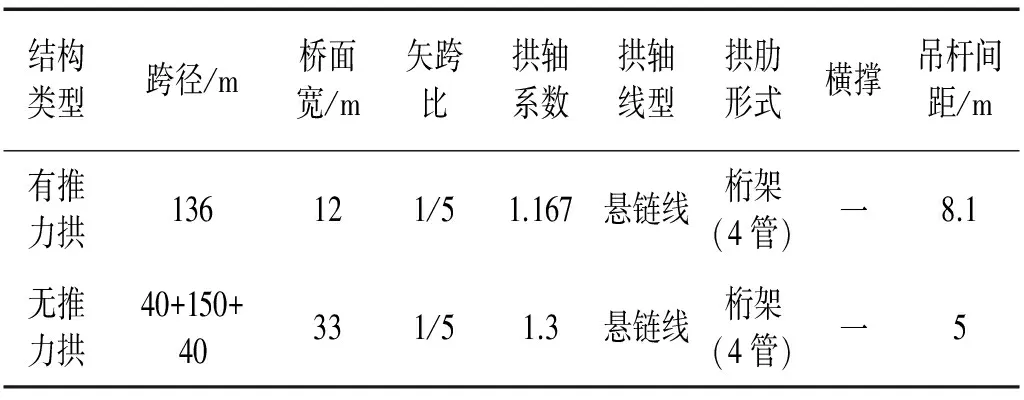
表2 基准桥梁基本设计参数

(a) 有推力结构
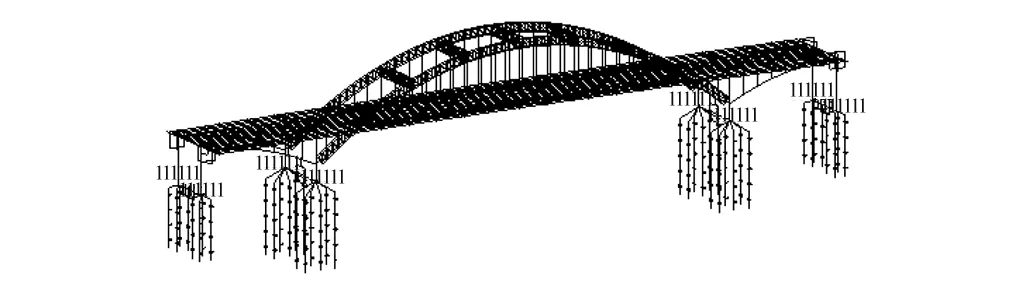
(b) 无推力结构图6 基准桥有限元计算模型Fig.6 FE models for the benchmark bridges
3 结构动力特性分析
3.1 有推力与无推力基准桥结构动力特性比较
根据图6所建立的2座基准桥的动力有限元模型,分别计算了其结构动力特性。表3列出了有推力与无推力基准桥前十阶的自振频率与振型特征。从表3可以发现,2座基准桥的基本自振周期均在1.5 s以上,均属于柔性结构;其前十阶的振动形态表现为面外振动、面内振动以及空间扭转振动,且高阶振动模态较为密集,桥面板、拱肋有较为明显的耦合振动特点。从出现次序上看,无论是有推力或无推力结构,其面外振型均较早出现,说明中承式钢管混凝土拱桥结构的横向稳定问题较为突出;与无推力结构相比,有推力结构的面外侧弯振型出现在桥面竖弯振型之前,说明有推力结构的横向刚度与竖弯刚度之比相对较小;另外,从振型质量参与系数上看,高阶振型对无推力结构的动力响应影响较大。
3.2 无推力中承式钢管混凝土拱桥动力特性参数分析
在基准桥结构动力特性分析的基础上,本文进一步以无推力中承式钢管混凝土拱桥为研究对象,探讨矢跨比、宽跨比、主拱肋刚度、横撑布置方式、吊杆失效以及支座布置等对结构动力特性的影响。在进行参数分析时,不考虑各参数之间的耦合效应,仅改变基准桥梁Ⅱ中的某一参数,其它参数保持不变。
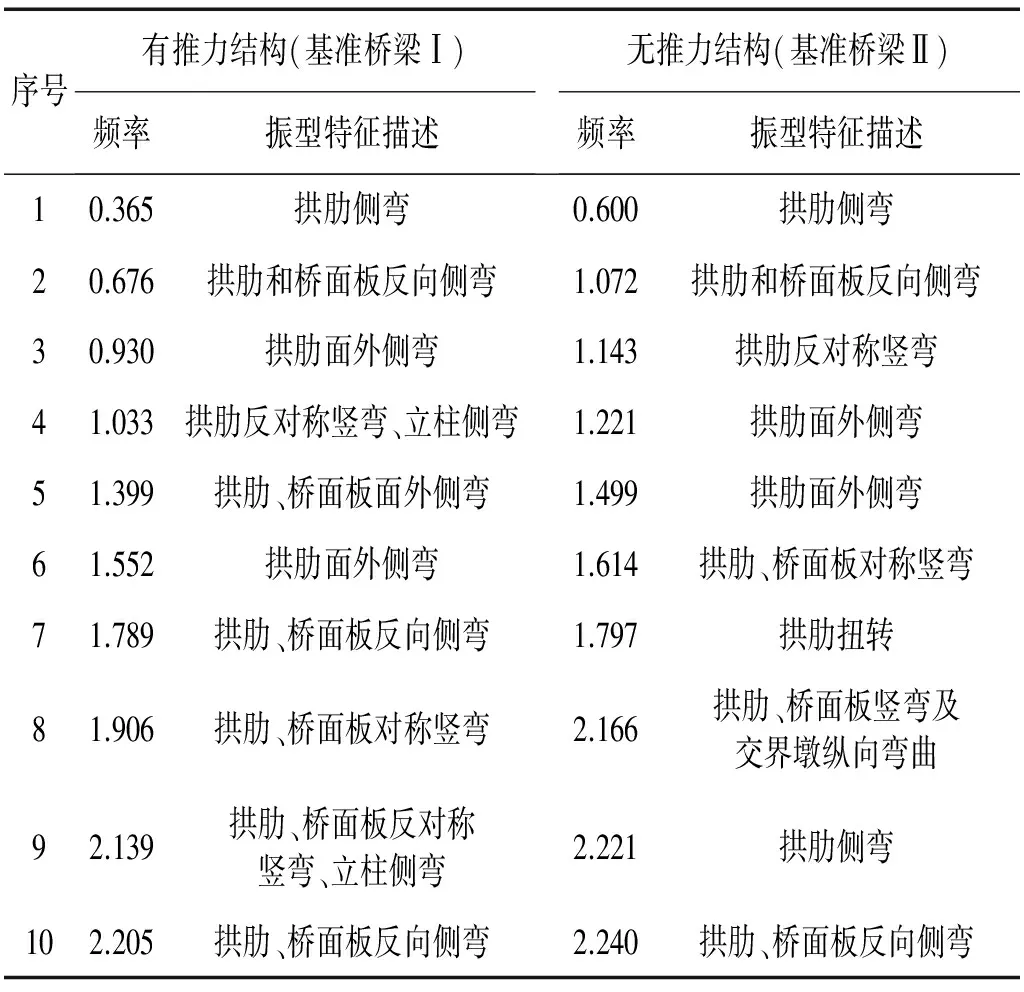
表3 有推力与无推力基准桥前十阶模态比较
(1) 矢跨比影响分析
在分析矢跨比变化对结构动力特性的影响时,选取的矢跨比参数分别为1/5(基准桥)、1/4.5及1/4,图7绘出了相关的计算结果。从图7可见,矢跨比变化对主拱肋低阶竖弯振动频率的影响很小,对主拱肋一阶侧弯及一阶扭转振动频率的影响相对较大,且一阶侧弯及一阶扭转振动频率均随矢跨比的增大而减小。分析表明,在本文选取的矢跨比变动范围内,矢跨比变化不会改变结构低阶振型及其出现次序;此外,矢跨比变化引起主拱肋一阶侧弯振动频率的变化幅度最大,降幅为7.5%。

图7 矢跨比变化对结构动力特性的影响Fig.7 Influence of rise-span ratio to dynamic properties
(2) 宽跨比影响分析
在分析宽跨比变化对结构动力特性的影响时,选取的宽跨比参数分别为0.07、0.1、0.13、0.18,图8绘出了相关的计算结果。由图8可见,宽跨比变化对主拱肋一阶侧弯及一阶反对称竖弯振动频率的影响很小,对主拱肋一阶对称竖弯及一阶扭转振动频率的影响相对较大,且一阶对称竖弯及一阶扭转振动频率均随宽跨比的增大而减小。分析表明,在本文选取的宽跨比范围内,宽跨比变化也不会改变结构低阶振型及其出现次序;此外,宽跨比变化引起主拱肋一阶扭转振动频率的变化幅度达11.4%。这表明增大桥面宽度,可明显改善无推力结构的横向稳定性。

图8 宽跨比变化对结构动力特性的影响Fig.8 Influence of width to span ratio to dynamic properties
(3) 主拱肋刚度影响分析
在分析主拱肋刚度变化对结构动力特性的影响时,主拱肋刚度变化是通过改变材料弹性模量的方法实现的,图9绘出了相关的计算结果。由图9可见,主拱肋刚度改变对各阶自振频率的影响也很小,可忽略不计。分析表明,主拱肋刚度改变同样不会改变结构的低阶振型及其出现次序。
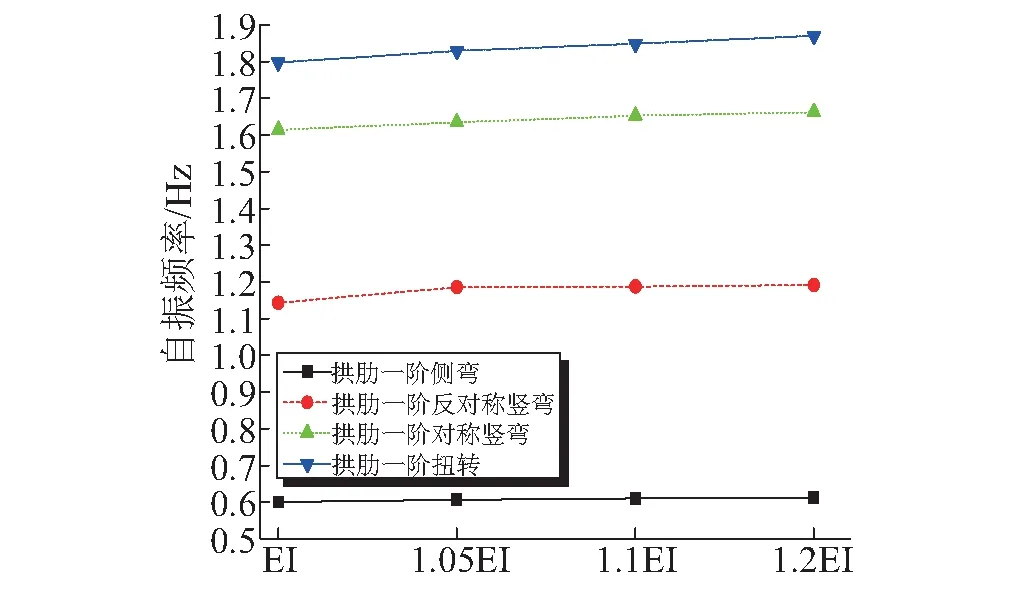
图9 主拱肋刚度变化对动力特性的影响Fig.9 Influence of arch rib stiffness to dynamic properties
(4) 横撑布置方式影响分析
横撑布置方式的改变主要从两个方面予以考虑:一是位置,二是数量。基准桥梁Ⅱ在桥面以上共设置5道横撑(见图6(b),沿纵桥向编号依次为1~5),在考虑横撑布置方式对结构动力特性的影响时,本文还计算分析了与基准桥梁Ⅱ不同的3种横撑布置方式:①去除1号和5号横撑;②去除2号和4号横撑;③去除拱顶的3号横撑。表4列出了相关的计算结果。分析表明,横撑数量对主拱肋面外振动频率与扭转振动频率的影响较大;不同位置的横撑对结构动力特性的影响程度不同,越靠近桥面的横撑对侧倾刚度的贡献越大,根据计算结果,当去除1号和5号横撑时,拱肋一阶侧弯频率减小了15%;而拱顶横撑对结构动力特性的影响较小,仅在一定程度上增大了拱肋的侧弯频率。另外值得注意的是,横撑间距变化对中承式钢管混凝土拱桥的面外弯曲刚度影响较大,与基准桥相比,去除2号和4号横撑时,第5阶与第8阶自振频率分别下降了5%和10%。
(5) 吊杆失效影响分析
本文在探讨吊杆失效对结构动力特性的影响时,考虑了3种失效模式:①基准桥梁Ⅱ主拱肋两侧3根边吊杆失效;②基准桥梁Ⅱ主拱肋单侧3根边吊杆失效;③基准桥梁Ⅱ全桥半数吊杆失效,即吊杆间距为基准桥的2倍。表4列出了相关的计算结果。分析表明,吊杆失效对结构自振频率的影响不可忽略;与基准桥相比,在吊杆半数失效的情况下,主拱肋一阶对称竖弯及一阶扭转振动频率的减小幅度约为10%。
(6) 支座布置影响分析
在讨论支座布置方式对结构动力特性的影响时,将基准桥梁Ⅱ中交界墩一侧的单向盆式支座改为固定支座,其余参数保持不变,计算结果见表5。分析表明,支座布置方式对结构振型的影响较大。与基准桥相比,支座布置方式改变后,结构的前7阶振型保持不变,然而,后续部分振型在出现次序上发生了变化;从其对自振频率的影响看,各阶自振频率的变化幅度均在5%以内。

表4 不同横撑布置方式及吊杆失效方式下前10阶自振频率计算结果Tab.4 Results of first 10 natural frequencies considering various arrangements of transverse braces and failure modes of suspenders Hz

表5 支座布置方式改变前后结构的动力特性
4 结 论
(1) 大跨径中承式钢管混凝土拱桥具有密集高阶模态的特点,且桥面板、拱肋的耦合振动较为明显。
(2) 对有推力和无推力大跨径中承式钢管混凝土拱桥,其面外振型较早出现,表明此类结构的横向稳定问题较为突出;与无推力体系相比,有推力体系高阶振型对结构动力性能的影响较小。
(3) 在常用取值范围内,矢跨比、主拱肋刚度以及支座布置方式和吊杆失效对无推力中承式钢管混凝土拱桥结构动力特性的影响较小。
(4) 对无推力中承式钢管混凝土拱桥,横撑布置方式对拱肋侧弯频率的影响较大,可影响结构横向稳定性;增大桥面宽度,可明显改善无推力结构的横向稳定性。
[ 1 ] 陈宝春. 钢管混凝土拱桥 [M]. 2版. 北京: 人民交通出版社, 2007.
[ 2 ] CHEN B C, WANG T L. Overview of concrete filled steel tube arch bridges in China[J]. Practice Periodical on Structural Design and Construction, 2009, 14(2): 70-80.
[ 3 ] 陈宝春, 刘福忠, 韦建刚. 327座钢管混凝土拱桥的统计分析[J]. 中外公路, 2011, 31(3): 96-103.
CHEN Baochun, LIU Fuzhong, WEI Jiangang. Analysis of 327 concrete-filled steel tube arch bridges[J]. Journal of China & Foreign Highway, 2011, 31(3): 96-103.
[ 4 ] 李玲瑶, 陈政清, 葛耀君. 钢管混凝土拱桥拱肋横撑对动力和稳定性的影响[J]. 公路交通科技, 2008, 25(3): 70-74.
LI Lingyao, CHEN Zhenqing, GE Yaojun. Effects of arch rib cross bars on dynamic and stabilization characteristics of concrete filled steel tubular arch bridge[J]. Journal of Highway and Transportation Research and Development, 2008, 25(3): 70-74.
[ 5 ] 连岳泉, 梁群. 单拱肋外倾式钢管混凝土拱桥动力特性分析[J]. 武汉理工大学学报, 2012, 36(5): 984-987.
LIAN Yuequan, LIANG Qun. Dynamic characteristics analysis of extroversion CFST arch bridge with single rib[J]. Journal of Wuhan University of Technology, 2012, 36(5): 984-987.
[ 6 ] 云迪, 刘贺, 张素梅. 大跨中承式钢管混凝土拱桥的自振特性及稳定性[J]. 吉林大学学报(工学版), 2013, 43(1): 86-91.
YUN Di, LIU He, ZHANG Sumei. Natural vibration and stability of large-span half-through concrete filled steel tubular arch bridge[J]. Journal of Jilin University (Engineering and Technology), 2013, 43(1): 86-91.
[ 7 ] 吴庆雄, 黄宛昆, 陈宝春. 中、下承式钢管混凝土拱桥面内振动模态分析[J]. 工程力学, 2012, 29(11): 221-227.
WU Qingxiong, HUANG Wankun, CHEN Baochun. Modal analysis of in-plane vibrations for half-through and through concrete-filled steel tubular arch bridges[J]. Engineering Mechanics, 2012, 29(11): 221-227.
[ 8 ] 张武, 吴运宏. 钢管混凝土拱桥动态悬吊式主梁结构改造技术[J]. 桥梁建设, 2016, 46(2): 103-108.
ZHANG Wu, WU Yunhong. Rehabilitation techniques for dynamically suspended main girder structure of a CFST arch bridge[J]. Bridge Construction, 2016, 46(2): 103-108.
[ 9 ] YOSHIMURA M, WU Q, TAKAHASHI K, et al. Vibration analysis of the second Saikai bridge—a concrete filled tubular (CFT) arch bridge[J]. Journal of Sound & Vibration, 2006, 290(1/2): 388-409.
[10] BRADFORD M A, PI Y L, QU W L. Time-dependent in-plane behaviour and buckling of concrete-filled steel tubular arches[J]. Engineering Structures, 2011, 33(5): 1781-1795.
[11] PI Y L, BRADFORD M A, QU W L. Long-term non-linear behaviour and buckling of shallow concrete-filled steel tubular arches[J]. International Journal of Non-linear Mechanics, 2011, 46(9): 1155-1166.
[12] MORCOUS G, HANNA K, DENG Y, et al. Concrete-filled steel tubular tied arch bridge system: application to Columbus viaduct[J]. Journal of Bridge Engineering, 2012, 17(1): 107-116.
[13] CHEN W F, DUAN L. Bridge engineering handbook [M]. 2nd ed. Florida: CRC Press, 2013.
[14] LAI Z C, VARMA A H, ZHANG K. Noncompact and slender rectangular concrete-filled steel tube (CFT) members: experimental database, analysis, and design[J]. Journal of Constructional Steel Research, 2014, 101: 455-468.
