一种6轴工业机器人的结构设计与运动学建模

（广东交通职业技术学院 机电工程系，广州 510800）

0 引言

6轴机器人是工业机器人应用最为广泛的一种类型[1]。机器人本体结构设计是实现机器人功能的基础，德国库卡（KUKA）机器人公司、瑞士ABB公司、日本FANUC公司等所研制的6轴串联机器人几乎具备了人类手臂的全部操作功能，但6轴机器人由于大多是垂直旋转关节，很多时候会出现多轴共线自由度退化的问题，因此此类机器人在诸如焊接的时候，需要从不同的姿态多次焊接，造成焊接时间和质量严重下降。

机器人运动学分析是实现机器人运动控制与轨迹规划的基础，其中正运动学分析是最基本的问题[2]，而D-H法[3～5]是常用的分析方法，通过仿真可以模拟机器人的运动情况，验证建立的运动学模型。针对自由度退化，机器人出现奇异点的问题，虽然出现多种解决算法，但是并不能达到完全根除。日本OTC进行了研究，因此推出了特异型5轴6自由度机器人[6,7]。另外通用6轴机器人在焊接的时候任意时间多要通过6轴联动试验位姿的插补，因此能耗较大。国外机器人公司从能耗入手提出了很多新颖的机器人，如SCARA机器人等[8～10]。

针对上述的问题，本文提出的新型机器人结构采用5串联关节+1移动关节的方式组成机器人的本体。具体分配是1、2、3轴为串联，4轴为平移轴，5、6轴为串联轴通过第四轴的平移可以解决臂展的问题及避免机器人退化的问题。

1 6轴机器人的结构

本文提出的6轴机器人是由5个串联轴加一个平移轴组成，机器人1、2、3、5、6轴为旋转轴，4轴为平移轴，通过4轴的平移可以改变机器人的臂展。这样机器人的工作区间就是一个球体和圆柱体的结合体，工作范围加大。利用SolidWorks建立的6轴机器人结构如图1所示，轴1由基座内的交流伺服电机（轴1电机）和谐波齿轮组成，实现立柱回转；轴2由肩部的交流伺服电机（轴2电机）和谐波齿轮组成，实现肩关节旋转；轴3由肩部的交流伺服电机（轴3电机）和谐波齿轮组成，实现肘部转动；轴4以小臂中心线为轴线，由交流伺服电机（轴4电机）、联轴器和滚珠丝杠组成，实现手臂的平移运动。为减小转动惯量，电机安装在肘关节处，和肘关节电机交错安装；轴5由交流伺服电机（轴5电机）、同步带、谐波齿轮组成，电机安装在小臂内部末端。实现手腕俯仰P运动，P轴和Y轴（滚珠丝杠）的轴线垂直；轴6由交流伺服电机（轴6电机）、谐波齿轮和法兰盘组成，电机安装在腕部。实现手腕翻转R运动，P轴和R轴的轴线垂直，末端执行器通过法兰盘安装在末端。

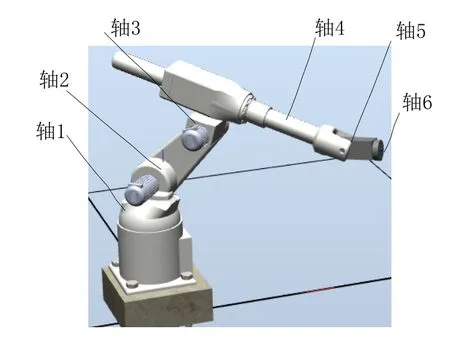
图1 机器人结构图

为确保6-DOF机器人运动学算法可靠、高的定位精度，建样机时应满足轴1旋转轴（基座旋转轴）、轴4平移轴、轴6旋转轴在同一个平面内；轴2旋转轴、轴3旋转轴以及轴5旋转轴互相平行，而且与前面提到的平面垂直；还需要保证轴4平移轴线、轴5旋转轴线以及轴6旋转轴线相交于一点。如果机器人的结构与此差别较大，难以满足实际的应用。

2 机器人正向运动学建模

机器人正运动学是利用连杆参数表示出末端执行器位姿的过程。下面使用D-H坐标系建立的方法先制定D-H参数表格，如表1所示。

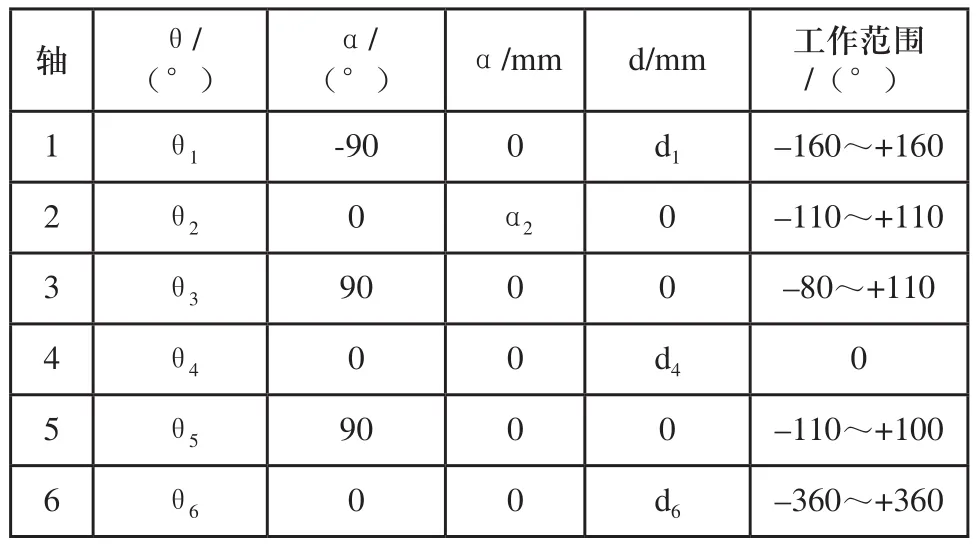
表1 6轴机器人D-H坐标参数

机器人D-H坐标转换公式：

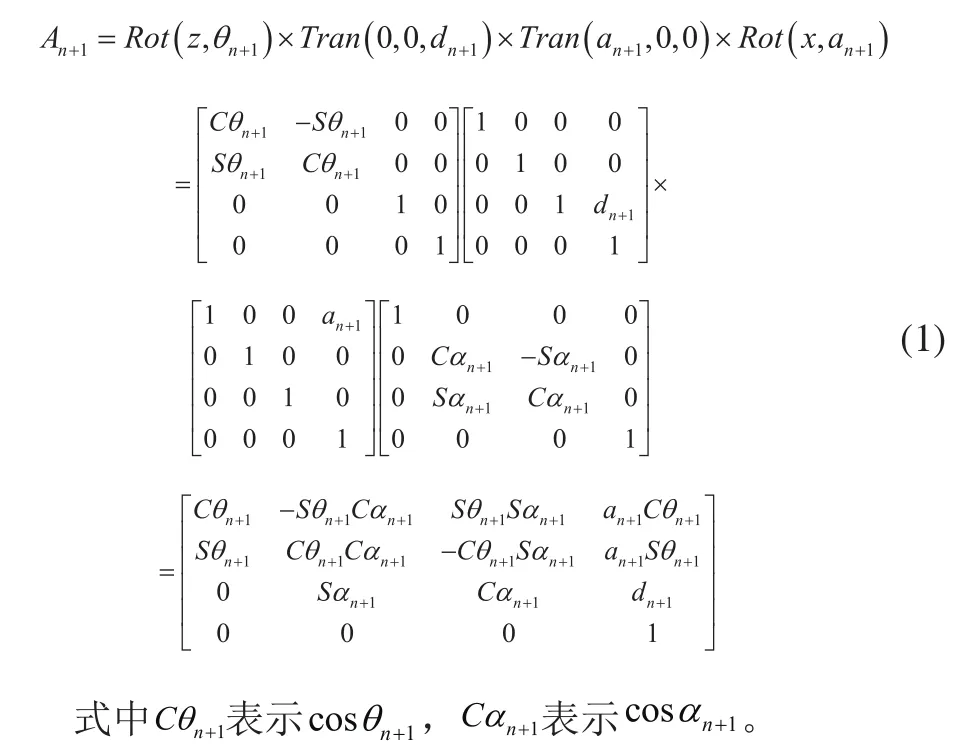
根据式(1)可得出：

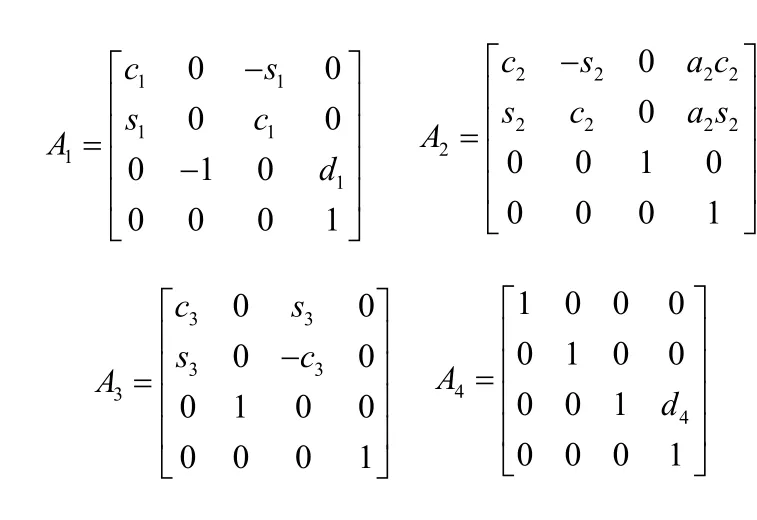
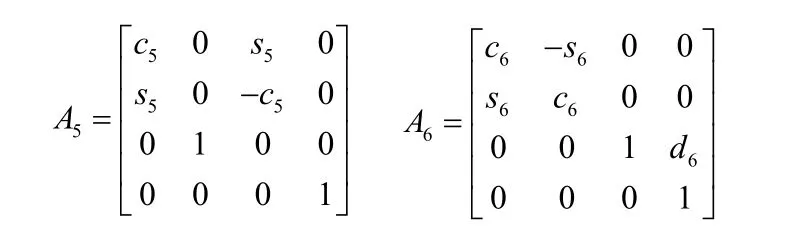
机器人的基座与手之间的总变换则为：

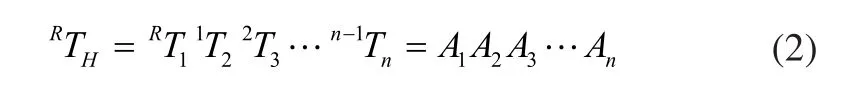
根据式(2)，得出机器人正运动学方程：

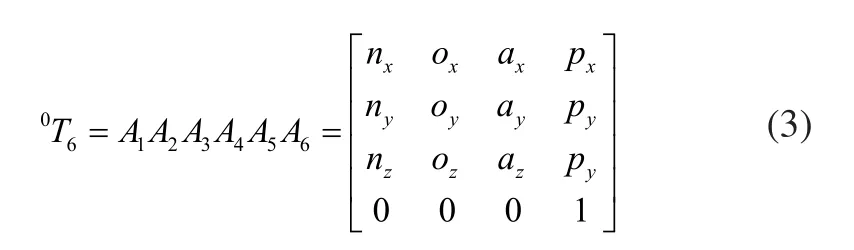
式中：

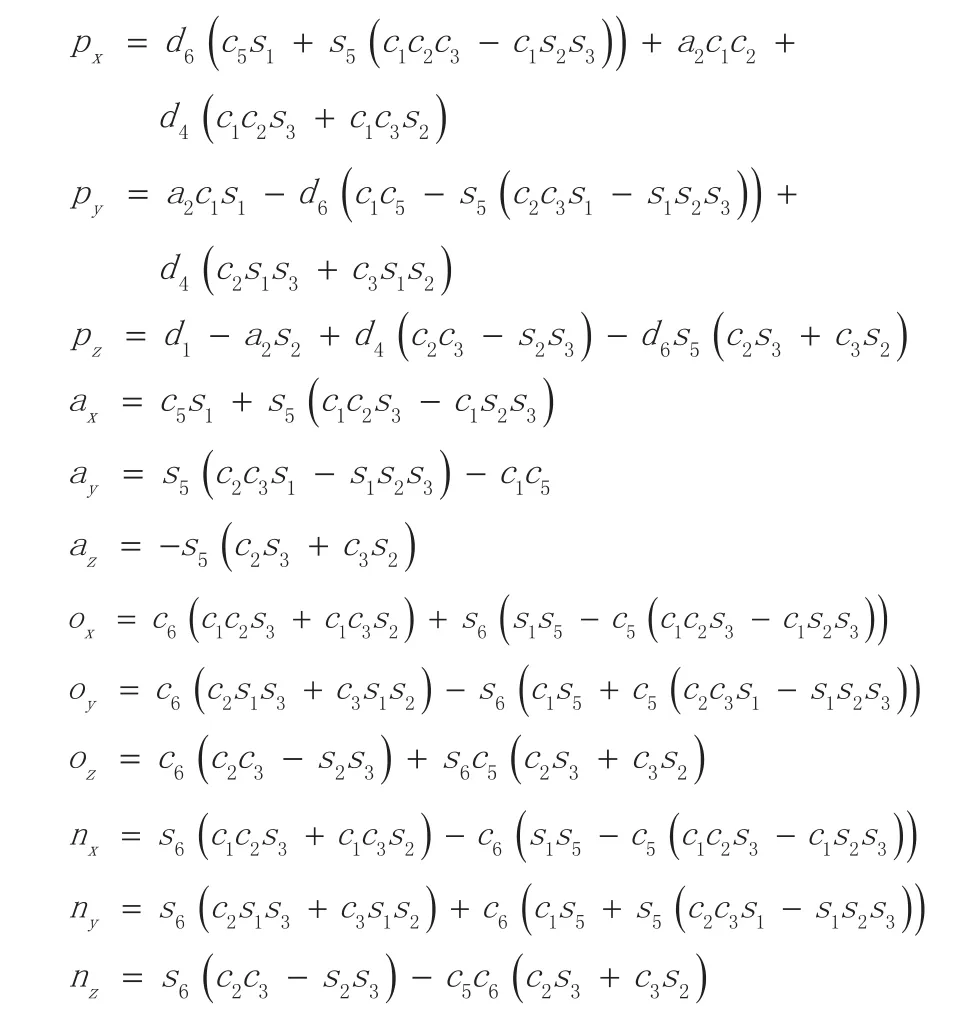
式(3)即为机器人的正运动学方程，可以通过给定各个关节变量来求得机器人末端执行器的位姿。

3 正向运动学验证

Robot toolbox是一个专门用来做机器人仿真的软件包，运行在MATLAB环境下，取机器人的结构参数，a2=0.3，d1=0.2，d6=0.1，根据正运动学方程式(3)，进行验证，部分软件代码如下：

将θ1=-0.2，θ2=-0.1，θ3=0.2，θ5=0.1，θ6=0.6，d4=0.5输入机器人驱动窗口如图2中的q1，q2，q3，q4，q5，q6，此时机器人驱动位姿效果如图3所示。同时在图2中生成机器人6轴法兰中心仿真位姿：

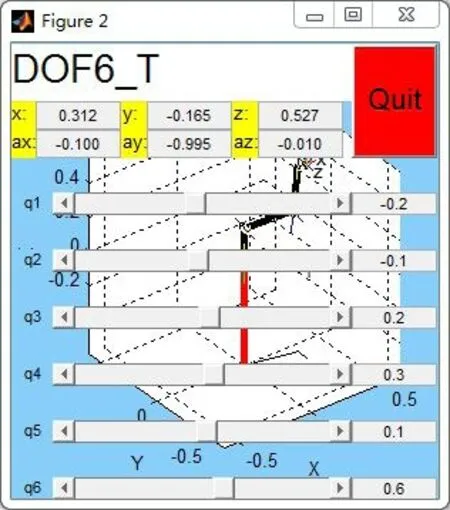
图2 模拟驱动图

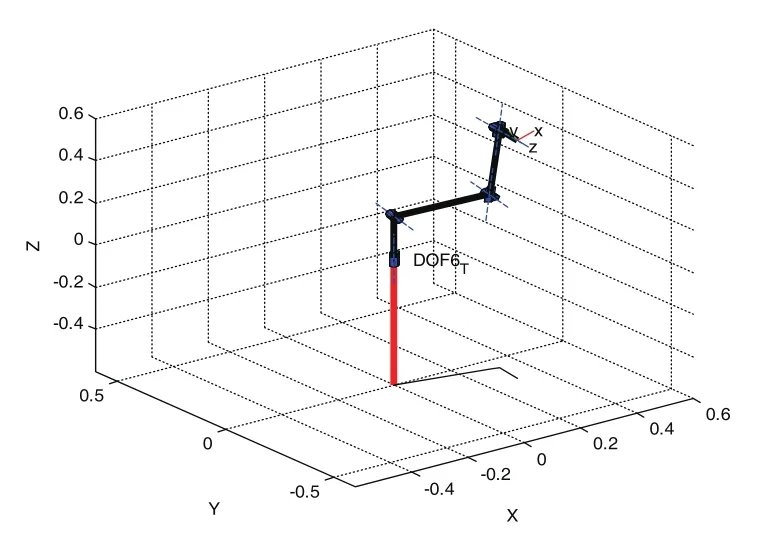
图3 机器人位姿图

为保证论证机器人正运动学模型正确的严谨性，并使机器人位姿差异尽可能的大，再取2组机器人角度值如图4和图5所示。

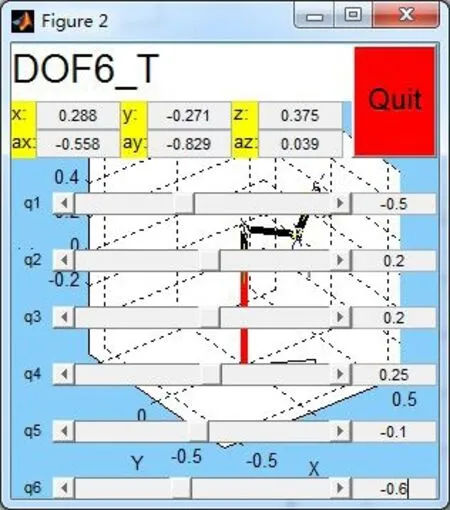
图4 模拟驱动图

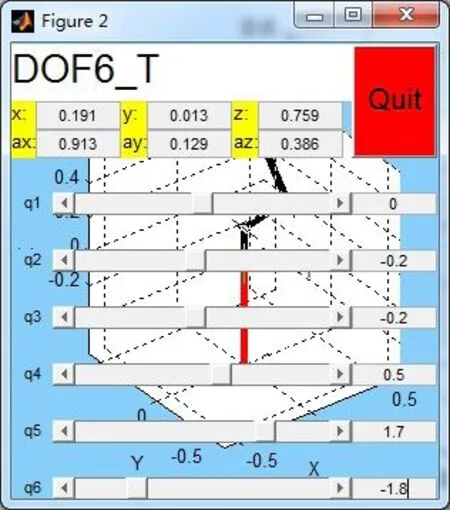
图5 模拟驱动图

根据机器人的正运动学方程式(3)，利用Robotics toolbox建立Dof6_fkine函数，并代入三种情况旋转关节角度和平移关节值，可得出机器人6轴法兰中心计算位姿。其三种情况理论计算位姿和Robotics计算位姿对比如表2、表3和表4所示。

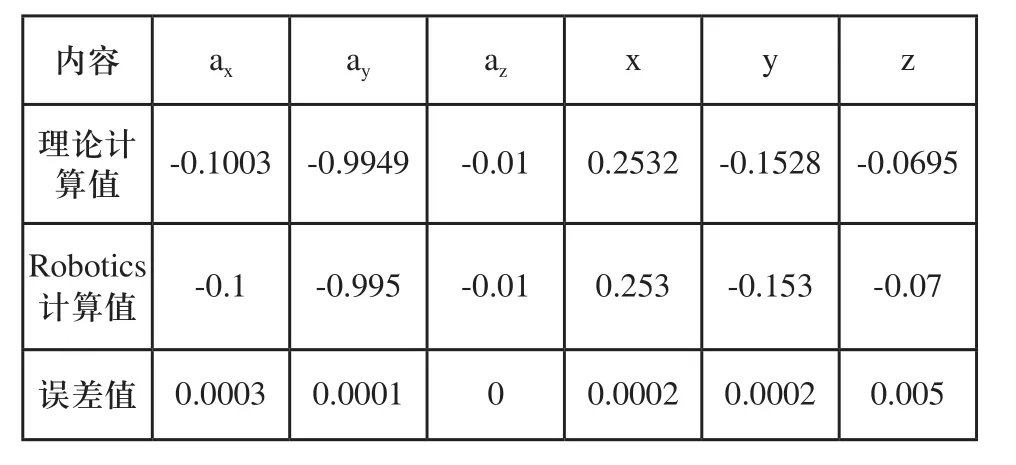
表2 理论计算值与Robotics计算值对比表

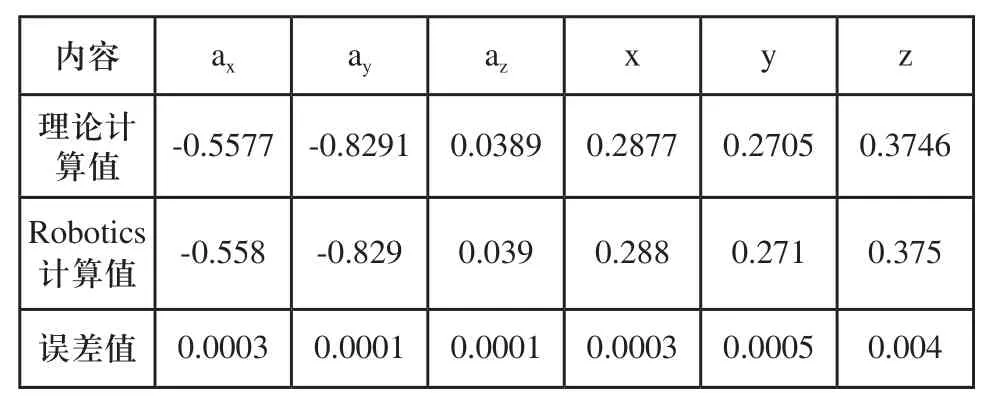
表3 理论计算值与Robotics计算值对比表

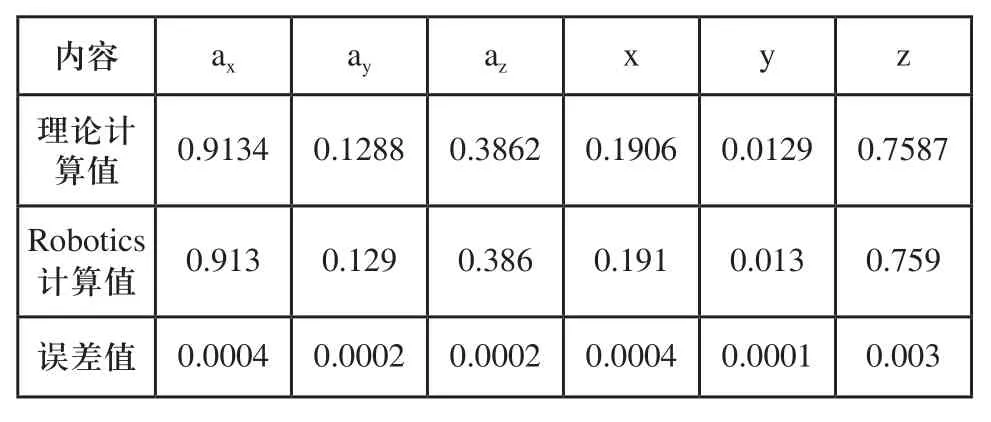
表4 理论计算值与Robotics计算值对比表

数据分析，计算位姿的数据是小数点后四位，实际机器人运行时的精度只能到后三位，因此图3、4、5窗口仿真位姿显示的数据是经过四舍五入的。从三组数据计算结果可以看出，机器人的姿态角ax、ay、az，与机器人位置x、y、z的值误差较小，数量级在小数点后四位，对于机器人来说经过减速机之后角度偏差几乎可以忽略，因此经过验证正向运动学模型算法是正确的。

4 MATLAB箱体焊接仿真

运用MATLAB中的Robotics工具箱，仿真焊接一个长宽高为300mm×150mm×600mm的箱体如图6所示。

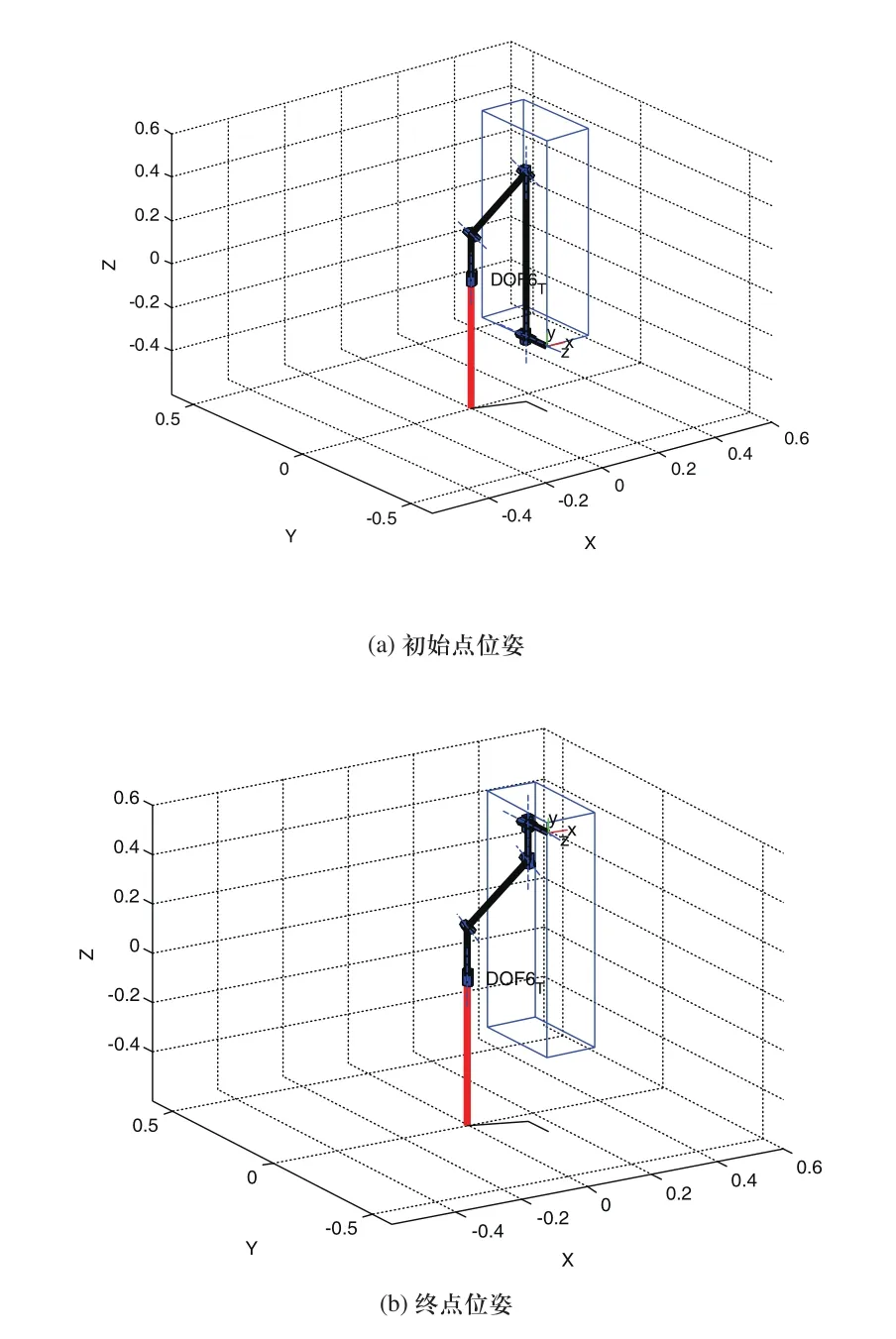
图6 箱体焊接仿真

仿真动作从底部（焊接起始点坐标X=-0.155，Y=-0.148，Z=-0.3）如图6(a)所示，向顶部（终止点坐标X=-0.155，Y=-0.148，Z=0.6）如图6(b)所示，焊接一条竖直的直线（插补间隔Z=0.05）逆解数据表如表5所示。

在箱体的底部机器人关节逆解为表5中第一行数据，在箱体顶部机器人6个关节的逆解为表3中最后一行数据。通过关节数据对比发现只有的d4值发生了变化，其他的关节值没有发生变化，因此焊接此条竖直焊缝是只有第四轴平移轴在运动。逆解表能够充分的说明在焊接类似的竖直焊缝时机器人的第四个关节只需要平移就可以完成，其他的关节不需要运动，但是在运动之前需要机器人首先将各个关节的角度调整到一定的角度。另外，焊接过程中不需要其他的关节运动，说明该机器人能够解决通用6-DOF机器人的奇异位姿不能到达的问题。

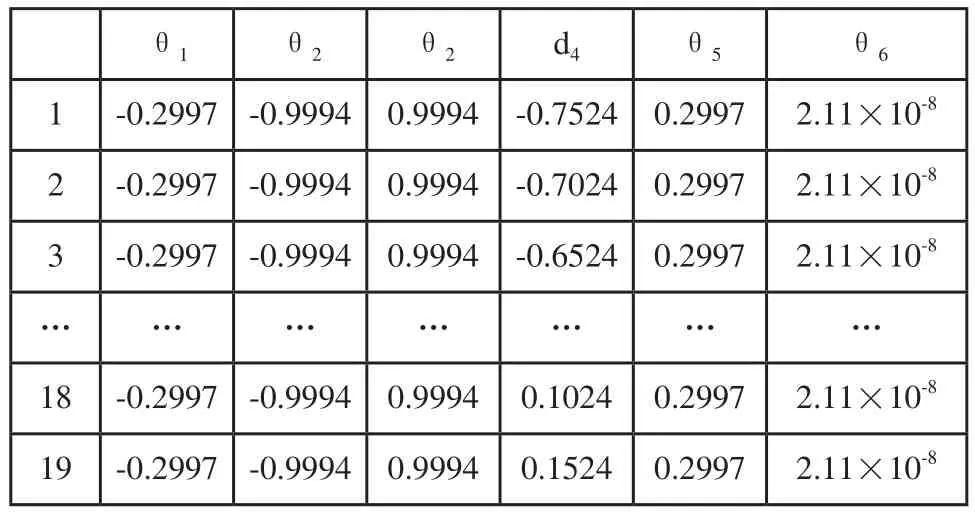
表5 逆解数据表

5 结论

本文提出了一种新型的机器人结构，此结构机器人由于第四轴为平移轴，一定程度上有效的避免了奇异位姿导致的无解和机器人自由度退化等问题。同时由于第四轴为平移轴，若采用高精度丝杆，可以大大的增加直线运动的轨迹精度，在未来的激光跟踪焊接中，焊接轨迹精度可达到0.001mm。另外，此机器人在焊接箱体结构的工件时，尤其是焊接直线时由6轴联动变为单轴运动，大大的降低了机器人的能耗。本机器人预计将在超高精度焊接领域发挥重要作用。

[1]潘磊,钱炜,张志艳,祁秋艳, PanLei, & QianWei等.四自由度机械臂运动学分析及matlab仿真[J].机械科学与技术,2013.32(3),115-119.

[2]刘晶晶,彭俊泉,刘新华.基于MATLAB的串并混联7-DOF仿人机械臂正运动学分析及仿真[J].机械传动,2015(7):59-62.

[3]熊有伦,唐立辛,丁汉.机器人技术基础[M].武汉:华中科技大学出版社,2008:8-200.

[4]Seling J M.机器人学的几何基础[M].北京:清华大学出版社,2008:150-200.

[5]JOHN J.CRAIG[美].机器人学导论:第3版[M].机械工业出版社,2006.

[6]Peter Corke.Robotics,Vision and Control[M].Berlin:Springer-Verlag Berlin and Heidelberg,2001:50-128.

[7]林义忠,欧爽翔.六自由度焊接机器人本体结构设计及动力学仿真[J].机械设计与制造,2014.6,21-23.

[8]刘 鹏,宋涛,贠超,高志慧.焊接机器人运动学分析及轨迹规划研究[J].机电工程,2013,290-294.

[9]邬亚兰.焊接机器人的轨迹规划与仿真研究[D].合肥:合肥工业大学,2011.

[10]卢锐,王忠庆.基于MATLAB Robotics Tools的机械臂仿真[J].电子世界,2014(18):417-418.