银杏树叶的气动特性研究

封伟建，邵传平

(中国计量大学 计量测试工程学院，浙江 杭州 310018)

树叶在风中受力变形并发生振动的现象，不仅在仿生学、建筑学、航天航空等领域具有显著的借鉴意义，同时在流固耦合、空气动力学研究方面也有着重要参考价值.人们利用树叶在轻微风力作用下即可发生振动的这一特性，发明了一种带有人工叶子以压电陶瓷材料为叶柄的发电“树”可以在很低的风速下工作.通过模拟树叶在风中变形振动制作的太阳能发电板，相比于普通的发电板能更好的适应风力较大的环境[1].此外，开展树叶气动特性的研究有助于人们了解树木整体的抗风能力.目前，人们针对树叶气动特性这一领域研究涉及较少，而且在已有的实验中大部分都是对整株树叶或整串树叶的研究．对于单片树叶气动特性的影响因素研究较少.

树叶的形状、尺寸大小以及叶柄的尺寸大小都会对树叶的气动特性产生影响.Shao[2]等对单片鹅掌楸树叶进行研究，得出鹅掌楸树叶在风速范围0～27 m/s内，依次存在低频摆动、飞翼状稳定、第一高频振动、堆形静止以及第二高频振动等五种状态，并通过对大量实验数据进行分析得出各个状态所对应的临界风速.

在空气阻力方面，Vogel[3]对红枫、鹅掌楸、核桃等多种树叶做了风洞实验研究，首次发现树叶在高风速下具有将叶片重构成堆形以减少空气阻力，达到自我保护的能力.叶片面积、形状和叶柄尺寸都是影响树叶阻力系数的重要因素.郑如侃[4]通过对梧桐树叶的研究发现，真实与人造的梧桐树叶都具有阻力系数随着雷诺数增大而逐渐减小并最终趋于稳定的特性，并通过实验发现梧桐树叶阻力系数最后稳定在0.1到0.3之间.Taneda[5]指出柔性体的变形并不总是引起阻力减小，有时也引起阻力增大. Schouveiler & Boudaoud[6]研究了塑料圆片阻力系数与所卷成堆角的关系.Albenl 等[7]发现一维柔性体的自相似变形使其阻力减少.Vogel测试了多种阔叶树树叶的阻力，发现与刚体阻力不同，树叶阻力D与风速U具有关系：

D～U2+α.

(1)

α被称为Vogel系数.在树叶受风振动方面，陈明[8]发现对于基于叶片长度的雷诺数也是影响树叶风振特性的重要参数.当杨树叶受风时，叶片经过静态变形，大幅低频振荡，叶片翻卷并重归静态，由静态变为大幅高频振动等不同状态．Speck[9]研究了芦竹在风中的形状重构及迎风面积变化.朱圆圆[10]对鹅掌楸树叶进行了研究发现鹅掌楸树叶的反面的抗风特性较正面更加优越，这与自然环境下真实树叶受风作用时多为反面迎风的情况相一致.

银杏树在我国各地区都有种植，完整的银杏树叶的形状酷似扇形其叶片角度在60度到200度的范围内不等，有的叶片中间凹入可达叶长的五分之四，相比于其他树叶银杏叶没有明显的主叶脉取而代之的细而密的二叉装平行叶脉，所以其易纵向撕裂，叶柄细而长，长度主要集中在3～8 cm之间.

本文旨在通过摄像、风洞天平和图像相关测振仪对不同银杏树叶以及人造银杏树叶在风洞的振动变形情况进行实验，寻找影响临界风速的因素与树叶状态突变对振动和阻力系数的影响.

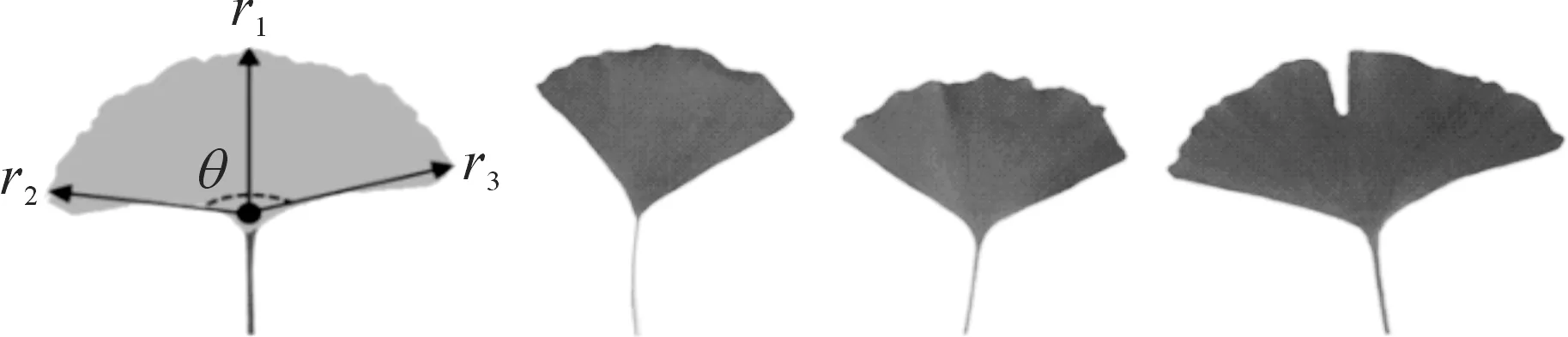
图1 叶片角度不同的银杏叶片Figure 1 Ginkgo leaves of different lamina angle

1 实验材料和方法

实验中我们以银杏叶柄与叶片的交点为圆心，找出银杏叶片上最上端、最左端、最右端的3个端点分别于圆心连线记做银杏叶片的半径r1、r2、r3，将r2与r3所夹的角记做银杏的叶片角θ.实验中所用到的银杏树叶均取自于中国计量学院校园及周边，每一片树叶都生长良好，健康无黄斑、无外来破损，尽可能排除因树叶自身损坏对实验产生的影响，采摘后的树叶置于清水中保存使用，最长保存时间为5小时(从采摘后开始)尽可能的保留树叶的原始特性.根据实验需求采集不同叶片角、叶片尺寸、叶柄长度的银杏树叶，尽可能的涵盖实验所要求的每一种类型，这样才更能增加实验的真实有效性.通过对多种材料进行测试我们发现利用PVC透明胶片纸制作的人造树叶能最好的反映真实树叶的气动特性(可以达到最理想的的效果)，根据实验需求我们可以选取厚度为0.07 mm、0.1 mm和0.125 mm的几种PVC材料.

实验中我们将树叶垂直固定在流场中间，使树叶正对来流方向(这就要求我们在选取树叶时注意树叶的叶柄和叶片尽可能的处于同一平面上).利用高速摄像机分别从正面与底面两个方向去拍摄记录下树叶在不同风速下的状态变化.在实验中要注意调整相机位置使之与树叶位置处于同一高度以确保叶片整个周期内的振动变形都处在拍摄区域内，拍摄的图像要清晰便于后期的处理. 风洞所提供的风速从0 m/s到29.2 m/s不等，根据实验需求逐渐增加风速.本实验中根据实际情况选择1.5 m/s左右的增加幅度.通过高速摄像机记录下真实树叶和人造树叶在不同风速下的振动变形情况，分析银杏树叶振动模态，找到临界风速与银杏树叶叶片角度、中间凹痕长度的关系，并分析影响树叶阻力系数发生变化的相关因素.

2 实验结果及分析

2.1 真实银杏树叶的稳定与振动模式分析

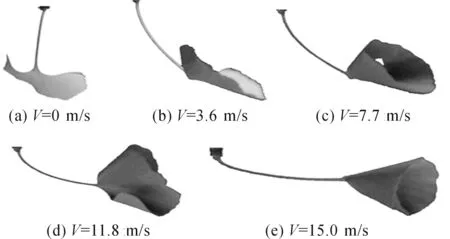
图2 银杏树叶受风作用时的振动与变形情况Figure 2 Vibration and deformation of ginkgo leaves in wind

通过对180片银杏树叶的摄像实验，我们发现银杏树叶在风速0～28 m/s内，叶片角较大的树叶主要经历了以下几个临界状态,分别为：静止稳定上扬，低频左右大幅整叶摆动或者高频小幅叶片部分上下振动，两侧叶片往中间合拢稳定，第一高频振动，S形稳定，第二高频振动，喇叭状稳定.叶片角较小的树叶，由高频振动直接过渡到喇叭状稳定，中间没有出现S形稳定状态.

如图2所示是银杏树叶在实验风速内的一个完整的变形振动周期，图2(a)是银杏树叶迎风时处于静止状态，图2(b)是随着风速的逐渐增大叶片逐渐抬高两侧翼顺来流方向卷幅逐渐增大.当树叶达到第一个临界风速时，树叶开始出现左右摆动的状态，继续增大风速达到第二个临界风速时树叶由左右摆动过渡到如图2(c)所示两侧翼往中间合拢的稳定飞翼状稳定.当达到第三临界风速时树叶由两翼上包稳定转变为第一次高频率的上下振动，图2(d)是树叶在第四临界风速时振动状态消失转变第二稳定状态S形侧向稳定，树叶S形稳定在风速达到第五临界状态是被破坏转变为第二次高频振动，并在风速达到第六临界风速时形成最终的图2(e)第三稳定状态喇叭状稳定.图2是银杏树叶受风作用下一个完整的状态变化，部分银杏树叶可能只存在其中部分临界状态.

图3 低风速与高风速下树叶的两种振动模式Figure 3 Two modes of vibration in the first critical state

通过大量实验我们发现无论是低风速还是高风速下，银杏树叶都存在着以下两种主要的具有周期性的振动模式.如图3(a)所示为在低风速下的第一种振动模式，此时叶柄不动叶片自身做高频低幅的上下扇动；图3(b)是在低风速下的第二种振动模式，此时叶柄受叶片影响随着叶片一起做低频大幅左右摆动.对于树叶高风速下的振动我们同样发现存在两种方式：图3(c)与(d)分别是树叶保持在高风速下重塑以后的结构做高频上下振动与左右摆动.

2.2 叶片角对银杏树叶的振动变形与临界风速的影响

我们发现在自然环境下不同银杏树上的银杏叶片的叶片角并不相同，即使是同一棵树上的银杏叶片其叶片角也各不相同，最小银杏树叶叶片角在60°左右，最大的约有200°，针对这一现象我们通过实验去分析不同叶片角大小是否会对银杏树叶的振动变形与临界风速产生影响.

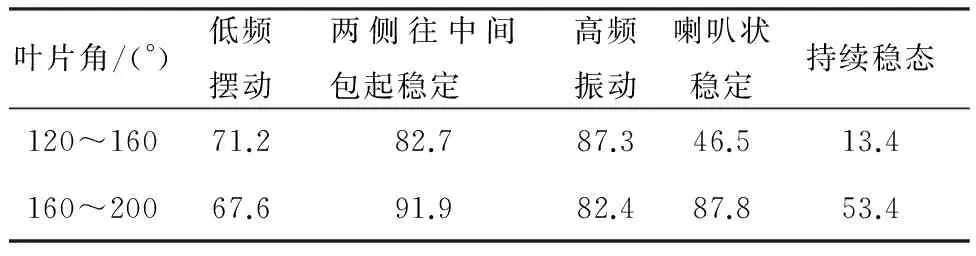
表1 不同叶片角的银杏树叶各状态出现的比例

通过实验发现当叶片角小于120°时，银杏树叶存在的状态比较单一，可用于分析的数据量比较少.为了更好更明显地分析叶片角对银杏树叶的振动变形与临界风速的影响，于是本文主要对叶片角大于120°存在较多临界状态的银杏树叶进行实验分析对比.通过对180片叶片角在120°～200°范围内的银杏叶片进行风洞实验并记录下不同风速时不同叶片角树叶各个临界状态存在的概率. 从表1我们可以发现在叶片角在160°～200°区间内的树叶中67.6%的叶片出现了低频摆动，未出现低频摆动的32.4%叶片中29.7%由静态渐变成上卷稳定，加上通过低频摆动过渡到上卷稳定的62.2%的叶片，叶片出现第二临界状态的概率为91.9%.未出现上卷稳定的8.1%的树叶随着风速的增大，由低频摆动转变为高频摆动，加上74.3%由稳定上卷突变到高频振动的叶片，出现高频振动的概率为82.4%.不存在高频振动的18.9%通过静态变化过渡到喇叭状稳定，存在高频振动的68.9%的叶片由高频振动突变到喇叭状稳定，喇叭状稳定存在的概率为87.8%，最终处于喇叭状稳定下的53.4%的树叶一直保持稳定直到实验的最高风速. 同样通过表1我们也可以分析得出叶片角在120°～160°区间内的树叶，随着风速变化所经历状态的改变及所占比例.从上表我们可以看出叶片角对各个临界状态所存在的比例均有影响，叶片角越小树叶处于振动状态的概率越高,叶片角越大叶片各个稳定的状态存在的概率就越高.这一特性在叶片是否存在最终稳态时表现的最为明显.

实验中我们发现叶片角的大小除了影响树叶的临界状态存在的概率以外,还会对树叶的临界风速有影响.由于叶片角较小的树叶不存在中间的S形稳定状态所以在下面的对比分析中我们只考虑树叶树叶存在的5个临界状态，即低频摆动、两侧往中间包起稳定、高频振动、喇叭状稳定、完全失去平衡.并将其对应的5个临界风速分别记为V1、V2、V3、V4、和V5，通过整理分析得出如表2所示的风速.

从表2我们可以看出叶片角大的树叶的各个临界风速都比叶片角小的片叶要高，当风速较低时不同叶片角树叶的临界风速差别较小，当风速增大到一定程度时，叶片角较大的树叶的临界风速明显要高于叶片角小的树叶.即在相同风速下树叶叶片角越大，树叶抗风能力越好.通过综合上述的两个方面，我们发现在受风作用时叶片角大的树叶比叶片角小的树叶稳定.

表2 不同叶片角的银杏树叶各临界风速均值

2.3 叶片角对树叶阻力系数的影响

我们知道树叶在受风作用稳定时的阻力系数与树叶自身的大小、形状等因素有关.实验中所使用的叶片如图1所示，为了准确的测量叶片的面积分别量取银杏叶片3个位置的半径r1、r2、r3发现r1、r2、r3的值都相似，所以我们可以将银杏叶片的面积近视为以r1、r2、r3的平均值为半径，银杏叶片角θ为弧度的扇形的面积，可以根据公式求出：

通过对实验数据的分析处理，我们得到180片不同叶片角大小的银杏树叶的阻力系数随雷诺数的变化趋势.如图4所示我们通过分别取叶片角为180°、150°、120°的银杏叶片各5片，每组相同叶片角的叶片分别标记为1、2、3、4、5号叶片. 研究不同叶片角的叶片的阻力系数随着雷诺数增大的变化规律，通过整理得出图4(a)、(b)、(c)分别为叶片角120°、150°、180°的银杏叶片其阻力系数随雷诺数的增大而发生改变的变化并最终趋于稳定的趋势图.

我们发现叶片角为180°的叶片其稳定时的阻力系数在0.15左右，叶片角150°的树叶其稳定时的阻力系数在0.20左右，叶片角为120°的叶片其稳定时的阻力系数在0.29左右.(当叶片角小于120°时树叶存在稳态的概率很小，本文暂时不做分析).将银杏叶片按叶片角从120°～190°分成若干组，每组分别取多片叶片角相同的叶片并求出其最终稳定时阻力系数，整理得到如图4(d)所示的银杏叶片最终稳定时的阻力系数随叶片角度的变化规律.从中我们不难发现叶片稳定时的阻力系数随着叶片角的增大而减小，从而进一步的证明了树叶的叶片角越大树叶受风作用时越稳定.

图4 叶片角对阻力系数的影响Figure 4 Influence of lamina angle of ginkgo leaf on drag coefficient

为了进一步验证树叶的阻力系数与叶片角之间的关系，我们通过对人造树叶在只改变叶片角其他条件保持不变的情况下进行实验测量，实验得到的结果与真实树叶的情况一致.

2.4 凹痕对真实与模拟叶片振动变形和临界风速的影响

在自然情况下部分银杏树叶在其树叶扇形的中间区域存在长短不一的凹痕，通过实验我们发现树叶是否具有凹痕以及凹痕的长度对银杏树叶的风振状态和临界风速都有影响.

在影响树叶在风中振动状态方面我们发现，是否具有凹痕对叶片前四个临界状态的影响较小. 如图5所示我们将带凹痕与不带凹痕银杏叶片分成2组进行实验，记录下每组叶片其存在稳定状态的概率随其叶片角的变化。通过图5我们可以发现存在凹痕的树叶相比于完整的树叶在高风速下更容易发生变形重塑从而保持稳定，并且树叶叶片角越小，这种作用效果越明显.

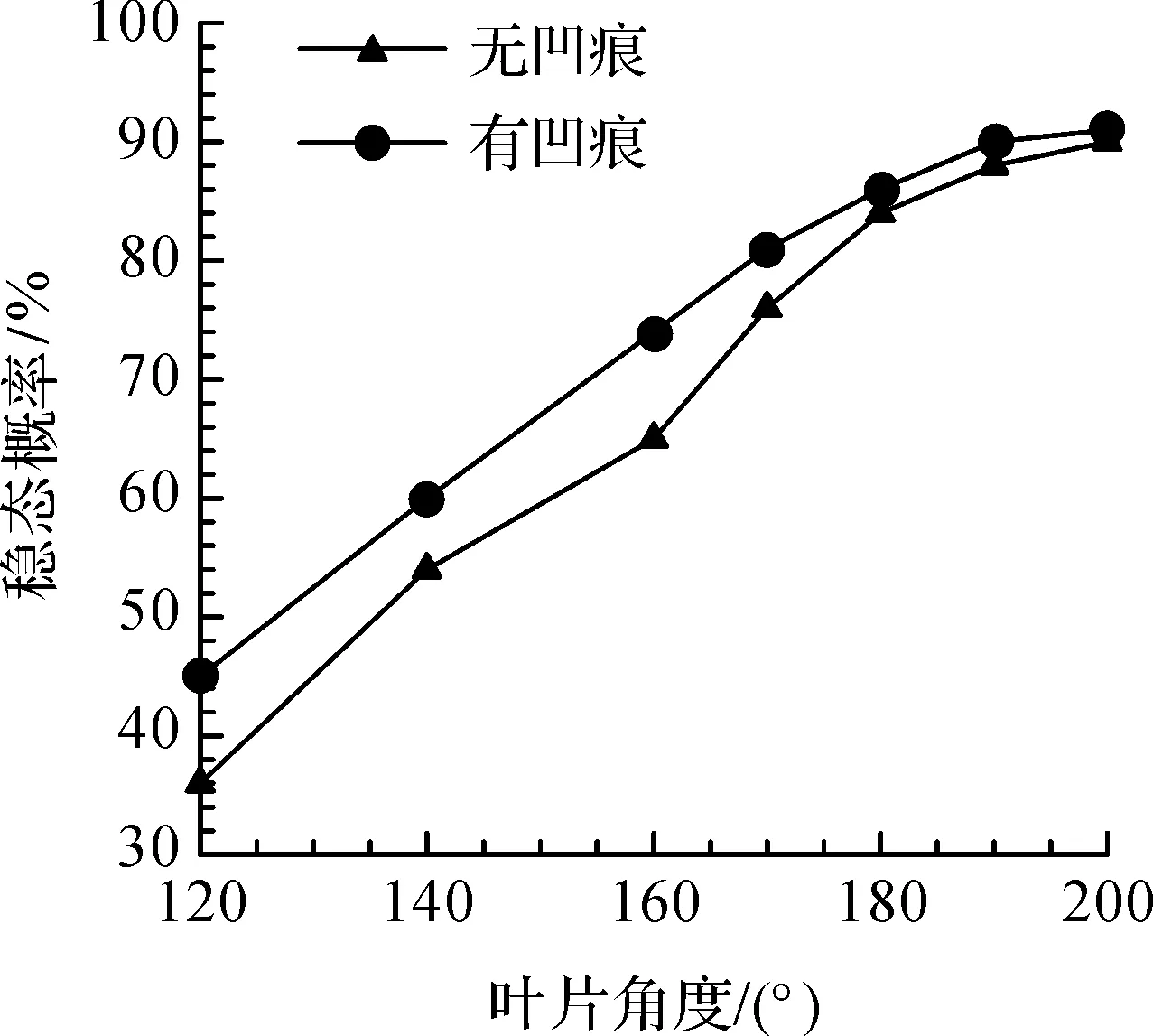
图5 凹痕对树叶稳态的影响Figure 5 Effect of indentation on leaf homeostasis

在测试叶片凹痕长度对树叶气动特性的影响时，我们希望通过人造树叶去模拟真实树叶在不同风速下的振动状态.这里我们取固定的叶片角为180°、叶柄长度为5 cm，宽度1.32 mm，厚度1.10 mm,半径为4.5 cm，叶片厚度为0.07 mm,的人造银杏树来进行实验分析.将实验中出现的六个临界状态：低频大幅整摆动，两侧叶片往中间合拢稳定，中频振动，S形稳定，高频振动，喇叭状稳定与之对应的六个临界风速，为了与前文出现的临界风速区分开这里我们分别记做V1、V2、V3、V4、V5、V6.

通过实验我们发现如表3所示规律,主要表现为当风速较小时，树叶处于第一和第二临界状态时，此时凹痕长度对树叶临界风速的影响较小，当风速增大到一定程度裂痕长度对临界风速的影响逐渐体现出来.树叶的临界风速随着凹痕长度的增加而减小，并在风速达到最高的第六临界状态时表现的最为明显.同时在实验中我们发现当叶片的凹痕长度超过自身半径的五分之三时，继续增加凹痕长度树叶将因为自身的结构被破坏从而无法形成稳态.

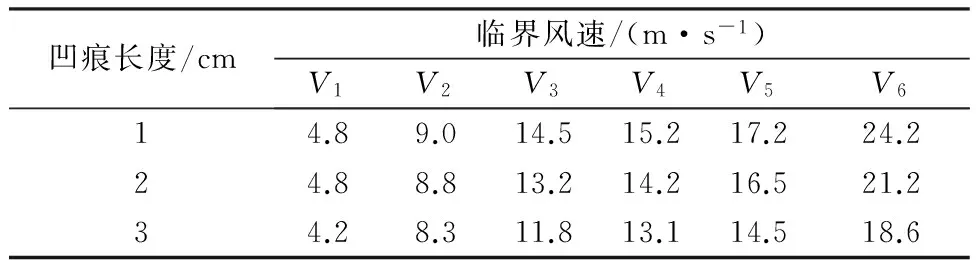
表3 凹痕长度对临界风速的影响

3 结 语

通过对实验结果的分析处理可以知道，银杏树叶在风洞中受风作用时其振动变形以及临界风速与树叶的叶片角存在紧密联系，叶片角越大树叶受风作用越容易发生结构重塑从而保持稳定，银杏树叶最终稳定时的阻力系数随着叶片角的增大而减小并最终稳定在0.15～0.30的范围内.凹痕长度不超过叶片半径的五分之三时，带有适当长度裂痕的叶片相比于完整的叶片更容易形成的稳态，当凹痕长度超过半径的五分之三时，叶片会因为整体结构遭到破坏而无法达到稳态.

[1] SHARIF, GENTRY T R, YEN J, et al. Transformative solar panels: a multidisciplinary approach[J].InternationalJournalofArchitecturalComputing, 2013, 11(2):227-246.

[2] 邵传平,朱园园. 鹅掌楸树叶在风中的变形与振动[J]. 力学学报，2017，49(2)：431-440.

SHAO C P, ZHU Y Y. The deformation and vibration of tulip leaves in wind[J].JournalofChineseTheoreticalandAppliedMechanics,2017,49(2):431-440.

[3] VOGLE S. Drag and reconfiguration of broad Leaves in high winds[J].JournalofExperimentalBotany, 1989, 40(8):941-948.

[4] 郑如侃. 梧桐树叶气动特性研究[D].杭州：中国计量大学,2016.

ZHENG R K.Researchontheaerodynamiccharacteristicsofplatanusacerifoliatreeleaves[D].Hanzhou:China Jiliang University，2016.

[5] TANEDA S. Waving motions of flags[J].JournalofthePhysicalSocietyofJapan, 2007, 24(2):392-401.

[6] SCHOUVEILER L, BOUDAOUD A. The rolling up of sheets in a steady flow[J].JournalofFluidMechanics, 2006, 563:71-80.

[7] ALBENL S, SHELLEY M, ZHANG J. Drag reduction through self-similar bending of a flexible body[J].Nature, 2002, 420(6915):479-81.

[8] 陈明,邵传平.杨树叶风振实验研究[J].中国计量学院学报,2014,25(1):63-69.

CHEN M, SHAO C P. Experimental investingation on the deformation and vibration of a poplar leaf in wind[J].JournalofChinaUniversityofMetrology,2014,25(1):63-69.

[9] SPECK O. Field measurements of wind speed and reconfiguration in Arundo donax (Poaceae) with estimates of drarces[J].AmericanJournalofBotany, 2003, 90(8):1253-1256.

[10] 朱园园,邵传平.鹅掌楸树叶气动特性研究[J].中国计量学院学报,2015,26(4):411-415,422.

ZHU Y Y, SHAO C P. Experimental investigation on the aerodynamic characteristics of liriodendron leaves[J].JournalofChinaUniversityofMetrology, 2015,26(4):411-415,422.