基于Laurent分解Multi-h CPM低复杂度解调方法*
2018-01-22崔中普窦高奇何铭嘉
崔中普, 窦高奇, 高 俊, 何铭嘉
(海军工程大学 电子工程学院,武汉 430033)
0 引 言
连续相位调制信号(CPM)是一类恒包络连续相位的调制信号。它具有很高的带宽和频率利用率。由于CPM的包络恒定,其对功放的非线性特性不敏感,因而功放可以一直工作在饱和状态;并且相位连续特性使得带外辐射较小,对邻道产生的干扰也较小,频谱效率高。而多指数连续相位调制(Multi-h CPM)具有若干个随着时间周期性变化的调制参数。它不仅具有一般CPM信号的优点,通过设置合适的调制指数,在提高了抗误码性能的同时,还可以实现使频谱更加紧凑、带外滚降速度更快以及更高带宽利用率的效果[1]。在带宽受限的情况下,与其他调制方式相比,Multi-h CPM有着更加优异的传输性能。在实际中,为了获得更高的功率和带宽效率,常常使用多进制以及较长关联长度,但其中任何一项的增大,都会使解调时状态数呈指数增长,大大增加了解调复杂度,限制了其在工程实际中的应用。
由于Multi-h CPM的优异性能,寻找实现其低复杂度解调方法的研究一直在进行。其中包括:最大似然序列检测(MLSD)的改进算法,改进型维特比译码算法等,虽然较传统MLSD有一定改善,但大量使用的匹配滤波器和网格状态仍限制其实际使用;信号空间映射,由于匹配滤波器的多少由传输信号空间的维数来确定,可以通过使用维数较低的子空间来代替原始信号空间的方法降低匹配滤波器的数目,缺点是网格状态数目并没有减少;信号的分解,主要包括PAM分解等。这些思想都是从牺牲解调性能来换取低复杂度的角度出发的。笔者主要在文献[2]的基础上,通过研究两种典型的Laurent分解,给出通用的分解形式,并采用计算机MATLAB仿真在冲击脉冲噪声信道下该解调方法的误码率性能,并与最基本的MLSD检测算法进行比较,分析性能的下降程度与解调复杂度的改善情况,为后续Multi-h CPM信号Laurent分解的DSP实现提供指导。
1 Multi-h CPM的信号模型
Multi-h CPM信号的复包络形式表示如下:
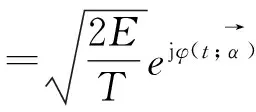
(1)
其中
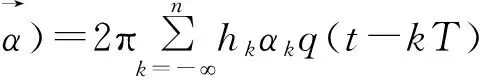
(2)
hk为调制指数,T为码元周期,αk为M进制的码元序列,αk∈{±2,±4,…,±M}。调制指数hk在每个码元周期内保持不变,若干个调制指数[h1,h2,…,hk]以周期K循环变化。q(t)为相位响应函数,与频率响应函数f(t)的关系为
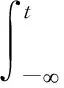
(3)
频率响应函数f(t)是一个持续时间为(0,LT)并满足以下条件的时限函数:
f(t)=f(LT-t)
(4)
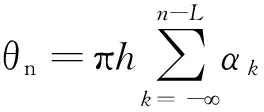
2 Multi-h CPM信号Laurent分解
2.1 Laurent分解过程
文献[3]中描述到:任何一个M进制恒幅相位调制信号均可以表示成一系列数目有限、时限的幅度调制脉冲(AMP)叠加的形式。这种思想带来的就是可以考虑将Multi-h CPM信号通过理论推导,分解成一系列线性PAM信号的叠加。这些脉冲信号能量并不均等,其中,少部分脉冲信号占据了大部分(98%左右)的能量,这样就可以仅用这几个波形来近似原始信号进行匹配[3],从而减少运算量。M进制Multi-h CPM信号可以分解为如下线性表示 :
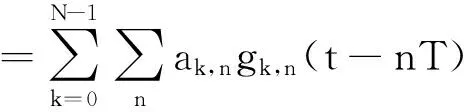
(5)
其中
N=QP(2P-1)(P=log2M,Q=2L-1)
(6)
表示分解后得到的脉冲个数,L为关联长度。
M进制数据序列αn∈{±1,±3,...,±(M-1)}可以表示为二进制系数集合的形式:
(7)
其中,ak,n和gk,n(t)为主要参量。系数ak,n称为伪符号,与发送数据有关,可表示如下:
(8)
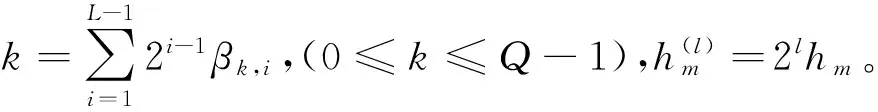
信号脉冲gk,n(t)可表示为
(9)
其中:
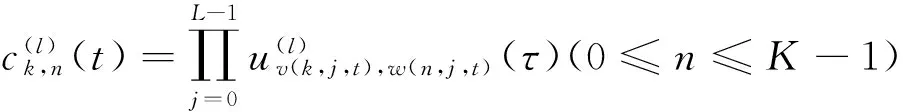
(10)
其中:
(11)
具体更加细致的推导过程可参考文献[4-5]。
Laurent分解具有如下的性质:
(1) 伪符号ak,n与信息数据是非线性关系,虽然s(t;α)线性地取决于伪符号ak,n,但它却是信息数据的非线性函数。这也是CPM调制非线性本质的体现。
(2) 相比于全响应系统(L=1),部分响应系统(L>1)存在更多的PAM波形。但通常情况下,信号能量都集中在第一个PAM波形中,而且波形均为时限的。
(3) 总体上来看,伪符号ak,n之间是相关的。
2.2 具体信号的Laurent分解
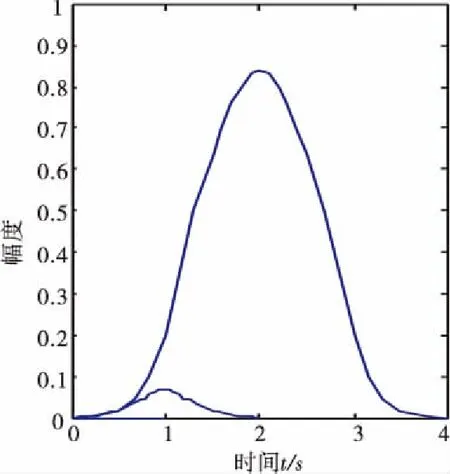
首先对具体信号进行Laurent分解,分析其能量分布情况。仿真采用的Multi-h CPM信号参数M=2,h={6/15,7/15}。具体结果如图1所示。
(a)奇数时刻
(b)偶数时刻图1 二进制Multi-h CPM信号的Laurent分解Fig.1 Laurent decomposition of binary Multi-hCPM signal
如图1所示,二进制多指数CPM信号,在奇数时刻和偶数时刻,各自可以分解为4个PAM脉冲。并且可以很明显地看到,信号的能量主要集中在主脉冲,约占总能量的98.2%,而其他3个脉冲能量迅速衰减。在进行后续匹配滤波时,可以考虑将主脉冲外的信号看做是干扰信息,用主脉冲来近似原始信号,将有效减少匹配滤波器的个数。
3 基于Laurent分解的最优化接收机
接收信号的基带复包络信号模[6-7]型为
r(t)=s(t;α)+n(t)
(12)
其中s(t;α)为发送信号,n(t)是零均值、双边功率谱密度为N0/2的加性高斯白噪声。由于s(t;α)是恒包络的,因而在接收时,最大似然与最大化相关是等价的。

(13)
将r(t)带入可得递归路径度量表达式为
(14)
zk,(n)对应于第n个码元中第k个匹配滤波器的输出。因为max{Dk}=L+1,min{Dk}=1,因此在实际处理中,通常有一个L符号的延迟。
根据以上的分析,得到了基于Laurent分解的最优化接收机框图如图2所示。匹配滤波器的个数与Laurent分解得到的PAM脉冲一一对应并且个数相同,均为N=QP(2P-1)。而次优接收机是将相似分解脉冲合并,仅需要M-1个匹配滤波器。匹配滤波器数目减少,运算量也随之减小,因而复杂度大大降低。

图2 基于Laurent分解的最优化接收机框图Fig.2 Optimal receiver block diagram based onLaurent decomposition
4 性能仿真分析
主要尝试对进制数M=2和M= 4两种Multi-h CPM信号的解调进行误码率仿真。将Laurent分解的最优和次优两种情况与最大似然序列检测算法进行比较[8],分析性能下降在可接受的范围内,解调的复杂度有多大程度的改善[9]。
图3为M=2,h={6/15,7/15}参数下的多指数CPM信号的Laurent分解解调的误码率曲线。分析可得:MLSD作为最优的解调方法,有着最好的误码率性能,但解调的复杂度也是最高的,需要30个匹配滤波器和一个60个状态的网格图。而采用基于Laurent分解的最优接收机仅需要4个匹配滤波器和一个60个状态的网格图。所需匹配滤波器的数目大幅度减少,但误码率性能却几乎没有下降。采用次优接收机,用第一个PAM脉冲来近似原信号,所需匹配滤波器的数目变成1个而网格状态数也减少为15个,性能的下降只有约0.4 dB,这是在可接受范围之内的。表1为M=2时,各算法复杂度比较。
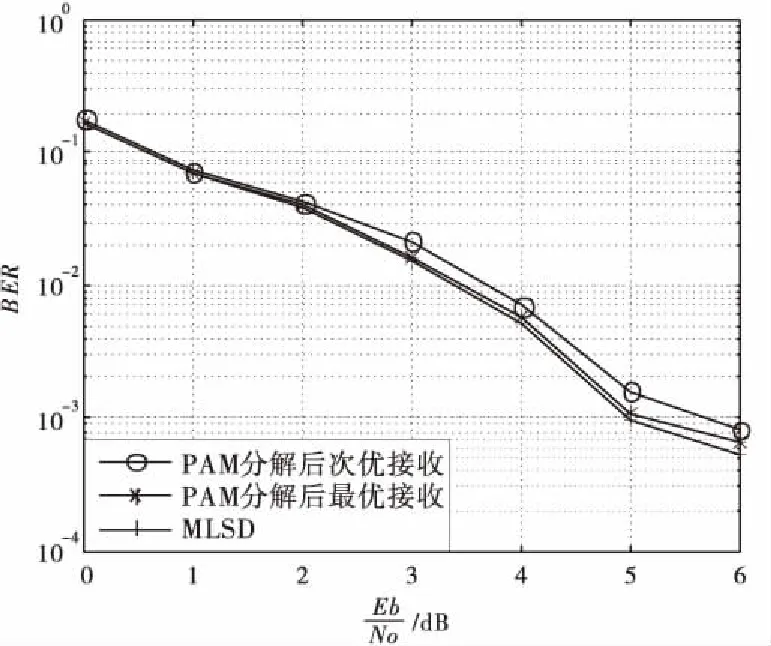
图3 M=2的Multi-h CPM基于Laurent分解的误码性能Fig.3 The error performance of M=2 Multi-hCPM based on Laurent decomposition
图4为M=4,H={4/16,5/16}参数下的多指数CPM信号的Laurent分解解调的误码率曲线。同上面分析一致,MLSD算法有着最好的性能但也对应着最大的解调复杂度,接收端需要128个匹配滤波器和一个256个状态的网格图。而采用基于Laurent分解的最优接收机仅需要48个匹配滤波器和一个256个状态的网格图,两者有着几乎一致的误码率性能,匹配滤波器的数目却大幅下降。次优接收机更是进一步减少了匹配滤波器的数目以及网格图状态数,对应性能损失约为1.8 dB。在考虑解调复杂度降低程度上,这样的性能损失也是可以接受的。表2为M=4时,各算法复杂度比较。
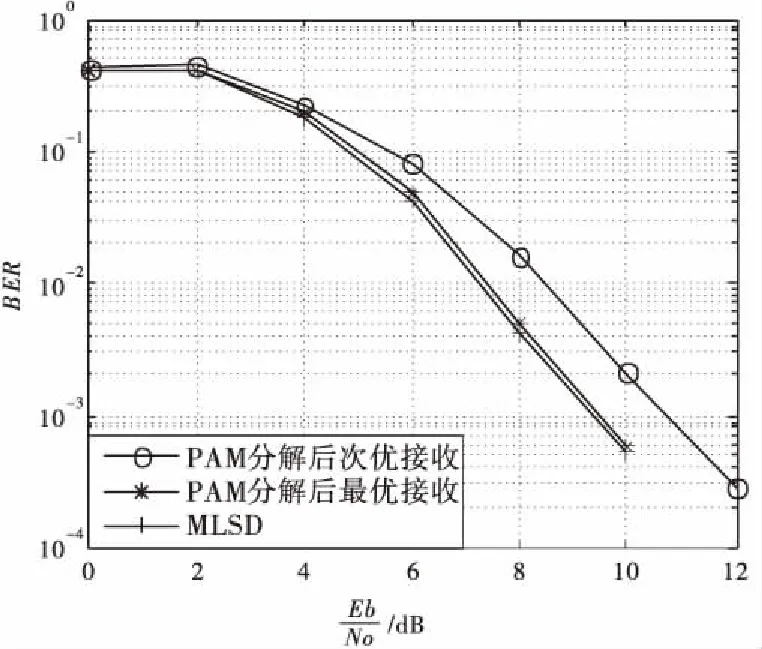
图4 M=4的Multi-h CPM基于Laurent分解的误码性能Fig.4 The error performance of M=4 Multi-hCPM based on Laurent decomposition表1 各种解调算法复杂度比较(M=2)Table 1 Complexity comparison of various demodulationalgorithms (M=2)

算 法匹配滤波器网格状态性能损失MLSD30600dBPAM最优460约0dBPAM次优1150.4dB
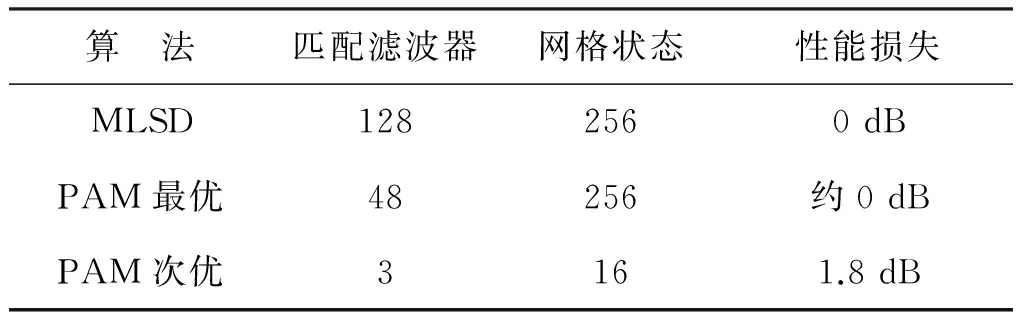
表2 各种解调算法复杂度比较(M=4)Table2 Complexity comparison of various demodulationalgorithms (M=4)
由仿真结果可以看出,误码率性能下降在可接受范围内,采用Laurent分解的Multi-h CPM信号解调复杂度有着明显的降低。
5 结束语
主要通过Laurent分解来寻求一种Multi-h CPM信号的低复杂度解调方法。采用把原信号表示成一系列PAM脉冲叠加的形式,用其中占据绝大部分能量的若干主脉冲来近似原始信号进行匹配滤波。仿真结果显示,这样做能有效减少解调过程中所需的匹配滤波器个数和状态网格图状态数,而性能的下降也只有0.4 dB和1.8 dB。CPM信号作为串行级联连续相位调制(SCCPM)的内码[10],通过对其低复杂度解调方法的研究来探索SCCPM的低复杂度实现方法,这也是后续研究工作的重点。
[1] PERRINS E,RICE M.Reduced-Complexity Detectors for Multi-h CPM in Aeronautocal Telemetry[J].IEEE Transactions on Aeropace and Electronic Systems,2007,43(1):286-300
[2] 钟凯,葛林东,巩克现.基于Laurent分解的多指数CPM低复杂度序列检测算法[J].信号处理,2011,27(5):717-720
ZHONG K,GE L D,GONG K X.A Low Complexity Sequence Detection Algorithm for Multi-h CPM Based on Laurent Decomposition [J].Signal Processing,2011,27 (5): 717-720
[3] MENGALI U,MORELLI M.Decomposition of M-ary CPM Signals into PAM Waveforms[J].IEEE Transactions on Information Theory,1995,41(5):1265-1275
[4] CARIOLARO G.A System-theory Approach to Decompose CPM Signals into PAM Waveforms[J].IEEE Transactions on Communications,2010,58(1):200-210
[5] LAURENT P A.Exact and Approximate Construction of Digital Phase Modulations by Superposition of Amplitude-modulaed-pulses(AMP)[J].IEEE Transactions on Communications,1986,34(2):150-16
[6] 温雄峰.CPM降低复杂度相干解调的性能研究[D].西安:西安电子科技大学,2013
WEN X F.The Study on Performance of Complexity Reduction of CPM Coherent Demodulation[D].Xian: Xian Electronic and Science University,2013
[7] 童启森,杜欣军.一种低复杂度的连续相位调制序列检测接收机[J].信息与电子工程,2009,7(6):529-532
TONG Q S,DU X J.A Low-Complexity CPM Sequence Detection Receiver[J].Information and Electronic Engineering,2009,7(6): 529-532
[8] 朱宏权,吴岭,游莎莎,等,Multi-h CPM体制误码和频谱性能分析[J].飞行器测控学报,2010,29(5):56-59
ZHU H Q,WU L,YOU S S,et al.BER and Spectrum Performance Analysis of Multi-h CPM System[J].Flight Vehicle Control,2010,29 (5): 56-59
[9] 门兰宁,葛持恒.通信系统中Viterbi译码的MATLAB仿真与实现[J].电子科技,2012,25[3]:34-37
MEN L N,GE C H.The MATLAB Simulation of Viterbi Decoding in Communication System[J].Electronic Tech-nology,2012,25[3]: 34-37
[10] 赵连杰.串行级联CPM系统的迭代译码研究[D].大连:大连理工大学,2007
ZHAO L J.Research on Iterative Decoding of SCCPM Systems [D].Dalian: Dalian University of Technology,2007
