应用超宽带特征基函数法快速计算目标宽带RCS*

汪 强， 王仲根， 张永刚

(安徽理工大学 电气与信息工程学院，安徽 淮南 232001)

0 引 言

目标宽带雷达散射截面(RCS)的精确预估对于高分辨率雷达成像技术、反隐身技术以及目标识别的研究具有重要意义。传统矩量法(MoM)[1]在计算目标宽带RCS时，需要对频带内所有频率点逐一计算，计算十分耗时。随着一些高效MOM，如快速多极子法(FMM)[2-3]、多层快速多极子法(MLFMM)[4-5]、自适应积分法(AIM)[6-7]、特征基函数法(CBFM)[8-9]等被相继提出，极大地提高了MOM在单频点处的计算效率，但在求解目标宽带、超宽带RCS时，若目标在待求频段内特性变化频繁，为达到理想的计算效果，就必须增加采样频率点的个数，新增频率点阻抗矩阵的构造与求解将会增加计算量。因此，在待求频段内如何运用尽可能少的采样频点信息来得到整个频段内的RCS将显得十分必要。为此，许多有效的方法被相继提出，文献[10]提出了利用MLFMM与阻抗插值技术相结合的方法来计算目标宽带RCS；文献[11]应用MLFMM结合最佳一致逼近来加快目标宽带RCS计算，但上述方法在求解线性方程组时均采用迭代法求解，收敛速度缓慢。渐近波形估计(AWE)[12]技术被学者用来求解目标宽带RCS并取得了较好的效果[13-14]，但技术在求解过程中占用了大量的内存来储存稠密矩阵以及频率导数矩阵，加大了内存需求。文献[15]提出一种AWE技术结合CBFM求解目标宽带RCS的方法；文献[16]提出一种自适应CBFM与模型参数估计技术相结合的方法来计算目标宽带RCS，虽然上述两种方法利用CBFM加快了插值点电流的求解速度，减少了内存消耗，但每个插值点的特征基函数(CBFs)仍然需要重新求解。最近国外学者M.D.Gregorio提出一种超宽带特征基函数法(UCBFM)[17]分析目标宽带电磁散射特性，方法首先在待求频带的最高频率点建模，采用多角度平面波激励照射各个子域，求解出各个子域的主要特征基函数(PCBFs)后，再经过奇异值分解(SVD)得到超宽带特征基函数(UCBFs)，UCBFs可表达出较宽频段内的电流特性，故可以在待求频段内复用，无需再逐一计算每个频点的CBFs，计算效率显著提高。但在求解低频率点的RCS时，应用UCBFs虽然不必重新计算每个频率点的CBFs，但是待求频点处的缩减矩阵需重新构造，仍要耗费大量计算时间。

为避免各频率点处缩减矩阵的重新构造，将UCBFM与最佳一致逼近结合，首先求解出待求带宽内的各切比雪夫节点；其次应用UCBFM计算出各节点处的目标表面电流，每个节点的CBFs无需重新求解，直接应用UCBFs即可；最后应用最佳一致逼近技术获得任意频点处目标表面的电流信息，从而得到目标在整个宽带的RCS。数值计算结果表明，方法和传统UCBFM相比，计算效率显著提高。

1 超宽带特征基函数法

(1)

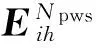
(2)

ZR(f)·α(f)=VR(f)

(3)

(4)

式(4)中，Zij(f)为互阻抗矩阵。由于ZR(f)维数较小，α(f)可以直接由式(3)求解得到，再将α(f)代入式(2)，即可获得目标在任意频率f处的表面电流。虽然UCBFs能够在每个频点复用，但当频率f变化时，子域间阻抗矩阵Zij(f)需要重新计算，ZR(f)也需重新构造。由式(4)可知，ZR(f)的构造过程中存在复杂的矩阵向量积运算，对每个频率点重新构造ZR(f)将不可取。

2 最佳一致逼近

为快速获得目标宽带RCS，将UCBFM与最佳一致逼近相结合(UCBFM-Chebyshev)，首先应用UCBFM求解出目标在各切比雪夫节点位置的电流，然后应用最佳一致逼近得到待求频带内任意频点的表面电流，由此实现快速求解目标宽带RCS的目的。具体实现过程如下：

(1) 对于给定频带f∈[fa，fb]，对应的波数k∈[ka，kb]，利用坐标变换得：

(5)

(2) 在[ka，kb]中确定n个切比雪夫节点，其表达式为

(6)

(7)

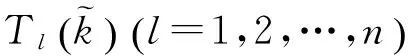
(8)

(9)

(3) 根据最佳一致逼近理论，目标表面电流I(k)可表示为

≈

(10)

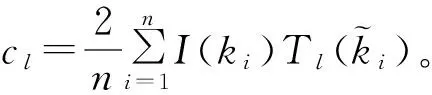
从式(10)可以看出，仅需应用UCBFM求解出n个切比雪夫节点ki处的电流I(ki)，再通过求解式(10)便可得到目标在整个宽带内任意频点的电流，从而快速获得目标宽带RCS。

3 数值算例与结果

为了验证方法的有效性与精准性，分别求解了一个组合导体与一个杏仁导体的宽带RCS，SVD门限取0.001。

算例1：计算了一个组合体导体在0.5～3 GHz的宽带RCS，组合体顶部宽0.15 m，疷部宽0.075 m，高0.25 m，入射角=0°，φ=0°。在3 GHz建模，目标表面经三角单元剖分后，得到2 326个三角单元，5 084个未知变量，沿z轴将其划分4为个子域。分别使用UCBFM、UCBFM-Chebyshev来计算目标的宽带RCS。两种方法均在θ与φ两个方向分别设置20个激励，SVD去除冗余后，每个子域获得146个UCBFs。

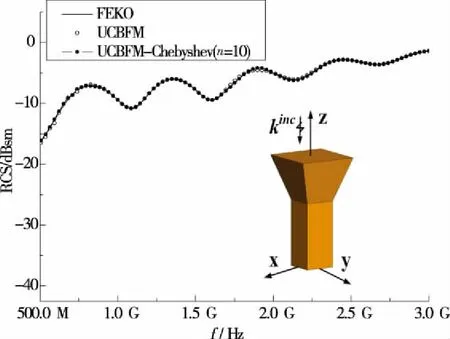
图1 组合体宽带RCSFig.1 The wide-band RCS of combination

图2 杏仁体宽带RCSFig.2 The wide-band RCS of NASA almond

应用UCBFM逐点求解目标在0.5～3 GHz的宽带RCS，计算步长为25 MHz；运用UCBFM-Chebyshev只需计算10个切比雪夫节点的电流，即可得到目标整个宽带RCS。图1分别给出了两种方法的计算结果，从图1中可以看出UCBFM-Chebyshev与UCBFM吻合较好，具有较高的计算精度。

算例2：求解了一个252.374 4 mm杏仁导体的宽带RCS，激励波入射角度θ=0°，φ=0°，频宽为0.5～3 GHz。在3 GHz建模，目标表面经三角单元剖分后，得到2 654个三角单元，5 752个未知量，沿x轴将其划分为4个子域。两种方法在θ与φ两个方向均设置20个激励，每个子域获得121个UCBFs。应用UCBFM逐点求解目标宽带RCS，计算步长为25 MHz；而应用UCBFM-Chebyshev，只需求出9个切比雪夫节点处目标表面电流即可得到整个目标宽带RCS。两种方法的计算结果如图2所示，从图2可以看出UCBFM-Chebyshev与商业软件FEKO、UCBFM的计算结果吻合较好。

表1给出了两种方法的计算时间，从表1可以看出，在保证精度的情况下，相比于UCBFM，UCBFM-Chebyshev具有更高的计算效率。

表1 两种方法计算时间Table 1 The calculation time of the two methods

4 结 论

提出了一种UCBFM结合最佳一致逼近快速求解目标宽带RCS的方法，方法充分利用了最佳一致逼近技术的优点，只需求解各切比雪夫节点的电流，便可快速得到待求频段内任意频点的表面电流，避免了对每个频率点缩减矩阵重复构造，达到快速求解目标宽带RCS的目的。计算结果表明，方法与传统超宽带特征基函数法相比，具有更高的计算效率。

[1] HARRINGTON R F.Field Computation by Moment Method[M].New York： Macmillan，1968

[2] COIFMAN R，ROKHLIN V，WANDZURA S.The Fast Multipole Method for the Wave Equation： A Pedestrian Prescription[J].IEEE Transactions on Antennas and Propagation，1993，53(3)： 7-12

[3] 丁振宇，洪伟.快速多极子在任意截面均匀介质柱散射中的应用[J].电波科学学报，2001，16(3)： 283-286

DING Z Y，HONG W.Application of FMM to Electromagnetic Scattering from a Homogeneous Cylinder of Arbitrary Cross Section[J].Chinese Journal of Radio Science ，2001，16(3)：283-286

[4] SONG J M，LU C C，CHEW W C.Multilevel Fast Multipole Algorithm for Electromagnetic Scattering by Large Complex Objects [J].IEEE Transactions on Antennas and Propaga-tion，1997，45(10)： 1488-1493

[5] 王元源，谢拥军，王鹏.电大尺寸辐射问题的预修正多层快速多极子分析 [J].西安电子科技大学学报，2007，37(3)： 596-599

WANG Y Y，XIE Y J ，WANG P.Analysis of the Electrical Large Radiation Problem with the Pre-corrected Multilevel Fast Multipole Algorithm [J].Journal of Xidian University(Natural Science Edition)，2007，37(3)：596-599

[6] 黄春明，安翔，吕志清.电大尺寸线面结构辐射特性的自适应积分方法准确分析 [J].西安电子科技大学学报(自然科学版)，2009，36(4)： 721-724

HUANG C M，AN X，LV Z Q.Accurate Analysis of Electrically Large Wire-to-surface Configurations by the Adaptive Integral Method [J].Journal of Xidian University(Natural Science Edition)，2009，36(4)： 721-724

[7] 马骥，龚书喜，王兴，等.一种快速计算目标宽带雷达散射截面的电磁算法 [J].西安电子科技大学学报(自然科学版)，2012，39(4)： 124-129

MA J，GONG S X，WANG X，et al.Fast Computation of the Wide-band Radar Cross Section of Arbitrary Objects[J].Journal of Xidian University(Natural Science Edition)，2012，39(4)： 124-129

[8] 孙玉发，卢克，王国华.介质目标电磁散射特性的多层特征基函数法分析 [J].电波科学学报，2013，28(1)： 92-96

SUN Y F，LU K，WANG G H.Analysis of Electromagnetic Scattering Characteristics from Dielectric Objects Using Multilevel Characteristic Basis Function Method [J].Chinese Journal of Radio Science，2013，28(1)：92-96

[9] 王国华，孙玉发，于君之.特征基函数法快速分析导体目标电磁散射特性[J].电波科学学报，2013，28(3)： 438-442

WANG G H，SUN Y F，YU J Z.Fast Analysis on Electromagnetic Scattering Characteristics of Conducting Targets Using Characteristic Basis Function Method[J].Chinese Journal of Radio Science，2013，28(3)：438-442

[10] FAN Z H，LIU Z W，DING D Z，et al.Preconditioning Matrix Interpolation Technique for Fast Analysis of Scattering Over Broad Frequency Band [J].IEEE Transac-tions on Antennas and Propagation，2010，58(7)： 2484-2487

[11] 田超，谢拥军，王元源，等.MLFMA结合最佳一致逼近快速求解目标宽带RCS [J].电子与信息学报，2009，31(11)： 2772-2775

TIAN C，XIE Y J，WANG Y Y，et al.Fast Solutions of Wide-band RCS Pattern of Objects Using MLFMA with the Best Uniform Approximation [J].Journal of Electronics and Information Technology，2009，31(11)： 2772-2775

[12] REDDY C J，DESHPANDE M D，COCKRELL C R,et al.Fast RCS Computation Over a Frequency Band Using Method of Moments in Conjunction with Asymptotic Evaluation Technique [J].IEEE Transactions on Anten-nas and Propagation，1998，46(8)： 1229-1233

[13] WANG X，GONG S X，GUO J L，et al.Fast and Accurate Wide-band Analysis of Antennas Mounted on Conducting Platform Using AIM and Asymptotic Waveform Evaluation Technique [J].IEEE Transactions on Antennas and Propagation，2011，59(12)： 4624-4633

[14] SUN Y F，XU S J.Fast Computation of Wide-band Radar Cross Section Using Asymptotic Waveform Evaluation Technique [J].Journal of Infrared and Millimeter Waves，2002，21(6)： 469-472

[15] SUN Y F，DU Y，SAO Y.Fast Computation of Wide-band RCS Using Characteristic Basis Function Method and Asymptotic Waveform Evaluation Technique [J].Journal of Electronics，2010，27(4)： 463-467

[16] 韩国栋，潘宇虎，何丙发，等.AMCBFM-MBPE快速分析三维目标的宽带宽角散射特性 [J].微波学报，2009，25(6)： 32-37

HAN G D，PAN Y H ，HE B F，et al.Fast Analysis for 3-D Wide-band & Wide Angle Electromagnetic Scattering Characteristic by AMCBFM-MBPE [J].Journal of Micro-waves，2009，25(6)： 32-37

[17] DEGIORGI M，TIBERI G，MONORCHIO A.Solution of Wide Band Scattering Problems Using the Characteristic Basis Function Method [J].IET Microwaves Antennas & Propagation，2012，6(1)： 60-66