悬挂式单轨车制动盘摩擦仿真分析

徐 焱 张卫华王月明

（1.西南交通大学牵引动力国家重点实验室，610031，成都；2.西南交通大学机械工程学院，610031，成都∥第一作者，博士研究生）

悬挂式单轨车是城市轨道交通车辆类型中的一种重要型式。其特点在于其轨道为特殊形状的箱型梁，梁体一般为空心向下开口，且车辆悬挂于轨道下方运行。悬挂式单轨车运行时转向架处于轨道梁内部，而车体悬挂于下方，由悬挂装置与转向架连接。悬挂式单轨车的制动方式一般有2种：①转向架上的制动板与轨道梁的摩擦制动；②转向架的走行轮上带有的制动闸片进行的闸瓦制动。目前，国外以日本千叶县0系为首的大部分悬挂式单轨车均采用制动盘制动。闸瓦制动时，由于闸瓦温度急剧升高以及热应力的不均匀分布而产生的热裂纹，是致使闸片失效的重要因素。因此，研究制动闸片制动时的温度场和应力场具有重要的意义。本文通过有限元法对悬挂式单轨车正常制动时闸片的温度场和应力场进行了仿真，重点研究了闸片的热功率转换情况，为未来中国引进悬挂式单轨车时闸片的设计优化提供理论参考。

1 制动盘热分析

过去进行制动盘温度场和热应力场分析主要采用热功率法。该方法的核心在于将车辆动能的90%转换为摩擦产生的热能，再将热能转换为随时间变化的热流密度。起初研究者将整个摩擦盘简化为二维模型，忽略了如散热筋、螺纹装配孔等特征的影响，这样得到的仿真结果无法完整地体现整个制动过程，尤其无法判断散热筋等特征的热影响［1］。此后的研究者采用完整的三维模型进行仿真，但又简单地认为热密度是严格按时间递减的函数［2］，未考虑到制动初始状态时由于制动压力递增造成的热密度递增的情况。此外，由于制动盘与周围空气存在热交换，故应考虑热交换的情况。热交换包括热传导、热对流和热辐射。其中，热传导主要为制动摩擦块与制动盘之间的传导，而制动盘与轴之间的热传导可忽略不计。

1.1 热流计算

制动盘的热载荷即输入热流密度，其主要加载于制动盘的摩擦面上。本文采用改进的热功率法进行热流计算。该方法认为：加载于制动盘上的全部热量即为绝大部分的列车动能。热流密度分2个阶段加载：第1阶段从开始制动到制动摩擦闸片压力达到最大，第2阶段从制动摩擦闸片压力最大到列车停止前进。整个制动过程的全部输入热量Q总表示如下［3］：

式中：

M——轴重；

v0——开始制动时列车运行速度；

μ——功热转换参数，综合考虑悬挂式单轨车的运行情况，该参数取0.85。

对于第1阶段加载情况，悬挂式单轨车制动摩擦闸片的压力大约在2 s内就快速上升到最大值，即：

式中：

P——摩擦闸片受到的压力；

k——管道气压衰减系数；

t——制动时间。

作用于摩擦闸片的单位面积摩擦力矩为：

式中：

Δs——摩擦闸片的单位面积；

μ0——制动摩擦系数（该值可假定为常数）；

Δθ——摩擦闸片的单位角度；

r——摩擦闸片的的半径；

Δr——摩擦闸片的单位面积所对应的半径。

则单位时间内单位面积摩擦力所做的功为：

式中：

ω——制动盘转动角速度；

Δt——单位时间。

摩擦力所做的功可认为按功热转换系数转化为摩擦盘所受的热，故有：

式中：

ΔQ——摩擦力所做的功。

因此，单位时间内总摩擦功为：

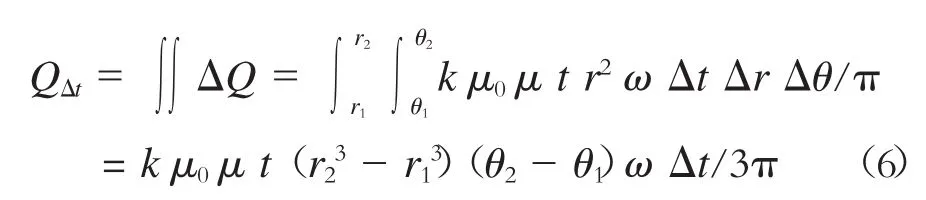
式中：

r1，r2——摩擦块对应的内径和外径；

θ1，θ2——摩擦块对应的始角和终角。

综上，根据热流密度的定义可得热流密度q（t）为：

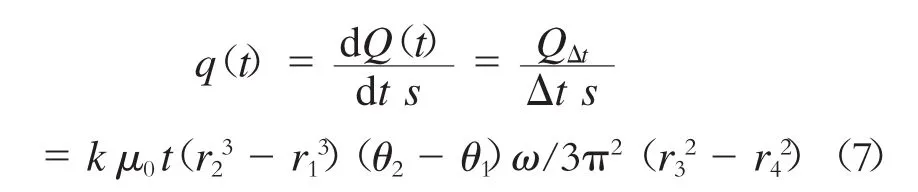
式中：

Q（t）——摩擦热量；

r3——制动盘摩擦面的外径；

r4——制动盘摩擦面的内径；

s——制动盘的摩擦面积。

对于第2阶段加载情况，由于制动压力保持最大，所以制动摩擦力不变，因此可采用基本功热转换法计算这一阶段的热流密度。Q（t）可表示如下［4］：

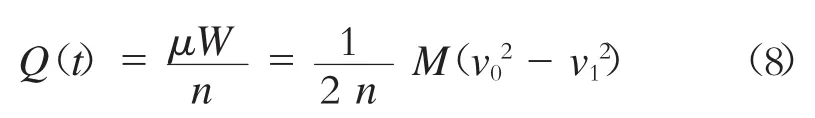
式中：

W——制动盘的热功率；

n——车轴上参加制动的制动盘数目，对于日本千叶线0系车，该值取2；

v1——t时刻列车的运行速度。

因此第2阶段的热流密度随时间变化的函数为：

式中：

a——制动减速度。

1.2 对流换热系数

悬挂式单轨车制动盘及其所处的环境为半封闭式的轨道梁。因此，其与空气的热对流情况与一般的城市轨道交通车辆有较大区别。理论上对流换热系数与材料无关，仅取决于流体的流动状态、流体的物理性质、壁面温度以及壁面的几何形状。对于半封闭式的轨道梁内部高速运行的转向架，可认为其处于一种管道内的强迫对流传热状态。假定制动闸片为热交换管面，则制动闸片上的热交换系数为［5］：

式中：

λ——空气导热系数；

Pr——普朗特数。

忽略制动盘温度变化对周围空气温度的影响，则ρ、μ1、Pr均为常数，α仅与v和d有关，而v则与空气流动速度v∞和制动盘线速度vr有关。制动盘盘面上的空气相对流动速度和制动盘侧面的空气相对流动速度不同。制动盘盘面上的v表示为：

对于制动盘的侧面，由于各部分间空气相对流动速度较小，因此制动盘侧面的空气相对流动速度可简化为列车运行速度。

1.3 热辐射系数

任何时刻物体均向外部产生热辐射，热辐射与物体和外部环境的温度差有关。为方便计算，将热辐射的Stefan-Boltzmann公式采用Newton冷却定律转换为对流散热的辐射换热系数αr［6］：

式中：

ε——辐射率，取值为0.21；

σ——斯蒂芬-玻尔兹曼常数，取值为5.67×10-8W/（m2·℃4）；

T——制动盘的边界温度，℃；

T0——环境温度，℃；本文将制动盘制动时的初始温度20℃作为环境温度。

1.4 离心力载荷

制动盘在制动工况中由于高速旋转，会产生一定的离心力F0：

式中：

Δm——制动盘上单位体积所对应的质量；

rF——制动盘单位体积所对应的半径。

由于ANSYS仿真分析中以角速度代表离心力，因此只需将角速度和制动盘密度加载即可。

2 制动盘温度场有限元仿真分析

采用ANSYS 12.0作为不同工况下瞬态温度的求解工具。建立一个统一的制动盘模型来同时计算热应力和结构应力。热应力与结构应力计算间不存在数据转换处理，可有效地提高计算速度和精度。

本文以日本千叶县的0系悬挂式单轨车为研究对象。该单轨车制动盘为简单的盘型结构，未设置散热筋等装置，制动盘装在走行轮上，由轮毂与之连接，用8个螺栓紧固。制动盘结构参数如表1所示。制动盘材料参数如表2所示。

表1 日本千叶县的0系悬挂式单轨车制动盘结构参数表m

表2 日本千叶县的0系悬挂式单轨车制动盘材料参数表

以悬挂式单轨车正常制动工况为仿真工况。该工况为悬挂式单轨车最为主要的制动工况，具有较大的研究意义。在仿真分析中,制动盘模型采用四面体soild 70单元，制动盘摩擦面采用surf 152单元，模型总共3 138个单元。制动盘有限元模型如图1所示。

图1 制动盘有限元模型

正常制动工况下，制动盘的制动初始速度为80 km/h，制动持续时间为18 s。通过计算分析可知，在16.4 s时制动盘摩擦面达到最大温度204.796℃，其温度分布如图2所示。

图2 制动盘正常制动工况下的温度分布

正常制动工况下，虽悬挂式单轨车的速度较低，但由于制动盘面积小、厚度小、摩擦面积大且制动盘无特殊的散热结构，加上制动时间短，因此制动盘的最高温度处于一个较高水平。此外，制动盘的摩擦面达到最高温度后下降，而盘内温度一直处于上升趋势。这是由于制动盘开始制动时其吸收的热量大于散发的热量，因而温度上升；但当速度较低时热量的输入值小于散发的热量，因而温度下降。而制动盘盘内一直处于吸收热量大于散发热量的状态，因此温度一直上升。制动盘盘面温度变化趋势如图3所示。

图3 制动盘盘面温度变化趋势图

3 制动盘热应力分析

悬挂式单轨车制动时，制动盘处于力和温度的共同作用下。制动盘在力场和温度场的共同作用下的有限元方程为：

式中：

K——总刚度矩阵；

δ——节点位移矩阵，即制动盘在机械载荷和热载荷共同作用下的结构变形矩阵。

RT——温度变化引起的载荷矩阵；

R——机械载荷（包括由于制动盘旋转产生的离心力、振动载荷、压力载荷等）矩阵。

为得到制动盘内部的应力分布和结构变形，需对模型进行结构分析。将soild 70单元转换为soild 45单元，且将计算得到的温度场作为载荷加载到制动盘上，同时施加离心力和位移载荷进行结构分析，求解得到制动盘最大等效应力分布，如图4所示。

图4 制动盘最大等效应力分布图

由图4可知，制动盘上的应力分布基本均匀，未出现大范围的应力突变，但最大应力出现在施加了z轴方向移动约束的螺纹孔处，而最小应力出现在摩擦面与非摩擦面的交接处。这是由于模型上同时施加了离心力载荷和热载荷，制动时离心力载荷使制动盘出现了由轴心向外侧扩散的变形，而施加在摩擦面上的热载荷又使得摩擦面出现了较大的膨胀变形，并使得变形向内部扩散，2个变形在交接处相互抵消，使得该处的应力最小；而由于制动盘内部在制动过程中温度基本保持了原始温度，未产生热膨胀变形，又因为此处有对变形的约束，在离心力载荷的约束下，该处的应力在螺纹孔内部达到最大值。制动盘在此制动工况下的径向变形情况如图5所示。

图5 制动盘径向变形图

由图5可知，制动盘的最大正向变形出现在摩擦面边缘，而最大反向变形出现在制动盘内圈边缘。这是由于作用在摩擦面的热载荷最大，因而造成的热膨胀变形最大。而制动盘内部在约束与离心力的共同作用下，出现了反向的最大位移，而在摩擦面与非摩擦面的交接处位移最小，同时亦验证了此处应力最小的结论。

另外，制动盘盘面局部最大径向变形达到了0.893 mm，而根据日本千叶县悬挂式单轨运营公司的标准，车辆制动时制动盘径向变形均值为0.516 mm。该变形虽可以满足制动性能的要求，但仍超出了该车型一般制动盘变形的均值水平。长期处于大变形状态可能造成制动盘性能下降，甚至产生裂纹和断裂。因此，在未来的研究中该问题应重点解决。

4 结语

为验证仿真结果，本文将ANSYS仿真结果与日本千叶县悬挂式单轨运营公司所进行的制动盘制动试验的结果进行对比。前者得到的制动盘盘面最大温度为204.796℃，最大热应力为0.377×1010Pa。后者得到的制动盘盘面最大温度为206.4℃，最大热应力为0.412×1010Pa。由此可以看出，本文的仿真结果与实际试验结果差别较小，具有一定的合理性。

综合制动盘的温度场、应力场以及径向变形的分析可知，制动盘在正常工况下可以满足性能需求，但由于结构过于简单，造成了结构局部区域变形较大的结果。同时，在制动盘盘边出现了0.893 mm的较大变形。如果长期出现这样的大变形，对于制动性能和使用寿命均有不利影响。因此，在引进悬挂式单轨车时需考虑此类情况，并在此基础上进行相应的优化设计。本文的分析结果可为今后制动盘的优化设计提供参考。

［1］ 丁群.提速客车制动盘温度场及应力场的有限元分析［D］.北京：北方交通大学，2001.

［2］ 陈德玲，张建武，周平.高速轮轨列车制动盘热应力有限元研究［J］.铁道学报,2006，28（2）：39.

［3］ 杨勇强，李小莹，曹博涛，等.湿式摩擦离合器摩擦片的热力耦合分析［J］.机械传动，2016，40（1）：153.

［4］ 张新芳，李芾，孙树磊，等.快速货车制动盘热应力分析［J］.铁道机车车辆，2012，32（4）：35.

［5］ 戴锅生.传热学［M］.北京：高等教育出版社，1999.

［6］ 魏涛.基于ANSYS的盘式制动器结构分析及振动噪声研究［D］.长春：吉林大学，2007.