一种针对雷达成像的时域线性采样优化方法∗
2018-01-21
(桂林电子科技大学信息与通信学院,广西桂林541004)
0 引言
在过去数十年中,随着应用于国防、救灾、医疗等领域的设备与相关技术的需求不断增强,实用性探测雷达成像技术得到一定的发展,一些针对回波数据逆问题求解的成像算法也应运而生。其中一类利用时域数据的重构算法,例如时延求和、时间反转镜等算法,由于具有较为直观的可视性、原理简单等特点,因此具有一定的研究价值,但是此类方法通常存在重复运算较多、分辨率较差、无法反映目标外形、重构结果存在多重解、数据容易受到复杂场景结构布局和杂波干扰等弊端。而在另一类利用频域数据的算法中,一种由Colton等提出的频域线性采样法(LSM)[1]得到了广泛的关注,该方法通过构造一个可以区分采样点是否属于散射体内部的指示函数,对回波数据进行逆问题求解,该方法可以在先验信息较少的情况下对散射目标进行成像重构,因此具有很高的实用价值。随后一系列基于该算法的改进方法得到了研究和验证。例如,Nakamura等利用LSM求解热导体边界逆问题[2];Audibert等提出一种利用LSM结合部分确知散射体外形特征的数学模型求解逆问题的方法[3];Bazán等提出一种改进的最大间距准则并结合LSM方法求解逆问题[4];Erramshetty等提出一种利用LSM求解混合边界特性散射体外形的方案[5]。尽管频域线性采样法有较好的边界重构效果,但相较于时域数据,频域数据运算通常只能针对单一频点或多频点分别运算后叠加,而待测场景整体信息分布在各个频点中,单独某个频点数据包含的信息分量较少,因此需要大量观测角度下的数据作为支撑。
针对传统时域数据的特点和频域方法的优势,已经出现了一些时域线性采样法(TD-LSM)求解逆问题的研究。例如,Aramini等提出一种利用单一功能化函数的傅里叶变换替代采样点的离散远场检验函数[6]。但是此方法本质是将时域信号转换为频域信号,利用主频点及其附近频点的频域数据进行单频点或多频点数据运算后叠加。Carayol等提出一种直接利用时域数据的TD-LSM方法[7]。Guo等给出了TD-LSM和多频点LSM方法在小孔径雷达、有限观测角度和不同数据支撑条件下的性能比较[8]。Khaji等提出一种在已知弹性边界数据条件下利用TD-LSM探测隐蔽空洞的方案[9]。Haddar等将时域线性采样扩展到求解满足罗宾纽曼边界条件的散射体问题上[10]。Chen等针对对称外形散射体提出一种半平面TD-LSM方法[11]。尽管TD-LSM数据中包含了较多的分量信息,且一定程度上避免了需要大量观测角度下的数据支撑。但由于TD-LSM需要将原始数据变换为离散卷积形式,导致运算消耗严重增加,且计算检验函数过程中的辐射时延没有特定的选取标准。
为了克服以上传统TD-LSM的缺陷,本文主要通过分析时域数据波场传播特性,利用信号互相关特性,首先提出并验证了最佳时延值选取准则,并进一步在基于最佳时延选取准则的基础上,提出一种基于分割思想的TD-LSM改进算法,该方法先利用各个发射阵元的零时信号与接收信号进行互相关运算,预先获得各道接收信号的时延值,再利用这些时延值求出该发射阵元到达散射体的平均时延,作为等式右侧最佳时延值,以此替代经验选取时延方法。随后,在每个采样点运算过程中根据该点到各个阵元走时范围,将等式左右两端的数据矩阵和计算点源辐射函数分割,截取其中有效数据后,再利用TD-LSM进行运算,以此提高运算效率。
1 线性采样法公式化分析
1.1 引入雷克波信源的传统TD-LSM
图1为TD-LSM应用场景示意图,其中Ω∈ℝd,d=2或d=3表示封闭待测区域,区域中存在位置固定的散射体D,其边界∂D连续,散射体外部记为电磁波在背景介质中速度稳定为c0,待测区域被位于曲线内的N个收发共置阵元测量,采用信息分量较为丰富的时域雷克波信号作为信源,其表达式如下:
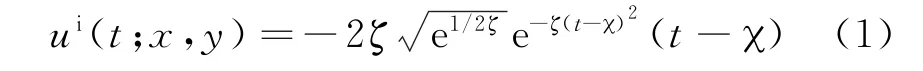
式中,ζ=2π2f2,χ=1/f,f表示主频,x,y∈ℝd,t∈[0,T]表示时间信号的长度,间隔为Δt,时间序列量化个数为N=T/Δt,x=[x1,x2]∈Ω表示采样点在待测区域中的坐标,y=[y1,y2]∈Γi表示入射阵元位置,根据时间信号的有序性,当t<0时,ui(t;x,y)≡0。根据惠更斯原理,对于信源照射到的待测区域中任意采样点x,若x存在散射系数,则可以将x看作是一个新的子波源,若τ表示子波源相对发射信号的时延,则反射波可以改写为

由此得到电磁波在自由空间传播过程中的波动方程、初始条件和边界条件:
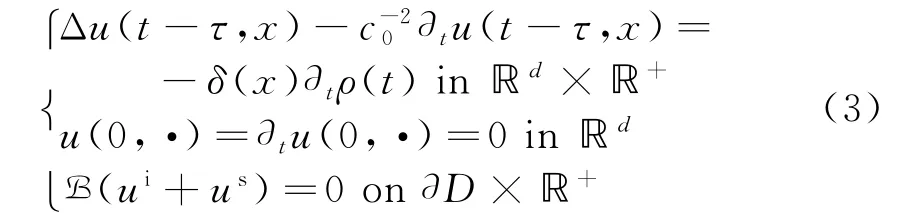
式中,τ为信号时延,c0为自由空间波速,δ为狄拉克函数,ρ(t)为单位阶跃函数,ui(·;x,y)为雷克波信号源激励,且在远场模式下,待测区域内的总场u(t;x,y)、入射场ui(t;x,y)以及散射场us(t;x,y)满足下式:

通过求解式(3)可以得到散射场us(·;x,y)的基本解:
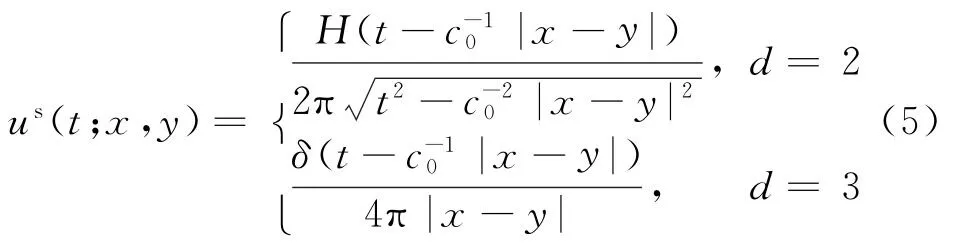
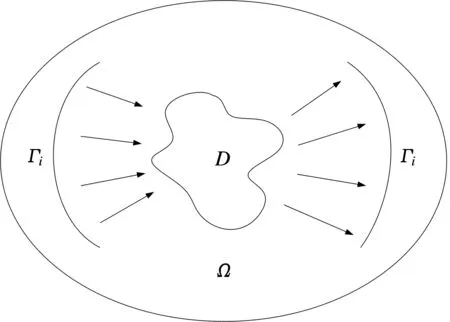
图1 场景示意图
因此,通过正演过程求解得到的us(t;x,y)即为通过数学表达获取的仿真实验数据,在实测实验中us(t;x,y)即为雷达天线阵列接收到的数据。利用TD-LSM求解逆问题,其本质就是在已知阵元位置的条件下,利用在不同入射角y n下的采集回波数据us(x,t;y n),对每个采样点求解式(6),从而在位置目标物理类型和几何形状未知的条件下,获取未知目标(若存在)的位置与边界外形信息:

由于时域数据具有因果时变特性,因此需要将左端数据矩阵FTD修改为离散卷积形式,若原始场景中包含M个收发共置阵元,每个阵元接收时间为t∈[0,T]内的数据,数据时间间隔为Δt,单个阵元的数据总长度为N=T/Δt,则得到FTD离散化形式:

再将离散形式数据矩阵重组为离散卷积形式后得到
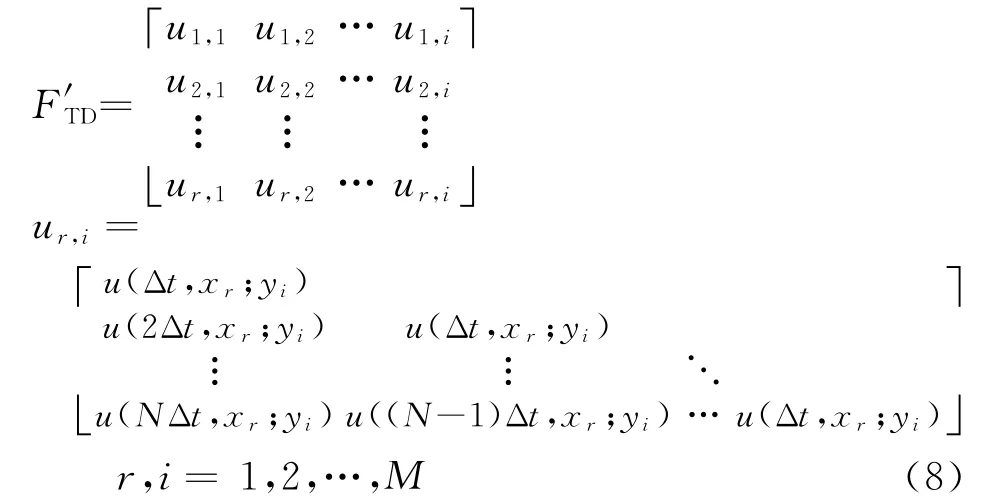
式中,y i表示第i个发射天线,x r表示第r个接收天线。若z为采样点坐标,τ为选取的时延,则利用所有入射方向y n∈Γi的接收数据对所有采样点z∈ℝ构建TD-LSM核心方程组:
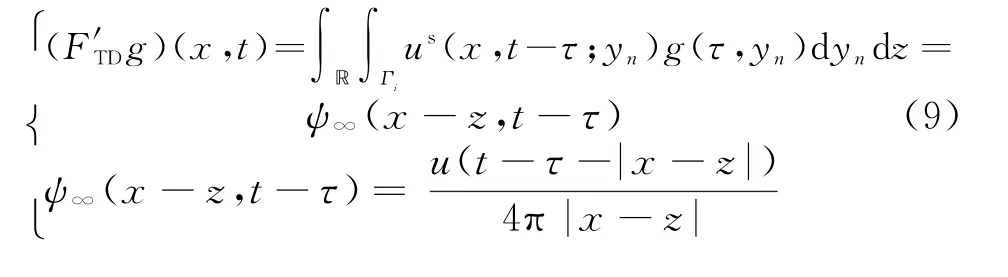
式中,ψ∞(x-z,t-τ)为远场检验函数,其数学模型与信源发射信号近似,通过求解式(9),并根据如下判断条件可以得到关于采样点z的相应结论:
1)若z∈D,且εr>0,则存在函数
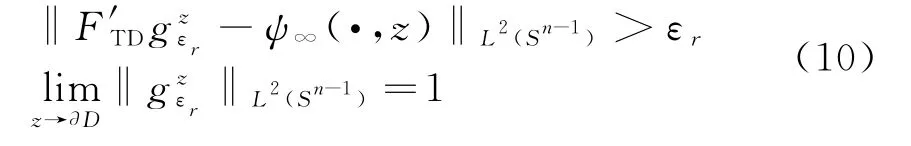
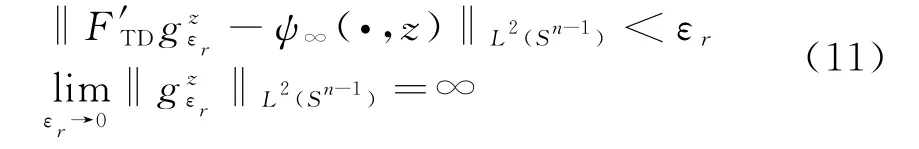
然而,由于求解式(9)为病态逆问题,因此需要引入Tikhonov正则化方法,利用F′TD的SVD分解参数{Utd,Std,Vtd}求出式(9)的可靠解g(z,τ),并求出其L2范数G(z,τ)作为像素点的指示器函数:
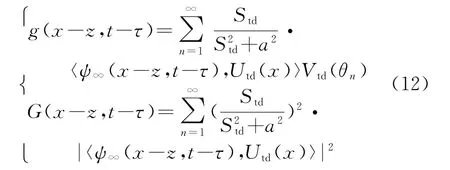
至此,直接利用时域数据对待测区域进行重构的原始TD-LSM主要步骤如下:
1)将式(9)中原始数据矩阵变换为离散卷积形式F′TD,并对其进行SVD分解得到{Utd,Std,Vtd};
2)将待重构场景进行离散化处理,选取某个特定时刻作为等式右端时延值,从第一个采样点开始选取,计算该时延下式(9)中的检验函数,并进行离散卷积化;
3)根据式(12)求出该采样点指示器G(z,τ),若G(z,τ)→0则z∈D,若G(z,τ)→ ∞ 则z∈
4)计算下一个采样点z n(n=1,2,3,…,N),重复步骤2)~3),直到遍历成像区所有采样点。
尽管TD-LSM克服了频域线性采样法需要大量数据点支撑的缺陷,同时避免了对时域数据进行傅里叶变换的操作,但传统TD-LSM同样存在缺陷,时延τ的选取没有理论化标准,通常依靠经验选取,因此,需要寻找一种可以替代经验选取时延值的方法;其次,由于等式左端数据矩阵变换为离散卷积形式,导致数据量异常增大,SVD运算异常缓慢。
2 TD-LSM改进算法
2.1 时延值最佳选取标准
针对时延τ的选取没有理论化标准,通常依靠经验选取的弊端,首先从吉洪诺夫原理入手,若获得原始数据矩阵F′的SVD分解参数{Utd,Std,Vtd}后,则原始数据可以表示为

式中,Utd={u1,u2,u3,…,u n},Vtd={v1;v2;v3;…;v n},Std=diag{s1,s2,s3,…,s n}。3个分解参数包含了整个原始矩阵的全部信息,其信息的重要程度按照奇异值矩阵Std依次递减。根据SVD分解原理,若存在一个矩阵与原始数据矩阵相似,则可以通过左右奇异矢量与相似矩阵还原原始分解矩阵。而时域线性采样法作用机理是在遍历采样点过程中选取一个特定σ时刻,计算该时刻下从每个采样点接收到的时域波形矩阵,再利用吉洪诺夫正则化验证每个采样点是否存在散射系数。若检验函数与原始数据矩阵相似,则根据式(9)、式(12)求解得到

式中,f(x-z,t-τ)表示原始数据矩阵分解出的奇异值参数。因此,当某个采样点计算出的检测函数与接收到信号相关程度最大时,可以通过式(12)判断该点存在散射系数。因此在TD-LSM中,选取有效的检验函数时延σ是一个重要环节,σ越接近原始数据接收回波中的时延值τ,其检验函数和接收数据函数相关度越高,其获得的结果越好。由于墙后目标通常未知,因此在缺少先验信息的条件下,无法有效地获得各个接收阵元的τ值,导致经验选取σ值的过程中容易与τ值产生较大误差。针对这一缺陷,接下来提出一种利用互相关原理寻找最佳检验函数时延σ值的方法,若u0(t)表示发射阵元零时信号,u i(t-τ)表示回波接收信号,τ为接收信号相对零时信号的时延,根据数据互相关原理得到
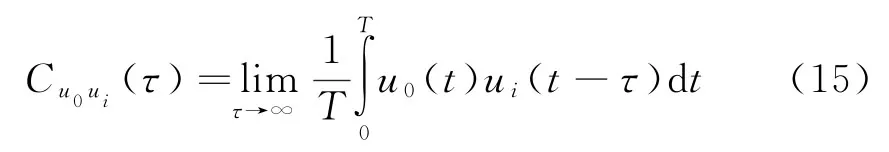
因为u0(t)与u i(t-τ)为相同信号,最佳时延准则是利用发射阵元零时信号与接收数据矩阵互相关,得到接收回波的时延时刻,使得在τ时刻达到最大值1,随后选取τ作为检验函数σ值。
通过正演实验验证最佳时延选取准则获取的σ值,首先分析在TD-LSM测量过程中的信号传播路径,如图2所示。从图2可以看出,在路径传播的过程中,存在散射体上的某点,与位置固定的两个阵元组成完整的信号路径,若将该点A看作子波源,可以等效获得A到达各个阵元的信号集合,对此信号集合补偿由阵元D到达A点的距离时延,便可使该信号达到与阵列中部分阵元的接收信号完全相关状态。

图2 信号传播路径示意图
根据3.1节仿真实验场景相同配置,仿真反射波到达各个阵元的正演过程,选取金属散射体前表面上正中心采样点,坐标(0.55,0.4),并在此添加一个发射阵元,发射与仿真实验相同的时域雷克信号波,其他阵元作为接收端,获取此场景下的验证接收数据,如图3所示。其中,图3(a)中补偿1曲线表示对验证数据补偿第11号阵元到达点(0.55,0.4)的时延后,与该组数据的互相关系数曲线;补偿2曲线为补偿第14号阵元到达该点的时延后,验证接收数据与该组互相关系数曲线;未补偿曲线表示不补偿14号阵元到达该点的距离时延,验证接收数据与阵列阵元的互相关系数。图3(b)中3条曲线分别表示检测函数在0.25 ns,0.75 ns和1.25 ns时延下,与第11组接收数据的互相关系数曲线,这组验证实验表明,0.75 ns为较为合适的时延值选择。图3(c)表示检测函数在0.75 ns时延下与第5组、第11组、第16组接收数据的互相关系数曲线,这组验证表明该点信号较为接近第5组阵元的回波散射点。通过正演实验可以发现,互相关函数可以寻找两列信号最相似的时刻,利用这个特性,可以提高时延选取效率,验证了最佳时延选取准则的有效性。
2.2 基于数据分割思想的TD-LSM
由于TD-LSM需要对采集数据进行离散卷积变化,导致参与运算的数据维数严重膨胀,针对这一缺陷,进一步提出一种基于数据分割思想的TDLSM改进。从图4可以看出,TD-LSM成像过程中以采样点作为循环变量。利用这一特性,在遍历成像区域采样点的过程中,首先计算各个天线到达该点的时延范围τ1~τn,找出时延范围中的最大值τmax和最小值τmin,随后从离散卷积变换后的数据中截取位于[τmin,τmax]子区间内的数据作为有效数据,再对有效数据进行离散卷积化变形和运算,以此达到数据压缩提高运算效率的目的。至此,基于分割思想且符合最佳时延选取准则的TD-LSM改进方法步骤为:
1)利用各个发射阵元的零时信号与各组接收信号进行互相关运算获取接收时延的集合,计算时延集合的均值作为检验函数的时延值;
2)将待重构场景进行离散化处理,从第一个采样点依次遍历选取,计算每个采样点到达各个阵元的时间范围作为该采样点的有效数据区间,从原始数据中剔除落于有效区间外的冗余数据,随后将其离散化重组并进行SVD分解获得相应的分解参数{U′td,S′td,V′td};
3)利用步骤1)获取的时延值,计算该时延下采样点到各个阵元的检验函数,并重组为离散卷积形式;
5)对下一个采样点z n(n=1,2,3,…,N)重复步骤2)~4),直至遍历所有采样点。
3 结果分析
3.1 仿真实验
通过仿真和实测数据对本文提出的算法进行验证,并采用如下几个评判标准:利用平均运行时间(APRT)判定算法执行时间,APRT越小代表算法运行时间越短;利用均方根误差(RMSE)判定成像效果与原散射体位置偏离程度,RMSE值越小成像结果越接近原散射体位置;利用一阶差分均值法(MFOD)判定轮廓特性,MFOD值越小检测区域越平滑;利用图像熵(ENT)判定成像复杂度,ENT值越小整幅图杂波越少,其中RMSE和MFOD为无纲量参数。
首先仿真实验信源采用主频为1 GHz的雷克波,整体场景大小为边长1.05 m的正方形,数据采集装置采用20个收发共置阵元组成的线阵,阵元间隔0.05 m,距离墙体0.05 m,从x轴0.05 m处开始向x轴正方向延伸。墙体厚度0.1 m,墙体前表面距离边界0.1 m,白色为墙体位置,黑色为目标金属矩形物体,三角形表示各个阵元,左下角坐标位于(0.4,0.4),右上角坐标位于(0.7,0.45),如图5(a)所示。
从图5(b)~图5(d)可以看出,TD-LSM选取时延τ值无论过大还是过小都会影响最终成像结果的精确度。根据本文提出的最佳时延选取准则,最佳的时延σ值范围在真实目标到各个阵元的平均时延上下浮动,因此在这一准则下,最佳时延范围应在整个金属前表面上各个采样点到各个阵元的平均时延,直接根据仿真场景配置计算可得7.564 4 ns。仿真结果验证了最佳时延选取准则以及选取时延的改进方法。
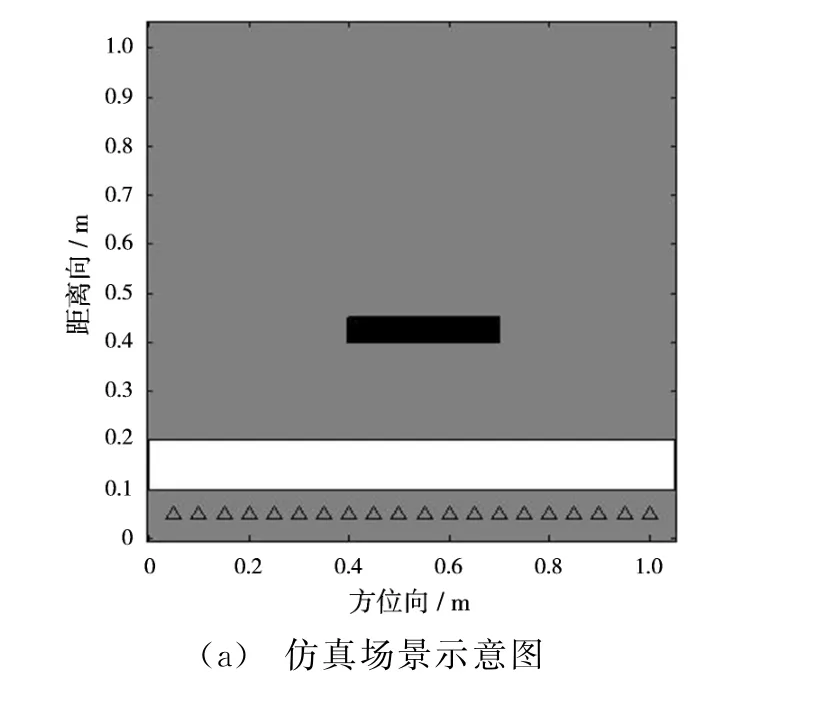
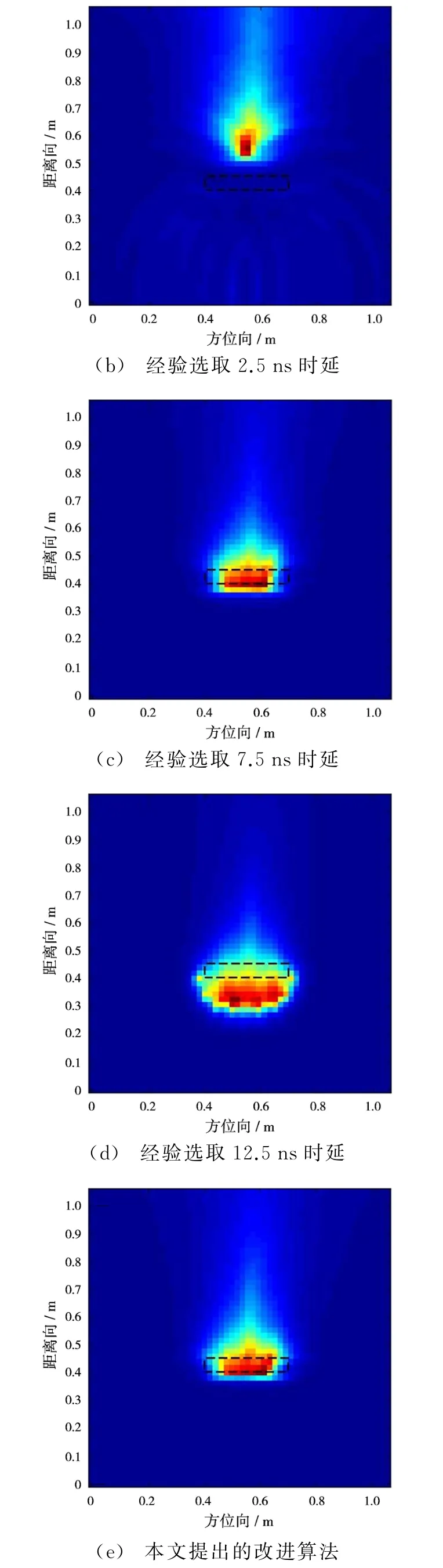
图5 经验选取时延与本文提出的改进方案对比
表1给出了图5中4组成像结果的APRT,RMSE,MFOD和ENT的比较参数。从表中可以看出,尽管第1组结果中的MFOD值最小,说明其成像结果轮廓最好,但是RMSE值和ENT值较大,说明其结果与散射体真实位置和形状偏差较大且图像中杂波较多;第2组结果中,由于选取了接近最佳选取准则计算得到的时延值,因此,其RMSE值相比第1组性能提高约30%,ENT值相比第1组性能提高约17%,结果说明其结果较为准确,可信度较高且杂波较少,由于成像结果较为接近散射体位置和形状,因此导致MFOD值相对略有增加;第3组结果中,由于选取时延值再次违背最佳时延准则,尽管其ENT值为4组数据中最小,但其RMSE值和MFOD值均为4组结果中最差,其结果十分不可靠;最后一组结果中,相对于第2组数据,尽管牺牲了小部分MFOD值和ENT值为代价,换取获得RMSE值最优和运算效率显著提升,表明本文提出的算法不仅可靠性最佳且运算效率最大。
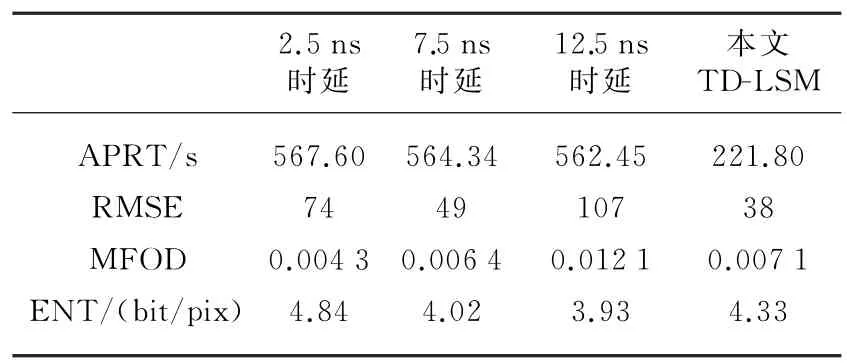
表1 几种时延取值下运算效果对比
3.2 实测实验
实测实验选取法国菲涅尔实验室提供的散射场数据来对本文提出的算法进行验证。实验目标规格为80 mm×50 mm,一侧缺口为40 mm的金属立方体,位于测试区域中心,发射天线位于半径为0.72 m的圆阵上,入射角度范围0°~350°(间隔10°),接收天线位于半径为0.76 m的圆阵上,接收角度范围60°~300°(间隔10°),频率范围为1~8 GHz,步进1 GHz。
从图6(a)~图6(d)的频域成像结果可以看出,成像结果杂波和虚像较多,而低频部分结果边界连续性和平滑性较差。相较于单频或多频提取方法的结果,图6(e)和图6(f)中的传统TD-LSM和改进TD-LSM直观上可以较为良好的兼顾二者。


图6 几种不同算法的成像结果对比
表2给出了4组方法的APRT,RMSE,MFOD和ENT的比较结果。第1组结果中,尽管ENT值最佳,但是MFOD值较差;第2组结果中,相较第1组结果,仅仅提升了MFOD值,RMSE值和ENT值均下降,造成这一结果的主因,是该场景中U型金属缺口部分仅有部分正对阵元可以提供真实的信息情况,而其他部分的阵元无法透过金属外壳获取U型缺口内部信息;第3组结果中,运行时间大幅增加,但是RMSE值、MFOD值和ENT值均提升有限;而本文提出的改进算法在尽可能保证重构质量的情况下,最大幅度地减少运算时间。

表2 实测实验算法对比
4 结束语
通过对传统TD-LSM的数值公式分析,获得线性采样类方法的核心步骤为利用正则化方法求解病态解逆问题。随后,分析了TD-LSM算法特点和数据结构特点,找到了检验函数时延值的选取是影响成像效果的重要参数。针对检验函数时延值的选取没有标准化的流程和方法,结合信号互相关原理,提出一种TD-LSM最佳时延选取准则,并通过正演实验进行分析验证。之后进一步通过分析信源在整个待测区域的走时过程,进一步提出一种基于分割思想的TD-LSM改进,利用采样点到各个阵元的距离范围,有效地剔除原始数据矩阵中的冗余信息,大大提高了运算效率。
[1]COLTON D,MONK P.Linear Sampling Method[M].US:Society for Industrial&Applied Mathematics,1999.
[2]NAKAMURA G,WANG H.Linear Sampling Method for the Heat Equation with Inclusions[J].Inverse Problems,2013,29(29):104015.
[3]AUDIBERT L,HADDAR H.A Generalized Formulation of the Linear Sampling Method with Exact Characterization of Targets in Terms of Farfield Measurements[J].Inverse Problems,2014,30(3):035011.
[4]BAZÁN F S V,FRANCISCO J B,LEEM K H,et al.Using the Linear Sampling Method and an Improved Maximum Product Criterion for the Solution of the Electromagnetic Inverse Medium Problem[J].Journal of Computational and Applied Mathematics,2015,273(C):61-75.
[5]ERRAMSHETTY M,BHATTACHARYA A.Shape Reconstruction of Mixed Boundary Objects by Linear Sampling Method[J].IEEE Trans on Antennas and Propagation,2015,63(7):3077-3086.
[6]ARAMINI R,BRIGNONE M,PIANA M.The Linear Sampling Method Without Sampling[J].Inverse Problems,2006,22(6):2237.
[7]CARAYOL Q,COLLINO F.A Sampling Method for Inverse Scattering in the Time Domain[J].ESAIM:Mathematical Modelling and Numerical Analysis,2004,38(2):371-394.
[8]GUO Y,MONK P,COLTON D.The Linear Sampling Method for Sparse Small Aperture Data[J].Applicable Analysis,2015,95(8):1599-1615.
[9]KHAJI N,MANSHADI S H D.Time Domain Linear Sampling Method for Qualitative Identification of Buried Cavities from Elastodynamic over-Determined Boundary Data[J].Computers&Structures,2015,153(2):36-48.
[10]HADDAR H.An Improved Time Domain Linear Sampling Method for Robin and Neumann Obstacles[J].Applicable Analysis,2014,93(2):369-390.
[11]CHEN B,MA F,GUO Y.Time Domain Scattering and Inverse Scattering Problems in a Locally Perturbed Half-Plane[J].Applicable Analysis,2017,96(8):1303-1325.
