一种新的近程多目标轨迹参数测量方法∗
2018-01-21郭新民
郭新民,吕 鹏
(1.中国人民解放军92785部队,河北秦皇岛066000;2.北京理工大学信息与电子学院,北京100081)
0 引言
制导武器的性能一般在弹、靶遭遇段得到较为集中的体现,而武器的杀伤效果与制导精度密切相关。为了准确分析武器系统的误差因素,需要测量弹、靶遭遇段数据以鉴定武器系统的制导精度,判定杀伤效果[1]。近年来,随着武器技术的飞速发展,齐射弹和子母弹等多目标武器层出不穷,而现有的单目标轨迹参数测量系统无法满足多目标测量的需求。因此,研究近程多目标轨迹参数测量技术对多目标武器命中精度的鉴定有着广泛的应用价值。
文献[2]通过一系列图像处理技术可以得到多目标脱靶量参数的精确估计结果,但是这种方法缺乏数据关联,需要人来判断“时间 多普勒”变化曲线。文献[3]在多目标脱靶量测量中引入数据关联,该方法在从测量结果到跟踪航迹的关联上执行良好,并且在后续处理中提供矢量脱靶量参数的可靠估计。但是这种方法是建立在传统的回波信号模型基础上,具有较低的距离分辨率和频率分辨率。数据关联是多目标轨迹参数测量的关键技术之一,数据关联算法性能的优劣直接影响测量系统的整体性能。概率多假设跟踪(Probabi-listic Multi-Hypothesis Tracking,PMHT)算法自Streit和Luginbuhl提出以来,主要用于多目标跟踪过程中多目标点迹的数据关联。近年来,一些基于PMHT的算法被应用到其他一些非传统跟踪的领域中,如对柱状图量测数据、高光谱数据及红外图像的处理等。
为了克服文献[2-3]中出现的问题,本文利用目标交会过程中多普勒频率随时间变化的规律,提出了一种新的基于无线电测量技术的多目标轨迹参数测量方法。首先,基于逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)成像技术对目标回波进行“距离-多普勒”成像并提取多个目标的距离及多普勒频率信息;然后,对“距离-多普勒”图像进行峰值提取,获得径向距离及多普勒频率随采样时间的变化数据,利用PMHT算法对该数据进行数据关联,从而获得稳定的多个目标的距离和多普勒频率随时间变化数据;最后,利用非线性最小二乘方法对多个目标的多普勒频率随时间变化数据进行非线性最小二乘拟合,进而得到多目标的运动轨迹参数。
1 多目标的多普勒频率模型
在导弹攻击目标运动过程的末段,通常可认为是匀速直线运动。假设多目标轨迹参数测量设备安装于靶标上,导弹相对靶标作匀速直线运动[4]。假设两个点目标朝向测量天线作匀速直线运动,测量天线与目标的几何关系如图1所示。目标运动轨迹所在直线与测量天线之间的最近距离点称作脱靶点。假设目标运动的初始时刻作为时间参考点t=0,此时目标1和目标2的速度分别为v1和v2,两目标起始位置与脱靶点之间的初始切向距离分别为L1和L2,脱靶点与测量天线之间的距离分别为r1和r2,即标量脱靶量。

图1 测量天线与目标的几何关系
假设多目标轨迹参数测量设备(以下简称测量设备)发射波长为λ的射频信号,由于目标和测量设备之间的相对运动,根据多普勒效应,目标1和目标2的回波信号产生的多普勒频率f(t)为

因此,只要设法测量出弹靶交会过程中导弹反射回波的多普勒频率随时间的变化,即可得到弹靶之间相对运动的径向速度分量,从而可进一步拟合出标量脱靶量[5-6]。根据式(1),图2给出了两组典型参数条件下匀速直线运动目标的多普勒频率随时间变化规律曲线。其中目标运动速度分别为800 m/s和400 m/s,脱靶量分别为10,20,30,40和50 m。由图2可知,在给定发射信号波长为λ的情况下,多普勒频率可由目标轨迹参数r,v和L唯一确定。因此,通过对回波信号中多个目标不同的多普勒频率随时间变化曲线进行非线性最小二乘拟合,就可以得到多目标的运动轨迹参数。
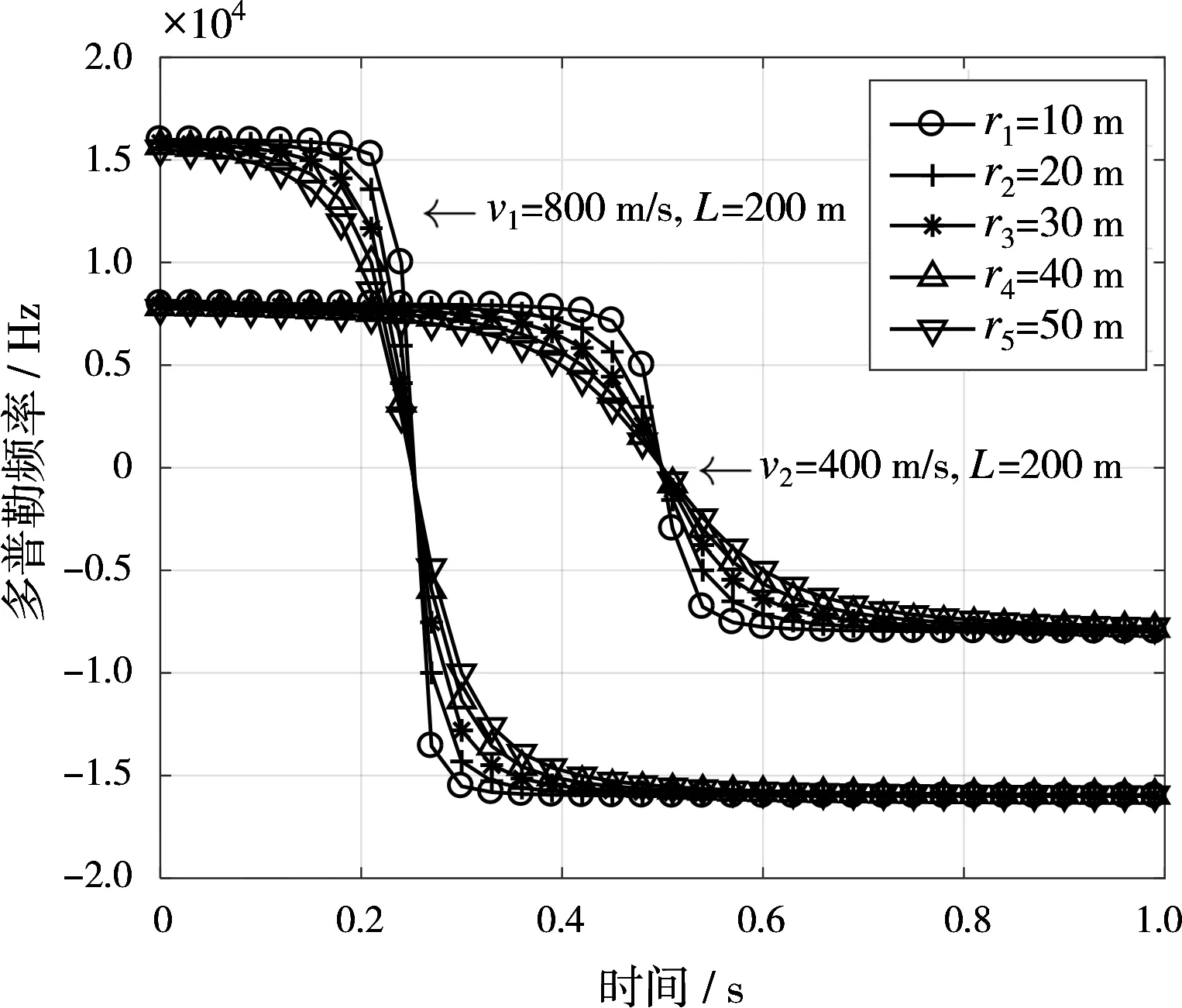
图2 不同参数条件下目标交会段目标多普勒频率随时间变化规律
2 近程多目标轨迹参数测量方法
2.1 ISAR成像基本原理
在基于多普勒频率的多目标轨迹参数测量中,多普勒频率的提取是其中的关键环节。传统的方法是用模拟或脉冲技术式鉴频器从目标多普勒信号中检测出多普勒频率[7]。本算法采取ISAR技术提取运动目标的距离与多普勒频率信息,具有较高的精度。
逆合成孔径雷达对运动目标具有高分辨二维成像能力,在弹道导弹防御等方面具有重要的应用价值,它利用与目标间的相对运动形成合成阵列来提高横向分辨率,通过发射大带宽信号并对目标回波进行脉冲压缩处理得到径向距离上的高分辨率,根据目标的横向和距离向的信息进而得到目标成像[8-10]。假设ISAR采用大带宽线性调频信号形式,其一般原理框图如图3所示。

图3 ISAR成像原理框图
目标回波信号经混频器处理为中频信号后送至中频放大器作放大处理,再经匹配滤波进行脉冲压缩处理获得目标的一维距离像,再进行正交检波以检测信号的幅度和相位信息,通过采样器和模数转换器对正交检波输出的I,Q通道信号进行采样和数字化处理。对于目标的同一点而言,N个脉冲回波信号经处理后产生N个距离像,每个距离像被量化为M个距离单元,每个距离单元并排放置以对准相应的距离位置[11]。
在对二维数据集中的目标回波信息作距离补偿后,沿着方位角时间作一维离散傅里叶变换(Discrete Fourier Transform,DFT),将目标回波时域信号变换到频域空间,所得到的二维矩阵即是目标的“距离-多普勒”ISAR图像。
2.2 PMHT算法
PMHT算法假设在每次天线扫描中一个目标可产生多个回波,且假定量测、目标的关联过程在量测之间是互相独立的,采用期望最大算法(Expectation Maximization,EM)得到一种在最大似然估计下的最优跟踪算法。PMHT算法避免了联合概率数据关联算法(Joint Probabilistic Data Association,JPDA)穷举所有可能关联事件的弊端,使其计算量与量测和目标数量呈线性关系[12-14]。PMHT算法采用批处理的方式,通过有限次的循环迭代以优化航迹与回波的关联,以求解状态的最优估计。
假设被测区域内存在M个目标,第i个目标的状态方程和量测方程分别为
式中:i=1,2,…,M,x i(t)为第i个目标t时刻的运动轨迹;z i(t)为第i个目标t时刻的量测值;F i(t)为系统状态转移矩阵;H i(t)为观测矩阵;w i(t)为目标状态方程的建模误差;v i(t)为观测噪声,并假定w i(t)和v i(t)都是零均值的高斯白噪声,且是不相关的两个噪声序列。
为利用已知的量测值求得目标的最佳状态估计,令X={x i(t)},Y={y j(t)},其中y j(t)表示t时刻第j个量测值,S={s j(t)},其中s j(t)表示在t时刻第j个量测值来源于第s j(t)个目标。令第j个量测值来源于第i个目标的先验概率是πi,即P(s j(t)=i)=πi,设定参数模型y j(t)=z sj(t)(t)。
对T个扫描周期的量测进行批处理循环迭代以求得最优的目标状态估计。对于第l次迭代,计算t时刻第j个量测值对应于目标i的后验关联概率为

式中,P i(t)为一个量测来源于目标i的先验概率,且假设先验概率是相互独立的,目标i=1,2,…,M,时间t=1,2,…,T,量测j=1,2,…,n t。

2.3 非线性最小二乘参数估计
近程多目标轨迹参数估计原理是弹靶交会过程中目标回波的多普勒频率随时间而变化,变化规律由导弹与靶标的相对速度v、导弹运动轨迹与靶标最近点的距离,即标量脱靶量r,以及起始位置与脱靶点之间的距离L共同决定。对应不同的参数,多普勒频率随时间的变化规律也不相同。因此,只要测得交会过程目标回波多普勒频率随时间的实际变化曲线,采用最优化方法对其作最优拟合,就可得到标量脱靶量参数[16-18]。这种方法的优点在于易克服测量设备在低空、地面或海面工作时杂波的影响,而且可以实现大脱靶量的测量[19]。

3 计算机仿真
为了验证本文方法的有效性,对所提方法进行了计算机模拟仿真。假设3个点目标分别同时向测量天线作匀速直线运动,测量天线与目标的几何关系如图1所示,仿真参数如表1所示,发射信号为线性调频信号,波长λ为0.1 m,在回波基带信号中添加信噪比为10 dB的高斯白噪声,对算法进行了500次蒙特卡洛仿真,分别使用JPDA和PMHT算法对“时间 距离-多普勒”数据进行了数据关联,并统计3个目标的运动参数估计结果的均值和均方根误差(Root Mean Square Error,RMSE)。仿真程序运行的平台配置为:英特尔Core i5 750处理器,主频为2.67 GHz;8 GB DDR3内存;MATLAB 2017a软件。
图4是经过ISAR处理后得到的“距离-多普勒”图像。图5是对图4数据进行峰值提取之后的“时间-距离-多普勒”数据。图6是经过使用PMHT算法进行数据关联之后的结果。由仿真结果可以看出,ISAR成像获得了3个目标的距离和多普勒频率随时间变化信息,并通过峰值提取的方法快速有效地同时获得多个目标的“时间-距离-多普勒”数据,最后经数据关联算法对3个目标的“时间-距离-多普勒”数据进行数据关联。

表1 仿真参数设置

图4 “距离-多普勒”图像
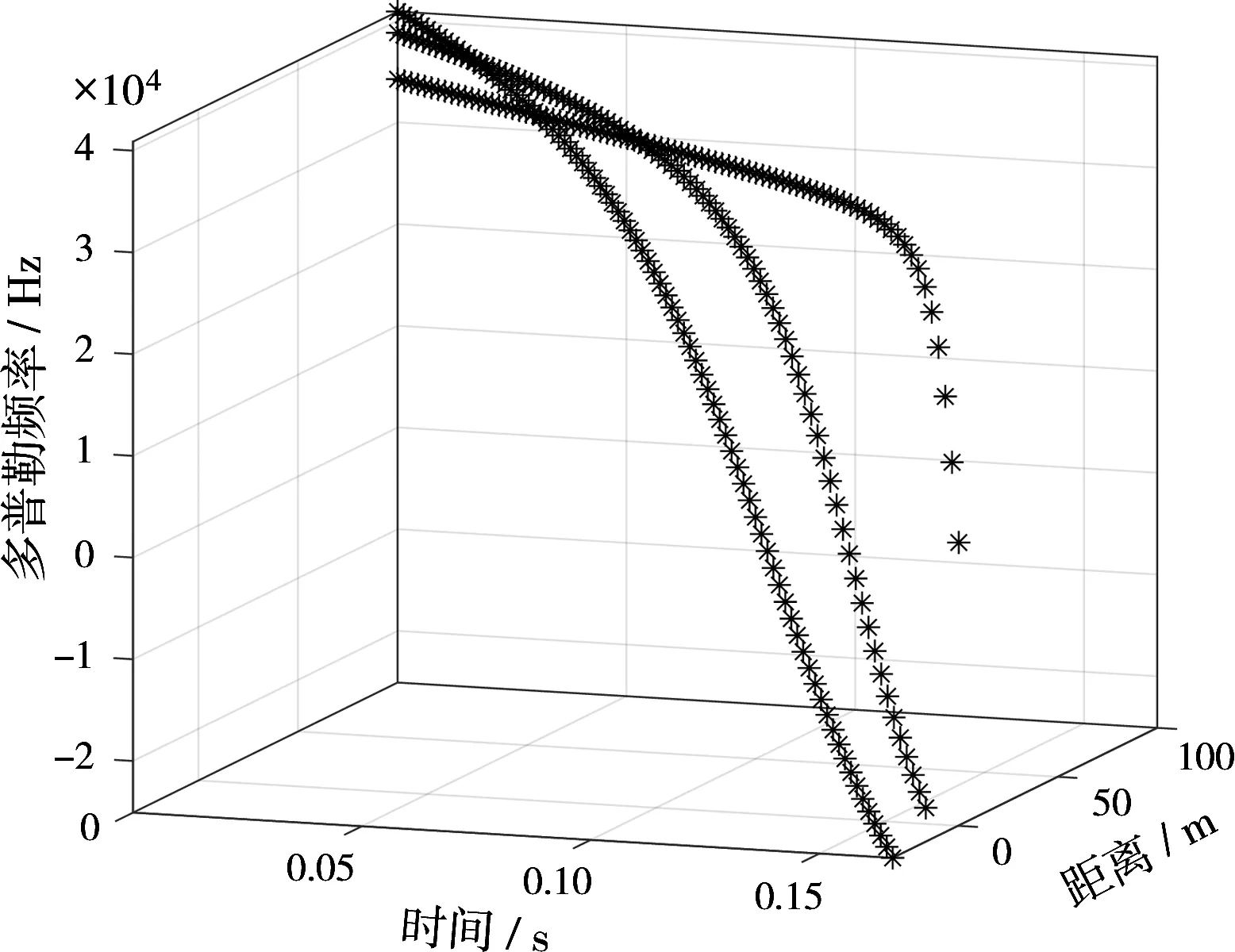
图5 “时间 距离 多普勒”曲线

图6 经过数据关联的“距离-多普勒”图像
表2列出了3个目标使用本文所提方法后,分别使用JPDA算法和PMHT算法进行数据关联后的参数估计结果,其中使用JPDA算法数据处理时间为3.21×104s,PMHT算法数据处理时间为2.44×104s。从仿真结果可以看出,在本文所提数据处理框架下,在数据关联过程中使用JPDA算法或者PMHT算法都可以得到较为满意的运动参数估计结果,但PMHT算法运算速度更快、效率更高。由于PMHT算法对多目标运动过程中产生的“交叉数据”采取延迟关联的方式,因此在对存在数据交叉的情况下,PMHT算法会比JPDA算法获得更高的参数估计精度。

表2 多目标轨迹参数估计结果
4 结束语
本文提出了一种新的基于无线电测量技术的多目标轨迹参数测量方法。该方法在一定的传感器布局条件下,充分利用多个目标与测量天线相对运动过程中产生的多普勒频率和距离数据进行数据关联,将多目标空间运动参数测量问题简化为多个单目标空间运动参数测量问题,最后通过非线性最小二乘拟合进行参数估计。仿真结果表明,该方法可以有效地提取多个目标的距离及多普勒频率信息并进行目标运动轨迹参数测量,具有较高的精度。因此,本文提出的方法对于进一步研究多目标轨迹参数的高精度测量具有重要的借鉴意义。
[1]冯定伟,吴嗣亮,魏国华.基于多普勒频差的矢量脱靶量参数估计方法[J].系统工程与电子技术,2012,34(8):1530-1535.
[2]HOU Shujuan,WU Siliang.Multi-Targets Miss Distance Measurement Based on a Sequence of Image Processing Techniques[C]∥8th International Conference on Signal Processing,Beijing:IEEE,2015:1367-1371.
[3]FANG Bingyi,WU Siliang.Multiple Targets Vector Miss Distance Measurement Accuracy Based on 2-D Assignment Algorithms[J].Journal of Systems Engineering and Electronics,2008,19(1):76-80.
[4]冯定伟,吴嗣亮,魏国华.基于多普勒频率的脱靶量参数估计性能分析[J].北京理工大学学报,2016,36(1):94-99.
[5]蔺建英,马海潮.基于单站序列图像的导弹脱靶量测量方法[J].航天控制,2013,31(5):41-45.
[6]杨琳,孟宪国,朱元昌,等.基于仿真推演的高炮射击脱靶量解算方法[J].火力与指挥控制,2013(11):72-76.
[7]ÖZDEMIR C.Inverse Synthetic Aperture Radar Imaging with MATLAB Algorithms[M].Hoboken:Wiley,2012.
[8]刘承兰,高勋章,黎湘.干涉式逆合成孔径雷达成像技术综述[J].信号处理,2011,27(5):737-748.
[9]刘波,李道京,李烈辰.基于压缩感知的干涉逆合成孔径雷达成像研究[J].电波科学学报,2014,29(1):19-25.
[10]朱小鹏,张群,罗迎,等.基于调频连续波的双基逆合成孔径雷达研究[J].电波科学学报,2011,26(4):771-776.
[11]武光辉,童创明,李西敏,等.逆合成孔径雷达目标成像识别优化仿真[J].计算机仿真,2016,33(6):9-12.
[12]范炳艺,李建勋,刘坦.面向目标的概率多假设跟踪算法[J].航空学报,2010,31(12):2373-2378.
[13]李世忠,王国宏,白晶,等.压制干扰下雷达网点目标概率多假设跟踪算法[J].西安交通大学学报,2012,46(10):101-106.
[14]申屠晗,郭云飞,薛安克.声探测网络延时概率多假设跟踪算法[J].计算机仿真,2011,28(1):352-355.
[15]WIENEKE M,KOCH W.A PMHT Approach for Extended Objects and Object Groups[J].IEEE Trans on Aerospace&Electronic Systems,2012,48(3):2349-2370.
[16]王江荣.基于卡尔曼滤波算法的最小二乘拟合及应用[J].自动化与仪器仪表,2013(3):140-142.
[17]侯俊峰,王东光,邓元勇,等.基于最小二乘拟合的波片相位延迟测量[J].光学学报,2011,31(8):104-109.
[18]王江荣.基于小波分析的最小二乘拟合及应用[J].自动化仪表,2012,33(2):19-21.
[19]冯定伟,吴嗣亮,魏国华.基于多普勒频差的矢量脱靶量参数估计方法[J].系统工程与电子技术,2012,34(8):1530-1535.
