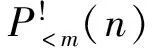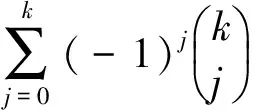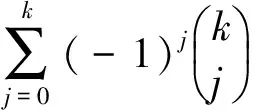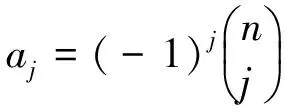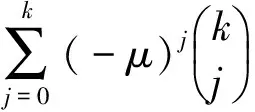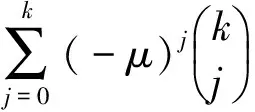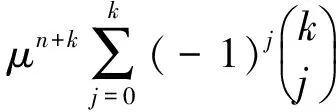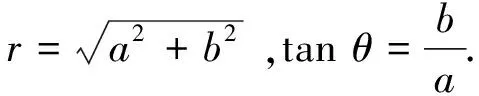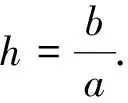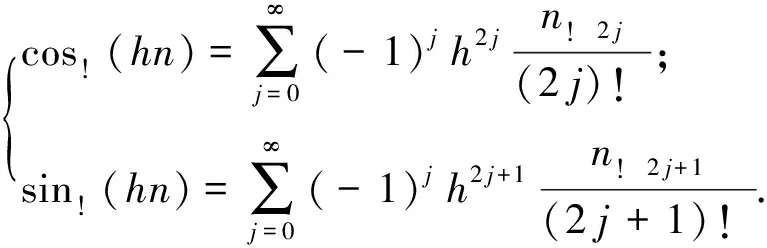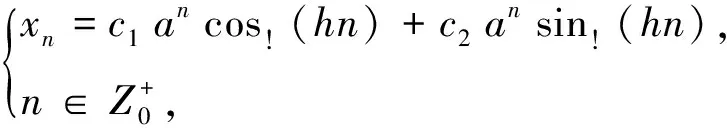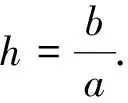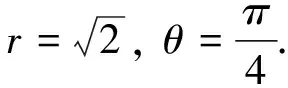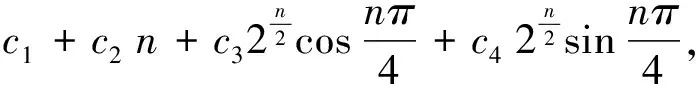解简单差分方程的方法及其改进
2018-01-19孙建新
孙建新
(绍兴文理学院 数理信息学院,浙江 绍兴 312000)
文献[1]研究了拟初等函数,文献[2]研究了函数展开为阶乘幂级数的方法.下面可以看到,上述两种研究成果,可得到差分方程求解的新方法.因为新方法建议在差分方程中将所有的普通幂转换成阶乘幂,所以可以称新方法为“阶乘幂方法”.事实上,普通幂转换成阶乘幂,又相当于函数转换成拟初等函数,所以,新方法也可以称为“拟初等函数法”.
1 差分方程的两种形式
离散函数有两种表示方法.一种是函数法,即表示成自变量为非负整数的函数:
另一种是数列法,即下标法:
xn,yn,zn,n=0,1,2,….
差分方程也有两种表示形式,一种是仅使用向前(向后)差分算子 Δ()的方程形式,以线性差分方程为例,k阶差分方程可以表示为:
Δkxn+p1(n)Δk-1xn+…+
pk-1(n)Δxn+pk(n)xn=q(n);
pk-1(n)xn+pk(n)xn=q(n).
另一种是移位算子E的方程形式:
Ekxn+p1(n)Ek-1xn+…+
pk-1(n)Exn+pk(n)xn=q(n).
记I为恒等算子,则差分算子与移位算子满足如下关系:
Δ=E-I=E,
=I-E-1=E-1Δ;
E=I+Δ,
E-1=I-.
当系数pj(n)=aj(j=1,…,k)都与n无关时,就称其为常系数的;当q(n)=0时,就称其为齐次的.对于常系数的齐次线性差分方程的两种形式:
Δkxn+a1Δk-1xn+…+
ak-1Δxn+akxn=0;
(1)
Ekxn+b1Ek-1xn+…+
bk-1Exn+bkxn=0.
(2)
它们之间存在较简单的关系,即有如下定理:
定理1.1 设方程(1)的特征根为λj(j=1,…,k),方程(2)的特征根为μj(j=1,…,k),则有
μj=λj+1,(j=1,2,…,k) .
证明方程(1)可以改写成
(Δk+a1Δk-1+…+ak-1Δ+akI)xn=0;
即
Δk+a1Δk-1+…+ak-1Δ+akI=0;
(Δ-λ1I)(Δ-λ2I)…(Δ-λkI)=0,
其中λj(j=1,…,k)为方程(1)的特征根,于是有
……
由Δ=E-I,方程(1)可化为
(E-I-λ1I)(E-I-λ2I)…
(E-I-λkI)=0;
(E-(1+λ1)I)(E-(1+λ2)I)…
(E-(1+λk)I)=0.
(3)
另一方面,由方程(2)可得
(Ek+b1Ek-1+…+bk-1E+bkI)xn=0;
Ek+b1Ek-1+…+bk-1E+bkI=0;
(E-μ1I)(E-μ2I)…(E-μkI)=0,
(4)
μj(j=1,…,k)
为方程(2)的特征根.于是有
……
比较式(3)和式(4)即得,证毕.
2 一阶差分方程
2.1 较简单的一阶差分方程
方程xn+1=axn+b,其中a,b为常数.
(ⅰ)当a=1时
xn+1=xn+b.
⑸
则有
可知满足方程的离散函数就是等差数列.
(ⅱ)当a≠1,b=0时
xn+1=axn,
(6)
则有
可知满足方程的离散函数就是等比数列.
(ⅲ)当a≠1,b≠0时
xn+1=axn+b,(a≠1,b≠0).
若记
(7)
x*称为差分方程的平衡点(或不动点).令
yn=xn-x*,
则有
yn+1=ayn.
(8)
比较式(6)与式(8),可得
即
综合以上结果可得如下定理:
定理2.1 一阶差分方程
xn+1=axn+b, (a≠1).
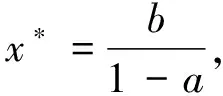
2.2 一般的变系数一阶差分方程
仅考虑两个特例.
例1)xn+1=an2xn.
该差分方程的通解为
例2)xn+1=axn+bn+c.
定理2.2 一阶常系数非齐次线性差分方程
xn+1=axn+bn+c
的解为
其中
证明若a=1,则递推可得
xn=xn-1+b(n-1)+c=
xn-2+b(n-2)+b(n-1)+2c=…=
若a≠1,则
xn+1+A(n+1)+B=
axn+(bn+c)+An+A+B=
axn+(A+b)n+(A+B+c).
令
(A+b)n+(A+B+c)=a(An+B),
解得
此与定理2.2结果等价,命题获证.
例3)xn+1=3xn+2n+1,求差分方程的解.
解:由a=3,b=2,c=1, 即得A=1,B=1.于是
xn+1+(n+1)+1=3xn+2n+1+(n+2).
xn+1+(n+1)+1=3(xn+n+1).
令yn=xn+n+1.可得yn+1=3yn.则
yn=xn+n+1=3ny0=3n(x0+1),
解得
xn=yn-n-1=3n(x0+1)-n-1.
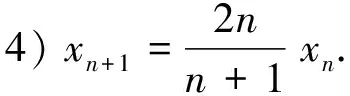
解:原方程可化为
(n+1)xn+1=2nxn.
令yn=nxn,则有
yn+1=2yn.
于是
yn=2ny0=2n(nx0).
解得
xn=2nx0.
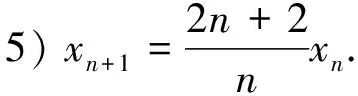
解:原方程可化为
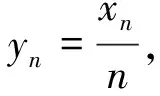
yn+1=2yn.
于是
yn=2n-1y1=2n-1x1.
解得
xn=n2n-1x1,n=1,2,….
3 常系数齐次线性差分方程的通解
对于常系数齐次线性差分方程来说,由定理1.1可知,存在差分形式(1)与移位算子形式(2).形式(2)又等价于:
xn+k+b1xn+k-1+…+bk-1xn+1+bkxn=0.
(9)
当q(n)≠0时,下面的方程
xn+k+b1xn+k-1+…+
bk-1xn+1+bkxn=q(n).
(10)
称为k阶常系数非齐次线性差分方程.式(9)称为与式(10)对应的齐次方程.
不妨设μ1,μ2,…,μk为方程(9)所对应的特征方程
μk+b1μk-1+…+bk-1μ+bk=0.
(11)
的特征根.下面是关于齐次方程(9)的通解的几个定理.
定理3.1 当特征根μ1,μ2,…,μk为k个互不相同的实根时,齐次方程(9)的通解为
(12)
证明考虑齐次线性差分方程的E形式(2),不妨设xn=μn, 则
Exn=Eμn=μn+1=μ·μn=μ·xn,
进而有
Ejxn=μj·xn,j=2,3,…,k.
于是方程(2)等价于
μkxn+b1μk-1xn+…+bk-1μxn+bkxn=0.
若xn=0,显然包括在通解(12)中(只要取c1=c2=…=ck=0);若xn≠0,则必有特征方程(11)式成立.即齐次线性差分方程(2)的非零解,形如xn=μn(μ≠0).
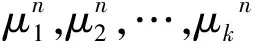
定理3.2 当特征根μ1,μ2,…,μk为k个相同的实根μ(即为k重实根)时,齐次方程(9)的通解为
xn=c1μn+c2nμn+…+
(13)
其中P 证明首先,由差分恒等式 可知 其中 cmn!0, (n!0=1). 其中S1(m,j)与S2(m,j)分别是第一类与第二类stirling数[5].于是 ΔkP 特别地,对于P Δknm=(E-I)knm= (m (14) 其次,当μ是差分方程(2)的k重特征根时,有 当m (E-μI)k(nmxn)= (m 这就证明了nmxn(m=0,1,…,k-1)都是齐次方程(9)的解, 并且是线性无关的. 由于方程(9)是k阶常系数齐次线性差分方程,满足可加性,所以这些线性无关解的线性组合便是含k个参数的通解.(获证) 定理3.3 齐次方程 xn+2-2axn+1+(a2+b2)xn=0 的通解为 (15) (16) 证明易知μ1=a+bi,μ2=a-bi 为方程的共轭复根,故齐次方程 xn+2-2axn+1+(a2+b2)xn=0 的通解可写成 令 则rncos(nθ)与rnsin(nθ)是两个线性无关的实离散函数,通解可以表示为两者的线性组合,即式(15)成立. 另一方面,齐次方程 xn+2-2axn+1+(a2+b2)xn=0 的通解也可写成 xn=c1(a+bi)n+c2(a-bi)n= c1an(1+hi)n+c2an(1-hi)n, 由二项公式 利用定义(见式(16)) 即得特征值为共轭复根时的通解的等价形式为 值得指出的是,尽管通解有两种形式,后面将发现:在确定非齐次差分方程的特解时,使用第二种形式(即拟初等函数形式)会给计算带来方便. 例6)求差分方程 xn+2-5xn+1+6xn=0 的通解. 解:对应特征方程为 μ2-5μ+6=0, 解得 μ1=2, μ2=3≠μ1. 由定理3.1知通解为 例7)求差分方程 xn+2+6xn+1+9xn=0 的通解. 解:对应特征方程为 μ2+6μ+9=0, 解得 μ1=μ2=-3. 由定理3.2知通解为 xn=c1(-3)n+c2n(-3)n= 例8)求差分方程 xn+2-2xn+1+2xn=0 的通解. 解:对应特征方程为 μ2-2μ+2=0, 解得 μ1=1+i, μ2=1-i. a=b=1, 由定理3.3知通解为 即 例9)求差分方程 Δ4xn+Δ2xn=0 的通解. 解法1:差分算子对应的特征方程为 λ4+λ2=0. 即 λ2(λ2+1)=0. 解得 λ1=λ2=0, λ3=i, λ4=-i. 于是方程的通解为 xn=(c1+c2n)(1+0)n+ A3(1+i)n+A4(1-i)n= 解法2:差分方程Δ4xn+Δ2xn=0可以分两种情况: 或者 Δ2xn=0,此时更有 Δ4xn=0.可见 Δ2xn=0的解都是原方程的解.利用差分的逆运算“和分”[4]可得 xn=Δ-2(0)=P<2(n)=c1+c2n. 或者Δ2xn≠0,此时必有Δ2xn+xn=0. 可见Δ2xn=-xn的解也是原方程的解.考虑到拟初等函数满足[1] Δ2cos!(n)=-cos!(n), Δ2sin!(n)=- sin!(n), 可知cos!(n)与 sin!(n)是方程Δ2xn=-xn的两个线性无关解.于是方程Δ2xn=-xn的通解为 最后得到原方程的通解为 xn=c1+c2n+c3cos!(n)+c4sin!(n)= 其中 (17) [1]孙建新.拟初等函数的差分性质及其应用[J].绍兴文理学院学报,2015,35(9):31-36. [2]孙建新.函数展开为阶乘幂级数的方法[J].绍兴文理学院学报,2016,36(7):29-34. [3]孙建新,胡金杰.阶乘幂的差分算子及其逆[J].绍兴文理学院学报,2005,25(7):22-25. [4]孙建新.阶乘幂多项式及其基本恒等式[J].绍兴文理学院学报,2004,24(7):34-37. [5]孙建新.stirling数的一个计算公式[J].绍兴师专学报,1986(2):46-51.