FDM工艺缝隙模型及消除方法研究

赵 庆 红， 郭 俊 卿*， 陈 拂 晓， 张 信 民

( 1.河南科技大学 材料科学与工程学院， 河南 洛阳 471023；2.有色金属共性技术河南省协同创新中心， 河南 洛阳 471023；3.洛阳天久铝业有限公司， 河南 洛阳 471023 )

0 引 言

熔融沉积成型(fused deposition modeling，简称FDM)技术利用热塑性材料的热熔性、黏结性等特点，在计算机控制下进行层层堆积叠加，最终形成所需产品或模型[1]．FDM快速成型技术无需激光系统，因而使用及维护简单，运行费用低、可靠性高，在三维实体模型制造等领域得到了越来越广泛的应用[1-2]．FDM制件的质量与工艺参数联系紧密．单独采用轮廓偏置线作为填充路径所得制件中易出现一个沿Z方向的稀疏带，对制件的物理性能造成不利影响，奇数层与偶数层采用不同路径填充可以改善制件质量[3]．Zhang等[4]基于鲁棒设计原理进行FDM工艺参数优化，指出路径宽度对制件质量的影响大于挤出速度、填充速度和层厚．Kaveh等[5]研究了工艺参数对HIPS(high impact polystyrene，高抗冲聚苯乙烯)材料成型质量的影响，指出路径宽度较小时易产生填充不足，路径宽度较大时易过度堆积造成重叠．不同层厚对应的最佳路径宽度不同，层厚为0.25 mm路径宽度取0.605 mm时所得制件质量较理想．层厚较大时，制件表面产生的台阶高度较大、台阶痕迹明显，表面质量和精度较差；反之，制件表面质量较好，但需要加工的层数增多，加工效率降低[6-10]．Lee等[11]应用FDM工艺制作ABS材质的玩具弹弩，通过测验指出光栅角度为30°/60°时弹弩的射程最远，但缺乏光栅角度对产品表面质量影响的研究．本文主要针对FDM成型工艺中产生的缝隙建立数学模型，并将模型计算与实验结果进行对比分析．

1 缝隙分析与熔合模型的建立

1.1 成型平面路径与缝隙

FDM工艺是通过热熔丝料沉积成型，路径宽度和光栅角度是对成型质量有重要影响的工艺参数．路径宽度是指热熔丝料进行堆积时每道丝料的设定宽度，光栅角度是指X-Y平面内热熔丝料堆积路径方向与成型室内X轴正方向的夹角，如图1所示．

由于丝料具有一定的宽度且是熔融态，按照设定路径进行连续填充时，虽然拐折处是尖角路径但实际填充效果呈圆弧状，不能完全与周围的丝料相熔合，从而导致外部轮廓线与内部光栅线熔合处出现一定缝隙，路径宽度和光栅角度是影响缝隙大小的主要因素．

图1 FDM工艺X-Y成型平面上填充路径

1.2 缝隙熔合模型的建立

根据X-Y平面内丝料填充方式及外部轮廓线与内部光栅线之间的熔合情况，建立缝隙熔合模型．

光栅角度θ=0°时，光栅线与轮廓线相互平行，其熔合效果主要受到路径宽度的影响：路径宽度W能够被制件Y方向的尺寸整除时，熔合效果最佳，无缝隙；若路径宽度W不能被制件Y方向的尺寸整除，易出现缝隙．设Y/W的余数为R，内部光栅线以制件X-Y平面的中心为参考中心，将缝隙均分给对称的两边，则光栅线与轮廓线之间的缝隙宽度为R/2．R越小熔合效果越佳．

光栅角度θ∈(0°，90°]时，光栅线与轮廓线之间的熔合形态如图2所示．图中阴影部分即为光栅线与轮廓线之间产生的熔合缝隙．

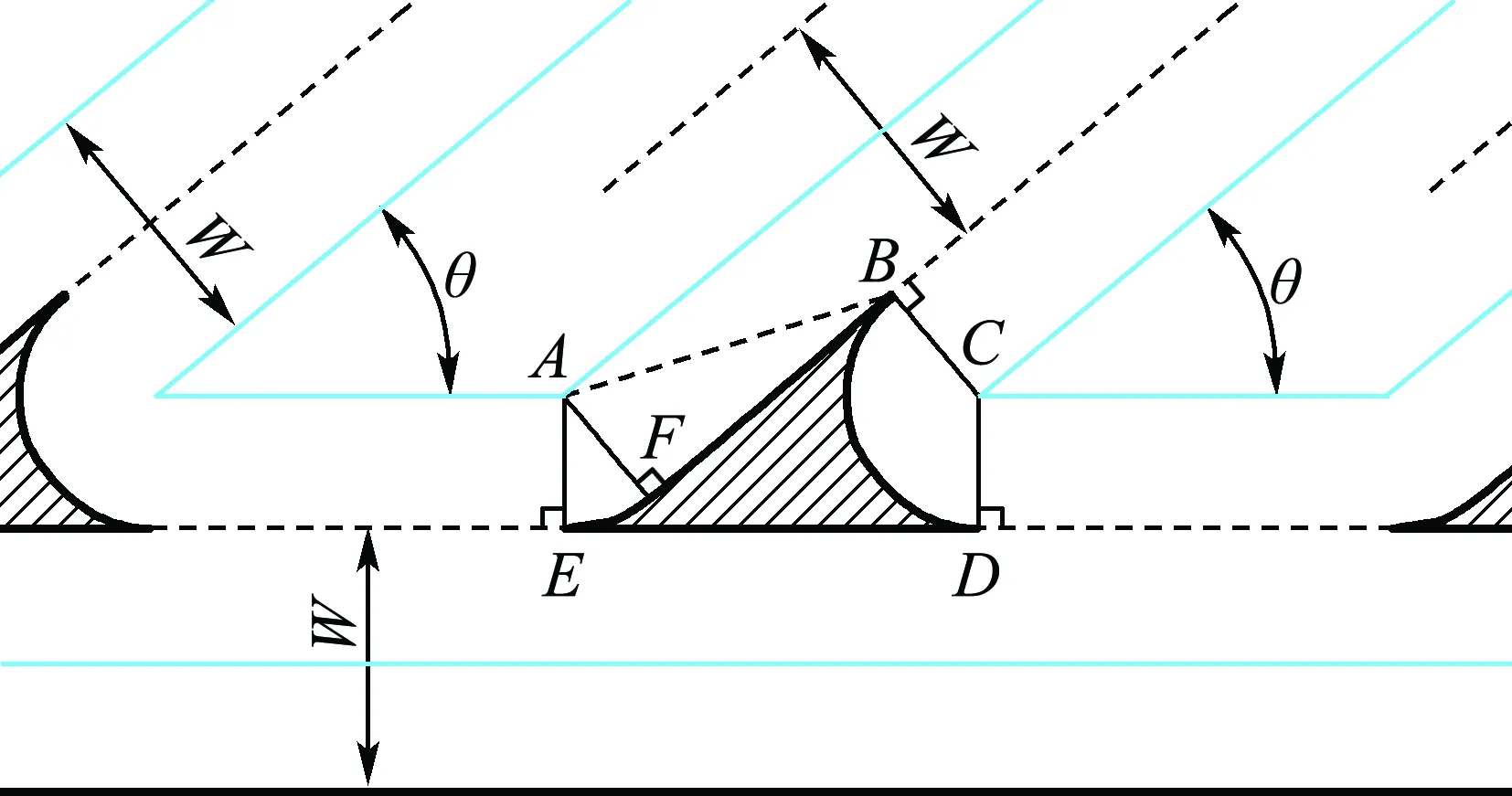
图2 θ∈(0°,90°]时缝隙熔合模型

缝隙面积

Sgap=S0-(S1+S2+S3)

(1)

由此可知θ∈(0°，90°]时，光栅线与轮廓线之间的缝隙面积为

(2)

其中θ=90°时，S1=0，光栅线与轮廓线之间的熔合形态如图3所示，阴影部分面积为

(3)

图3 θ=90°时缝隙熔合形态

2 实验方案

本实验以路径宽度和光栅角度为因素，实验因素与水平表如表1所示．实验设备为美国Stratasys公司的Fortus-360MC快速成型机，填充路径采用单圈光栅线与轮廓线相结合，奇数层与偶数层光栅线方向垂直．制件尺寸为15 mm×15 mm×15 mm，为兼顾制件表面质量与成型效率，层厚取0.254 mm．

制件后处理方法：在25%的NaOH水溶液中经超声波清洗1 h溶解底座支撑材料后，用蒸馏水洗涤去除残余NaOH，最终将制件置于75 ℃干燥箱中烘干2 h．

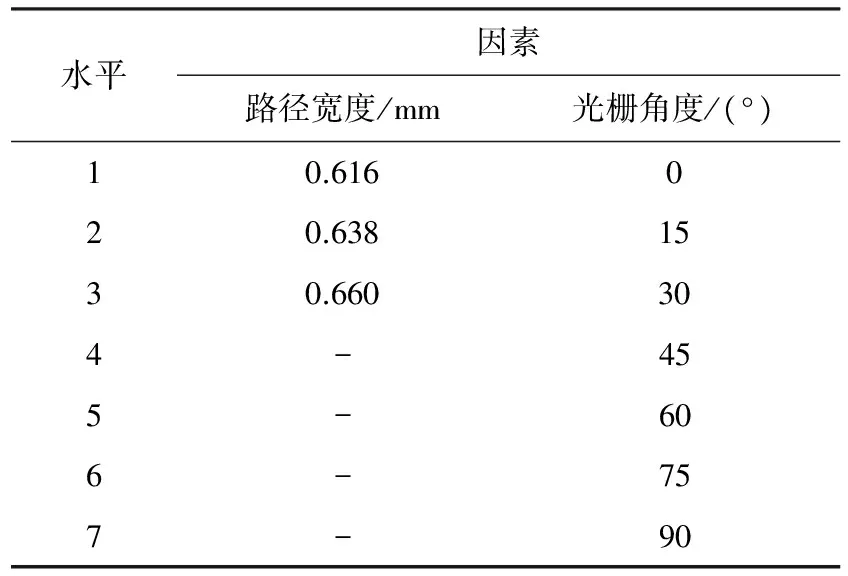
表1 实验因素与水平表

选取制件上表面边长中段，利用OLYMPUS显微镜对缝隙进行5次测量，将所得数据剔除最大值和最小值后取平均值．对于光栅角度θ=0°的制件，测量缝隙宽度误差范围为±0.006 mm；光栅角度θ∈(0°，90°]时，测量缝隙面积误差范围为-0.004～0.003 mm2．

3 结果与讨论

光栅角度θ=0°时，若路径宽度不能被制件Y方向的尺寸整除，模型缝隙宽度等于R/2．路径宽度为0.616、0.638、0.660 mm时，R/2分别为0.175、0.255、0.364 mm．光栅线与轮廓线之间的实际熔合情况如图4所示．由于丝料冷却固化时受到下面一层材料和周围材料的影响收缩不均匀，同一制件同一条缝隙各处的宽度有轻微波动．图4(a)～(c)中缝隙平均宽度分别为0.145、0.227、0.341 mm，图4(a)中熔合缝隙最窄，(b)次之，(c)最宽．实验结果与模型预测规律一致：R较小时熔合效果较好，R增大缝隙也由窄变宽．

图4 θ=0°时，光栅线与轮廓线之间实际缝隙

光栅角度θ∈(0°，90°]时，模型计算值与实验测量的缝隙面积对比图如图5所示，以θ=30°为例，W=0.616 mm，0.638 mm，0.660 mm时的模型缝隙面积分别为0.230、0.247、0.265 mm2，实际测量值分别为0.201、0.236、0.243 mm2，实际缝隙小于模型缝隙，缝隙随着路径宽度增大而增大．以W=0.638 mm时为例，随着光栅角度增大缝隙面积减小，且减小的趋势变缓．实际缝隙面积与模型预测面积变化规律一致，光栅线与轮廓线之间的缝隙面积随着光栅角度增大而减小，θ=90°时缝隙面积最小．实际缝隙面积略小于模型缝隙面积，这是因为实际填充时光栅线与轮廓线路径平行处、光栅线路径拐折处丝料扩散熔合使微小角隙得到了填充．图6中(a)～(f)分别为光栅角度θ=15°，30°，45°，60°，75°，90°时的实际熔合缝隙．

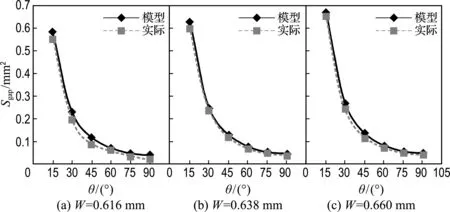
图5 模型与实际缝隙面积对比

图6 光栅线与轮廓线之间实际缝隙(W=0.660 mm)

制件中光栅线与轮廓线之间的缝隙有线状和孔状两种形态．θ=0°与θ=90°时获得的制件，两条对边的缝隙为线状、另两条对边的缝隙为孔状．θ∈(0°，90°)时，4条边上都是孔状缝隙．通过改善熔合状况可以消除线状缝隙，而孔状缝隙只能减小无法消除．

相同路径宽度，θ=0°与θ=90°时获得的制件相同．W=0.616 mm，θ=0°与θ=90°时所得制件的光栅线与轮廓线之间熔合效果较好、缝隙较小．对于X、Y方向尺寸相同(X=Y)的制件，选择能被制件Y方向尺寸整除的较小路径宽度、θ=0°或90°，获得的制件光栅线与轮廓线之间熔合效果好，两条对边无缝隙、另两条对边孔状缝隙小．若X>Y，选择能被制件Y方向尺寸整除的较小路径宽度、θ=0°，能够获得两条长对边无缝隙、另两条短对边孔状缝隙很小的制件；反之，选择能被制件X方向尺寸整除的较小路径宽度、θ=90°．

当实际所需光栅角度θ∈(0°，90°)时，所得制件中光栅线与轮廓线之间的缝隙形态为孔状，可以结合实际设计较小的光栅角度和路径宽度来减小缝隙．或者尝试在光栅线与轮廓线熔合处减小光栅线的填充速度、增大填充材料量使孔状缝隙减小，但该设备不具备条件．

4 结 论

(1)光栅角度θ=0°或90°时，光栅线与轮廓线之间会出现线状缝隙，线状缝隙大小与路径宽度W有关：制件Y方向尺寸除以路径宽度所得余数R越小，熔合效果越好、线状缝隙宽度越小．对于确定的路径宽度W，θ=0°或90°时，孔状缝隙最小．

(2)当光栅角度θ为(0°，90°)的一个确定值时，光栅线与轮廓线之间只有孔状缝隙，孔状缝隙面积随着路径宽度W增大而增大，且增大速度变快．若路径宽度W为确定值，光栅角度θ∈(0°，90°)时，θ越大，则光栅线与轮廓线之间的孔状缝隙越小，且减小趋势变缓．

(3)为获得无线状缝隙且孔状缝隙很小的制件，应让线状缝隙出现在制件的长边上、孔状缝隙出现在短边上，路径宽度设置为可以被短边尺寸整除的较小值．在光栅线与轮廓线拐折熔合处减小光栅线的填充速度、增大填充材料量或许有利于减小孔状缝隙，但该设备不具备条件，应根据快速成型设备及程序等展开进一步研究．

[1] 韩 霞,杨恩源. 快速成型技术与应用[M]. 北京:机械工业出版社, 2012:47.

HAN Xia, YANG Enyuan.RapidPrototypingTechnologyandApplication[M]. Beijing: China Machine Press, 2012:47. (in Chinese)

[2] 王广春,赵国群. 快速成型与快速模具制造技术及其应用[M]. 3版. 北京:机械工业出版社, 2013:91.

WANG Guangchun, ZHAO Guoqun.RapidPrototypingandRapidToolingManufacturingTechnologyandApplications[M]. 3rd ed. Beijing: China Machine Press, 2013:91. (in Chinese)

[3] 范丽荣,任 翀,曹一青. FDM工艺快速成型技术中均匀壁厚截面填充路径的优化[J]. 中国制造业信息化, 2011,40(11):39-41.

FAN Lirong, REN Chong, CAO Yiqing. Filling path optimization of consistent thickness in FDM rapid prototyping technology [J].MachineDesignandManufacturingEngineering, 2011,40(11):39-41. (in Chinese)

[4] ZHANG Jianfeng, PENG Anhua. Processing parameter optimization of FDM based on robust design [J].TransactionsofNanjingUniversityofAeronautics&Astronautics, 2012,29(1):62-67.

[5] KAVEH M, BADROSSAMAY M, FOROOZMEHR E,etal. Optimization of the printing parameters affecting dimensional accuracy and internal cavity for HIPS material used in fused deposition modeling processes [J].JournalofMaterialsProcessingTechnology, 2015,226:280-286.

[6] BOSCHETTO A, GIORDANO V, VENIALI F. 3D roughness profile model in fused deposition modelling [J].RapidPrototypingJournal, 2013,19(4):240-252.

[7] MOHAMED O A, MASOOD S H, BHOWMIK J L. Optimization of fused deposition modeling process parameters for dimensional accuracy using I-optimality criterion [J].Measurement:JournaloftheInternationalMeasurementConfederation, 2016,81:174-196.

[8] 邹国林,郭东明,贾振元,等. 熔融沉积制造工艺参数的优化[J]. 大连理工大学学报, 2002,42(4):446-450.

ZOU Guolin, GUO Dongming, JIA Zhenyuan,etal. Research on process parameter optimization of fused deposition modeling [J].JournalofDalianUniversityofTechnology, 2002,42(4):446-450. (in Chinese)

[9] 黄 丹,张效迅,习 武,等. 基于FDM工艺的打印件成型时间与力学性能的研究[J]. 塑料工业, 2016,44(3):89-93.

HUANG Dan, ZHANG Xiaoxun, XI Wu,etal. The research of the printing time and mechanical properties of the printout based on FDM process [J].ChinaPlasticsIndustry, 2016,44(3):89-93. (in Chinese)

[10] 彭安华,张剑峰,张江林. FDM工艺参数对制件精度影响的实验研究[J]. 淮海工学院学报(自然科学版), 2008,17(1):21-24.

PENG Anhua, ZHANG Jianfeng, ZHANG Jianglin. Experimental research into the influence of technical parameters on parts precision [J].JournalofHuaihaiInstituteofTechnology(NaturalSciencesEdition), 2008,17(1):21-24. (in Chinese)

[11] LEE B H, ABDULLAH J, KHAN Z A. Optimization of rapid prototyping parameters for production of flexible ABS object [J].JournalofMaterialsProcessingTechnology, 2005,169:54-61.