基于最优化瞬心线的纯滚剪切机构设计

刘 彪， 马 雅 丽， 王 德 伦， 黎 康 康

( 大连理工大学 机械工程学院， 辽宁 大连 116024 )

0 引 言

两刚体间的纯滚运动在很多常用机械中有着广泛而重要的应用．通常采用机构实现纯滚运动，而机构设计的关键在于如何利用轨迹综合方法确定机构的尺寸[1-2]．机构轨迹综合问题以离散点或连续轨迹的方式给出，其实现方法分为精确点综合和近似综合[3]．在精确点综合难以实现的情况下可以使用近似综合．

一般来说，近似综合又分为直接综合和间接综合．直接综合法直接根据运动学原理求解机构方案，如Hrones[4]使用连杆曲线集分析四杆机构，Kramer[5]使用Hooke-and-Jeeves搜索法，Subbian等[6]使用连续法处理多项式方程来实现四杆机构轨迹生成综合，但这些数值方法往往难以处理高阶非线性方程组．王德伦等[7]提出了自适应拟合方法和法向误差的鞍点规划模型用于四杆机构运动综合．为了同时保证有效性和高精度，许多优化算法也被用于机构轨迹综合，如遗传优化算法[8]、模拟退火法[9]等．间接综合法[10-11]是从预先建立的轨迹图谱中搜索匹配的轨迹，输出机构构型和尺寸，该方法依赖于海量数据存储容量和计算机快速检索能力．

纯滚剪切机构设计需要同时保证纯滚运动轨迹和剪切性能，如用于中厚钢板剪切的滚剪机，为保证剪切质量，理想剪切动作应保证上下剪刃作纯滚运动，没有滑移．现有方法往往选择保证若干关键点精确运动的方式完成设计，或对上剪刃动态最低点轨迹优化[12]，但非关键点处易出现较大的运动误差和水平滑移．因此，本文通过研究剪刃完整滚切运动的动、定瞬心线与接触线的对应关系，建立一种新型的以最优化瞬心线为基础的纯滚运动机构综合模型，以期获得最优化的机构尺寸，使得滚剪机在整个剪切过程中具有最小的运动误差和水平滑移量，提高剪切质量．

1 运动设计模型

刚体作相对运动时速度相同的点称为速度瞬时中心，简称速度瞬心或瞬心．瞬心在固定刚体平面内的轨迹称为定瞬心线，在运动刚体平面内的轨迹称为动瞬心线．纯滚运动意味着两个刚体间相对运动没有滑移，瞬时接触点相对速度为零．因此，只要动、定瞬心线分别符合刚体运动时的接触线，就可以保证两刚体做纯滚运动．

滚剪机的理想剪切运动应为上剪刃和下剪刃相对纯滚运动．本文选择二自由度连杆式滚剪机作为设计对象，其机构简图如图1所示[13]．以下推导该七连杆机构的瞬心线运动方程．

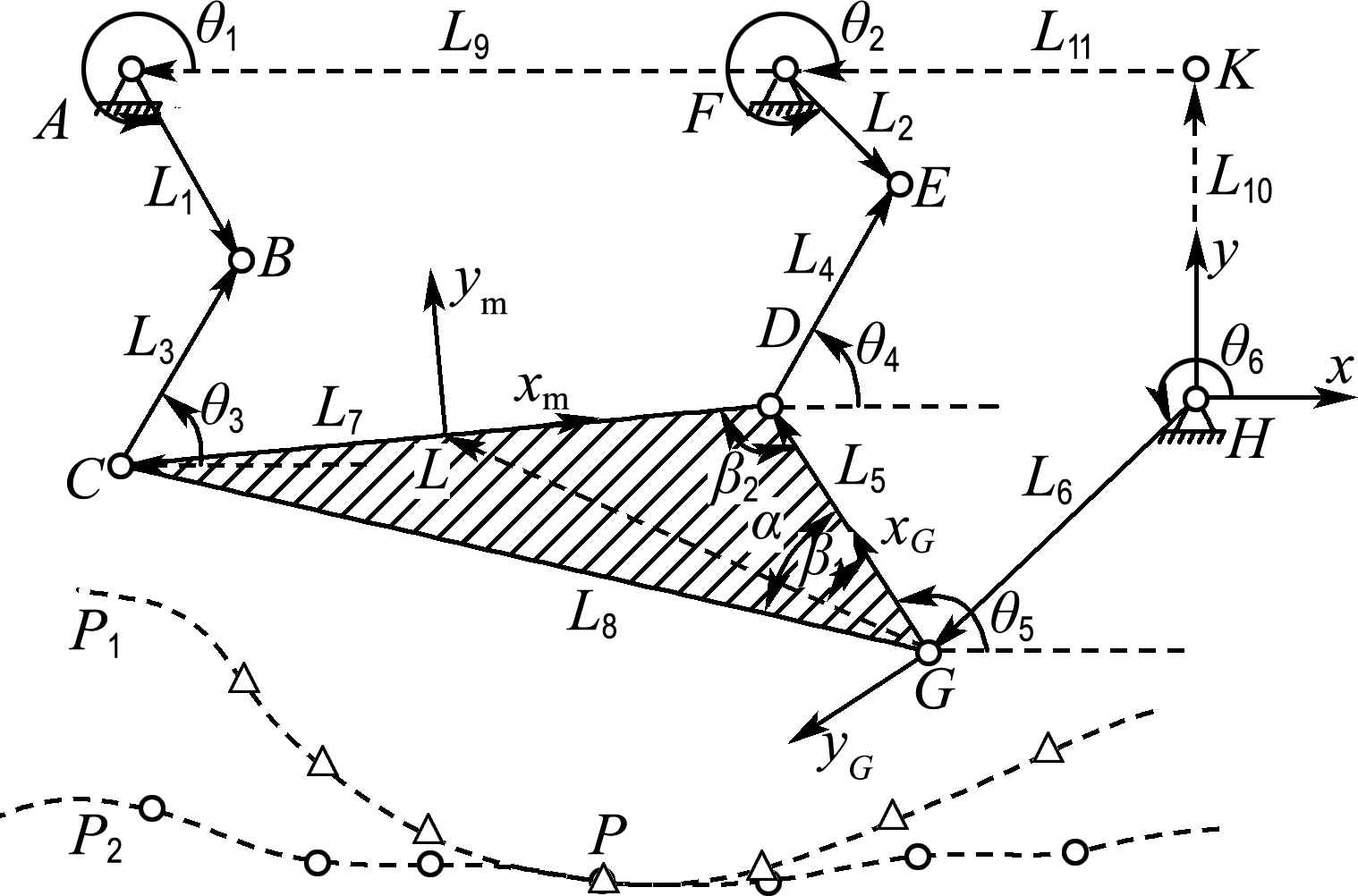
图1 七连杆机构简图

如图1所示，杆AB和EF是原动件，杆CDG是从动件作为执行机构．在定铰链点H处建立定坐标系H-xy，在杆CDG上的CD中点L处建立动坐标系L-xmym．各杆长度分别记为{Li，i=1，2，…，11}，各杆的相位角和角速度分别记为{θi，i=1，2，…，6}和{ωi，i=1，2，…，6}．对闭环HGDEFKH和闭环HGCBAFKH列闭环矢量方程：

HG+GD+DE=HK+KF+FE

(1)

HG+GC+CB=HK+KF+FA+AB

(2)

将式(1)和(2)投影在固定坐标系的两个坐标轴上，得

L6cosθ6+L5cosθ5+L4cosθ4+L11-

L2cosθ2=0；

L6sinθ6+L5sinθ5+L4sinθ4-L10-

L2sinθ2=0

(3)

L6cosθ6+L8cos(θ5+α)+L3cosθ3+L9+

L11-L1cosθ1=0；

L6sinθ6+L8sin(θ5+α)+L3sinθ3-L10-

L1sinθ1=0

(4)

该机构通过齿轮传动共用一个动力源，即原动件杆AB和EF做等速同向转动，二者相位差θ1-θ2=θC，其中θC为定值．由此可以确定式中各角度．

分别将方程组(3)、(4)对时间求导，得出速度方程组如下：

-L6ω6sinθ6-L5ω5sinθ5-L4ω4sinθ4+

L2ω2sinθ2=0；

L6ω6cosθ6+L5ω5cosθ5+L4ω4cosθ4-

L2ω2cosθ2=0

(5)

-L6ω6sinθ6-L8ω5sin(θ5+α)-L3ω3sinθ3+

L1ω1sinθ1=0；

L6ω6cosθ6+L8ω5cos(θ5+α)+L3ω3cosθ3-

L1ω1cosθ1=0

(6)

其中ω2=ω1为原动件的角速度．求解方程组(5)和(6)即可确定式中各角速度．理想的设计方案要求杆CDG在纯滚剪切过程中相对于机架产生纯滚运动．在整个纯滚剪切过程中，速度瞬心P相对于从动件CDG形成动瞬心线，相对于机架形成定瞬心线，分别对应图1中的曲线P1和P2．

为了便于定坐标系和动坐标系间的坐标变换，在杆CDG的运动平面上引入动坐标系G-xGyG．记速度瞬心P在定坐标系和动坐标系中的坐标分别为(x，y)和(xm，ym)，使用坐标变换矩阵将各点从动坐标系变换到定坐标系中，则两组坐标存在如下关系：

r=MHGMGLrm

(7)

其中r=(xy1)T，rm=(xmym1)T，MHG为坐标系H-xy与G-xGyG间的齐次坐标变换方程，MGL为坐标系G-xGyG与L-xmym间的齐次坐标变换方程，分别由下式给出：

(8)

式(8)中θ5与θ6分别为杆L5与L6的方位角．β1与β2分别为两坐标系的相对转角．记LGL为杆GL的杆长，将上式代入式(7)并对时间求导，可得

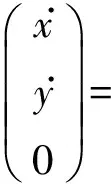
x．y．0æèçççöø÷÷÷=

(9)

xm=LGLω5cos(β1+β2)+

L6ω6cos(β2+θ6-θ5)；

ym=LGLω5sin(β1+β2)+

L6ω6sin(β2+θ6-θ5)

(10)

将式(10)代入式(7)，则可以得到定瞬心线方程：

x=LGL(ω5+1)cos(β1+θ5)+

L6(ω6+1)cosθ6；

y=LGL(ω5+1)sin(β1+θ5)+

L6(ω6+1)sinθ6

(11)

至此动瞬心线和定瞬心线都可以求解出来，在此基础上即可以搜索连杆机构的最优化尺寸和杆件角度，使得机构构件的动、定瞬心线以纯滚运动的方式配合运动．

2 优化设计实例

依据纯滚运动特性方程和剪切性能的相关要求建立最优化目标函数和约束条件，考虑到求解的有效性和便捷性，采用遗传算法[14]求解即可得到合适的滚剪机机构尺寸．以下以某钢厂七连杆式滚剪机的优化设计作为实例进行说明．

2.1 滚剪机剪刃参数

滚剪机的剪刃参数与剪切过程有关，这些参数包括剪切钢板宽度B、最大钢板厚度Tmax、剪切重叠量S和剪切角α，如图2所示．

图2 滚剪机剪刃参数

钢板宽度B确定下剪刃的宽度，剪切重叠量S确定剪切过程中上、下剪刃的重叠量，剪切角α是指下剪刃与圆弧上剪刃切线在接触点处的夹角．

2.2 优化模型

根据剪刃参数可以求得期望的上剪刃和下剪刃廓线．建立优化模型的目的即是在满足特定约束的条件下，获得一组最优化机构尺寸使得瞬心线与期望的上、下剪刃轨线之间具有最小的偏差．

(1)优化变量

滚剪机的设计变量一般包括杆长、杆方位角和铰链点位置，将这些设计变量作为优化变量，记为

t=(t1t2…tn)T，t∈Rn

(12)

其中的每一个元素ti(i=1，2，…，n)对应着机构的一个尺寸参数，如杆长Lj(j=1，2，…，11)和角度θk(k=1，2，…，6)等，最优设计方案可由结果向量t*表示，即最优点．

(2)优化目标函数

最优化设计的目标是使动瞬心线尽量逼近上剪刃廓线，同时定瞬心线尽量逼近下剪刃廓线．基于此，将目标函数定义为两对曲线的吻合误差和，即动瞬心线与上剪刃廓线的吻合误差加上定瞬心线与下剪刃廓线的吻合误差，由下式给出：

minU(t)
U(t)=U1(t)+U2(t)

(13)

其中U1(t)为动瞬心线与上剪刃廓线的吻合误差，U2(t)为定瞬心线与下剪刃廓线的吻合误差．分别在上剪刃平面和下剪刃平面上建立用于评估吻合误差的坐标系Om-xmym和O-xy，如图3和4所示．

图3 动瞬心线与圆弧上剪刃

图4 定瞬心线与水平下剪刃

坐标系Om-xmym固定在圆弧上剪刃平面上，随之转动，动瞬心线和上剪刃廓线表示为

ym=gmt(xm)
ym=fm(xm)；xm1≤xm≤xmn

(14)

坐标系O-xy固定在水平下剪刃平面上，相对机架固定，定瞬心线和下剪刃廓线表示为

y=gt(x)
y=f(x)=C；x1≤x≤xn

(15)

其中xn-x1=B，C是常数，对应着钢板剪切位置．

误差U1(t)和U2(t)由下式确定：

(16)

(17)

据此纯滚剪切机构设计的最优化目标函数可以表示为

(18)

(3)约束条件

滚剪机设计的约束条件主要是一些运动参数和剪切性能参数，包括开口度、上下剪刃的剪切重叠量误差和剪切力峰值．

①开口度约束

为了保证被剪钢板能够顺利通过，剪切结束后上下剪刃应能产生足够的间距，该间距称为上下剪刃间的开口度，记为J．开口度是设计变量的函数，应大于钢板的厚度T，即

J(t)≥T

(19)

②重叠量误差约束

为获得稳定的剪切质量，剪刃在板宽方向的重叠量应限制在一定范围．该值由上剪刃动态最低点k与下剪刃的距离确定，如图5所示．k点在定坐标系中的坐标由下式给出：

xk=xh-Rsinβ
yk=yh-R(1-cosβ)

(20)

其中R和β分别为上剪刃的圆弧半径和倾角；(xh，yh)为上剪刃圆弧中点h在定坐标系中的坐标．据此可得重叠量误差约束

|ΔS|=|C-yk-S|≤0.1S

(21)

其中S为理论重叠量．

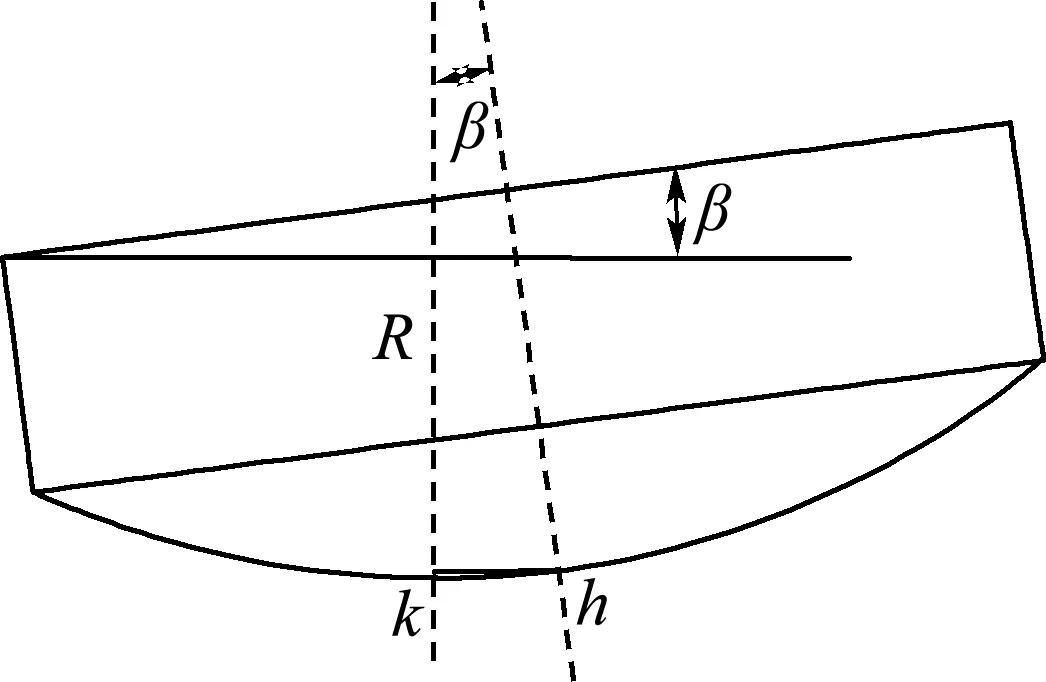
图5 上剪刃动态最低点k与剪刃圆弧中点h

③剪切力峰值约束

上剪刃的受力主要包含剪切力和摩擦力等，为保护剪刃，引入剪切力峰值约束以限制通常出现在初始剪切阶段的最大剪切力．滚剪机的剪切力[15]可由下式求得：

(22)

其中T为钢板厚度，σb和δ为钢板材料的强度极限和延伸率，Z为转换系数，r1为剪刃间隙与板厚之比，r2为剪刃下侧到钢板距离与板厚之比．上式表明剪切力约束可通过对剪切角α的处理实现，因此可将极限剪切角限定在指定的剪切角α0以上，即

αst≥α0

(23)

其中αst为上剪刃初始剪切角，由上剪刃圆弧与被剪钢板位置的几何关系所确定，即

(24)

其中(xo，yo)和(xq，yq)分别为上剪刃圆弧的圆心和钢板上表面初始剪切接触点在固定坐标系中的坐标．

通过求解上述滚剪机尺寸优化模型即可得到一组最优解t*，对应着满足上下剪刃间纯滚运动要求的最佳机构尺寸．由于模型的目标函数一般为多峰、非线性的，故本文采用遗传算法来求解该优化问题．

3 结果与分析

3.1 优化结果

以某钢厂七连杆式滚剪机作为设计实例，如图6所示．滚剪机的原始机构尺寸为AB=EF=115 mm，BC=ED=865 mm，AF=CD=2 400 mm，DG=862 mm，HG=800 mm，F点坐标为(-1 624，988)．使用真实的钢板剪切剪刃参数进行设计，如表1所示．

图6 滚剪机机构示意图

表1 滚剪机的剪刃参数

使用各杆杆长和两曲柄的初始相位角作为优化变量，将式(15)中的常数C设定为-400 mm，选择初始剪切角约束为αst≥1.5°．建立滚剪机优化模型并使用遗传算法求解，即可得到新的机构尺寸设计结果，最后设计出的滚剪机机构尺寸为AB=EF=115 mm，BC=ED=864 mm，AF=CD=2 400 mm，DG=856.68 mm，HG=807 mm，固定铰链F点坐标为(-1 638，1 033)；杆AB的初始相位角为113.8°．

3.2 运动与性能分析

优化结果最重要的运动性能是保证滚剪机上、下剪刃间的纯滚运动，即动瞬心线和定瞬心线和上、下剪刃廓线之间具有最小的偏差，通常使用圆弧上剪刃的动态最低点迹线和上剪刃水平滑移量作为评价指标[12]．剪切性能一般使用剪切角和剪切力作为新旧设计结果的评价指标．

图7分别为新旧两种设计方案的定瞬心线与水平下剪刃廓线．优化设计后的定瞬心线相比原方案在剪切阶段具有更好的直线度，即能更好地逼近下剪刃廓线．

图8分别为新旧两种设计方案的动瞬心线与圆弧上剪刃廓线．新设计方案的动瞬心线近似于对称的圆弧，这意味着动瞬心线能够更好地逼近上剪刃的圆弧形廓线，这与滚剪机优化模型中的目标函数是一致的．

(a) 原方案

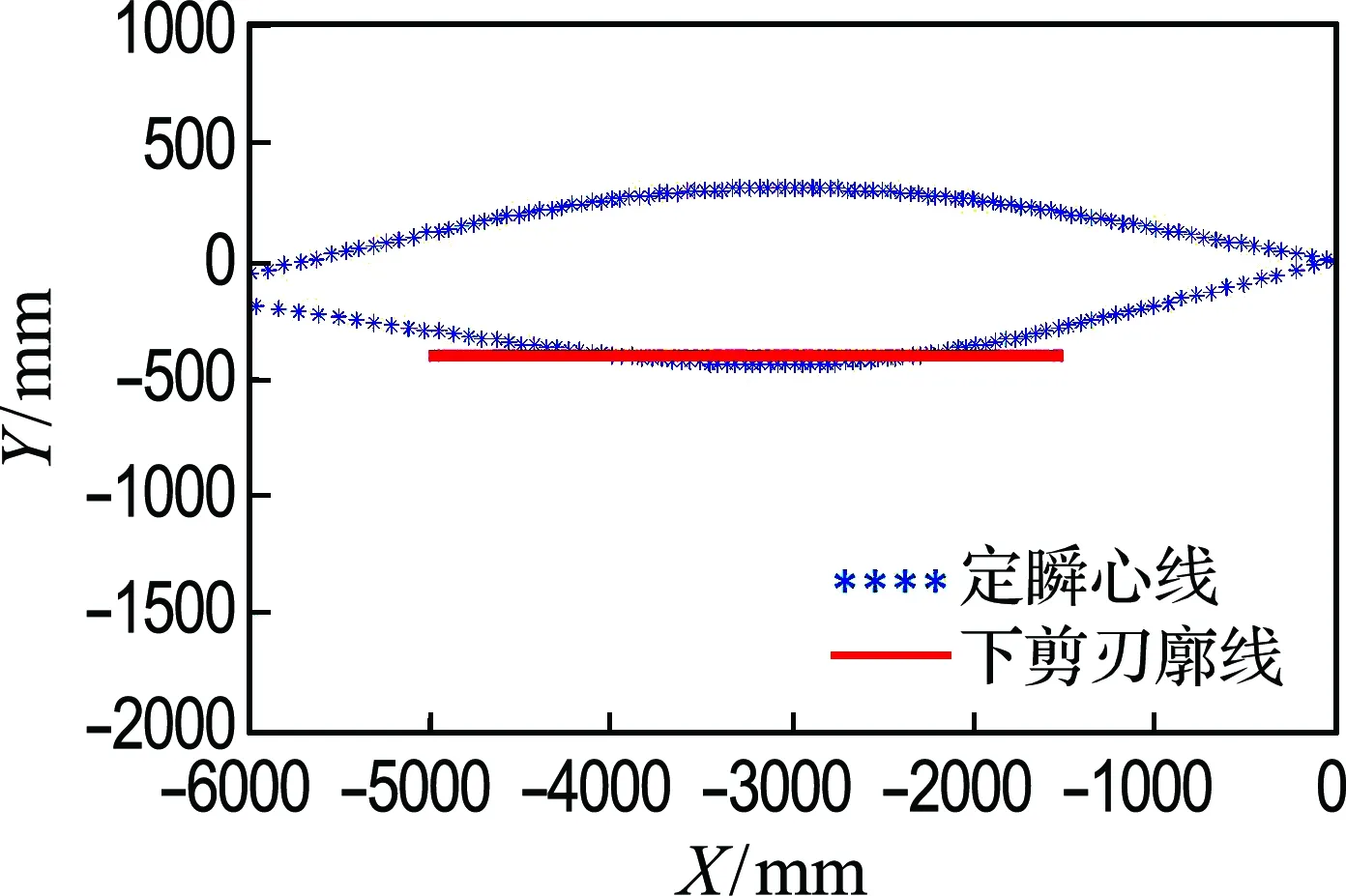
(b) 新设计方案

图7 定瞬心线与水平下剪刃廓线

(a) 原方案

(b) 新设计方案

图8 动瞬心线与圆弧上剪刃廓线

Fig.8 Moving centrode and lines of upper arc shear blade

图9和10分别为上剪刃圆弧中点在完整工作周期和剪切阶段的迹线．可以看出，新设计方案上剪刃在钢板剪切过程中的水平滑移量明显小于原方案，上剪刃更接近纯滚运动．

图11为上剪刃动态最低点集合的迹线，在钢板剪切阶段该迹线近似为一条直线，其直线度反映了上、下剪刃重叠量的均匀性．原方案的圆弧上剪刃动态最低点在剪切阶段的迹线点集标准差为1.890 mm，优化设计后该值变为0.352 mm，降低了81.4%，使得设计后的上、下剪刃重叠量更加均匀，也意味着更好的钢板剪切质量．

(a) 原方案

(b) 新设计方案

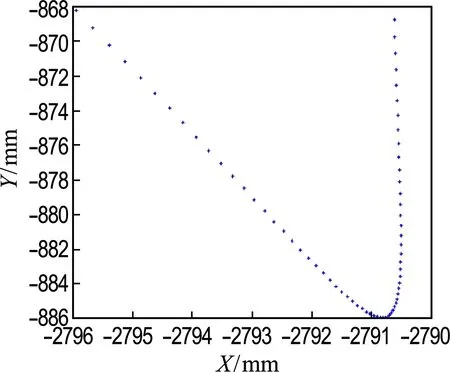
(a) 原方案

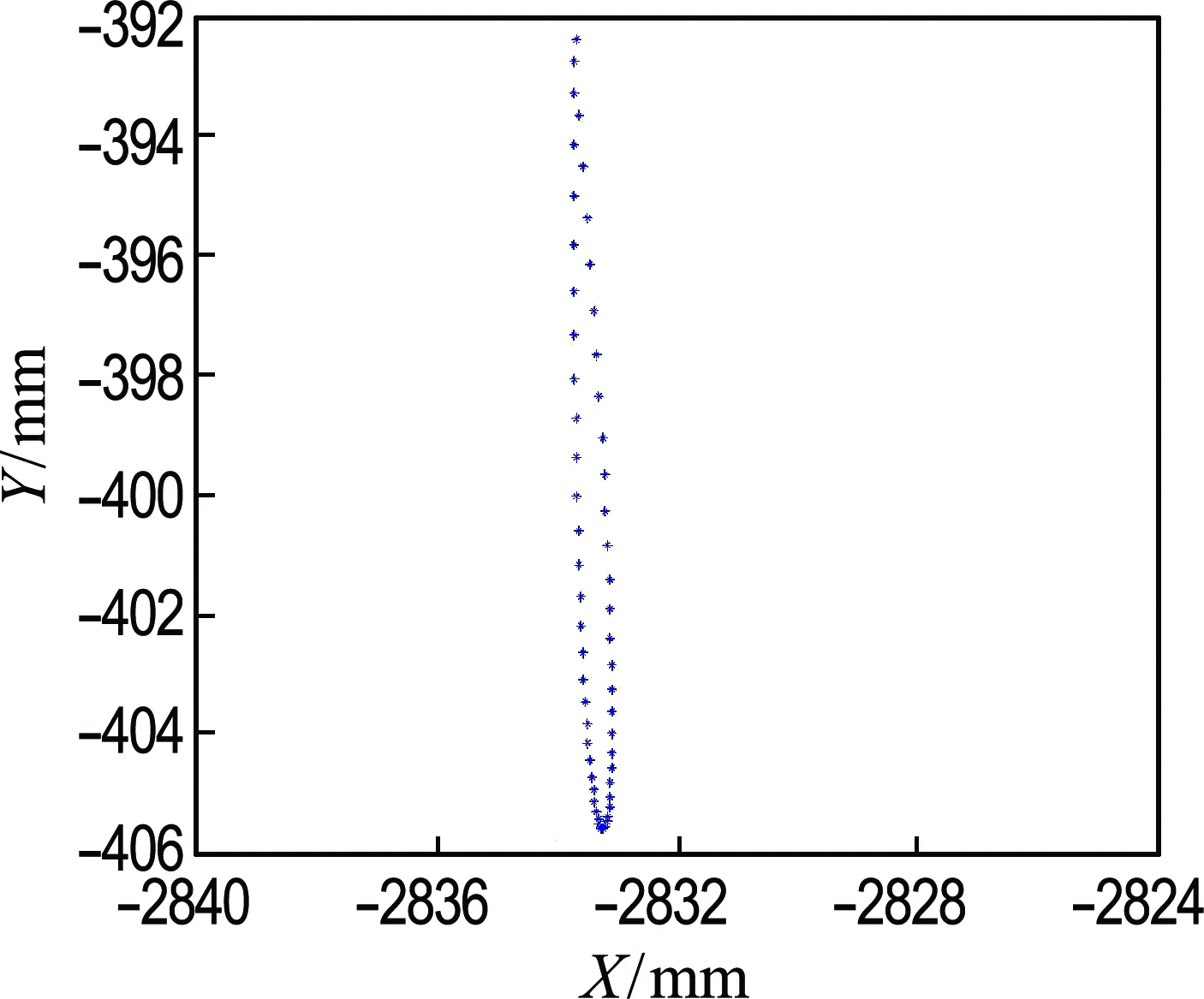
(b) 新设计方案

(a) 原方案

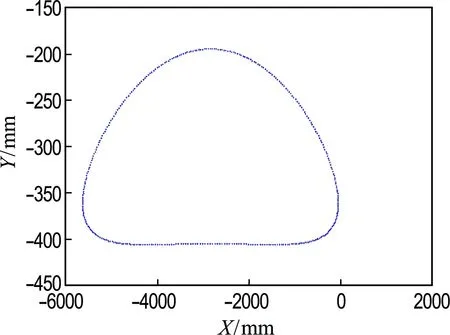
(b) 新设计方案

图12为设计前后剪切角和剪切力在钢板剪切过程中的变化曲线．原方案的初始剪切角为0.9°，其后剪切角大致稳定在2.2°左右；新设计方案的滚剪机初始剪切角变为约1.5°．初始剪切角的变化带来了剪切力峰值的改善，原方案的剪切力峰值为1.7×107N，优化设计后该值为1.2×107N，降低了约29.4%．从图中也可以看出，剪切力峰值大致与剪切角成反比关系，因此可以采用提高剪切角的方法降低剪切力峰值．

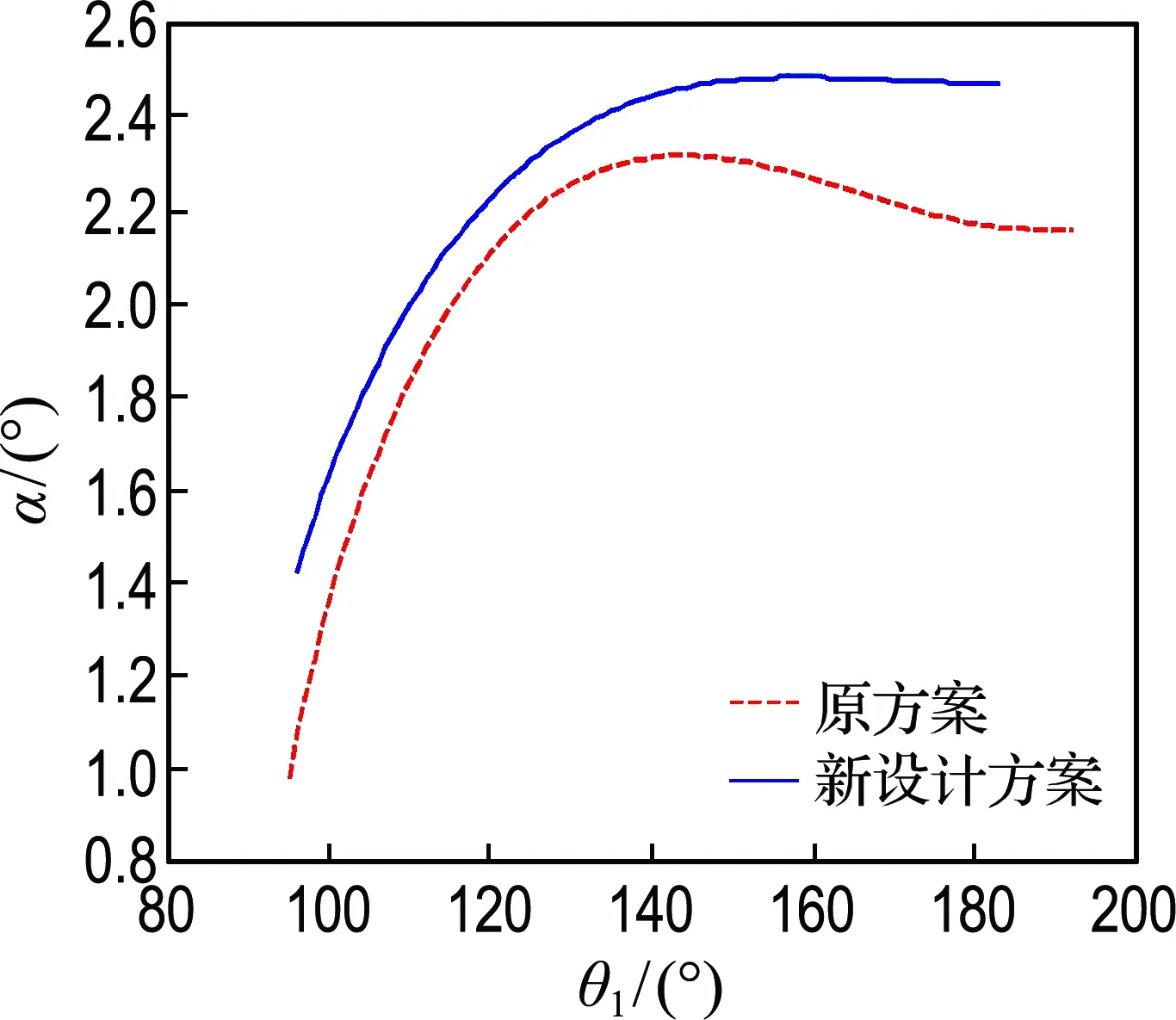
(a) 剪切角

(b) 剪切力

图12 设计前后的剪切角与剪切力对比

Fig.12 Comparison of shear angle and stress before and after the design

4 结 语

本文提出一种基于瞬心线优化的纯滚剪切机构的设计新方法，通过使用遗传优化算法求解模型即可得到一组最优化机构尺寸，使得机构瞬心线与纯滚动接触线的误差最小化．该方法应用于某钢厂的七连杆式滚剪机设计，与原方案相比：

(1)新设计方案的上剪刃动态最低点迹线点集标准差降低了81.4%，使得设计后的上、下剪刃重叠量更加均匀，从而获得了更好的钢板剪切质量．

(2)新设计方案的上剪刃水平滑移量明显低于原方案，有利于减少上剪刃磨损，提升剪切效率和剪板质量．

(3)新设计方案的剪切力峰值相比原方案降低了约29.4%，这有利于提高滚剪机的动力性能，延长使用寿命．

本文所提出的设计模型和方法不仅适用于七杆式纯滚剪切机构设计，而且可以扩展到其他类型的连杆式纯滚机构设计中．此外，在后续研究中也可以选择不同的优化求解方法以获得更好的计算结果．

[1] FIGLIOLINI G, ANGELES J. Synthesis of conjugate Geneva mechanisms with curved slots [J].MechanismandMachineTheory, 2002,37(10):1043-1061.

[2] WU Limei, REN Jing, YIN Tubang. Optimal design of rolling shear mechanism based on improved genetic algorithms [C] //Proceedings—2010InternationalConferenceonDigitalManufacturingandAutomation,ICDMA2010. Piscataway: IEEE Computer Society, 2010:68-71.

[3] BAI Shaoping, WANG Delun, DONG Huimin. A unified formulation for dimensional synthesis of Stephenson linkages [J].JournalofMechanismsandRobotics, 2016,8(4):041009.

[4] HRONES J A.AnalysisoftheFour-BarLinkage[M]. New York:Technology Press of the Massachusetts Institute of Technology, and Wiley, 1951.

[5] KRAMER S N. Selective precision synthesis of the four-bar motion generator with prescribed input timing [J].JournalofMechanicalDesign, 1979,101(4):614-618.

[6] SUBBIAN T, FLUGRAD D R. Four-bar path generation synthesis by a continuation method [J].JournalofMechanicalDesign, 1991,113(1):63-69.

[7] 王德伦,王淑芬,李 涛. 平面四杆机构近似运动综合的自适应方法[J]. 机械工程学报, 2001,37(12):21-26.

WANG Delun, WANG Shufen, LI Tao. New approach for mechanisms synthesis by adaptive saddle fitting [J].ChineseJournalofMechanicalEngineering, 2001,37(12):21-26. (in Chinese)

[8] CABRERA J A, SIMON A, PRADO M. Optimal synthesis of mechanisms with genetic algorithms [J].MechanismandMachineTheory, 2002,37(10):1165-1177.

[9] JOHNSON D S, ARAGON C R, MCGEOCH L A,etal. Optimization by simulated annealing:an experimental evaluation; Part II, Graph coloring and number partitioning [J].OperationsResearch, 1991,39(3):378-406.

[10] 李 震,桂长林. 连杆曲线特征分析的数学形态学方法[J]. 机械工程学报, 2002,38(2):27-30.

LI Zhen, GUI Changlin. Morphologically analyzing method for the characteristics of coupler curves of linkage mechanism [J].ChineseJournalofMechanicalEngineering, 2002,38(2):27-30. (in Chinese)

[11] 孙晓斌,肖人彬,王 雪. 基于曲线几何特征量化提取的轨迹机构检索生成方法[J]. 机械工程学报, 2000,36(11):98-105.

SUN Xiaobin, XIAO Renbin, WANG Xue. New approach to rapid searching path generating mechanisms [J].ChineseJournalofMechanicalEngineering, 2000,36(11):98-105. (in Chinese)

[12] 孙复森,杨惠新,闫晓强,等. 滚切式定尺剪机构参数优化研究[J]. 冶金设备, 2008(4):18-21.

SUN Fusen, YANG Huixin, YAN Xiaoqiang,etal. Simulation research of mechanism parameter on cut-to-length rolling shear [J].MetallurgicalEquipment, 2008(4):18-21. (in Chinese)

[13] 黎康康. 基于纯滚运动的滚切剪机构设计方法研究[D]. 大连:大连理工大学, 2009.

LI Kangkang. Research on the design method of rolling shear mechanism based on pure rolling [D]. Dalian: Dalian University of Technology, 2009. (in Chinese)

[14] 林晓辉,黄 卫,林晓通,等. 平面连杆变幅机构轨迹综合遗传退火优化算法的研究[J]. 计算机辅助设计与图形学学报, 2001,13(8):724-729.

LIN Xiaohui, HUANG Wei, LIN Xiaotong,etal. Study of synthetical genetics annealing optimization for the luffing mechanism locus of a plane link [J].JournalofComputer-AidedDesign&ComputerGraphics, 2001,13(8):724-729. (in Chinese)

[15] 温明军,王 芳. 滚切剪的剪切力计算[J]. 冶金设备, 2011(z1):1-3.

WEN Mingjun, WANG Fang. Sheared force calculation on the rotary cut shear [J].MetallurgicalEquipment, 2011(z1):1-3. (in Chinese)