基于流动理论的板材多步成形模拟方法
2018-01-19张向奎,刘伟杰,胡平
张 向 奎, 刘 伟 杰, 胡 平
( 大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024 )
0 引 言
经济发展和环境保护日益增长的需求,使得生产更加轻量化、几何形状复杂和低消耗费用的车用机械零件变得日益迫切.通过冷热冲压工艺得到的大尺寸的金属零件往往经历了多轴加载、高应变率和高温等复杂的加载条件.基于有限元的数值模拟方法可以对设计的零件提供零件成形性分析、起皱和破裂等缺陷估计,以辅助零件制造和优化工艺参数.
多步成形模拟有限元方法,通过快速构造若干的中间构型,基于流动理论的本构积分模型,以克服采用全量理论的一步法对最终零件的应力估计精度不足的问题.其待解决的主要问题有:构造滑移约束曲面、生成中间构型初始解和中间构型的平衡迭代.一步法是由Guo等[1]于1990年提出的采用全量理论并广泛应用于零件初始设计阶段的一种快速有限元模拟方法.大量的数值验证表明,该方法可以提供较好的应变度量,但是由于仅考虑变形终了状态而忽略了变形历史导致应力度量不准确.多步成形模拟方法的工作最初见于Majlessi等[2-3]的文章,其采用基于最小势能原理和比例构造中间构型的方法,用膜单元分析了简单轴对称零件的成形.随后Lee等[4]在已知几何中间变形状态的情况下,应用多步模拟方法对方盒和油底壳零件进行了分析并优化了初始板料形状.Kim等[5-6]提出根据接触节点构造滑移约束曲面和截面线映射构造初始解的方法分析了S-Rail零件的成形过程.Guo等[7]提出了通过求解空间曲面面积最小构造滑移约束曲面的拟一步法,来提高应力的度量精度.Huang等[8]提出了修改的截面线弧长法来获得中间构型的初始解.Li等[9]提出了一种直接标量算法以实现快速更新多步模拟法构型间的应力.Tang等[10]将拟一步法扩展到一般三维状态下,并提出一种针对中间构型间平衡迭代时的空间滑移策略.Halouani等[11]提出了自由曲面纠正的方法构造中间构型的初始解,并将拟一步法应用到轴对称冷轧成形分析中.
本文在一步法的基础上提出多步成形模拟方法来提高对最终零件的应力评估精度.
1 运动几何关系
考虑如图1所示的3个构型:初始平板、中间构型和最终零件间的非线性运动几何关系.以初始平板构型C0为参考构型的C1构型上的应变增量度量几何关系与一步逆成形法的参考平板构型的非线性几何关系是一致的.为引入变形后参考构型的弯曲效应,本文仅推导变形后参考中间构型C1的最终零件构型C上的应变增量度量.
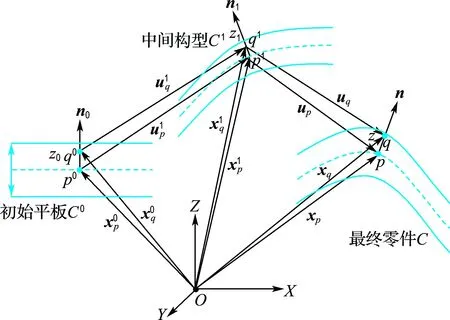
图1 运动关系示意图
考虑最终零件构型的中性层上的物质点p和沿其法向无限接近的点q:

(1)
式中:n和n1分别为物质点p和p1处的法向,dn1不为0反映了参考中间构型C1的弯曲程度.式(1)写为如下的矩阵形式:
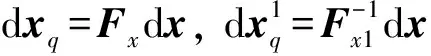
Fx=(o1+zn,xo2+zn,yn)=T(I+zb)
(z1n1,xz1n1,y0)
(2)

由此可以建立中间构型与最终构型间的变形梯度张量:
(3)
同样的,左柯西-格林变形张量的逆可以表示为
(4)
式中系数如下:
a=A0(1+zr)2+2B0sz(1+zr)+C0(sz)2;
b=A0(1+zr)sz+B0(1+zr)(1+zt)+
B0(sz)2+C0sz(1+zt);
c=A0(sz)2+2B0sz(1+zt)+C0(1+zt)2
(5)
和
A0=a0-z1n1,x(2(o1-up,x)+z1(n1,x));
B0=b0-z1((o2-up,y)n1,x+(o1-up,x)n1,y+
z1n1,xn1,y);
C0=c0-z1n1,y(2(o2-up,y)+z1(n1,y))
(6)
其中a0、b0和c0与一步逆成形法[1]中的系数一致.
从式(6)中可以看出,当z1=0,物质点位于中性面时,该应变增量度量退化为一步逆成形法的几何关系;当z1≠0,物质点位于厚度方向时,参考构型是已变形弯曲的中间构型C1,由于弯曲效应此有限应变增量度量不再等同于一步逆成形法的应变度量方式.
2 本构方程
本文采用厚向异性弹塑性耦合各向同性硬化(Power-Law硬化)材料模型,结合Hill48塑性势、关联流动法则和隐式返回算法更新应力与应变状态.总变形梯度张量F根据乘法分解为弹性Fe和塑性Fp部分,为满足客观性要求,应变与应力等度量均在共旋系下操作,考虑到金属成形中的小弹性应变假设,应变率可近似按加法

e+Dp分解为弹性部分Jaumann率

ε.
e和塑性部分Dp.
Hill48的二次塑性势函数定义为
(7)
式中:σ是柯西应力张量;P是各向异性矩阵;q是用于计算各向同性硬化的内变量,通常取为累积塑性应变.
根据关联流动法则,塑性应变率可表示为
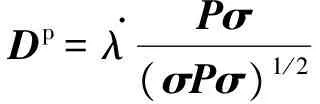
Dp=λ.Pσ(σPσ)1/2
(8)
式中:λ为拉格朗日塑性乘子,并通过一致性条件

f.
(σ,q)=0求得
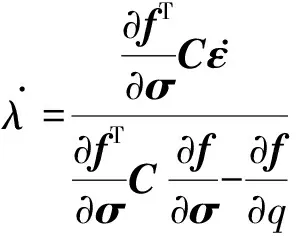
λ.=∂fT∂σCε.∂fT∂σC∂f∂σ-∂f∂q
(9)
利用上式可求得应力率为
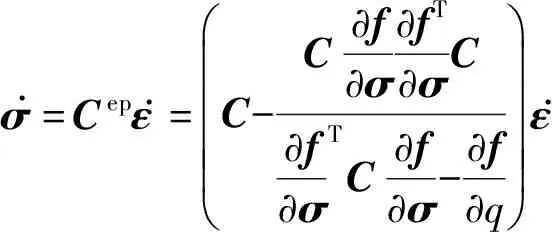
σ.=Cepε.=C-C∂f∂σ∂fT∂σC∂f∂σTC∂f∂σ-∂f∂qæèççççöø÷÷÷÷ε.
(10)
采用经典弹性预测塑性返回算法以更新应力状态.(n+1)时刻第i次迭代的更新应力可由下式计算:
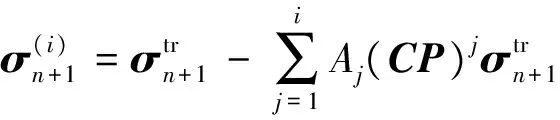
(11)
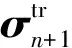
多步成形模拟方法采用较少的中间构型,使得构型间的有限应变增量取值较大,从而导致应力更新的图形返回算法迭代收敛困难.鉴于在一步法中广泛采用的弹性厚向异性假设,可以得到泊松比与厚向异性系数存在的关系:
ν=r/(1+r)
(12)

3 中间构型
3.1 滑移约束曲面
鉴于采用最小曲面作为目标函数的优化模型是极难以进行求解的,作者等提出了采用拟最小面积法以获得可以高效求解的优化模型[12].该方法假定滑移约束曲面是在凸模、凹模约束下的所有可能形状中面积平方最小的曲面,则目标函数修改为

(13)

经过代数运算,单元面积的平方可表示为
(14)
其中ξe是单元的基本变量向量,He和Ce类似于单元的刚度矩阵和内力向量.
同样的,按组装单元刚度矩阵和内力向量的方式整合该面积坐标矩阵和向量,则目标函数式(13)变为
(15)
其中ξ、H和C分别对应于结构的基本变量向量、面积矩阵和面积向量.原问题即转化为一个可在多项式时间内求解的二次规划问题.本文采用Matlab/quadprog( )进行求解.
此时,人为假定容许误差E,则任何满足条件
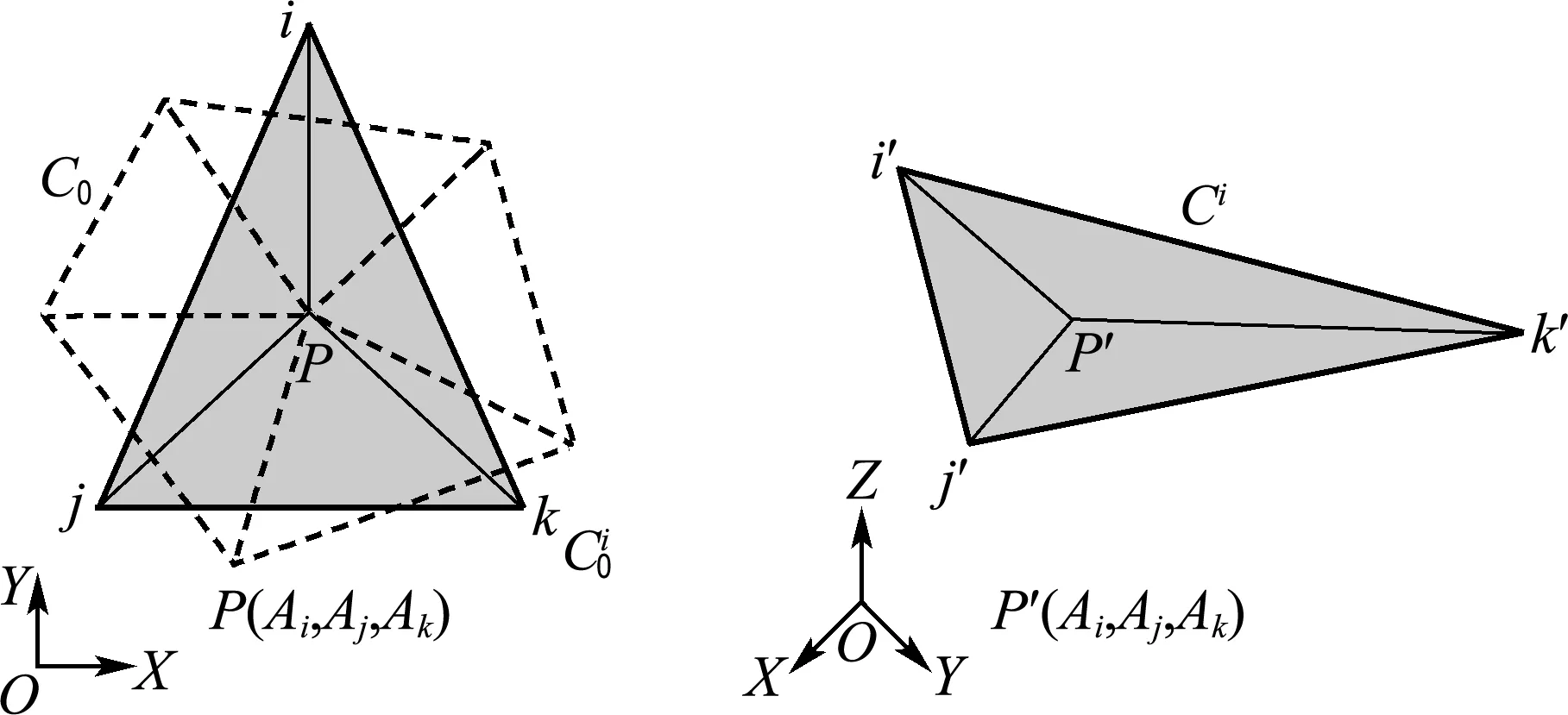
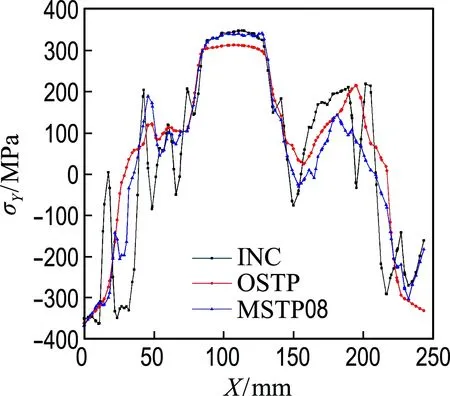
ξ (16) 的节点处于与凹模或凸模接触的状态.据此,可遍历节点筛选得到与工具网格接触的节点,基于这些接触节点采用直接连接接触边界或Delaunay三角网格的方法重新构造滑移曲面的侧壁部分,以改善拟最小面积法构造的侧壁,本文称为强化的PMA方法(EPMA方法). 由上一节构造的中间构型的滑移约束曲面仅为几何曲面,本节则采用直接映射物质点到滑移曲面上的方法生成初始的中间构型,即中间构型的初始解.其基本思想为构造的中间构型是成形过程中的临时状态,则其对应的初始坯料与最终已知零件的初始坯料是一致的.由此可以求得中间构型的初始解,其主要步骤为 (2)同样求解最终构型C得到初始平板构型C0; 图2 物质点映射示意图 (4)利用物质点的唯一标识,在滑移曲面构型Ci上的单元编号ep内,依据面积坐标P(Ai,Aj,Ak)创建点P变形后对应物质点P′; (5)循环投影所有物质点,则得到了位于滑移约束曲面上的中间构型的初始解. 该过程可进行多次直至前后两次初始解趋于一致,以避免过大的工艺补充面阻碍材料流动而影响一步法求解的坯料精度. 通过以上拟最小面积法和初始解构造方法,可快速生成若干真实的中间构型,然而注意到初始解构造过程中采用的一步法是基于全量理论的,因此要进行采用流动理论更新应力方法的中间构型间的平衡迭代. 考虑一阶线性三角形单元,其单元刚度矩阵和内力向量为 (17) 式中:he和Ae为单元的厚度与面积,B为局部系下的单元应变操作矩阵. 由于平衡迭代过程中,中间构型上的物质点被约束在滑移曲面上移动,通过罚函数的方法施加单元刚度矩阵约束: Ke=BTCepBheAe+γNTN (18) 式中:γ为经试错法确定的罚函数系数,N是单元的节点法向矩阵. 利用从全局系到局部系的单元坐标变换矩阵Q,得到全局系下的单元刚度矩阵和内力向量: (19) 经组装可得到结构的残余力向量: R(U(i))=Fext-Fint(U(i))=KΔU≠0 (20) 采用Newton-Raphson迭代求解: U(i+1)=Ui+ΔU (21) 某汽车弹簧盒支座的几何形状如图3所示,材料参数如下:弹性模量207 GPa,泊松比0.28,屈服应力154.31 MPa,幂指数硬化模量520.4 MPa,硬化参数0.232,平均各向异性系数1.653.成形工艺参数:压边力15 kN,摩擦因数0.15. 图3 弹簧盒支座零件的CAD模型 图4给出了拟最小面积法求解的中间构型在凸模行程15 mm和25 mm时的比例系数ξ的分布.其中灰色区域表示满足筛选条件式(16)(ξ<0.01或1-ξ<0.01),处于与凸凹模接触状态的单元. 为评估本文提出的中间构型构造方法的有效性,图5展示了由Ls-dyna增量法(INC)和多步成形模拟方法计算的各中间构型上截面线AB(见图6)的Z向坐标值比较. 可以看出针对15 mm构型时,PMA方法构造的中间构型在坐标范围-55~-40 mm(20~60 mm)内低于、在坐标范围-75~-55 mm(60~80 mm)处高于INC的中间构型.观察此中间构型的比例系数分布图4(a)发现,只有曲面A和D上的节点处于接触状态(灰色区域).结合接触节点集合和Delaunay三角网格法,重新构造的零件的侧壁与INC方法得到的中间构型相吻合,如图5中的EPMA曲线. 对于25 mm的中间构型,PMA方法的截面线仅在坐标范围-55~-40 mm(20~60 mm)内低于INC的,观察其构型的比例系数分布可以发现,曲面A、C和D均处于接触区域,而其他曲面处于非接触区域,通过EPMA方法重新生成的侧壁与INC的结果保持一致. 图4 中间构型比例系数ξ的分布 图5 中间构型上截面线AB的形状 (a) 15 mm (b) 25 mm 图6 中间构型的等效应力分布 Fig.6 Distributions of equivalent stress for middle configurations 针对凸模行程35 mm时的中间构型,PMA、INC和EPMA 3种方法的中间构型趋于一致,这是由于35 mm时,曲面A、B、C和D全部处于接触状态,构造的中间构型的曲面之间连接的侧壁部分趋同于凹模的侧壁形状,此时,该3种方法得到的中间构型是没有差别的. 由此可见,EPMA方法可有效改善PMA方法构造的中间构型的侧壁.图6给出了两个中间构型的等效应力分布. 为表明该多步成形模拟方法在考虑了若干中间构型对最终零件应力估计精度的改善,图7展示了由增量法、8个中间构型的多步法(MSTP08)和一步法(OSTP)计算的截面线CD(见图6)的X和Y方向上的应力分量分布图. 从图7中可以看出,整体趋势上多步法估计的应力分量分布曲线与增量法计算的应力分布保持同步的变化,而一步法不能提供经历复杂变形历史位置点的有效应力估计.在截面线X坐标约25 mm处,增量法估计的X应力分量存在明显的局部峰值(约250 MPa)和谷值(约-100 MPa),Y应力分量有最小值(约-350 MPa);而一步法估计该处的应力分量分布均变化较平缓,分别对应X应力分量的约-15 MPa和10 MPa及Y应力分量的-100 MPa;多步法预示了相应处的X应力分量局部峰值(约125 MPa)和谷值(约-75 MPa),及Y应力分量的最小值约-200 MPa.类似的对应力分量的改善在X坐标值约50 mm和200 mm等处观察到. 可以发现,采用多步法显著地改善了最终零件上的拉压应力状态的估计精度,如修正了X坐标25 mm处的X应力分量的局部峰值分布,提高了Y应力分量的应力精度. (a) X应力分量 (b)Y应力分量 图7 最终构型截面线CD上的应力分量 Fig.7 Stress components of section lineCDon final configuration (1)以拟最小面积法建立的二次规划模型来高效生成滑移约束曲面,并根据设定阈值筛选接触节点和Delaunay三角网格法以改善滑移约束曲面的侧壁使之符合真实变形情况.借助直接映射物质点的方法生成初始解构型,并采用施加罚函数约束的方式使构造的中间构型达到平衡状态. (2)重新推导了基于中间构型的有限应变增量度量,以考虑已发生变形的参考构型本身的弯曲效应对中性层外物质点的影响. (3)通过对盒支座零件的分析验证了强化的拟最小面积法生成的中间构型质量,表明了考虑8个中间构型的多步法预测的应力分布的精度,修正了一步法预估的最终零件上的错误的拉压应力和局部极值应力分量分布,并得到了与增量法的应力估计趋势相一致的结果. [1] GUO Y, BATOZ J, DETRAUX J,etal. Finite element procedures for strain estimations of sheet metal forming parts [J].InternationalJournalforNumericalMethodsinEngineering, 1990,30(8):1385-1401. [2] MAJLESSI S A, LEE D. Further development of sheet metal forming analysis method [J].JournalofEngineeringforIndustry, 1987,109(4):330-337. [3] MAJLESSI S A, LEE D. Development of multistage sheet metal forming analysis method [J].JournalofMaterialsShapingTechnology, 1988,6(1):41-54. [4] LEE C H, HUH H. Three dimensional multi-step inverse analysis for the optimum blank design in sheet metal forming processes [J].JournalofMaterialsProcessingTechnology, 1988,80-81:76-82. [5] KIM Seungho, KIM Seho, HUH H. Finite element inverse analysis for the design of intermediate dies in multi-stage deep-drawing processes with large aspect ratio [J].JournalofMaterialsProcessingTechnology, 2001,113(1/2/3):779-785. [6] KIM S H, HUH H. Construction of sliding constraint surfaces and initial guess shapes for intermediate steps in multi-step finite element inverse analysis [J].JournalofMaterialsProcessingTechnology, 2002,130-131:482-489. [7] GUO Y Q, LI Y M, BOGARD F,etal. An efficient pseudo-inverse approach for damage modeling in the sheet forming process [J].JournalofMaterialsProcessingTechnology, 2004,151(1/2/3):88-97. [8] HUANG Ying, CHEN Yiping, DU Ruxu. A new approach to solve key issues in multi-step inverse finite-element method in sheet metal stamping [J].InternationalJournalofMechanicalSciences, 2006,48(6):591-600. [9] LI Y M, ABBES B, GUO Y Q. Two efficient algorithms of plastic integration for sheet forming modeling [J].JournalofManufacturingScienceandEngineering-TransactionsoftheASME, 2007,129(4):698-704. [10] TANG Bingtao, LI Yunjiang, LU Xiaoyang. Developments of multistep inverse finite element method and its application in formability prediction of multistage sheet metal forming [J].JournalofManufacturingScienceandEngineering-TransactionsoftheASME, 2010,132(4):041013-041019. [11] HALOUANI A, LI Yuming, ABBES B,etal. Simulation of axi-symmetrical cold forging process by efficient pseudo inverse approach and direct algorithm of plasticity [J].FiniteElementsinAnalysisandDesign, 2012,61:85-96. [12] 刘伟杰,胡 平,周 平,等. 板材多步逆成形中的滑移约束曲面优化构造方法[J]. 机械工程学报, 2012,48(4):21-25. LIU Weijie, HU Ping, ZHOU Ping,etal. Research on intermediate configurations of multi-step inverse approach in sheet metal forming [J].JournalofMechanicalEngineering, 2012,48(4):21-25. (in Chinese)3.2 构造初始解

3.3 中间构型的平衡迭代
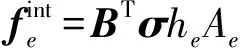
4 数值模拟






5 结 论
