基于离散量和用户兴趣贴近度的协同过滤推荐算法

,,,

(西北农林科技大学 信息工程学院,西安 710000)

0 概述

协同过滤推荐算法的关键步骤是计算用户或项目之间的相似度[1]。传统的相似度计算方法有余弦相似度、相关相似度以及修正的余弦相似度等[2-4]。传统相似度计算方法计算的相似度结果存在诸多问题,目前,研究者从多个方面对相似度计算进行了改进[5-7]。如文献[8]借用Sigmoid函数对相似度计算进行了改进,从一定程度上提高了准确率;文献[9]在文献[8]的基础上从用户评分相似度、兴趣的倾向相似度、置信度等方面对相似度计算方法进行了改进,提出了基于用户属性和评分的协同过滤算法(Collaborative Filtering Recommendation Algorithm Based on User Attributes and Scores,US-CF),但相似度计算结果仍存在很多问题。在评分数据丰富的情况下,传统相似度计算方法能够较为准确地计算出目标间的相似度[10]。然而在实际推荐过程中可用的评分数据稀少,使得系统难以搜寻到目标用户真正的邻居,产生了数据稀疏性问题[11-12]。部分学者采用数据填补技术降低评分数据的稀疏性,但存在信息失真或者填充值不可靠的问题[13-15]。另外在用户评分数据极端稀疏和用户间共同评分项较少的情况下,余弦相似度不能区分平行评分向量之间的相似度,相关相似度以及修正的余弦相似度出现无法衡量部分用户间兴趣相似程度的现象,导致推荐过程中得到的相似用户不准确,进而影响推荐系统的推荐质量[16-17]。

为了解决以上问题,本文提出一种基于离散量和用户兴趣贴近度的协同过滤算法(Collaborative Filtering Recommendation Algorithm Based Discrete Contents and User Interests Appropinquity Degree,DA-CF)。在该算法中,通过利用离散量相关的性质以及用户兴趣贴近度设计一种新的用户相似度计算方法。

1 传统相似度计算问题分析

传统的相似度计算方法有余弦相似度(Cosine,COS)、修正余弦相似度(Adjusted Cosine,ACOS)、Pearson相似度(Pearson Correlation Coefficient,PCC)等[5]。计算用户相似度是基于用户的协同过滤的关键步骤,其计算结果的好坏,直接影响推荐精度[18]。以上的传统相似度计算方法均存在缺点,以下的例子说明传统方法的缺陷。如表1是用户项目评分表,为计算方便,采用了9个用户对4个项目的评分值,其中用户用{u1,u2,…,u9}表示,项目用{i1,i2,i3,i4}表示,“—”表示未评分项目,在实例计算中用0替代。

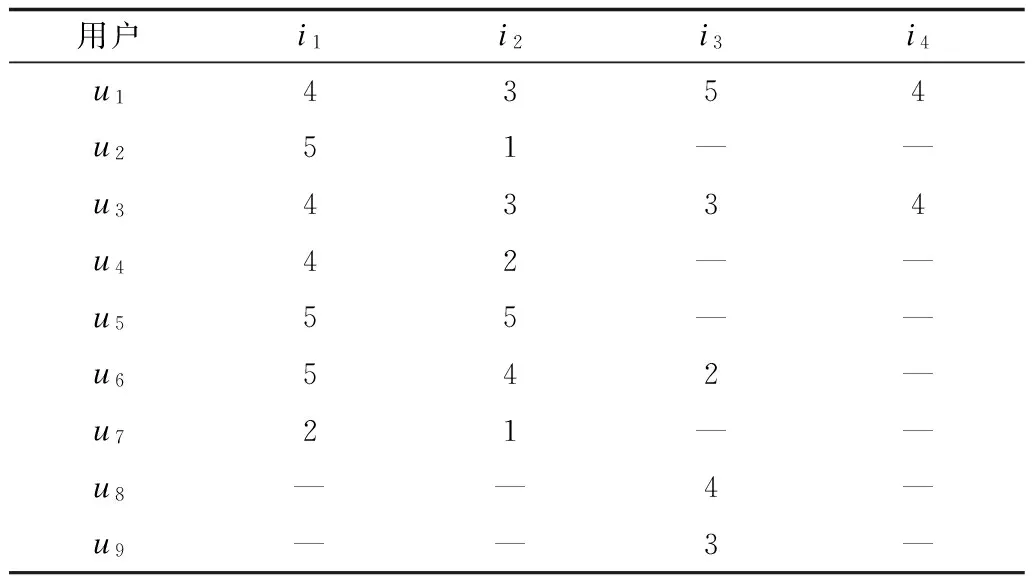
表1 用户项目评分

本文中利用矩阵S=(sij)n×n表示相似度计算结果,其中,n={1,2,…,9},sij表示用户ui和uj之间的相似度。以余弦相似度方法、修正余弦相似度方法、Pearson相似度方法、US-CF算法[9]为例,分析目前的相似度计算方法存在的问题,4种算法的相似度计算结果分别对应于矩阵SCOS、SACOS、SPCC和SUSCF。

分析以上计算结果,可知传统相似度计算存在以下问题:

1)相似度无法计算。由结果矩阵SPCC和SUSCF可知,PCC和US-CF方法计算相似度时,均出现了无法计算的现象(NaN),原因在于当公式分母计算结果为0时,此2种方法计算失效。在数据量极其稀疏时,此情况经常出现。

2)相似度失真。u1的评分向量为(4,3,5,4),u3为(4,3,3,4),两者均评价了较多的项目,并且有75%的项目评价分数完全一样,具有较大的相似度。而在结果矩阵SACOS和SPCC中得到的相似度为0,同时SUSCF中得到的相似度也较低。

3)相似度虚高。u4的评分向量为(4,2,0,0),u7为(2,1,0,0),虽然两者具有两项共同评分项,但u4评分值较高,对i1、i2有较大兴趣,而u7评分较低,对i1、i2有较低兴趣,在矩阵SCOS和SPCC中均得到相似度为1,在SACOS中得到的相似度同样很高。

4)相似度难以区分的现象。结果矩阵SCOS、SACOS、SPCC和SUSCF中均出现了部分相同或十分相近的数值,导致相似度无法区分。由3)中分析知,u4对i1、i2有较大兴趣,而u7对两者的兴趣较低,即u4和u7兴趣不同。而在SCOS中,u1和u4、u1和u7的相似度相同,均为0.606,若根据用户u1的兴趣为u4和u7进行推荐时,很可能会将用户兴趣较低的项目推荐给用户,从而导致推荐质量下降。

5)相似度计算忽略了共同评分项数以及相同评分值项数对兴趣的影响。用户评分项目越多,共同评分项越多,并且具有相同评分项数越多,可以认为具有较高的相似度[13]。基于此,u1和u3的相似度应该最高,但矩阵SUSCF中u2和u4的相似度高于u1和u3的相似度,而SPCC中u2和u4以及SCOS中u4和u7的相似度均高达1。

6)相似度计算忽略评分偏好对兴趣度的影响。u5的评分向量为(5,5,0,0),u7为(2,1,0,0),u5对项目1和2的倾向度明显大于u7,但矩阵SCOS和SACOS均得到较大的结果,分别为0.949和0.948。SPCC中对此情况计算无效,SUSCF中反而呈现出极低的相似度0.033。

以上问题导致了计算相似度时准确度不高,最终导致传统推荐算法的推荐结果不理想,若要解决相似度计算出现的种种问题,则需更深入地挖掘用户评分中所隐藏的兴趣信息,本文提出一种新的相似度计算方法,用于改进传统协同过滤算法。

2 改进的协同过滤算法原理

离散量考虑的是全部个体的总信息量,在离散量的基础上建立信息相似系数测度,可以得到更为全面的相似度信息,但是往往会忽略个体间的差异信息,贴近度更偏重于信息组成颗粒间的差异程度,体现了个体间的差异性,能够弥补离散量构建信息相似系数测度的不足。本节从全信息量的角度深入挖掘评分与用户兴趣间的关系,揭示用户评分之间的相似度,利用离散量相关理论来对相似度计算进行改进,同时利用用户兴趣贴近度对相似度进行加权处理,最终得到较为准确合理的相似度计算结果。

2.1 基于离散量的相似度计算方法

Shannon把“熵”从物理学领域引入到信息学领域,将信息中排除冗余后的平均信息量称为“信息熵”,并利用概率论与逻辑方法推导出信息熵的计算公式[19-21]。用X表示信源,该信源发出的信号用xi表示,相应地发出各信号的先验概率为p(xi),其中i=1,2,…,n,则对该信源的信息熵H(X)定义为式(1),其中使用以2为底的对数函数,熵的量纲为比特。

(1)

与Shannon信息量相平行,本文中将引入离散量(Discrete Contents,DC)及其基本性质。对于状态空间X={x1,x2,…,xr},在总和N=n1+n2+…+nr的条件下,xi分别出现ni次,其中i=1,2,…,r,则认为状态空间构成一个离散源[22-24],表示为式(2)。

(2)

从信息论的角度上,度量离散性的量称为离散量,记为D(n1,n2,…,nr)。

定义1对于离散源(式(2)),离散量定义[23-24]:

(3)

根据式(3),可以引申出式(4)和式(5)。

(4)

(5)

由式(4)可以看出,D(X)和N有关系,刻画了N约束下ni的离散性。而式(5)表示了离散量和信息熵之间的关系,用H(X)和D(X)分析同一事物,没有绝对的相关性。根据信息熵的定义可以看出,H(X)表示信源X中每个个体所携带的平均信息量,而式(5)可以看出,离散量D(X)表示信源X中全部个体的全信息量。由式(5)可知,离散量同样具有信息熵的性质,即具有非负性、可加性、等倍增性以及和的离散量不小于各离散量之和等性质[24]。

在本文的推荐系统中,假设用户U和用户V对项目集合的评分矩阵分别为矩阵U和V:

(6)

(7)

评分矩阵公式式(6)和式(7)从空间角度可以理解为评分向量,从信息论角度可以理解为离散评分源。根据离散量的性质——和的离散量不小于各离散量之和,可以得到评分数据的离散增量:

Δ(U,V)=D(U+V)-D(U)-D(V)

(8)

评分数据的离散增量同样具有非负性和对称性,是一种半角度的距离测度或者称为广义距离测度,它从信息量的角度刻画了2个离散评分源之间的相似度,称为信息系数测度[24]。信息系数测度越小,表示2个离散评分源之间越相似,否则越相异。根据离散量可加性以及等倍增性,还可以将评分数据的离散增量表示为:

(9)

当评分数据ni或mi之一等于0时,D(ni,mi)=0,由此可得:

0≤Δ(U,V)≤D(M,N)

(10)

由式(9)和式(10)联合可以得到如下关系:

(11)

(12)

由式(11)可以得到评分数据的相似信息系数,用于度量2个用户之间的相似程度,本文使用的相似度计算方法表示为式(12),I1即为基于离散量的相似度计算方法,利用该式计算出来的相似度结果如矩阵SI:

SI=

由结果矩阵SI可以看出,基于离散量的相似度计算方法充分挖掘评分项之间的关系,得到了初步的相似度计算结果,但由于式(12)只考虑了评分项目之间的关系,忽略了用户之间的兴趣倾向与共同偏好,在一定程度上放大了用户间的相似程度,为此,将使用用户兴趣贴近度进行修正。

2.2 用户兴趣贴近度的修正方法

2.1节从全信息量的角度刻画了用户评分信息间的贴近程度,给出了基于离散量的相似度度量方法(式(12)),该方法深入地挖掘和分析了用户评分间的信息关系,但以上方法未关注用户兴趣偏好问题。用户评分项目越多,共同评分项越多,并且具有相同评分项数越多,可认为具有较高的相似度[13]。基于此假设,本节提出用户兴趣贴近度的概念,见定义2。

定义2设项目集合I={i1,i2,…,in},u和v是I上的评分集合,则称:

(13)

为u与v的用户兴趣贴近度。其中,α称为可信度因子,见式(14),可信度因子用来表示用户之间共同评分项目与所有评分项目的关系,表示用户之间实际兴趣贴近关系。其中,Cu,v表示用户u和v的共同评分项目集合,|Cu,v|表示共同评分项目数,ru,i表示用户u对项目i的评分,Iu表示用户u的评分集合,评分范围为整数1～5。

(14)

由式(14)可知,0≤α≤1。当用户u与用户v没有共同评分项时,α=0。当用户u与用户v的共同评分项集合与两者的所有评分项集合完全一致时,α=1。

当α=1时,可信度因子调节失效,针对此特殊情况,用户兴趣贴近度参考海明贴近度[23]的形式,将其改进为评分环境下的海明贴近度公式,如式(15)的形式,其中,Iu,v表示用户u和v共同评分项目集合。

(15)

2.3 融合离散量和兴趣贴近度的相似度计算方法

经过2.1节和2.2节的分析,本节得到融合离散量和用户兴趣贴近度的相似度计算方法。在计算过程中分用户间的可信度因子α≠1和α=1,本文所提出的相似度计算方法如下:

(16)

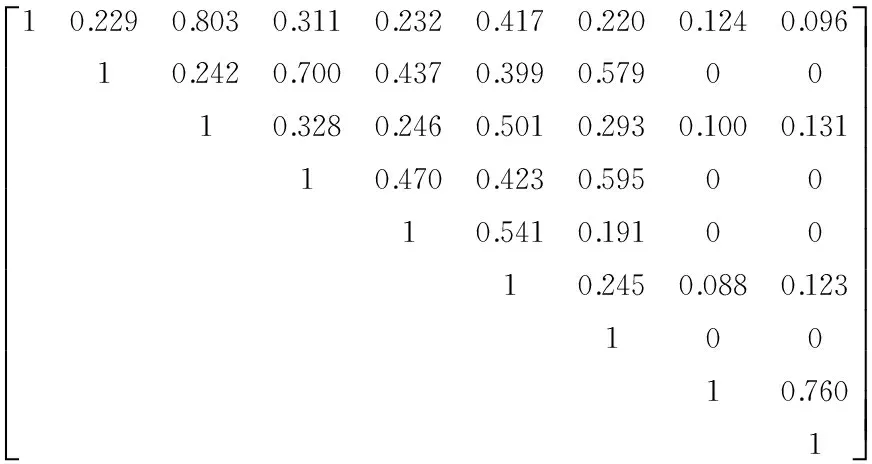
最终,经过式(13)和式(15)修正后的相似度计算结果如矩阵SSIM所示,其中0值表示相似度为0,例如u2和u8、u2和u9都没有公共项,因此相似度为0,属正常计算结果。从结果矩阵中可以看出,本文算法计算的相似度计算结果能准确合理地体现用户间的相似度,解决了以上提到的6个问题以及其他潜在问题,提高了用户之间相似度的区分性,从而为推荐系统解决了核心的相似度计算问题,有利于后续的评分预测和个性化推荐。

SSIM=

2.4 协同过滤算法

根据2.3节提出的融合离散量和用户兴趣贴近度的相似度计算方法,本节利用新的相似度计算方法对协同过滤算法进行改造,则新算法的伪代码见算法1。

算法1基于离散量和用户兴趣贴近度的协同过滤算法

输入评分矩阵R,目标用户u和近邻数K

输出目标用户u对项目i的评分预测值Predu,i

2) for 所有用户 u in 测试集 Trm,ndo

3) D(u),D(v) ← 计算用户u和v的离散量,根据式(4)

4) D(u+v) ← 计算用户u和v联合的离散量,根据式(8)

5) D(u,v) ← 计算用户u和v评分和的离散量,根据式(4)和式(9)

6) I1← 1-[{D(u+v)-D(u)-D(v)}/D(u,v)] %计算信息相似系数测度

二级运算放大电路主要用于将一级放大结果放大调理以满足A/D转换芯片输入范围，获取最大的检测精度。其电路结构如图4所示。

7) if α≠1 then

8) σu,v(u,v) ← 计算用户兴趣贴近度,根据式(13)

9) end if

10) if α=1 then

11) σ’u,v(u,v) ← 计算用户兴趣贴近度,根据式(15)

12) end if

13) sim’’(u,v) ← I1·σu,v(u,v) or I1·σ’u,v(u,v) %计算最终的相似度结果

14) K ← u’∈N(u) %寻找活动用户u的K近邻

15) Predu,i← 计算目标用户u对未评分项目i评分预测值

16) end for

17) 计算测试集中预测评分的平均绝对误差

3 实验结果与分析

3.1 实验数据

实验数据为MovieLens,是由明尼苏达大学GroupLens小组提供的电影评分[16]。该电影数据集具有100k、1m、10m、20m等几个不同规模的评分集合,如表2所示,该数据集可以从网站www.grouplens.org下载所得。为说明验证本文的研究问题,采用ml-1m数据集,该数据集是在2000年,大约6 040名用户对接近3 900部电影的1 000 209个匿名评分数据,数据稀疏等级[17]为{1-[1 000 209/(6 040×3 900)]}=0.957 5,评分范围为整数1～5。数据集包含三方面内容,用户信息、电影信息、评分信息。用户信息包括用户ID、性别、年龄、职业以及邮政编码;电影信息包括电影ID、标题以及类别;评分信息包括用户ID、电影ID、评分值以及时间戳。

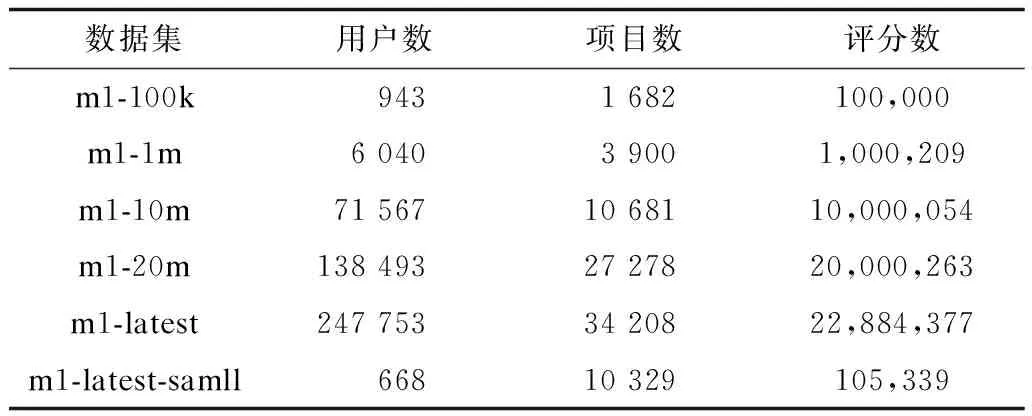
表2 MovieLens数据集规模

3.2 实验环境和度量标准

实验环境为安装Windows 10操作系统的PC机,内存16 GB,磁盘1 TB,处理器为英特尔Core i7-6700HQ。程序开发环境为Anaconda2 Spyder,Phython版本号为2.7版。

推荐系统有多种评估指标,如评分预测准确度、覆盖率、置信度、信任度等,评分预测准确度是目前推荐系统研究中讨论最多的指标,评分预测准确度的评价标准主要有均方根误差(Root Mean Square Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)、归一化均方根误差(Normalized Root Mean Square Error,NRMSE)和归一化平均绝对误差(Normalized Mean Absolute Error,NMAE)等。其中,MAE的应用最为广泛,本文实验结果选用MAE来评价。MAE可用来衡量预测的评价值同真实用户评价值之间的接近度,MAE值越小,预测效果越好。假设用户预测评分集合表示为P={pi|i=1,2,…,n},对应的用户实际评分集合为Q={qi|i=1,2,…,n}[25-26]。其中,n为物品个数,则MAE计算方法如下:

(17)

3.3 实验结果分析

首先对各种不同的相似度计算方法计算出的平均绝对误差(MAE)进行对比,分析本文所提出的相似度计算方法的效果;然后在相同数据集上进行对比实验,比较本文提出的新算法与传统算法的推荐质量,并对实验结果进行分析说明;最后在不同稀疏度的数据集上,验证本文算法在极度稀疏的数据集上的推荐效果。

3.3.1 最优用户邻居数

本次实验过程采用十折交叉验证方法(10-fold cross validation)用来测试算法的准确性。具体操作方法是将数据集分成10份,轮流将其中9份作为训练集,剩下的1份作为测试集,进行多次试验后,最终取均值。此方法的优势在于防止数据集之间的数据分布不均,同时多次验证取均值能有效降低因随机取样产生的误差。

本次实验的目的是寻找最优邻居数K,每次实验将K值从5增加到100,10次实验的MAE求均值,结果如图1所示。从图中可以清晰看到,本文提出的算法,在用户邻居数达到40附近时,计算出来的MAE值最小,因此最优用户邻居数选择为40。

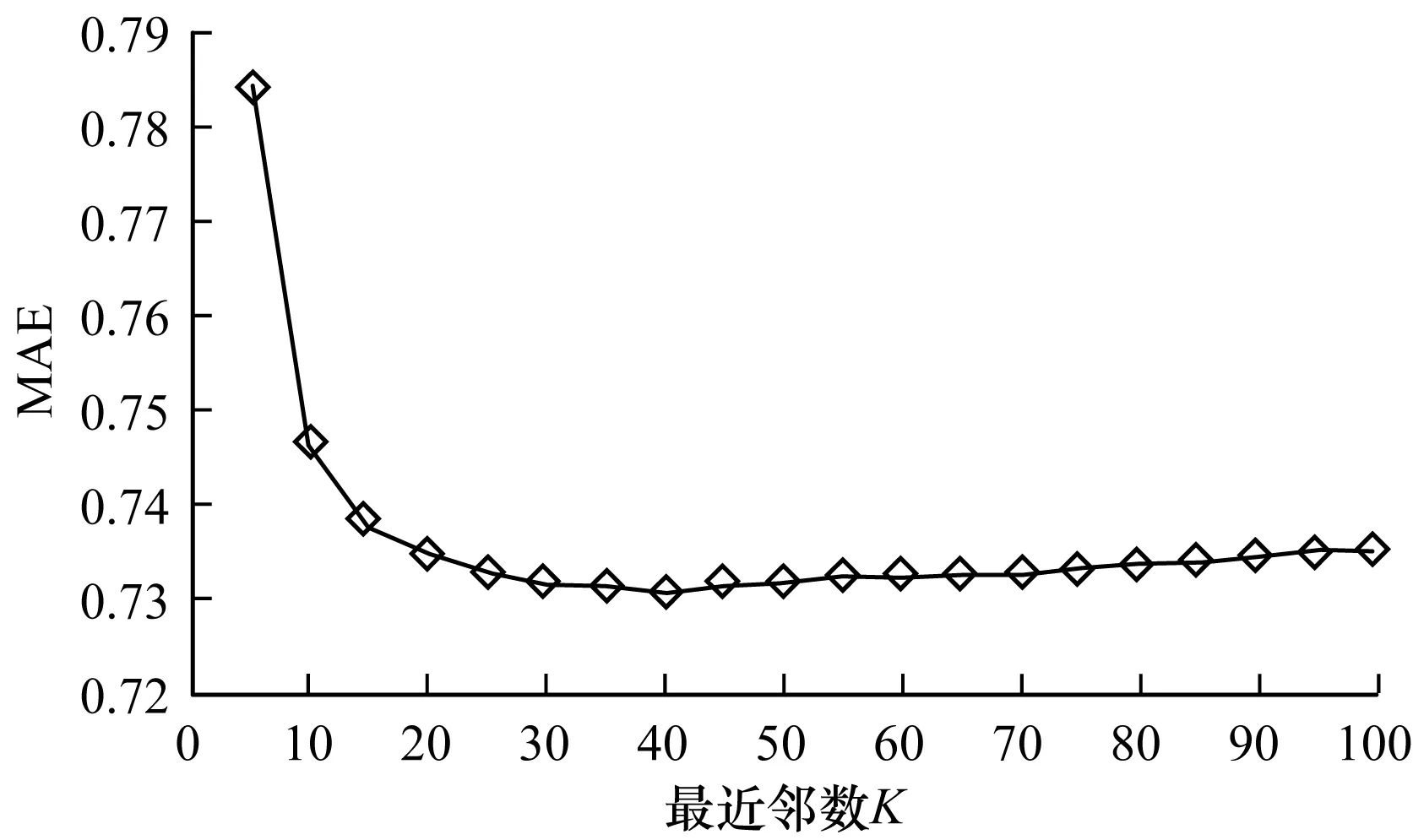
图1 MAE值随最近邻数K的变化情况

3.3.2 不同推荐算法的推荐质量比较分析

本次实验比较不同推荐算法的推荐质量,利用不同K值下的平均绝对误差(MAE)进行衡量,平均绝对误差值越小,推荐质量越好。

实验中,传统协同过滤算法采用不同的相似度度量标准进行近邻计算。所使用的算法有基于余弦的协同过滤算法(COS-CF)、基于修正余弦的协同过滤算法(ACOS-CF)、基于Pearson的协同过滤算法(Pearson-CF)、文献[9]中的算法(US-CF)以及本文提出的算法(DA-CF),实验结果如图2所示。

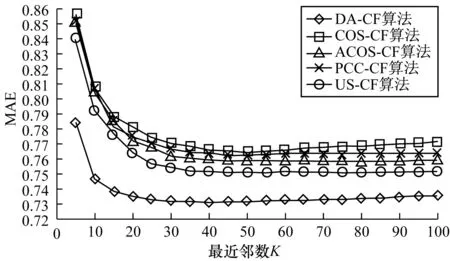
图2 不同相似度计算方法推荐质量比较

图2展示了各种算法在不同K值下MAE值之间的数量关系,整体而言,本文改进算法的MAE值明显低于传统算法。当最近邻居数K小于30时,各种算法MAE值都较高,随着最近邻居数的增加,各种算法的MAE值均急剧下降,本文改进的算法相较其他算法在最近邻居数为5时的MAE值最小,从最近邻数从5～30的增加过程中变化幅度比其他算法小;当K值大于30后,各种算法逐渐趋于稳定,本文算法的MAE值明显比其他算法更低,说明本文提出的算法在推荐精度方面优于其他算法,可以显著地提高推荐系统的推荐质量。

3.3.3 数据稀疏度对算法的影响

本次实验为比较在不同数据稀疏等级下,本文提出的算法(DA-CF)与3.3.2节中其他传统算法性能表现。将数据集中的评分数据随机进行删除调整,以实现数据稀疏度的变化,根据文献[17]的数据稀疏等级计算方法,将调整后的数据集稀疏度结果展示如表3所示。

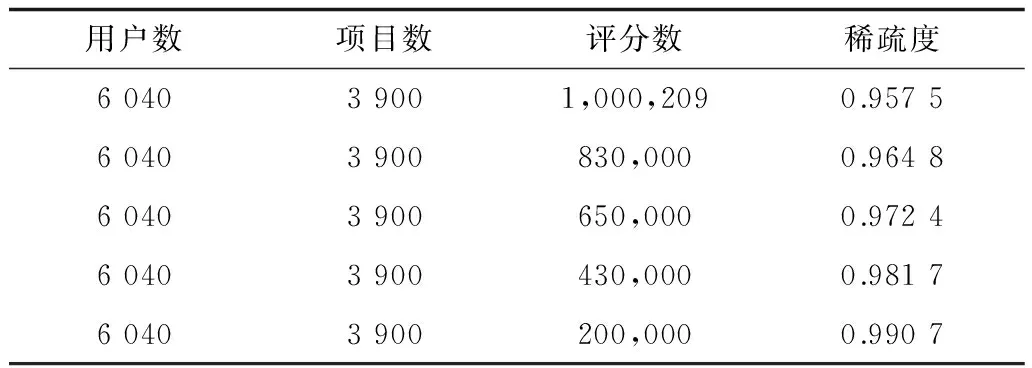
表3 数据集各种不同的稀疏度

本文实验结果如图3所示,从图中可以看出,随着数据稀疏度的变大,所有算法的性能均变低,但变化程度不一样,本文提出的算法(DA-CF)相对于其他算法而言,变化幅度最小,同时在各种场景下,MAE值最低,能较好地适应各种不同稀疏度的数据。由于DA-CF算法从全信息量的角度深入寻找评分与用户兴趣间的关系,因此在数据极度稀疏的情况下,也有较好的性能。

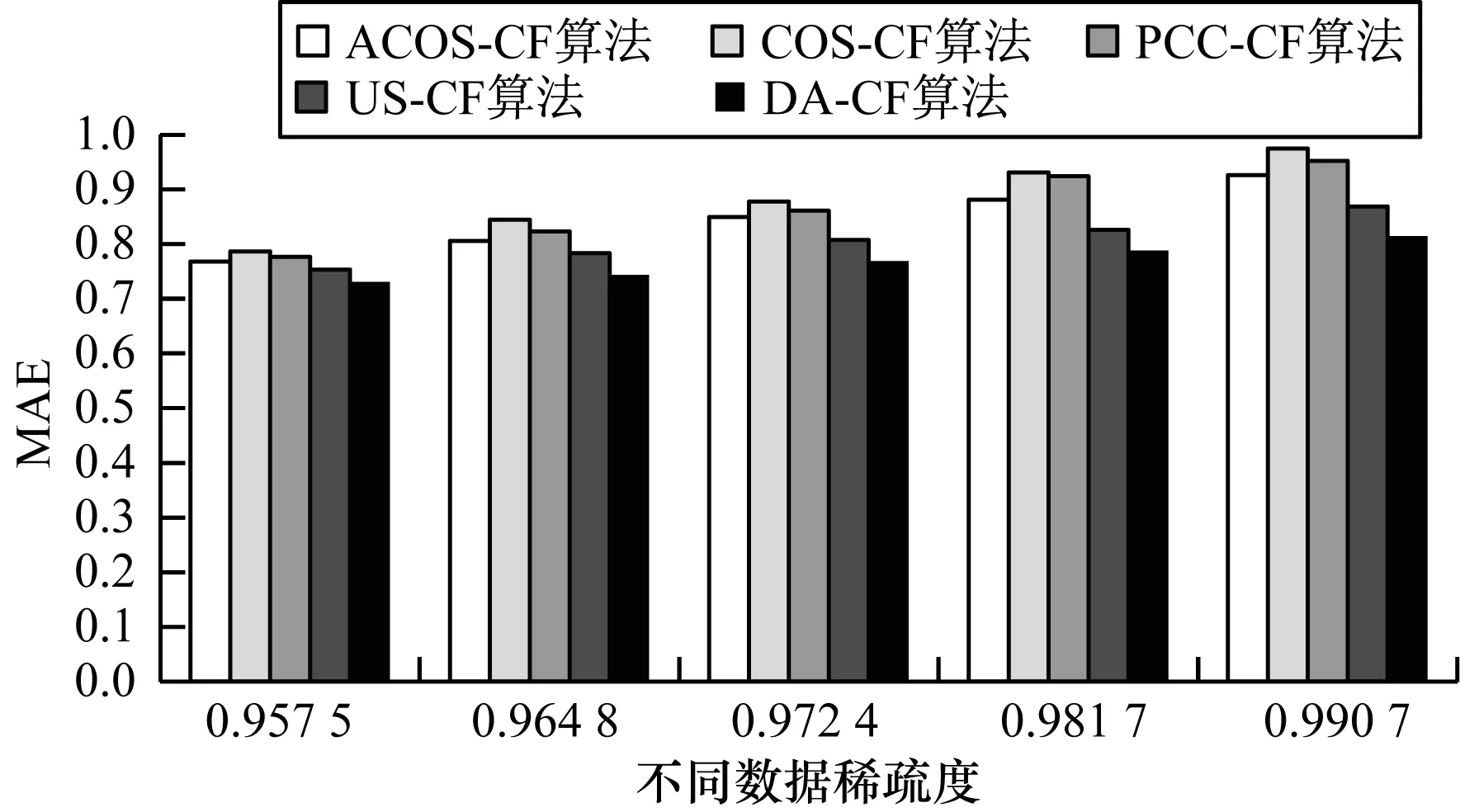
图3 数据稀疏度对不同算法性能的影响

4 结束语

本文提出基于离散量和用户兴趣贴近度的协同过滤算法。从用户评分全信息量和用户兴趣偏好2个方面,融合离散量和用户兴趣贴近度,进行用户相似度计算。实验结果表明,DA-CF算法较好地解决了常规相似度算法中存在的相似度无法计算、失真、虚高等现象,提高了系统的推荐质量,尤其在数据极端情况下,也能保持相对较好的推荐性能。在未来的研究中,可以结合更多的情境因素,缓解算法的冷启动问题,进一步提高算法的推荐质量。

[1] 文俊浩,袁培雷,曾 骏,等.基于标签主题的协同过滤推荐算法研究[J].计算机工程,2017,43(1):247-252.

[2] 孟祥武,刘树栋,张玉洁,等.社会化推荐系统研究[J].软件学报,2015,26(6):1356-1372.

[3] RICCI F,ROKACH L,SHAPIRA B,et al.Recommender Systems Handbook[M].Berlin,Germany:Springer,2011.

[4] 郭 迟,刘经南,方 媛,等.位置大数据的价值提取与协同挖掘方法[J].软件学报,2014,25(4):713-730.

[5] CHOI K,SUH Y.A New Similarity Function for Selecting Neighbors for Each Target Item in Collaborative Filtering[J].Knowledge-based Systems,2013,37(1):146-153.

[6] AHN H J.A New Similarity Measure for Collaborative Filtering to Alleviate the New User Cold-starting Problem[J].Information Sciences,2008,178(1):37-51.

[7] 时念云,葛晓伟,马 力.基于用户人口统计特征与信任机制的协同推荐[J].计算机工程,2016,42(6):180-184.

[8] LIU H,HU Z,MIAN A,et al.A New User Similarity Model to Improve the Accuracy of Collaborative Filtering[J].Knowledge-based Systems,2014,56(3):156-166.

[9] 丁少衡,姬东鸿,王路路.基于用户属性和评分的协同过滤推荐算法[J].计算机工程与设计,2015(2):487-491.

[10] 刘树栋,孟祥武.基于位置的社会化网络推荐系统[J].计算机学报,2015,38(2):322-336.

[11] 林耀进,张 佳,林梦雷,等.一种基于模糊信息熵的协同过滤推荐方法[J].山东大学学报(工学版),2016,46(5):13-20.

[12] 韩亚楠,曹 菡,刘亮亮.基于评分矩阵填充与用户兴趣的协同过滤推荐算法[J].计算机工程,2016,42(1):36-40.

[13] TSAI C F,HUNG C.Cluster Ensembles in Collaborative Filtering Recommendation[J].Applied Soft Computing,2012,12(4):1417-1425.

[14] 张燕平,张 顺,钱付兰,等.基于用户声誉的鲁棒协同推荐算法[J].自动化学报,2015,41(5):1004-1012.

[15] HUETE J F,FERNNDEZ-LUNA J M,CAMPOS L M D,et al.Using Past-prediction Accuracy in Recommender Systems[J].Information Sciences,2012,199(15):78-92.

[16] 钟 川,陈 军.基于精确欧式局部敏感哈希的改进协同过滤推荐算法[J].计算机工程,2017,43(2):74-78.

[17] 邓爱林,朱扬勇,施伯乐.基于项目评分预测的协同过滤推荐算法[J].软件学报,2003,14(9):1621-1628.

[18] 周泓宇,梁 刚,冯 程,等.结合正反相似度的协同过滤推荐算法[J].计算机工程,2016,42(10):51-56.

[19] WANG W,ZHANG G,LU J.Collaborative Filtering with Entropy-driven User Similarity in Recommender Systems[J].International Journal of Intelligent Systems,2015,30(8):854-870.

[20] 李卫东.应用多元统计分析[M].北京:北京大学出版社,2015.

[21] 汪 涛,王永智.基于信息熵的安徽省创意产业结构均衡度分析[J].新余学院学报,2017,22(1):43-47.

[22] 王保山,邵明星,丁爱亮,等.证券市场信息熵技术指标构建与应用[J].宁波大学学报(理工版),2012,25(3):79-82.

[23] 袁志发,宋世德.多元统计分析[M].2版.北京:科学出版社,2009.

[24] 丁世飞,靳奉祥,赵相伟.现代数据分析与信息模式识别[M].北京:科学出版社,2013.

[25] 李晓艳,张子刚,张逸石.集成K-means聚类和有监督特征选择的混合式协同过滤推荐[J].管理学报,2013,10(9):1362-1367.

[26] 刘旭东,吴旭军,陈德人,等.基于用户特征分解的协同过滤冷启动解决方法[J].山东农业大学学报(自然科学版),2013,44(4):616-619.