机床主轴径向回转误差的测量与研究
2018-01-19杨赫然郭学庆孙兴伟
杨赫然,郭学庆,孙兴伟
(沈阳工业大学 机械工程学院,辽宁 沈阳 110870)
0 前言
一台数控机床加工精度,由主轴部件的精度决定,因此主轴部件是保证机床加工精度的核心[1]。在精密机床加工工件的过程中,机床主轴的各种误差会降低加工工件的精度,而机床主轴的回转误差是影响机床工作精度的一个主要因素,会对加工工件的圆度误差、表面粗糙度产生直接的影响[2]。
理想状态下,主轴的回转轴线相对于某个固定参考系(例如工作台面)是固定不动的。但在实际的机床轴系中,由于轴承的内外圈圆度误差以及主轴上齿轮和其它传动件的制造和安装误差,使主轴在空间位置上的瞬时实际回转轴线总是不定的,把这些瞬时回转轴线的平均位置定义为主轴理想回转轴线[3]。主轴的实际回转中心线相对于理想回转中心线的空间位置的偏离尺度,定义为主轴回转误差。主轴回转误差是由回转误差运动引起的,包括主轴绕Z轴的自转运动,以及另外五个自由度的误差运动,分别为沿Z轴的轴向误差运动,沿X、Y轴的径向误差运动和绕X、Y轴的角度误差摆动,这些误差运动统称为主轴回转误差运动。其中径向运动和角度摆动总称为主轴径向回转误差,是影响加工误差的主要原因。主轴回转误差运动如图1所示。
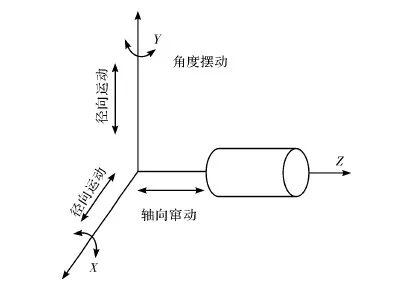
图1 主轴空间运动
在主轴的轴端面安装一个传感器,将采集到的信号数字化处理即可得到轴向误差。主轴轴向误差的测量方法比较单一,然而主轴径向回转误差的研究有多种方法,例如:多步法、自校正法、多探头法(也叫多点法)以及数理统计法等[4]。本文采用多探头线位移三点法对主轴回转误差进行分离。
1 误差分离与评定
1.1 误差分离原理
误差分离技术就是根据被测工件轮廓不变这一特性,将所测得的传感器输出信号通过数学分析和物理变换,把含有影响测量精度的信号分量给分离出去,从而得到所要测量的准确信号[5],最终实现工件的形状误差和回转误差的分离,过程如图2所示。将所测得的信号经过A/D转换,即模拟信号转换为数字信号,最后运用测量系统里的算法对数字信号进行处理,去除影响测量精度的信号分量,最后实现误差分离[6]。

图2 误差分离过程
1.2 回转误差分离方法
在实际的误差测量过程中,由于主轴回转轴心不可见,只能借助于安装在主轴上的标准球来间接测得主轴回转轴心运动,这样就会把标准球或主轴的圆度误差混入到测量数据中,因此要从采集到的数据中分离出回转误差,就需要采用一种正确地误差分离方法。
多探头线位移三点法误差分离技术是在回转轴的某一截面的周向位置,以不同的角度间隔,安装三个电涡流位移传感器,对主轴的回转运动进行测量[7]。不考虑其它影响因素,传感器采集的数据含有主轴的回转运动误差和形状误差,采用多探头法的矩阵算法误差分离技术对主轴回转误差和形状误差进行分离[8]。多探头法测量原理如图3所示。
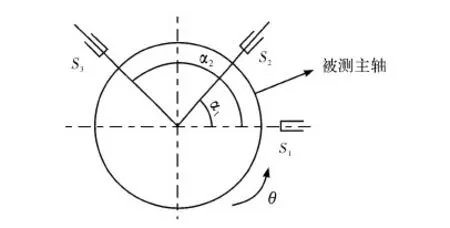
图3 多探头法测量原理
三个传感器的测量方程如下:
(1)
式中,yi(θ)为传感器读数,i=0、1、2;αi为各传感器安装位置与x轴的夹角,i=0、1、2;r(θ)被测试件圆度误差;dx(θ)、dy(θ)为主轴回转误差在x和y轴方向上的分量。
取α0=0,将θ离散化并以矩阵形式表示为
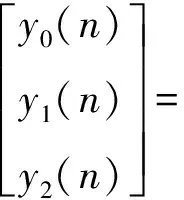
(2)
式中,n为采样点位置,n=0、1、2…N-1;N为传感器采样一周的点数;pi为传感器角位置编号,其中pi=Nαi/2πi=0、1、2。
把式(2)简化为Y=ER+AΔ;Δ代表主轴x和y回转误差,为了分离运动误差,左乘C,得到CY=CER+CAΔ;C=[c0c1c2],c0,c1,c2分别为传感器0、1、2所在通道的灵敏度。令CA=0则使系统参数满足
(3)
取c0=1,解方程组
(4)
式中,Δθ为采样点等分角度,Δθ=2π/N。
由yi(n)=CY,则
yi(n)=c0r(n)+c1r1(n+p1)+c2r2(n+p2)+(c0+c1cosα1+c2cosα2)dx(n)+(c1sinα1+c2sinα2)dy(n)
(5)
将c0、c1、c2代入式(1~5)化简后得
yi(n)=r(n)+c1r(n+p1)+c2r(n+p2)
(6)
式中,r(n+p0)、r(n+p1)、r(n+p2)分别为α0、α1、α2时延后的圆度误差离散形式。
在实际的实验测量过程中yi(n)是3个位移传感器输出信号(离散序列)的和。圆度误差r(n)也是个离散序列,且具有周期性r(N+n)=r(n),因此圆度误差也可以用一个离散序列来表示。
即
r(n)=[r0,r1,…,rp0,rp0+1,rp1,rp1+1,…,
rp2,rp2+1,…,rN-2,rN-1]T
(7)
经过时延后圆度误差r(n)的离散序列可以表示为
(8)
将式(8)与式(6)联立,并根据矩阵两边相等可得
yi(n)N×1=SN×Nr(n)N×1
(9)
式中,SN×N为三点法误差分离的系数矩阵。
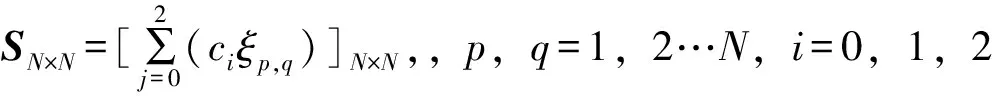
由于rank(SN×N,yi(n)N×1)=rank(SN×N)=N,因此根据线性方程组秩与解的关系可得,方程组有唯一解,可得圆度误差
(10)
根据圆度误差具有的周期性,可以求得r(n+p1)、r(n+p2)。
将分离出来的圆度误差r(n)代入式(1)可得径向运动误差如式(11)。
(11)
至此,通过式(10)和(11)就可以得到完全分离出的主轴圆度误差和回转误差。
1.3 圆度误差的最小二乘法评定
高精度回转体零件质量的高低一般用圆度误差来评价,鉴于最小二乘法计算简便,能够满足实际运行下的计算机处理速度,从而得到准确结果,因此本文采用该方法对主轴圆度误差进行评定。被测轮廓上的各点到某一定圆的距离的平方和为最小,此圆则为最小二乘圆。最小二乘法就是用来寻找理想圆(也称最小二乘圆),定义它的圆心为理想圆心。实际轮廓上的点与理想圆心之间的峰谷距离即为圆度误差。评定方法如图4所示。
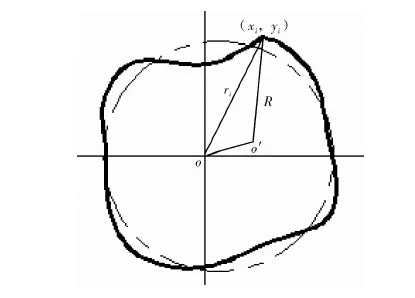
图4 圆度误差评定
利用该方法可以求出理想圆圆心坐标xi(a,b),半径为R。
(12)
式中,xi,yi为实际轮廓上各采样点;ri为采样点到坐标原点的距离。
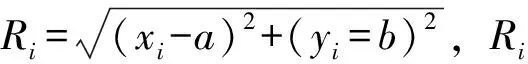
1.4 回转误差的圆图像评定
主轴回转误差评定就是定量求解回转运动误差的大小。评定主轴回转精度的方法有很多,本文采用圆图像的圆度误差值作为主轴回转精度的评价方式。
该方法首先形成一个以主轴回转角为自变量的基圆,然后将位移传感器输出的数据中分离出的主轴回转误差运动数据叠加到基圆上生成一个圆图像,以包容这个圆图像的两个同心圆的半径差即为主轴回转精度[9]。由于这种方法得到的理想圆的圆心唯一,且有完整的计算公式,因此优先选用此法。
2 测试系统设计
2.1 硬件系统构成
机床主轴回转误差测试系统主要由标准球、传感器、采集卡、计算机以及误差分离上位机组成,如图5所示。
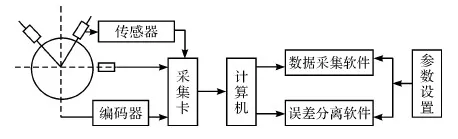
图5 硬件系统组成
2.2 软件设计
采用便于分离主轴回转误差的线位移多探头法的前提下,设计一套动态测试的模块化系统,该系统主要是实现测量原始数据的输入、对测量数据的处理和误差分离结果的显示,如图6所示。
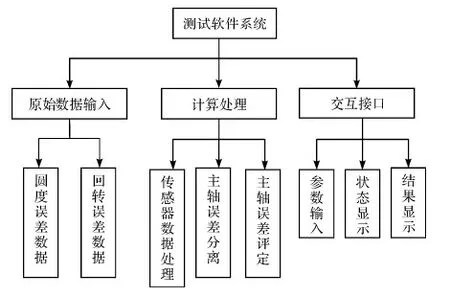
图6 软件系统流程
(1)原始数据输入包括3个电涡流位移传感器测得的主轴回转误差数据和形状误差数据。
(2)传感器数据处理是用安装在不同位置的3个传感器的位移变化序列来表示传感器读的数据序列。采用优化算法的矩阵算法对传感器测得的位移变化进行误差分离,然后分别用圆图像法和最小二乘法对主轴回转误差和圆度误差进行评定。
(3)交互模块主要是为了用户可以简单的变更参数设置,从而通过图像结果显示可以直观的看到误差分离结果。
3 实验研究与数据处理
对机床主轴进行实验分析,得到3个位移传感器的测量数据,由于测得的实验数据计算较为复杂,用设计的测试系统对实验数据后处理,得到误差分离图像。主轴转速为2 000 r/min,取采样点数N=64,图7a为被测主轴轮廓上不同采样点的圆度误差位移量变化、图7b为分离后的圆度误差。图8a为不同采样点的回转误差数据、图8b为分离后的回转误差圆图像。同一主轴在不同转速下的回转误差见表1。
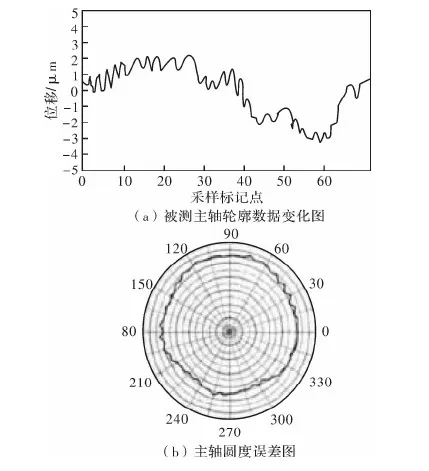
图7 测量数据与圆度误差分离
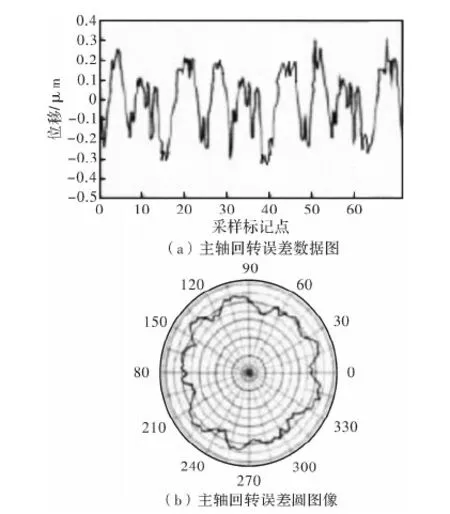
图8 测量数据与回转误差运动分离
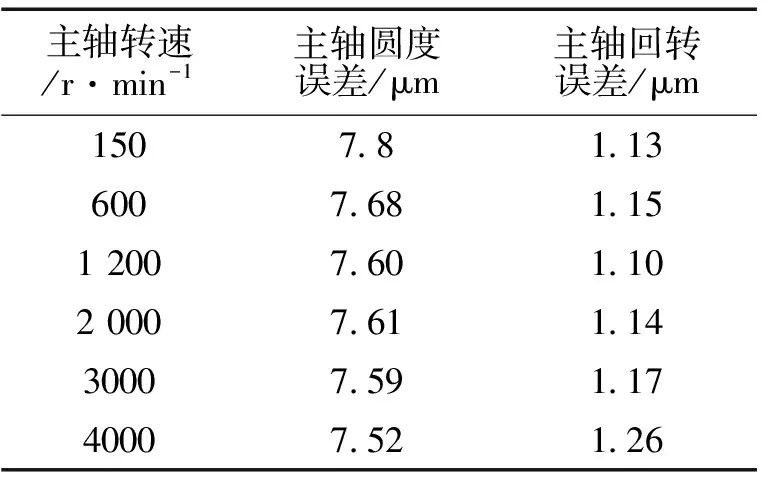
主轴转速/r·min-1主轴圆度误差/μm主轴回转误差/μm1507 81 136007 681 1512007 601 1020007 611 1430007 591 1740007 521 26
4 结束语
本文采用多探头法的—矩阵算法对主轴回转误差进行分离,在此基础上搭建了主轴回转精度测试系统,并进行了试验验证,得到的结果表明:同一主轴,在不同转速条件下,测得的主轴圆度误差基本一致,而主轴回转误差则是随着转速的降低而减小。这是由于主轴速度增加时,主轴运动不平衡引起的误差成分造成的,符合实际测量情况。由此可以得出使用多探头法的矩阵算法误差分离技术能够较准确、有效地分离出主轴回转误差。
致谢:本文得到辽宁省教育厅科研项目“基于柔体力学的复杂曲面砂带磨削机理研究”(No.LGD2016022)的支持。
[1] 陈长浩. 主轴运动精度的测试与研究[D]. 北京:北京工业大学,2010.
[2] 王世良. 超精密车床主轴回转误差测试系统的研究[D]. 哈尔滨:哈尔滨工业大学,2015.
[3] 李超. 基于误差分离技术的精密回转及直线运动部件精度测量[D]. 哈尔滨:哈尔滨工业大学,2010.
[4] 丁国清. 基于误差分离技术的超精密测量及校正方法研究[D]. 上海:上海交通大学,2012.
[5] 董兆鹏,黄富贵.圆度误差测量及评定方法综述[J].工具技术,2011,45(02):14-18.
[6] 熊诗波,黄长艺.机械工程测试技术基础[M] .北京:机械工业出版社,2006.
[7] Ma Yu-zhen,Wang Xin-hua,Kang Yan-hui, et al. Roundness Measurement and Error Separation Technique[J].Mechanics and Materials,2013,303-306:390-393.
[8] 雷贤卿. 基于误差分离的圆柱度精密测量技术研究[D]. 西安:西安理工大学,2007.
[9] 朱永生,岳鹏飞,闫柯,等.精密主轴动态回转误差的实验研究[J].机床与液压,2015,43(07):18-21.
