结构件焊接温度场和应力应变数值模拟研究进展
2018-01-18,,,,
,,,,
(1.上海交通大学上海市激光制造与材料改性重点实验室,上海200240;2.高新船舶与深海开发装备协同创新中心,上海 200240;3.创斯达科技集团(中国)有限责任公司,江苏南通 226300)
0 前言
焊接是金属材料加工制造中一种重要的材料连接方式,连接可靠性非常高,加工周期较短、加工效率高、易于实现自动化,在工业制造领域的应用非常广泛,是现代制造业中不可或缺的材料连接方法。然而焊接过程相当复杂,涉及到金属材料局部的快速熔化及材料的快速凝固,局部温度的快速升高及冷却导致焊接过程中和焊接后工件内部产生相当大的焊接残余应力以及焊接变形。而焊接过程中产生的残余应力及变形影响着工件的精度和使用性能,降低工件的使用寿命。
此外,在焊接温度场和焊接应力的测量方面,由于焊接过程及之后的冷却凝固过程速度非常快,导致焊接温度场和应力应变的测量与分析相当困难。焊接数值模拟方法的提出与使用为测量分析焊接残余应力和变形提供了一定的参考,特别是结构件焊接过程模拟为焊接工艺及参数、焊接顺序等的制定给予一定的指导。同时,现代计算机技术的发展推动了焊接数值模拟技术的发展,使得研究工作者的工作越来越深入,新方法不断涌现,对焊接方面的实际生产和科研起到了推动作用[1]。
1 有限元法原理
有限元法是古典变分法与分片插值法相结合的产物。它先将全域根据实际情况分成很多个小单元,在单元范围内用低次多项式分片插值,再将它们进行组合,使其能形成全域内的函数,再用以逼近问题的真解。这样不但能避免古典方法寻找基函数的困难,而且不规则剖分与差分方法相比灵活性和适应性更大,应用范围极广,能计算物理和工程中的各种复杂问题。
在焊接中常用的热弹塑性有限元法集合了传热有限元分析过程和结构弹塑性有限元分析过程两个部分,能够较好地反映材料的结构参数、焊接工艺参数以及不同的焊接顺序等因素对焊接残余应力和焊接变形等方面的影响[2]。
2 热源的选取
2.1 Ronsenthal-Rykalin解析式
在Ronsenthal-Rykalin解析式[3]中,热源模型可根据焊接结构件的厚度和尺寸形状将热源简化为点、线、面三种形状的热流简化模型。对于大型焊接结构件,焊接时热量的传导沿着3个方向,因此可以将热源看成点状热源,关系式为
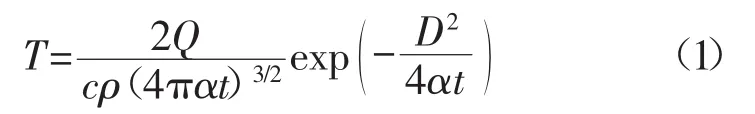
式中 Q为热源中心温度,Q=ηUI;η为焊接热源的效率系数;α为热扩散率;D为距焊接热源中心的距离。
而对于细棒的对接,温度场在细棒的截面上均匀分布,可以将细棒的焊接截面上的各点看成是均温的,因此可以将该焊接热源看成面热源,关系式为

该计算方法以集中热源为基础,假定热物理性能参数不变,不考虑相变与结晶潜热对焊接残余应力应变的影响,将焊接工件的几何形状简单地归为无限长、大、薄,这种模型对于远离焊缝区的计算结果较为精确,但是对于热影响区误差较大。该模型的计算结果虽然精度较差,但是计算过程较为简单,因此在工程上得到广泛应用。
2.2 瞬态移动热源
为了提高计算结果的精度,研究者们参考焊接时的焊接热源分布形状,又提出了高斯热源模型、半球状热源模型、椭球状热源模型及双椭球状热源模型来对应不同情况下的焊接模型。
2.2.1 高斯热源模型
焊接时的焊接热源是通过一定的作用面积将热量传递到焊接工件其他部位,在这个作用面积上热量分布并不均匀,分布规律为中心部位热量最高,边缘部位热量较低。费利德曼将这个作用面积上的热量分布近似地用高斯数学模型进行描述,如图1所示。数学表达式为

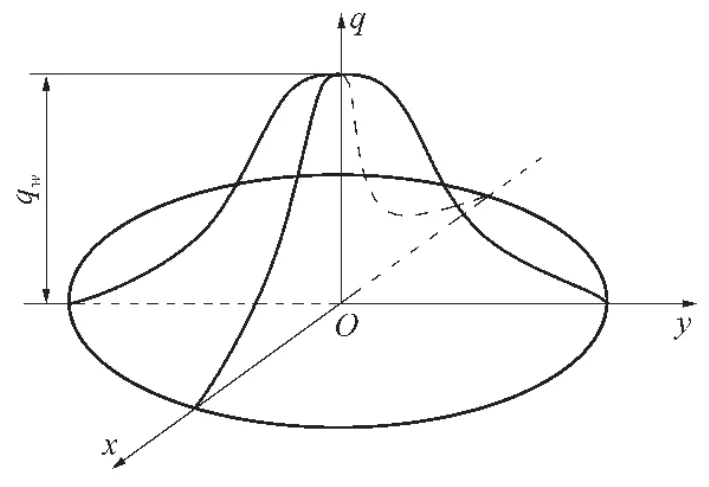
图1 高斯热源的数学模型
式中 r为模型上某一点距离热源中心处的距离;q为距离焊接热源中心r处的热源密度;Qm为热源中心处的最大热源密度;R为焊接热源的有效加热半径。焊条电弧焊、钨极氩弧焊等焊接电弧挺度较小、温度梯度相对较小的焊接方法,运用高斯热源模型能够取得较精确的计算结果。
2.2.2 半球状热源模型与椭球状热源模型
与高斯热源模型相比,半球状热源模型和椭球状热源模型更能适应电弧挺度、温度梯度相对较大的焊接方法,例如高能束焊接。另外考虑到运用激光焊等方法焊接时,焊接熔池并不是球对称的,对于这种情况椭球状热源模型较半球状热源模型更为合适。
半球状热源模型的数学表达式为

椭球状热源模型数学表达式为
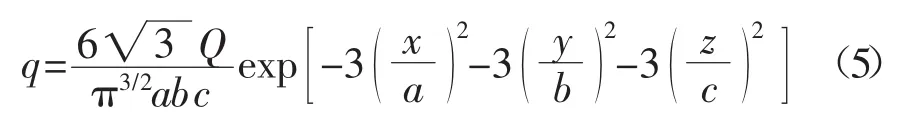
式中 a,b,c分别为在x,y,z轴方向上的半轴长。
2.2.3 双椭球状热源模型
加拿大学者J.Goldak[4]提出的双椭球热源模型是根据椭球热源模型改进而来。在椭球热源模型中,椭球前半部分的温度梯度变化没有实际焊接中剧烈,并且椭球后半部分的温度梯度变化较为平缓,不满足温度梯度和电弧挺度较大的激光焊等焊接特点,因此提出了双椭球热源模型。在双椭球热源模型中,将半侧的椭球分为2个1/4的椭球,前半部分是一个1/4的椭球,后半部分是一个1/4的椭球。前半部分分配的能量系数为n1,后半部分分配的能量系数为n2,n1和n2满足的条件为:n1+n2=1。
前半部分椭球热源模型的数学关系式为
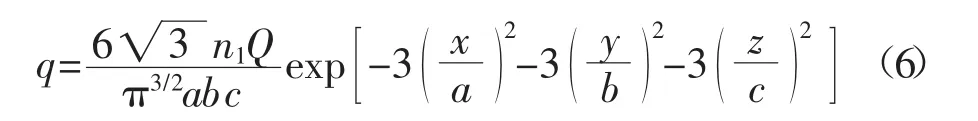
后半部分椭球热源模型的数学关系式为

式中 a,b,c可取不同的值。
通常的焊接方法采用高斯热源;对于电弧冲力较大的熔化极氩弧焊、激光焊接采用双椭球的效果较好,还可以将热源分为两部分,采用高斯分布热源作为表面热源,双椭球分布作为内热源[5]。
2.3 段状热源
除了上述常用热源模型外,研究者们又根据模型的实际情况提出了基于标准几何形状的其他热源模型,使其能够在特定的焊接工艺中取得较好的计算结果。根据计算结果发现,热源的选定对整个模型的计算过程及计算结果有着至关重要的作用,需根据实际情况选取合适的热源模型[6]。
在焊接模拟中,针对瞬态移动热源计算时间过长、计算效率过低的问题,清华大学的鹿安理和蔡志鹏等人[7]提出了高斯分段热源。在高斯分段热源模型中,将焊缝分成若干段,每一段对应一个时间步,每一段内各个点同时施加高斯热量密度,段状热源模型如图2所示。
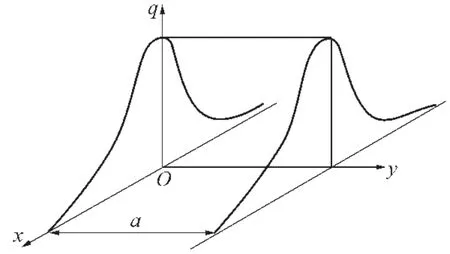
图2 高斯段状热源数学简易模型
这样既减少了点状热源在焊缝上移动所需时间步,大大缩短了计算时间,提高了计算效率,又通过合适的分段数量,保证了模型的计算精度。单位时间高斯热源在作用面上输入热量为
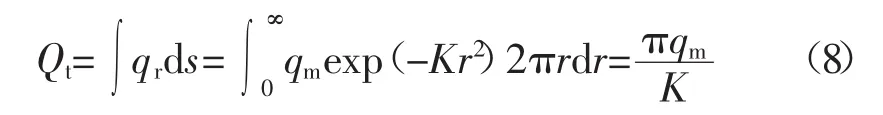
在如图3所示的焊接长度下,高斯段状热源的总输入热量Q的数学表达式为


图3 段状高斯热源数学解析式示意
清华大学的王煜等人[8]将该方法等效地应用于电子束焊的双椭球状热源模型中,计算焊接的残余应力应变,既保证了计算精度,又减少了计算时间,提高了计算效率。
上海交通大学陈震等人[9]认为蔡志鹏等人的分段热源模型中输入的热能密度不随时间变化,总的热能输入量需要对瞬态移动热源的总输入量进行计算求得,因此对其进行改进,特点为:①模型中的各段热能密度输入随着时间变化;②分段热源模型中的热能输入过程与瞬态热源模型一致;③分段热源模型与瞬态热源模型之间可以进行简单地切换,不用再通过复杂的数学积分变换。
3 关于网格划分的优化法
3.1 自适应网格法
自适应网格方法是指计算中在某些变化较为剧烈的区域,如大变形、接触间断面和滑移面等,网格在迭代过程中不断调节,细化网格,做到网格点分布与计算解的调和,从而提高解的精度和效率的一种技术。自适应网格希望在物理解变动较大区域网格自动密集,而在物理解变化平缓区域网格相对稀疏,这样在保持高效率计算的同时可得到高精度的解。自适应网格技术主要有移动网格方法和局部细化或粗化网格方法。近三十年来,自适应网格方法成为网格方法研究的热点问题,在一些领域得到广泛应用。
法国的P.Duranton等人[10]在316L不锈钢的焊接中运用SYSWELD软件进行计算,网格划分方法为自适应网格法,并根据热源模型的特点和热源模型的移动轨迹对网格进行“运动中的重新划分”,如图4所示。

图4 自适应网格法网格划分示意
自适应网格法的提出使得很多复杂工艺的模拟得到实现。在P.Duranton的实验中,自适应网格法得到的结果与实验结果一致,并且计算时间是完全细化网格法所消耗时间的20%。
瑞典的Lindgren L E等人[11]在电子束焊中分别运用h-adaptive自适应网格法和非自适应网格法进行对比计算分析,结果发现使用两种方法得到的计算结果基本相同,但是h-adaptive自适应网格法所需要的计算时间比非自适应网格法缩短了大约60%。
3.2 Shell/3D Solid混合单元法
克罗地亚的Mato Peric等人[12]计算不锈钢EN 10025-2:S355JR的T型接头MAG焊时分别运用Shell/3D Solid混合单元法和实体单元法进行建模,建模方式如图5和图6所示。
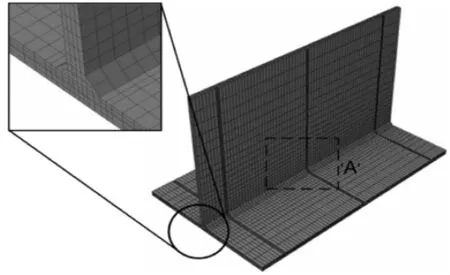
图5 实体单元网格划分示意
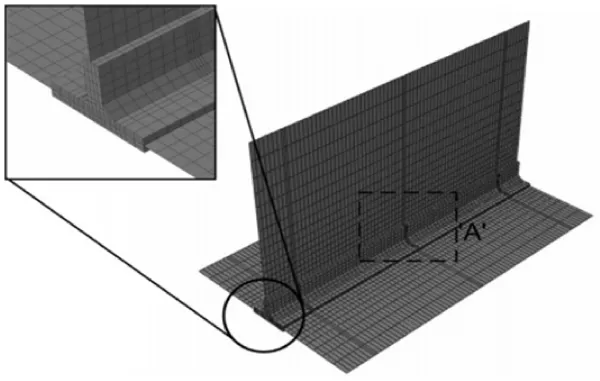
图6 Shell/3D Solid混合单元网格划分示意
Mato Peric等人在壳单元和三维实体单元的交界处用边界约束方程进行约束,约束方程为

式中 Nx、Ny、Nz为法线向边界的方向余弦值;hc和hr分别为对流换热系数和辐射换热系数;qs为边界换热系数;Tr为辐射温度;T∞为室温。
同时,对三维实体单元和混合单元的计算结果进行对比,结果发现,温度场的分布在Shell/3DSolid单元交界处温度梯度过渡平缓,较好地反映出焊接温度场分布,且残余应力应变分布也与纯实体单元模型得到的结果相似。并且采用Shell/3DSolid混合单元法缩短了42%的计算时间。
4 子结构法
将一个大型的复杂结构划分为若干个子结构,先分别确定各子结构的刚度特性,然后将子结构装配成整体结构,最后确定整体结构的刚度特性,这种结构分析方法称为子结构法。采用子结构分析可将一个大型问题化为若干个小问题,将大型的联立方程组分解为若干组小型的方程组,从而减小计算机的内存,实现微机解大题的作用。
某些结构中,材料的形状及应力的变化只集中在局部,其他部位几乎不变,因此将不变部位的结构划分为若干个子结构,变化部位划分为其他的子结构。当结构变化时,只需重新形成变化部分的子结构的刚度矩阵,而不必重新形成全结构的刚度矩阵,从而提高计算效率。
Y.G.Duan等人[13]采用有限元软件SYSWELD计算大型结构件时运用了热弹塑性有限元子结构法,认为焊接引起的塑性应变和金相组织应定位在焊缝附近,可以采用局部三维模型进行确定。对于整体结构,认为整体变形是由于局部的变形所导致,局部塑性应变发生后,作为初始应变然后转移到整体模型中,最后得到整体结构的计算结果。
5 固有应变有限元法
日本学者提出和应用了固有应变ε*的概念,认为焊接固有应变是物体在焊接后存在的塑性应变、温度应变和相变应变三者之和。也可以表征物体在无外力和内应力的情况下,物体从焊接状态恢复到自由状态后,总应变ε减去弹性应变εe的值,即ε*=ε-εe。材料的焊接固有应变是一个随着材料属性、材料尺寸及焊接参数变化的量,在使用焊接固有应变值时需先对它进行测量分析[14]。
日本九州工业大学的Toshio Terasaki等人[15]选用不同的焊接参数对不同厚度的低碳钢板进行平板堆焊的焊接实验,通过测量焊后试样的角变形及横向收缩的大小,得出角变形及横向收缩与焊接线能量和低碳钢板厚度的关系曲线,如图7、图8所示。
上海交通大学的魏良武博士[16]通过焊接变形实验和热弹塑性有限元法测量材料的固有应变,定量分析固有应变与主要影响因素的关系。在SM400A钢中,得到关于横向固有应变系数ξ、纵向固有应变K与输入热量的关系式。
参数为:板宽300 mm,板长300 mm,板厚1.5~40 mm,热量200~500 J/mm,焊接速度10 mm/s。
其关系式为

图7 热输入参数对角变形的影响

图8 热输入参数对横向收缩的影响

重庆交通大学的张继翔教授等人[17]分析T型焊接接头的双侧同步焊接固有应变分布,得到在不同的参数下固有应变的变化趋势为:
(1)在焊缝方向上的横向收缩的变化趋势是先增大后减小,且在焊缝的两端由于焊缝端部效应,产生的横向固有应变高于焊缝其他部位。
(2)在焊缝方向上的纵向固有应变的变化趋势为沿焊缝方向由两端向中间逐渐减小。
(3)T型接头的腹板厚度和翼板厚度对固有应变的影响较大,这是由于随着板厚的增加,材料对焊接变形的抗性增大,因此变形减小,固有应变减小。
(4)随着焊接速度的增大,固有应变随之减小,这是由于随着焊接速度的增大,焊接线能量减小导致焊接变形减小,因此固有应变减小。
(5)腹板宽度和翼板宽度对材料焊接固有应变的影响较小。
重庆交通大学的张继翔教授运用固有应变有限元法计算分析大型桥梁钢箱梁焊接,验证了固有应变有限元法的可行性。
合肥工业大学的李萌盛[18]运用初应变法和初应力法研究低碳钢T型焊接接头,发现固有应变有限元法中的初应力法和初应变法所得结果与热弹塑性有限元法所得结果基本吻合,运用固有应变有限元法可以计算大型薄壁结构件的焊接变形,并且大大减少计算时间,提高计算效率,而且在运用固有应变有限元法时可以运用壳单元代替实体单元进行计算,进一步缩短计算时间。
6 结论
相较以前的经验公式等方法,计算机数值模拟方法能提供更有力的理论指导,计算机的发展与普及也为数值模拟提供了更方便的物质条件。国内外的研究者们针对焊接计算模拟方面的难点及不足之处提出并运用了很多优化方法,除了分段热源法、子结构法、固有应变法和混合单元法,还有平行计算法等其他常用方法,使得数值模拟技术为工业生产与科学研究提供更有力的指导。
但是,现在的焊接过程模拟工作还存在很多问题需要解决,比如:(1)高温下材料的热物理性能参数的缺乏。这是由于实验设备方面的限制,无法彻底解决,并且材料热力学参数的确定过程也较为复杂,得到的参数可能会与材料本身的参数存在一定误差。(2)焊接电弧的有效功率系数难以确定。(3)材料焊接时的相变过程难以处理。
[1]谢元峰,肖汉斌.基于ANSYS的焊接温度场和应力的数值模拟研究[D].武汉:武汉理工大学,2006.
[2]商跃进.有限元原理与ANSYS应用指南[M].北京:清华大学出版社有限公司,2005.
[3]Teng T L,Fung C P,Chang P H,et al.Analysis of residual stresses and distortions in T-joint fillet welds[J].International Journal of Pressure Vessels and Piping,2001,78(8):523-538.
[4]Goldak J,Chakravarti A,Bibby M.A new finite element model for welding heat sources[J].Metallurgical and Materials Transactions B,1984,15(2):299-305.
[5]陈家权,肖顺湖,杨新彦,等.焊接过程数值模拟热源模型的研究进展[J].装备制造技术,2005(3):10-14.
[6]高耀东,张福宽,高俊萍.利用不同焊接热源模型对结构件进行焊接模拟[J].内蒙古科技大学学报,2013(1):59-63.
[7]蔡志鹏,赵海燕,鹿安理,等.焊接数值模拟中分段移动热源模型的建立及应用[J].中国机械工程,2002,13(3):208-210.
[8]吴甦,赵海燕,王煜,等.高能束焊接数值模拟中的新型热源模型[J].焊接学报,2004,25(1):91-94.
[9]沈济超.大型船体结构焊接变形热弹塑性有限元数值模拟方法研究[D].上海:上海交通大学,2015.
[10]Duranton P,Devaux J,Robin V,et al.3D modelling of multipass welding of a 316L stainless steel pipe[J].Journal of Materials Processing Technology,2004(153):457-463.
[11]Lindgren L E,Haggblad H A,McDill J M J,et al.Automatic remeshing for three-dimensional finite element simulation of welding[J].Computer Methods in Applied Mechanics and Engineering,1997,147(3-4):401-409.
[12]Peric M,Tonkovic Z,Rodic A,et al.Numerical analysis and experimental investigation of welding residual stresses and distortions in a T-joint fillet weld[J].Materials&Design,2014(53):1052-1063.
[13]Duan Y G,Vincent Y,Boitout F,et al.Prediction of welding residual distortions of large structures using a local/global approach[J].Journal of mechanical science and technology,2007,21(10):1700-1706.
[14]罗宇,邓德安,江晓玲,等.热变形的固有应变预测法及实例[J].焊接学报,2006,27(5):17-20.
[15]Terasaki T.Effect of Welding Conditions on Residual Stress Distributions and Welding Deformations in Welded Structure Materials[C]//The Twelfth International Offshore and Polar Engineering Conference.International Society of Offshore and Polar Engineers,2002.
[16]魏良武.固有应变法预测焊接变形的研究及其工程应用[D].上海:上海交通大学,2004.
[17]张继祥,刘紫阳,王智祥,等.桥梁钢结构T型接头双侧同步焊有限元建模[J].电焊机,2014,44(8):77-83.
[18]陈重钧,李萌盛,王成.固有应变法在T型接头焊接变形研究中的应用[J].现代焊接,2012(12):16-18.
