基于蜷曲空间结构的近零折射率声聚焦透镜∗

孙宏祥 方欣 葛勇 任旭东 袁寿其

1)(江苏大学理学院,流体机械工程技术研究中心,镇江 212013)2)(中国科学院声学研究所,声场声信息国家重点实验室,北京 100190)

(2017年8月13日收到;2017年9月14日收到修改稿)

1 引 言

声能量聚焦在医学超声治疗、超声成像及无损检测等领域具有重要的应用价值[1−4],引起了国内外研究人员广泛的关注.随着声子晶体与声超材料的迅猛发展,利用其具有的声负折射率可以设计多种类型的声聚焦透镜.通过逐渐变化声子晶体单元的结构参数,如单元尺寸[5]、弹性模量[6]、单元形状[7]及栅格常数[8]等,可以在垂直于声波传输路径的方向上形成梯度分布的声折射率,实现声聚焦效应,但在低频区域,声子晶体的尺寸较大.声超材料单元尺寸较小,具有较高的负折射率,排列具有不同折射率的声超材料单元,如赫姆霍兹谐振腔[9]、十字结构[10]及蜷曲空间[11,12]等,同样可以获得梯度分布的声折射率,实现小尺寸声聚焦透镜.但其工作机理与单元的共振效应密切相关,工作频带较窄,甚至为单频.利用温度场的梯度分布可以在单一介质(空气)中获得梯度分布的声折射率[13,14],实现宽频带声聚焦效应[15,16].此外,基于柱状空心线性结构的本征模式可以获得完美的声聚焦效应,如单层[17,18]及双层圆柱结构[19],所实现的声聚焦效应在海底信号探测[17]、医学超声治疗[17]及声保密通信[18]等领域具有潜在的应用前景.声学超构表面满足广义的斯涅耳定律[20],可以对声波进行非连续的相位调制,实现对声波传播路径的任意操控[21−24],且具有平面超薄结构与易于集成等优点.基于声波相位调制,研究人员设计出多种新型声聚焦器件,如反射[25]与透射[26]声聚焦透镜、对称艾里束声聚焦透镜[27−29]、五模单元声聚焦透镜[30]、两元相位声聚焦透镜[31]、热声聚焦透镜[32]、阻抗匹配型多组分结构声聚焦透镜[33,34]及声纤维簇聚焦透镜[35]等.

近年来,近零折射率声超材料已成为国际研究热点[36−44],由于其具有高透射性与高声速等特点,声波可以在近零折射率材料(near-zero refractive index material,ZIM)产生隧穿效应,且ZIM具有较强的鲁棒性,即使在材料中嵌入刚性散射体,声波的出射波形与能量依然保持不变.此外,ZIM具有特定的声波方向选择性,通过改变声波传播方向,可以实现声波各种透射性能的切换,如声单向传输透镜[45,46]与声隐身斗篷[47]等.因此,设计基于ZIM的声聚焦透镜,可以具有高聚焦性能及高鲁棒性等优点.

本文采用有限元数值方法,基于ZIM的声波方向选择机理,利用蜷曲空间结构为基本单元进行排列,设计具有特定入射与出射界面的几何结构,调控透射声波的出射方向,实现不同类型入射声波的聚焦效应,并研究透镜内部刚性散射体对声聚焦性能的影响.此外,通过改变近零折射率透镜的出射界面,可以精确地调控声波阵面的形状与方向.

2 物理机理与模型

2.1 ZIM的声波方向选择机理

如图1(a),假设声波I1从空气中入射到ZIM表面,入射角为θ1,透射波T1的折射角为θ2;声波I2从ZIM中入射到空气中,入射角为θ3,透射波T2的折射角为θ4.根据折射定律,在空气与ZIM的交界面处,入射角与透射角满足下列方程:

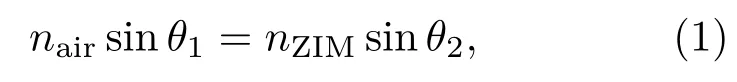
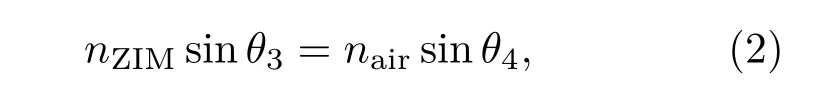
式中nair与nZIM分别为空气与ZIM的折射率.由于nZIM无限接近零,nair不为零,根据(1)与(2)式可得θ1与θ4为零,即当声波垂直入射到ZIM表面(θ1=0°)时,可以透过ZIM,且声波出射方向必定垂直ZIM表面(θ4=0°),如图1(a).

2.2 近零折射率透镜的聚焦机理

基于上述物理机理,设计基于ZIM的声聚焦透镜.当入射声波为平面声源时,如图1(b),聚焦透镜的左侧表面为平面、右侧表面为圆弧面.平面声波水平入射到透镜聚焦左侧表面,由于声传播方向与透镜表面垂直,声波可以透过透镜;而透镜右侧表面为圆弧面,出射声波透过ZIM,垂直于圆弧面,沿其径向传播,声能量汇聚到圆弧面的圆心处,形成明显的声聚焦效应,焦点在圆弧面的圆心处.当入射声波为柱面声源时,如图1(c),聚焦透镜的左右两侧透镜均为相同的圆弧面,柱面声源放置在左侧圆弧面的圆心处,柱面声源激发产生的波阵面与透镜左侧圆弧面符合,因此,入射波阵面上每一点子波传输方向均垂直于透镜左侧圆弧面,声波可以透过透镜,其出射情况与图1(b)相同.

图1 (网刊彩色)(a)ZIM的声波方向选择机理;基于ZIM的(b)平面与(c)柱面声波聚焦透镜Fig.1.(color online)(a)Schematic of direction selection mechanism of acoustic wave in ZIM;schematic of focusing lenses with ZIM for(b)plane and(c)cylindrical acoustic waves.

2.3 近零折射率单元模型及等效介质

为了验证近零折射率聚焦透镜的可行性,引入基于蜷曲空间结构的近零折射率单元,如图2(a).蜷曲空间结构为正方形,由多个黄铜板组成,边长为结构内部黄铜板长度l=0.5934a,厚度w=0.0289a,通道宽度d=0.07a.声波可以在蜷曲空间结构内部的亚波长折叠通道中自由传播,设置不同的结构参数,可以获得不同的声折射率[11],甚至为近零折射率[36,48].本文采用有限元多物理场耦合软件COMSOL Multiphysics数值模拟各种声学性能[49−51],黄铜板的边界设置为声固耦合边界.数值模拟材料参数分别为:黄铜密度ρb=8400 kg/m3、纵波速度cl=4400 m/s、横波速度cs=2200 m/s;空气密度ρair=1.21 kg/m3、声速cair=343 m/s(温度293 K),结构参数a=2 cm.通过计算蜷曲空间结构的反射与透射复系数,可以反演蜷曲空间结构的等效参数[52].图2(b)与图2(c)分别显示蜷曲空间结构的等效密度实部ρr、等效声速绝对值|vr|、等效阻抗实部Zr及声透射率,上述等效参数均为空气参数的相对值.如图2(b)与图2(c),在归一化频率ωa/(2πcair)=0.2128,|vr|可以达到峰值147,ρr几乎为0,透射率与Zr接近于1.因此,蜷曲空间结构等效折射率nr=ρr/Zr接近0,从而获得近零折射率特性.本文以蜷曲空间结构为近零折射率单元,设计近零折射率声聚焦透镜,归一化工作频率为0.2128.

同时,基于蜷曲空间结构的等效参数,构建近零折射率等效介质.等效介质参数设置为ρZIM=ρair/147,cZIM=147cair,其中ρZIM与cZIM分别为相对等效密度与等效声速.等效介质的声阻抗与声折射率分别为ZZIM=ρZIMcZIM与nZIM=1/cZIM,可以得到等效介质的折射率接近于零,且声阻抗与空气声阻抗完全匹配.

图2 (网刊彩色)(a)蜷曲空间结构示意图;(b)蜷曲空间结构的相对等效密度实部ρr(红实线)与相对等效声速绝对值|vr|(蓝虚线);(c)声透射率(红实线)和相对等效声阻抗实部Zr(蓝虚线)与归一化频率的关系Fig.2.(color online)(a)Schematic of coiling-up-space structure;(b)real part of relative density ρr(red solid line)and absolute value of relative acoustic velocity|vr|(blue dashed line);(c)transmission(red solid line)and real part of relative acoustic impedance Zr(blue dashed line)as functions of normalized frequency.

3 近零折射率透镜聚焦性能

3.1 平面声源聚焦

当入射声源为平面声波时,采用图2(b)单侧圆弧面结构.图3(a)—(c)分别显示平面声波通过蜷曲空间结构聚焦透镜、等效介质聚焦透镜及自由空间中的声压空间分布,平面声源位于模型的左侧边界.如图3(a),聚焦透镜由蜷曲空间结构叠加形成,左侧为平面,右侧为圆弧面,其对应的半径为28.3 cm.平面声波可以通过蜷曲空间结构聚焦透镜,并在其圆弧面右侧形成明显的聚焦效应.图3(b)为等效介质聚焦透镜对应的声聚焦性能,聚焦透镜的轮廓尺寸与图3(a)相同,可以看出,在其圆弧面的右侧同样形成明显的聚焦效应,且与图3(a)的聚焦效应基本符合,从而验证了蜷曲空间结构聚焦透镜的正确性.此外,由于等效介质聚焦透镜的右侧圆弧面是光滑连续分布的,而蜷曲空间结构聚焦透镜的右侧表面近似于圆弧面,为不连续分布的,因此,图3(b)中等效介质透镜的声聚焦性能更加完美.在自由空间中,如图3(c),平面声波沿水平方向传播,波形基本不变,无声聚焦现象.图4(a)—(c)分别为图3(a)—(c)对应的声波相位空间分布.如图4(c),在自由空间中,相位波形是一系列不受干扰的竖直波阵面.而有聚焦透镜时,如图4(a)与图4(b),在ZIM的作用下,在透镜右侧,平面声源的相位波形转变为圆弧形,最终汇聚成一个圆形焦点.此外,如图3(a)、图3(b)、图4(a)及图4(b),聚焦透镜左侧的入射声波波形保持完好,说明近零折射率聚焦透镜的反射率几乎为0,表现出完美的声阻抗匹配.

为了进一步表征透镜的声聚焦性能,分别计算经过焦点的横向与纵向声能量密度分布(图3(a)虚线I与II),同时给出平面声波在自由空间激发对应的声能量密度进行比较,并采用焦点处声能量密度最大值进行归一化.如图5(a)和图5(b),在焦点中心(34.7 cm,28.3 cm)处,横向与纵向的声能量密度达到峰值,声能量密度约为自由空间的5倍,聚焦透镜具有良好的声聚焦性能.此外,焦点的中心位置与透镜右侧圆弧面的圆心位置(36.8 cm,28.3 cm)接近,从而进一步验证声聚焦效应由近零折射率特性引起.

图3 (网刊彩色)平面声波通过(a)蜷曲空间结构聚焦透镜、(b)等效介质聚焦透镜及(c)自由空间产生的声压空间分布Fig.3.(color online)Spatial distributions of pressure fi eld through focusing lenses with(a)coiling-up space,(b)equivalent medium,and(c)free space for plan acoustic wave incidence.

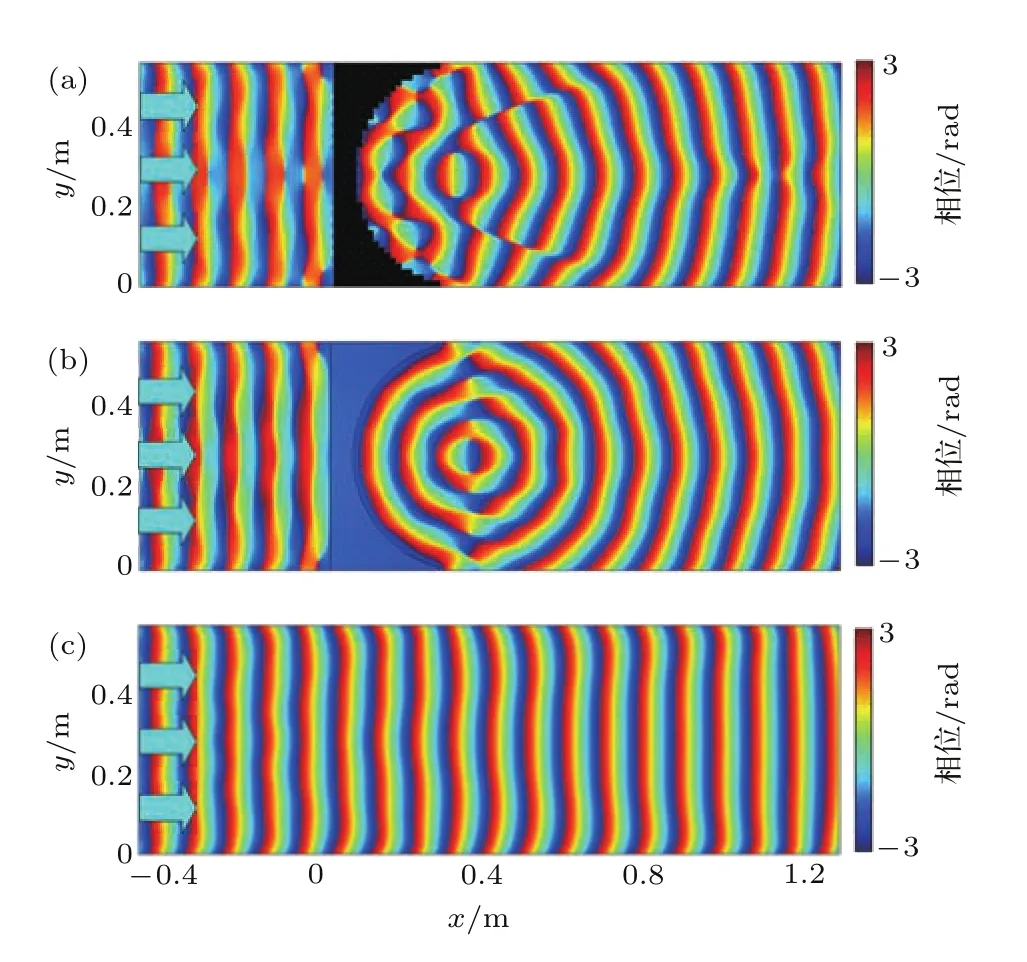
图4 (网刊彩色)平面声波通过(a)蜷曲空间结构聚焦透镜、(b)等效介质聚焦透镜及(c)自由空间产生的相位空间分布Fig.4.(color online)Spatial distributions of phase fi eld through focusing lenses with(a)coiling-up space,(b)equivalent medium,and(c)free space for plan acoustic wave incidence.

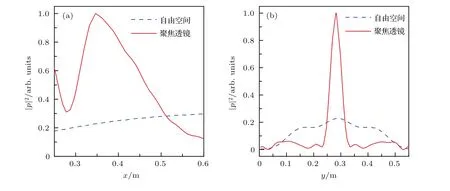
图5 (网刊彩色)经过焦点的(a)横向与(b)纵向归一化声能量密度分布(图3(a)中线I与II)Fig.5.(color online)Normalized acoustic intensity distributions along a line passing through focus(a)in the horizontal direction and(b)in the vertical direction(shown as lines I and II in Fig.3(a)).

3.2 柱面声源聚焦

当入射声源为柱面声波时,采用图2(c)双侧圆弧面结构.图6(a)—(c)分别为柱面声波通过蜷曲空间结构聚焦透镜、等效介质聚焦透镜及自由空间中的声压空间分布,柱面声源位于左侧圆弧面的圆心(−4.2 cm,28.3 cm)处.如图6(a),柱面声波可以透过蜷曲空间结构聚焦透镜,透射声能量沿右侧圆弧面的径向传播,形成明显的聚焦效应.然而,入射声波波形出现明显的干涉现象,这主要由于聚焦透镜左侧圆弧面的几何不规则引起的声能量反射.在等效介质透镜中,如图6(b),入射波形与透射波形几乎没有影响,这主要由于透镜左右两侧均为完美的圆弧面.在自由空间中,柱面声源的圆弧波阵面几乎不受影响,无聚焦效应,如图6(c).图7(a)—(c)分别为图6(a)—(c)对应的声波相位空间分布,基于相位空间分布图,同样可以看出声聚焦性能.

图8为经过焦点的横向与纵向声能量密度分布(图6(a)线I与线II),同时给出平面声波在自由空间激发对应的声能量密度进行比较,并采用焦点处声能量密度的最大值进行归一化.可以看出,在焦点中心(55.3 cm,28.3 cm)处,横向与纵向上的声能量密度均达到峰值,声能量密度约为自由空间的12.5倍,说明柱面声源聚焦透镜同样具有良好的声聚焦性能.此外,焦点的中心位置与透镜右侧圆弧面的圆心位置(56.6 cm,28.3 cm)接近,因此,在实际应用中,可以通过改变透镜与入射声源的位置调节焦点的位置.

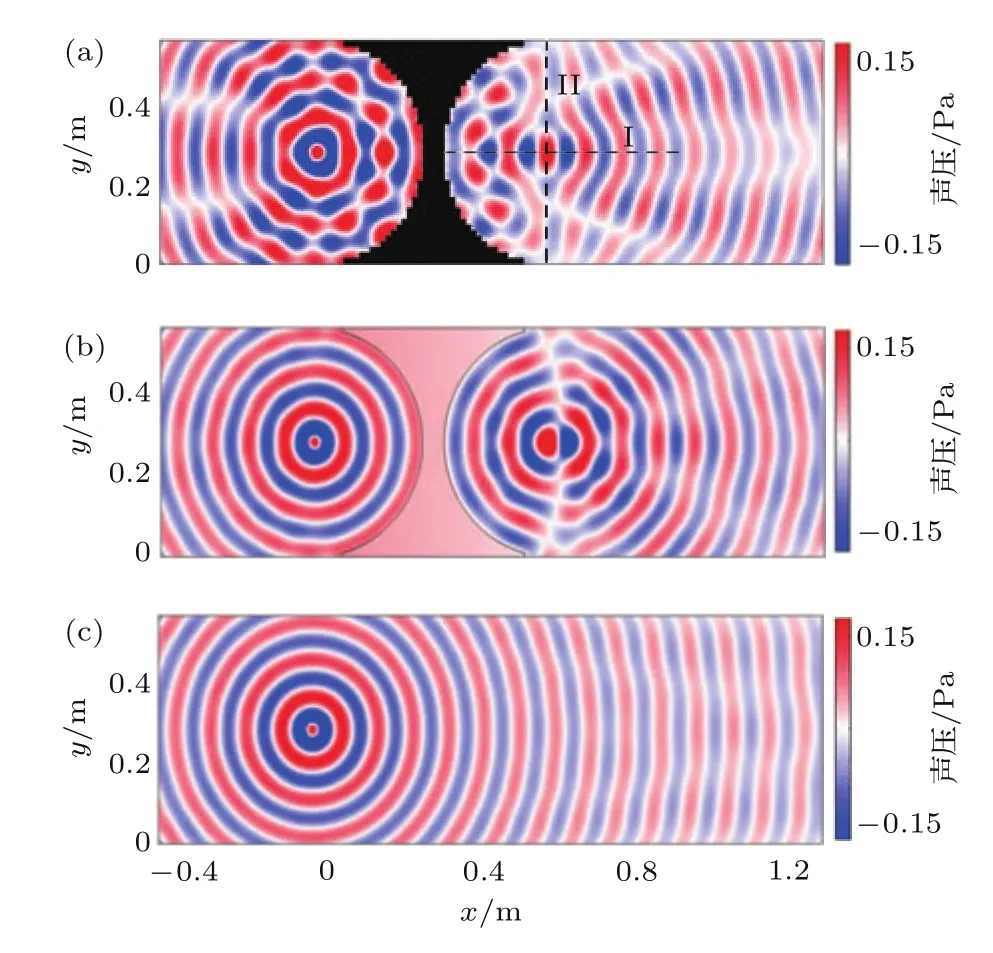
图6 (网刊彩色)柱面声波通过(a)蜷曲空间结构聚焦透镜、(b)等效介质聚焦透镜及(c)自由空间产生的声压空间分布Fig.6.(color online)Spatial distributions of pressure fi eld through focusing lenses with(a)coiling-up space,(b)equivalent medium,and(c)free space for cylindrical acoustic wave incidence.

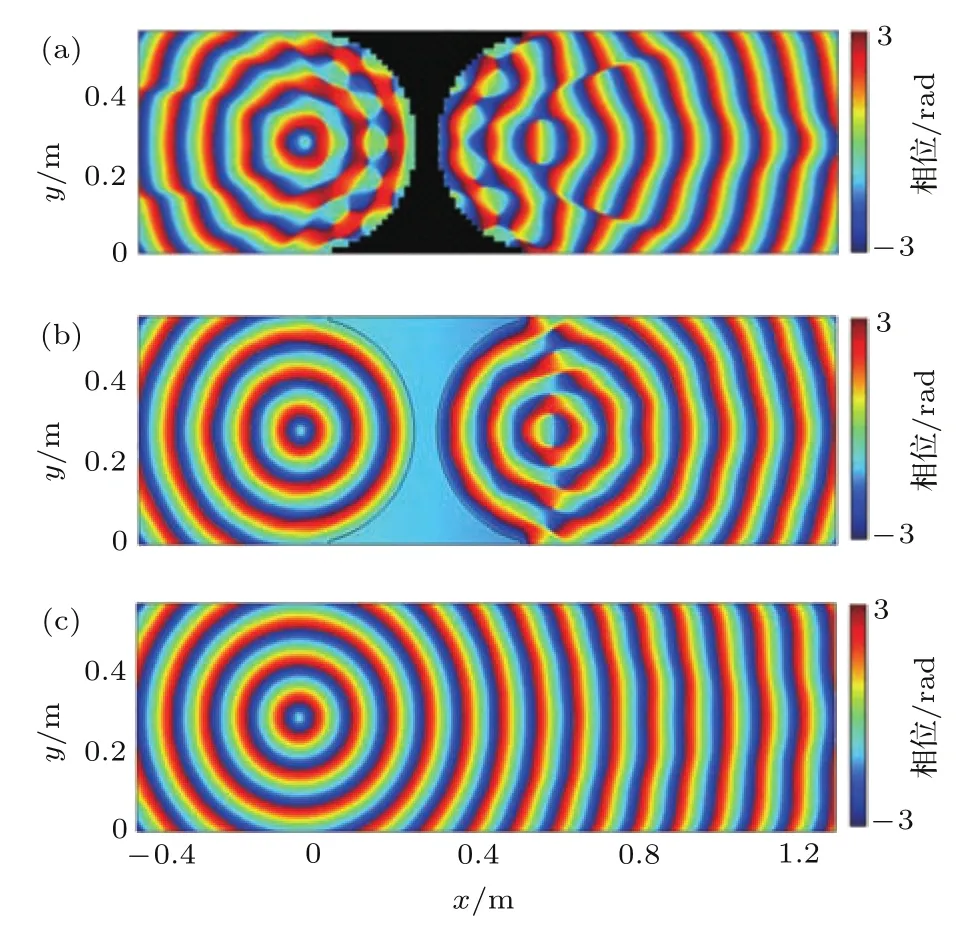
图7 (网刊彩色)柱面声波通过(a)蜷曲空间结构聚焦透镜、(b)等效介质聚焦透镜及(c)自由空间产生的相位空间分布Fig.7.(color online)Spatial distributions of phase fi eld through focusing lenses with(a)coiling-up space,(b)equivalent medium,and(c)free space for cylindrical acoustic wave incidence.

图8 (网刊彩色)经过焦点的(a)横向与(b)纵向归一化声能量密度分布(图6(a)中线I与线II)Fig.8.(color online)Normalized acoustic intensity distributions along a line passing through focus(a)in the horizontal direction and(b)in the vertical direction(shown as lines I and II in Fig.6(a)).

3.3 透镜内部刚性散射体的影响

在ZIM中,声波等效速度很大,其等效波长远大于材料内部缺陷的尺度,因此,声能量能够绕过缺陷传播不受影响.为了验证该性能,在上述两种声聚焦透镜的内部放入相同的刚性散射体(白色,尺寸为11.3 cm×4.2 cm),研究刚性散射体对声聚焦性能的影响.如图9(a),平面声波能够绕过透镜内部的刚性散射体,在圆弧面右侧形成明显的声聚焦效应,与图3(a)结果相比,聚焦透镜嵌入刚性散射体对应的声聚焦性能几乎不变.如图9(b),柱面声波同样能够绕过聚焦透镜内部的刚性散射体,产生明显的声聚焦效应,且与无刚性散射体的结果(图6(a))相比,声聚焦性能同样不变.

图10为经过焦点的横向声能量密度分布(图9(a)线I与线II),同时给出透镜内部无散射体对应的声能量密度分布进行比较,并采用有散射体对应的声能量密度最大值进行归一化.与图9结果类似,两种声聚焦透镜产生的横向声能量密度分布符合很好,从而进一步说明透镜刚性散射体对透镜的声聚焦性能影响很小.因此,与其他类型声聚焦透镜相比,基于蜷曲空间结构的近零折射率聚焦透镜具有较好的鲁棒性.

图9 (网刊彩色)(a)平面与(b)柱面声波聚焦透镜内置刚性散射体的声压空间分布Fig.9.(color online)Spatial distributions of pressure fi eld in focusing lenses for(a)plan and(b)cylindrical acoustic waves with built-in rigid scatterers.

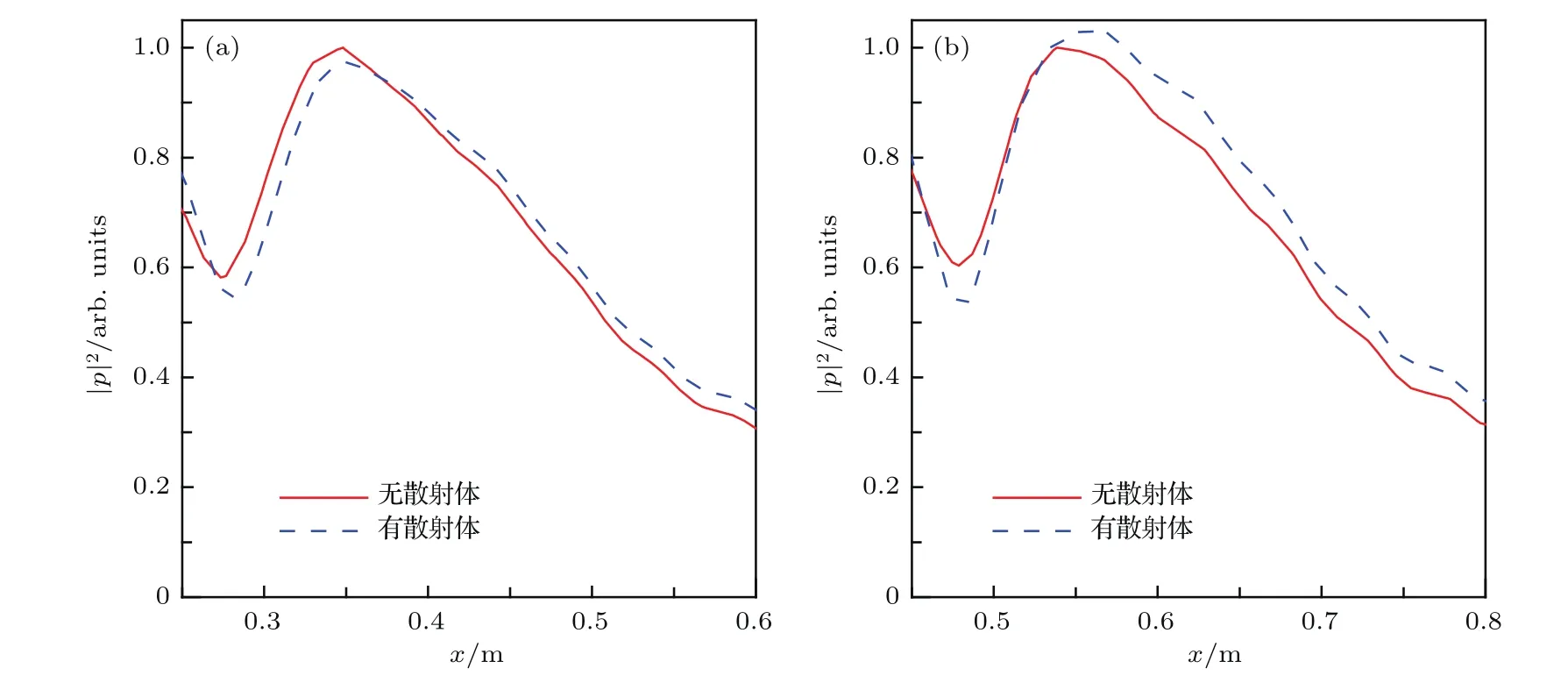
图10 (网刊彩色)(a)平面与(b)柱面声波聚焦透镜经过焦点的横向归一化声能量密度分布(图9(a)中线I与线II)Fig.10.(color online)Normalized acoustic intensity distributions along a line passing through focus in the horizontal direction for(a)plan and(b)cylindrical acoustic waves with built-in rigid scatterers(shown as lines I and II in Fig.9(a)).

4 近零折射率透镜的声波阵面调控机理

在实现声聚焦效应的基础上,通过调节透镜出射界面的几何结构,还可以实现声波阵面的调控,如图11(a),近零折射率透镜左侧为圆弧面,右侧为竖直平面.柱面声源放置在左侧圆弧面的圆心处,通过右侧平面进行调控,可以将柱面声波的波阵面转化为平面声波的波阵面.此外,如图11(b),当近零折射率透镜右侧为倾斜平面时,倾角为α,所形成的透射声波的传播方向同样发生改变,其偏转角度为β=90°−α.

为了验证该性能,采用图11(a)右侧竖直平面结构.如图12(a),柱面声源放置在左侧圆弧面的圆心处,柱面声波的波阵面与入射圆弧面符合,声波透过透镜,透射声波的出射方向垂直于右侧平面,从而以平面声波的波阵面形式水平向右传播.图12(b)为等效介质透镜对应的声压空间分布,可以看出,当左侧圆弧面为光滑连续分布时,透镜的声阻抗与空气声阻抗完全匹配,声透射率很高,因此,该波阵面调控方式具有高透射性.

在此基础上,采用图11(b)右侧倾斜平面结构.如图13,当透镜右侧平面的倾角α分别为71°,63°,45°及0°时,透射声波同样为平面声波波阵面,但其传播方向(黑色空心箭头)的偏转角度β分别对应为19°,27°,45°及90°,说明该透镜可以将柱面声波调控为任意传播角度的平面声波.基于上述结果,近零折射率透镜不仅可以实现高性能的声聚焦效应,还可以精确地调控波阵面的形状及方向,为声波调控提供了新机理与新思路.

图11 (网刊彩色)基于ZIM的(a)水平与(b)倾斜波阵面调控透镜Fig.11.(color online)Schematic of the lenses with ZIM for(a)horizontal and(b)inclined wavefront manipulation.

图12 (网刊彩色)水平波阵面调控透镜的声压空间分布 (a)蜷曲空间结构;(b)等效介质Fig.12.(color online)Spatial distributions of pressure fi eld for the lenses of horizontal wavefront manipulation with(a)coiling-up space and(b)equivalent medium.

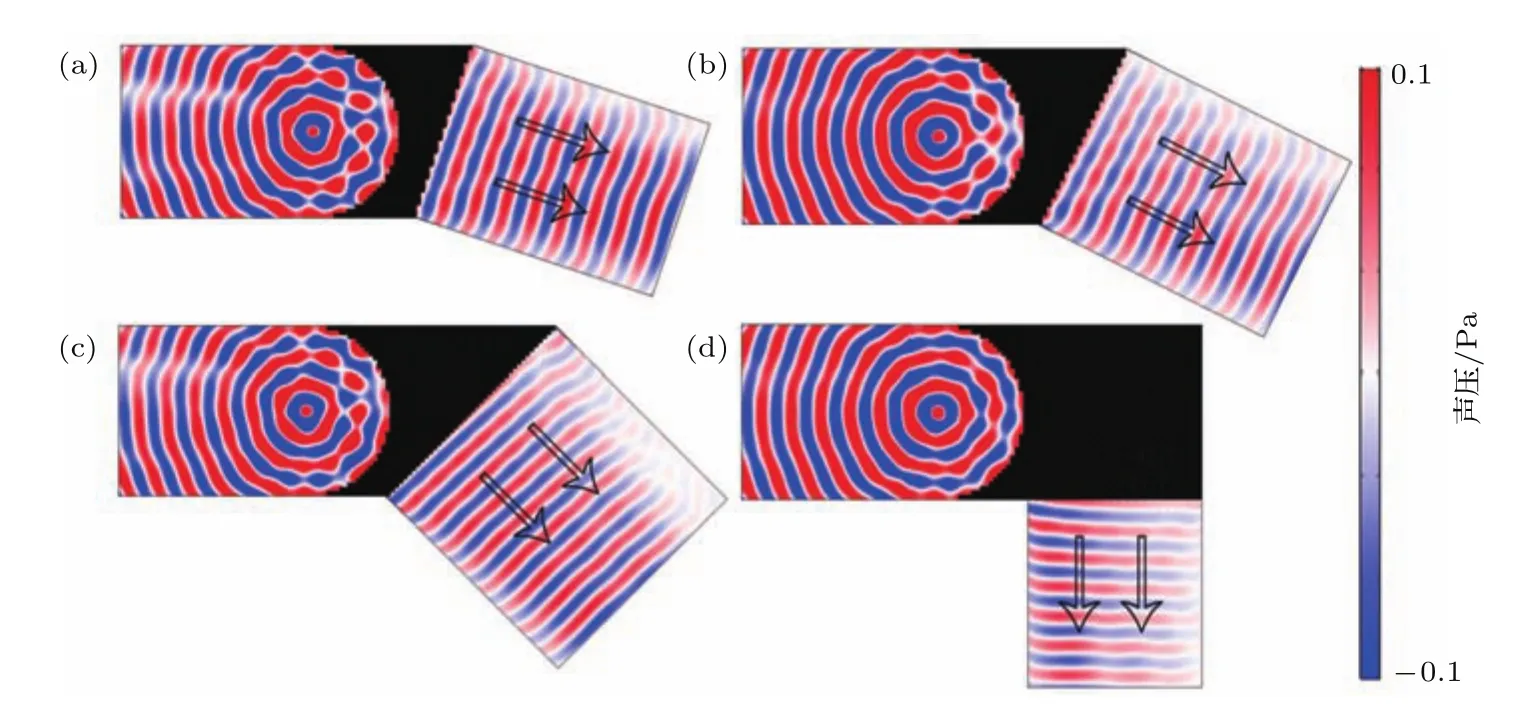
图13 (网刊彩色)倾角为(a)α=71°,(b)α=63°,(c)α=45°及(d)α=0°波阵面调控透镜的声压空间分布,黑色空心箭头表示声波的透射方向Fig.13.(color online)Spatial distributions of pressure fi eld for the lenses of wavefront manipulation with inclined angles(a)α =71°,(b)α =63°,(c)α =45°,and(d)α =0°.Black hollow arrows indicate the transmitted direction of acoustic waves.

5 结 论

本文基于ZIM的声波方向选择机理,采用蜷曲空间结构为基本单元进行排列,设计具有特定入射与出射界面的几何结构,实现了平面声波与柱面声波的聚焦效应.研究结果表明:入射面与出射面分别为平面与圆弧面的透镜可以实现平面声波聚焦效应;入射面与出射面均为圆弧面的透镜可以实现柱面声波聚焦效应;近零折射率透镜内部的刚性散射体对聚焦性能没有影响.此外,入射面与出射面分别为圆弧面与平面的透镜可以将柱面声波转化为平面声波,且改变出射平面的倾角可以调控平面波的传播方向.基于蜷曲空间结构透镜与等效介质透镜的模拟结果基本一致.与其他类型的声聚焦透镜相比,近零折射率声聚焦透镜具有单一单元结构、高聚焦性能及高鲁棒性等优点.研究结果为设计新型近零折射率声聚焦透镜提供了理论指导与实验参考,同时也为研究声波阵面的调控提供了新思路.

[1]Zhao J J,Ye H P,Huang K,Chen Z N,Li B W,Qiu C W 2014Sci.Rep.4 6257

[2]Gu Y,Cheng Y,Liu X J 2015Appl.Phys.Lett.107 133503

[3]Zheng L,Guo J Z 2016Acta Phys.Sin.65 044305(in Chinese)[郑莉,郭建中 2016物理学报65 044305]

[4]Tang K,Qiu C Y,Lu J Y,Ke M Z,Liu Z Y 2015J.Appl.Phys.117 024503

[5]Deng K,Ding Y Q,He Z J,Zhao H P,Shi J,Liu Z Y 2009J.Phys.D:Appl.Phys.42 185505

[6]Lin S C S,Huang T J,Sun J H,Wu T T 2009Phys.Rev.B79 094302

[7]Torrent D,Sánchez-Dehesa J 2007New J.Phys.9 323

[8]Peng S S,He Z J,Jia H,Zhang A Q,Qiu C Y,Ke M Z,Liu Z Y 2010Appl.Phys.Lett.96 263502

[9]Zhang S,Yin L L,Fang N 2009Phys.Rev.Lett.102 194301

[10]Zigoneanu L,Popa B I,Cummer S A 2011Phys.Rev.B84 024305

[11]Li Y,Liang B,Tao X,Zhu X F,Zou X Y,Cheng J C 2012Appl.Phys.Lett.101 233508

[12]Wang W Q,Xie Y B,Konneker A,Popa B I,Cummer S A 2014Appl.Phys.Lett.105 101904

[13]Dehesa J S,Angelov M I,Cervera F,Cai L W 2009Appl.Phys.Lett.95 204102

[14]Qian F,Zhao P,Quan L Liu X Z,Gong X F 2014Europhys.Lett.107 34009

[15]Ge Y,Sun H X,Liu C,Qian J,Yuan S Q,Xia J P,Guan Y J,Zhang S Y 2016Appl.Phys.Express9 066701

[16]Liu C,Sun H X,Yuan S Q,Xia J P 2016Acta Phys.Sin.65 044303(in Chinese)[刘宸,孙宏祥,袁寿其,夏建平2016物理学报65 044303]

[17]Xia J P,Sun H X 2015Appl.Phys.Lett.106 063505

[18]Xia J P,Sun H X,Cheng Q,Xu Z,Chen H,Yuan S Q,Zhang S Y,Ge Y,Guan Y J 2016Appl.Phys.Express9 057301

[19]Guan Y J,Sun H X,Liu S S,Yuan S Q,Xia J P,Ge Y 2016Chin.Phys.B25 104302

[20]Yu N,Genevet P,Kats M A,Aieta F,Tetienne J P,Capasso F,Gaburro Z 2011Science334 333

[21]Li Y,Liang B,Gu Z M,Zou X Y,Cheng J C 2013Sci.Rep.3 2546

[22]Mei J,Wu Y 2014New J.Phys.16 123007

[23]Tang K,Qiu C Y,Ke M Z,Lu J Y,Ye Y T,Liu Z Y 2014Sci.Rep.4 6517

[24]Xie Y,Wang W,Chen H,Konneker A,Popa B I,Cummer S A 2014Nat.Commun.5 5553

[25]Zhu Y F,Zou X Y,Li R Q,Jiang X,Tu J,Liang B,Cheng J C 2015Sci.Rep.5 10966

[26]Yuan B G,Cheng Y,Liu X J 2015Appl.Phys.Express8 027301

[27]Gao H,Gu Z M,Liang B,Zou X Y,Yang J,Yang J,Cheng J C 2016Appl.Phys.Lett.108 073501

[28]Qian J,Liu B Y,Sun H X,Yuan S Q,Yu X Z 2017Chin.Phys.B26 114304

[29]Liu C,Xia J P,Sun H X,Yuan S Q 2017J.Phys.D:Appl.Phys.50 505101

[30]Tian Y,Wei Q,Cheng Y,Xu Z,Liu X J 2015Appl.Phys.Lett.107 221906

[31]Fan X D,Zhu Y F,Liang B,Yang J,Cheng J C 2016Appl.Phys.Lett.109 243501

[32]Liu C,Sun H X,Yuan S Q,Xia J P,Qian J 2017Acta Phys.Sin.66 154302(in Chinese)[刘宸,孙宏祥,袁寿其,夏建平,钱姣2017物理学报66 154302]

[33]Jahdali R A,Wu Y 2016Appl.Phys.Lett.108 031902

[34]Wang X P,Wan L L,Chen T N,Song A L,Wang F 2016J.Appl.Phys.120 014902

[35]Xia J P,Sun H X,Yuan S Q 2017Sci.Rep.7 815

[36]Liang Z X,Li J 2012Phys.Rev.Lett.108 114301

[37]Xie Y B,Popa B I,Zigoneanu L,Cummer S A 2013Phys.Rev.Lett.110 175501

[38]Li Y,Wu Y,Mei J 2014Appl.Phys.Lett.105 014107

[39]Cheng Y,Zhou C,Yuan B G,Wu D J,Wei Q,Liu X J 2015Nat.Mater.14 1013

[40]Lu G X,Ding E L,Wang Y Y,Ping X Y,Cui J,Liu X Z,Liu X J 2017Appl.Phys.Lett.110 123507

[41]Wang Z Y,Wei W,Hu N,Min R,Pei L,Chen Y W,Liu F M,Liu Z Y 2014J.Appl.Phys.116 204501

[42]Gu Y,Cheng Y,Wang J S,Liu X J 2015J.Appl.Phys.118 024505

[43]Liu F M,Liu Z Y 2015Phys.Rev.Lett.115 175502

[44]Wu S Q,Mei J 2016AIP Adv.6 015204

[45]Li Y,Liang B,Gu Z M,Zou X Y,Cheng J C 2013Appl.Phys.Lett.103 053505

[46]Shen C,Xie Y B,Li J F,Cummer S A,Jing Y 2016Appl.Phys.Lett.108 223502

[47]Zheng L Y,Wu Y,Ni X,Chen Z G,Lu M H,Chen Y F 2014Appl.Phys.Lett.104 161904

[48]Xie Y B,Konneker A,Popa B I,Cummer S A 2013Appl.Phys.Lett.103 201906

[49]Sun H X,Zhang S Y,Yuan S Q 2016Chin.Phys.B25 124313

[50]Jia D,Sun H X,Yuan S Q,Ge Y 2017Chin.Phys.B26 024302

[51]Sun X D,Chen L,Jiang H B,Yang Z B,Chen J C,Zhang W Y 2016IEEE T.Ind.Electron.63 3479

[52]Fokin V,Ambati M,Sun C,Zhang X 2007Phys.Rev.B76 144302