基于机会蚂蚁群集的多频段融合GPS弱信号跟踪采集

,, ,

(1.太原理工大学 电气与动力工程学院,太原 030024;2.煤矿电气设备与智能控制山西省重点实验室,太原 030024;3.山西太原天地方圆电子科技有限公司,太原 030024)

0 概述

GPS是目前应用最广泛的一种卫星导航系统,在煤矿安全[1]、现代化工业制造、运输和社会生活[2]等各个行业领域对定位与导航的依赖性越来越强,而GPS担任着重要角色,正发挥着关键作用。

在GPS定位过程中,如何分配资源、控制信号传输过程以便提供定位精度成为关键因素之一。文献[3]将蚂蚁算法应用于动态虚拟仿真建模,结合指引因子蚂蚁算法提出了一种的可行的有效的仿真资源分配方案。文献[4]针对高速无线网络的用户规模对资源分配和信号传输的制约问题,提出了一个独特的蚁群优化方法,可以有效连续消除干扰。但是上述文献的蚂蚁算法的复杂度和自适应能力并未得到深入分析。文献[5]提出基于连通性保持的分布式群集控制协议,该协议不仅光滑有界有效消除了抖振现象,而且基于群集控制实现了目标个体运动和系统拓扑管理。因此,群集系统与分群运动相结合[6], 进行目标运动建模和管理控制成为有效解决方案。为了消除二阶多自主体系统的干扰,文献[7]基于个体局部信息,研究一种分布式控制协议。该协议可以在外界干扰的环境中依然满足领航者自主群体群集运动同步条件。

在GPS定位与跟踪应用中,弱信号是约束GPS信号检测与采集的重要因素。文献[8]的弱信号恢复方法充分发挥三维曲波变换传统的优势,有效解决了强噪声环境的弱信号检测与修复问题。但是,随着GPS信号强度的降低,容易被噪声淹没,因此,文献[9]借助杜芬振子及其高敏感特性,建立一种变相位周期策动力杜芬振子弱信号检测方法。该方法很难高效实现多径干扰和恶劣复杂环境 GPS 信号的跟踪,于是文献[10]将码环跟踪鉴相算法与修正因子相结合,实现了多径干扰下 GPS 弱信号的跟踪。文献[11]针对信号漂移现象,通过将长时间压缩感知跟踪与检测相融合,准确捕获复杂或被隐蔽的目标。文献[12]分析了限制相干积分在采集算法由于导航数据位符号化,提出了一种新的并行采集与转换检测算法,以便克服位符号化的局限性。文献[13]通过重新缩放和自适应随机共振,提出了一种新的全球导航卫星系统弱信号捕获方法,解决全球导航卫星系统难以采集高灵敏度信号的问题。然而,GPS信号遇到多径传播时,接收到的波形容易发生扭曲失真,降低信号采集精度,文献[14]将贝叶斯估计和伯努利高斯-拉普拉斯分布相结合,有效提高了GPS信号跟踪敏感度。文献[15]提出了一种空间常见的稀疏基于大规模多输入多输出频分双工自适应信道估计和反馈方案系统,以适应训练开销和导频设计可靠性估计,降低了下行链路的信道状态信息开销。

上述研究成果对于GPS弱信号的提取和多频段对信号检测、采集及跟踪性能的影响未做详细分析,因此,本文建立机会蚂蚁群集网络模型,研究多频段融合模型,从而提出基于机会蚂蚁群集的多频段融合GPS弱信号跟踪采集算法。

1 机会蚂蚁群集模型

基于蚂蚁群集算法为信号检测与跟踪提供元数据时,以下3个关键因素可能会制约蚂蚁个体行为分析精度和群体感知能力:1)时变的信号强度;2)动态的目标轨迹;3)未知的外界干扰和内部信号失真。上述3个方面因素会随着蚂蚁群体状态的变化而不同程度地影响蚂蚁群体规模和蚂蚁个体行为的可识别性,在最坏情况下将严重制约蚂蚁群集性能。

基于上述3个方面因素,根据信号源的时空轨迹和相邻蚂蚁个体状态,以改善蚂蚁群集信号捕捉能力和元数据精度为目标,对蚂蚁群集进行优化和重组。

蚂蚁群集网络系统架构如图1所示。其中,有5个蚂蚁个体目标分别是a、b、c、d、e。2个蚂蚁目标之间的实线箭头表示蚂蚁间有信号传输,并定义了传输方向。2个蚂蚁目标之间的虚线表示蚂蚁间的信号时变轨迹,且信号传输方向未知。hi表示信号输入强度。ho表示信号输出强度,蚂蚁个体目标d和e可以向外拓展,与其他蚂蚁群集建立网络架构。

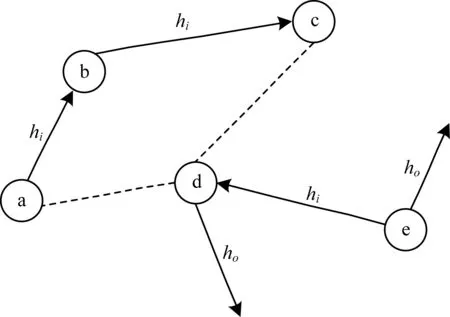
图1 蚂蚁群集系统架构

从信号强度的时变特性和蚂蚁个体动态的目标轨迹角度出发,每个蚂蚁个体的状态表征受到各种外界因素约束和信号失真条件限制,这种限制条件组成了一个蚂蚁群集网络架构多时空、高维度的随机过程。该过程如式(1)所示。

(1)

其中,SC表示蚂蚁群集信号强度,dS表示信号维度,Tt表示信号的时间轨迹,TS表示信号的空间轨迹,Mef表示外界干扰因素矩阵,ML_sd表示信号失真矩阵。

函数Ht(x,y)可以统计蚂蚁群集网络内部信号发送随机序列及信号强度,函数gt(x,y)可以统计蚂蚁群集网络外部信号发送随机序列及信号强度。

由式(1)可以发现,蚂蚁群集信号强度变化具有非线性特征,结合信号时变和蚂蚁个体轨迹变化,发现单个蚂蚁的随机性和蚂蚁群集网络系统状态受到多种因素约束和限制,例如蚂蚁群集所处外界环境、信号轨迹控制等。因此,当信号在蚂蚁群集网络中转发时,任意2个蚂蚁个体根据信号的随机轨迹,可以机会地加入传输路径,以便降低外界干扰因素对函数Ht的影响和信号失真对函数gt的干扰,机会过程控制如图2所示。其中,在信号发送节点与接收节点之间由机会蚂蚁群集网络覆盖。W表示激活状态的蚂蚁个体目标,C表示候选蚂蚁个体目标,实线矩形中是处于工作状态的蚂蚁群集网络,该网络根据式(1),机会地从候选C蚂蚁个体群中选择最佳蚂蚁个体加入新的蚂蚁群集网络,从而形成虚线矩形所示的机会蚂蚁群集网络。

图2 蚂蚁群集机会控制过程

因此,机会蚂蚁群集信号强度SC_O可由式(2)计算得到。

(2)

其中,δ表示外界干扰因素的信号输入机会权重系数,ρ表示信号时变轨迹的信号输出机会权重系数。

2 多频段融合GPS弱信号跟踪采集算法

基于机会蚂蚁群集网络架构的GPS信号频域表征传播过程具有式(3)所示的特点。

(3)

其中,Fq表示各射频频段的上限值,Si表示GPS信号采样样本点功率,SSi表示信号序列,α表示GPS信号与蚂蚁个体目标天线夹角,K表示信号序列长度,n表示样本点数,x(f)表示GPS信号发送强度,y(t)表示机会蚂蚁群集输出信号强度,IS表示GPS信号多频段频域上的信号强度特征,IS[0]表示GPS弱信号频域表征传播过程,将其作为GPS信号跟踪的初始值,可由机会蚂蚁群集的输出信号计算得到。

因此,基于机会蚂蚁群集网络架构的GPS信号频域跟踪流程模型如图3所示。其中,弱信号频域融合可由式(4)结合如图4所示流程加以完成,生成有助于提高GPS弱信号采集和跟踪的弱信号融合体。

图3 频域GPS信号跟踪流程

(4)

其中,SW_F表示弱信号频域融合体,β表示提取弱信号的相位偏移弧度。

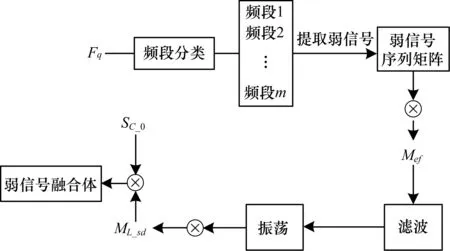
图4 GPS弱信号融合体生成流程

综上,多频段融合GPS弱信号跟踪敏感度ST如式(5)所示。

(5)

其中,根据GPS信号序列长度和样本数的比值,结合频段上限和外界干扰矩阵的秩,判断多频段。采集GPS弱信号形式如式(6)所示。

(6)

其中,R(ML_sd)表示矩阵ML_sd的秩。

3 算法性能分析

仿真实验全面分析了机会蚂蚁群集算法(记为OAC)的平均执行时间,多频段融合GPS弱信号跟踪采集算法(记为MDF)的跟踪精度和信号采集敏感度。同时,机会蚂蚁群集算法的平均执行时间与静态蚂蚁群集算法(记为SAC)进行比对,所提算法的跟踪精度和信号采集敏感度与未提取GPS弱信号的跟踪采集算法(记为NE-WS)进行了比对。

使用 Matlab的Simulink进行GPS信号的建模和仿真,再结合数学分析,验证和测试本文提出算法的性能。仿真GPS信号从“GPSdata-DiscreteComponents-fs38_192-if9_55.bin”中提取得到。在实验中,设定蚂蚁群集的个体数为5～10的随机数,蚂蚁个体间按照如图2所示,根据式(2)建立机会网络架构。GPS发送端的信号漂移轨迹遵循如图3所示约束条件。该信号轨迹近似固定向东南反向以0 m/s～50 m/s的速度直线漂移。蚂蚁群集的整体运动轨迹与 GPS 卫星发送端在二维平面上的方向夹角为10°～35°的随机数。其他实验参数如表1所示。

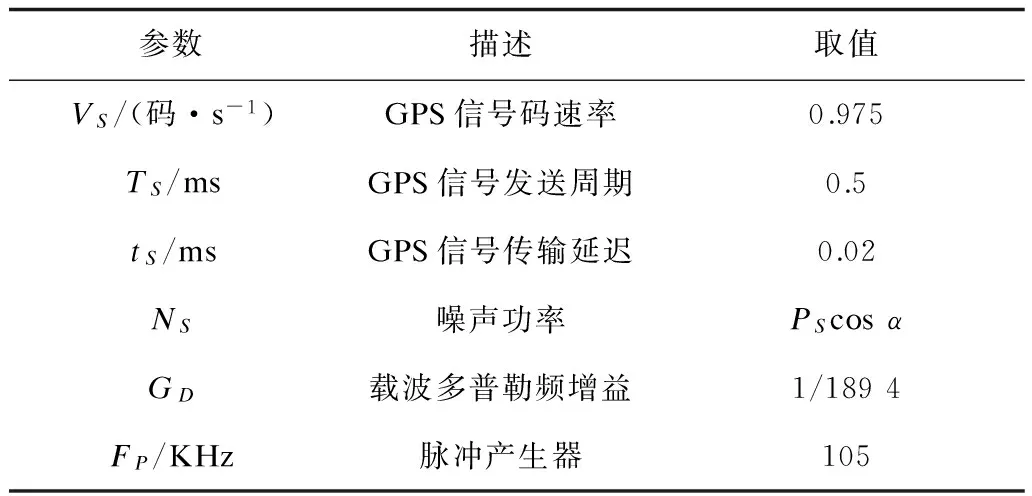
表1 实验参数

其中,PS表示GPS信号功率。GPS弱信号产生模型如式(7)所示。

(7)

图5给出了机会蚂蚁群集算法(记为OAC)与静态蚂蚁群集算法(记为SAC)的平均执行时间对比结果。其中,横坐标是被激活的蚂蚁个体数。从图5中可以发现,蚂蚁群集网络系统在外界干扰因素的信号输入机会权重系数δ和信号时变轨迹的信号输出机会权重系数ρ的机会控制下,不仅可以有效消除外界干扰和准确获得信号漂移轨迹,还具有较高的实时性,为捕获GPS弱信号并进行有效跟踪提供了基础。

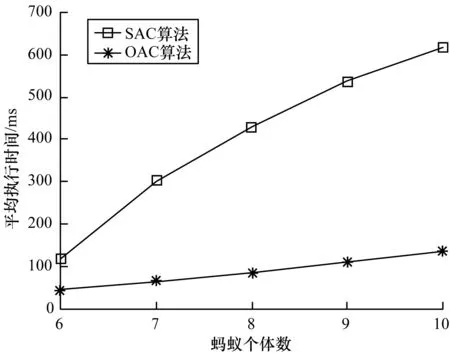
图5 2种算法平均执行时间结果对比

跟踪精度和信号采集敏感度对比结果如图6、图7所示。从图6可以看出,一方面验证了弱信号的存在对GPS信号跟踪采集的影响较为严重,NE-WS算法未有效提取弱信号而使得敏感度急剧下降。敏感度的下降直接导致跟踪精度在食欲上始终处于低谷,如图7所示。然而,MDF算法有效地提取GPS弱信号,并基于多频段加以融合,所以具有高敏感度和跟踪精度。

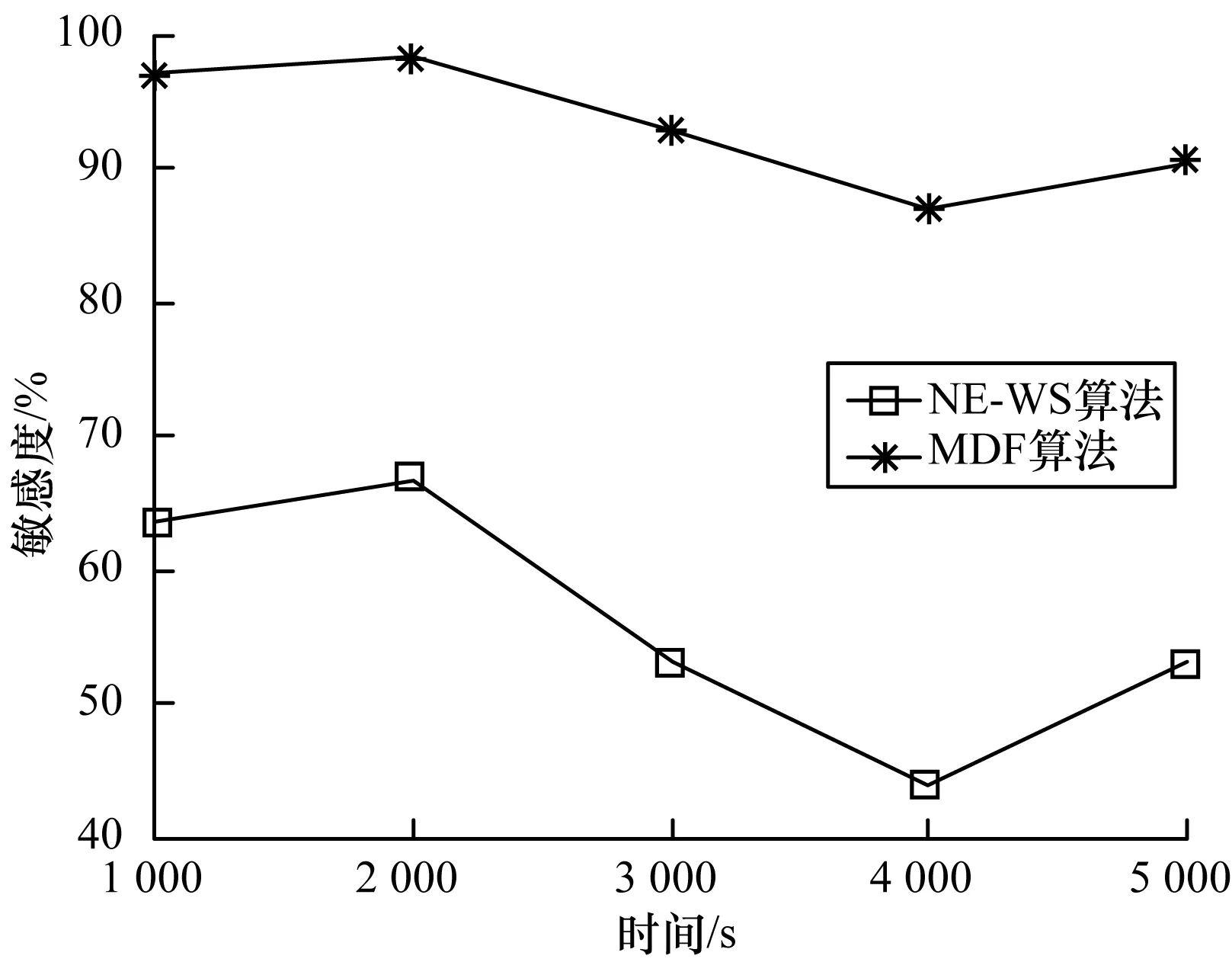
图6 2种算法敏感度结果对比

图7 2种算法跟踪精度结果对比

4 结束语

有效获取GPS弱信号,消除各种噪声干扰和抵消信号失真是改善恶劣复杂环境的GPS定位与跟踪性能的重要保障。本文以蚂蚁群集信号检测与跟踪元数据为研究对象,通过获取多时空、高维度的蚂蚁群集网络的随机分布,基于信号的随机轨迹机会地控制蚂蚁个体状态。获取机会蚂蚁群集网络的GPS信号频域表征后,生成GPS弱信号多频段融合体,并提出多频段融合GPS弱信号跟踪采集算法。仿真实验结果表明,该算法与静态蚂蚁群集算法相比执行时间更短,与未提取GPS弱信号的跟踪采集算法相比具有更高的跟踪精度和信号采集敏感度。

[1] 高斌斌.煤矿员工考勤与井下人员定位系统的研究[J].机械工程与自动化,2015(6):163-164.

[2] 王 汐,周少武,曾照福,等.微小型群机器人室外组合定位系统与方法[J].计算机工程与应用,2015,51(15):261-265.

[3] 邓承刚,李国徽,杨 浩,等.基于指引因子蚂蚁算法的仿真资源分配策略[J].华中科技大学学报(自然科学版),2015,43(9):1-6.

[4] GHANI H A,HAMZAH M H,SYAHALI S,et al.Ant-colony Algorithm with Interference Cancellation for Cooperative Transmission[J].IET Signal Processing,2016,10(6):603-610.

[5] 毛昱天,陈 杰,方 浩,等.连通性保持下的多机器人系统分布式群集控制[J].控制理论与应用,2014,31(10):1393-1403.

[6] 杨盼盼,刘明雍,雷小康,等.群集系统分群行为建模与控制研究进展[J].控制与决策,2016,31(2):193-206.

[7] 褚福芳,杨洪勇.具有干扰的多自主体系统的群集运动与速度同步[J].复杂系统与复杂性科学,2015,12(1):85-91.

[8] 胡 雨,谢 凯, 阮宁君,等.基于三维曲波变换的弱信号恢复方法研究[J].计算机工程与应用,2016,52(18):199-202.

[9] 芮国胜,刘林芳,张 嵩,等.变相位周期策动力杜芬振子弱信号检测方法[J].电子测量与仪器学报,2015,29(11):1662-1668.

[10] 卫 洁,范胜林,周 超,等.多径干扰下GPS弱信号跟踪算法研究[J].云南民族大学学报(自然科学版),2014,23(5):373-378.

[11] 董世明,陈一民,黄 晨,等.基于压缩感知的长时间实时跟踪技术研究[J].计算机应用与软件,2015,32(5):207-211.

[12] ZHU C,FAN X.A Novel Method To Extend Coherent Integration for Weak GPS Signal Acquisition[J].IEEE Communications Letters,2015,19(8):1343-1346.

[13] LANG R,LI X,GAO F,et al.Re-scaling and Adaptive Stochastic Resonance as a Tool for Weak GNSS Signal Acquisition[J].Systems Engineering and Electronics,2016,27(2):290-296.

[14] BRAHIM F,CHONAVEL T,TRUBUIL J,et al.Precise Acquisition of Global Navigation Satellite System Signals in the Presence of Multipath and Influence on Tracking Capability[J].IET Radar Sonar Navigation,2015,9(7):790-801.

[15] GAO Z,DAI L,WANG Z,et al.Spatially Common Sparsity Based Adaptive Channel Estimation and Feedback for FDD Massive MIMO[J].IEEE Transactions on Signal Processing,2015,63(23):1.