基于认知发育的移动机器人自主导航
2018-01-18,,,,
,,, ,
(1.北京工业大学 电子信息与控制工程学院,北京 100124; 2.防灾科技学院 防灾仪器系,河北 三河 065201; 3.计算智能与智能系统北京市重点实验室,北京 100124)
0 概述
近年来,科学技术的发展对移动机器人的自主导航技术提出越来越高的要求,自主导航成为移动机器人的基本任务,特别是当面临复杂的、动态的、非结构化环境时,需要机器人具有自主性和适应性,这依赖于机器人的认知学习能力。人和动物具有很好的环境认知能力,模拟这种认知学习机能,赋予移动式机器人类似的环境认知功能,是实现自主导航,成为真正智能系统的最佳途径[1-2]。相关的研究已有诸多文献报道:文献[3]基于强化学习提出一种移动机器人反应式导航方法,成功地应用于CIT-AVT-VI移动机器人平台;文献[4]设计了动态环境导航中的多步学习算法;文献[5]为NAO机器人在未知环境下的自主行走设计了基于KEF-SLAM的Q学习避障算法;文献[6]构建的机器人StalkerBot能预测人的行为,自主跟随导航;文献[7]研究了基于模糊逻辑和强化学习的自主导航;文献[8]提出了 Task Graph 算法,通过学习实现自主导航;文献[9]创建了条件转移图,一种能学习动态环境知识的导航策略;文献[10]模拟蟑螂的行为建立了可学习未知环境拓扑信息的模型,实现自主导航,取得了理想的效果。
虽然模拟生物的认知与行为学习对移动机器人自主导航的研究已取得了一些研究成果,但是,这些成果仅模拟了生物的认知学习特性,让机器人只是具备了一定的学习能力,实现的只是感知-动作匹配学习,缺乏解决复杂问题的能力,导致机器人在未知环境中的自主性和自适应性较差。归其原因,主要是现有的认知学习模型还不能完全反映生物神经系统的真实结构和功能,例如生物的另一重要特性——心智发育。日本大阪大学的Asada教授等人提出了认知发育机器人学的概念。认知发育机器人学中的“发育”主要指心智发育或认知发育,即机器人知识和技能的形成和发展。Asada 领导了日本的JST ERATO浅田人工合成智能工程,构造了具有仿生肌体的孩童机器人 CB2,用于认知发育机器人学的研究[11]。美国密歇根大学的翁巨扬教授提出了自主心智发育的概念[12]。基于这一理论,翁巨扬教授及其团队建造了SAIL[13]和Dav[14]2个人形机器人,相关研究工作持续至今。北京工业大学阮晓钢教授设计了一种新的斯金纳自动机,并成功应用在其团队制作的仿生两轮机器人上,机器人能够以类似人的认知和发育特性,自主地认知学习平衡控制技能[15]。但是,目前模拟生物的发育特性实现机器人自主导航的相关文献较少。
机器人本质上是一种仿生系统,应如同人和动物一样具有认知学习和发育的智能行为,其中,尤为重要的是发育特性和学习能力,以适应复杂的外界环境。因此,针对移动机器人自主导航问题,本文以神经网络为框架,基于生物学的认知和发育机理,构建一种移动机器人可计算认知发育模型,使机器人可以模拟动物从环境中自动获取知识和积累经验,通过认知发育,自组织地逐渐形成、发展和完善自主导航技能。
1 认知发育模型
认知发育模型结构如图1所示,其通过与环境的互动,形成一个闭环反馈连接。行为a(t)是认知发育模型t时刻的输出,也是认知学习的结果,行为一方面作用在环境上引起强化刺激,一方面与强化刺激共同作用,使t时刻状态s(t)转移到s(t+1)。动态发育神经网络在行为a(t)及状态s(t+1)的作用下,产生认知发育模型的能量E(t),表征认知发育系统趋向性。根据趋向性,神经网络的隐层节点会动态调整,模拟类似于生物的发育特性。在动态神经网络发育结果和强化刺激的指引下,基于认知学习机制更新行为发生概率P(t+1),学习下一个行为a(t+1)。

图1 认知发育模型结构
可以看到,图1所示的认知发育模型模拟了生物的2个特性:发育特性和认知学习特性。
1)发育特性。动态神经网络通过隐含层所含的神经元个数的调整,来模拟生物的发育特性。发育特性是心理学和热力学的混合,参考生物能量学,可以通过生物热力学来刻画。由于心理动力学和生物热力学都受到热力学的启发并与能量有关,因此可以认为在发育的过程中,心理的与生理的状态需要能量来保持,并且行为也需要能量来执行。因此,在发育过程中,将生物视为一个能量系统,其能量E(t)包括状态的能量和行为的能量,变化的能量用一个动态神经网络来逼近。同时,能量E(t)的变化,反馈回动态神经网络,构成一个反馈系统,指引动态神经网络发育的方向。
2)认知学习特性。在任意时刻,认知发育模型通过与环境的交互获得环境的强化刺激,进而获得表征认知趋向的能量变化,基于此,认知学习机制可以通过更新行为选取概率p(t)实现认知学习。下一个行为的概率由环境的强化刺激及当前行为的概率共同决定。可以看出,认知发育模型的认知学习不是盲目的,是用认知的方式来进行强化学习,强化刺激总是试图奖励好的行为并且惩罚坏的行为。
强化在形成或者改变人和动物的行为中扮演了重要的角色。如果认为强化不是正的就是负的,那么可以将奖励和惩罚看作是强化,其中正的强化刺激代表奖励,负的代表惩罚[15]。
2 学习算法设计
2.1 认知学习算法
按照生物的认知发育特性,机器人的认知发育系统可以视为一个能量系统,总能量为E(t),包括状态能量函数Es(t)和行为能量函数Ea(t),其中,Es(t)表示状态的非负能量值,Ea(t)表示行为的非负能量值。总能量表达式如下:
E(t)=ΔEs(t)+Ea(t)
(1)
其中,ΔEs(t)=Es(t+1)-Es(t)是状态能量从t到(t+1)时刻的增量,表征状态能量的变化,其变化由行为能量Ea(t)所致,而状态能量的变化表示状态发生了转移。
2.1.1 行为概率的更新
假设低能量的状态与生物的趋向性一致,则在生物的认知发育过程中,趋向性的含义就是通过低能量的行为来保持低能量的状态。因此,可以将能量变换变化的趋向性作为发育和认知学习的强化刺激,其计算形式如下:

(2)
其中,p(a(t)|s(t))是行为a(t)在状态s(t)下的发生概率,Δp(a(t)|s(t))是发生概率p(a(t)|s(t))的增量。
文献[16]提出了用于全局优化的模拟退火算法。模拟退火算法定义如下:模拟退火其实是一种贪心算法,在搜索过程中,引入了随机因素,以一定的概率来接受一个比当前解要差的解,因此,有可能会跳出这个局部的最后解,达到全局的最优解。按照该定义,显然模拟退火算法和认知学习过程具有相似的特性,模拟退火算法中的降温可看作认知学习过程中的强化。本文结合蒙特卡洛算法[17]和模拟退火算法来设计认知学习算法。
在认知发育过程中,状态s(t+1)为行为a(t)执行的结果,如果状态s(t+1)的能量比状态s(t)的能量高,则调节行为a(t)在状态s(t)下出现的概率,使s(t+1)出现在s(t)之后的机会概率减小,反之依然。因此,行为a(t)在状态s(t)下出现的概率设计如式(3)所示。
(3)
其中:E(a|s)=ΔES(a|s)+EA(a|s)为认知发育系统的能量,A为行为集合,S为状态集合,EA(a|s)是行为a∈A在状态s∈S下的行为能量,ΔES(a|s)是在行为a∈A的作用下引起的状态能量增量;〈·〉为在认知学习过程中,行为a在状态s下反复出现时的系统能量统计量;T是温度;KB是玻尔兹曼常数;R(t)为强化刺激信号。把强化刺激信号R(t)加入到概率更新公式中,一方面,结合温度变化,引导概率改变的方向,使机器人更倾向于选取对自己有利的行为;另一方面,能使设计的认知发育学习模型体现出更类似于动物的取向特性。
2.1.2 行为熵
熵的概念是从热力学第二定律得出,被推广为系统无序度的量度。在信息论中,熵可用作某事件不确定度的量度。信息量越大,体系结构越规则,功能越完善,熵就越小。利用熵的概念,可以从理论上研究信息的计量、传递、变换、存储[18]。本文引入行为熵的概念来描述认知发育模型中行为的不确定性。

(4)
此处利用行为熵用来表征机器人行为的不确定性。由熵的定义可以推理出,当温度降低时,认知发育模型的熵随之降低,并逐渐收敛为0。这说明在认知发育模型中,认知学习的过程是一个自治的过程。
2.2 动态发育算法
神经网络学习的过程模仿了高等生物探索、调节、总结的学习规律,其映射关系具有高度的非线性和不确定性。而动态神经网络的结构可以根据学习的经验动态调整,与生物的发育特性很相似。本文设计了一种动态结构神经网络,产生机器人总能量E(t),结合热力学过程来模拟生物的发育特性。该网络在发育过程中可以动态地插入和删除神经元节点,最终得到与应用需求相匹配的网络规模。
动态结构神经网络为一个三层感知器网络,包括输入层、输出层和隐层,输入层和输出层根据实际问题确定其各自的维度,假设网络的输入是n维向量,用S={s1,s2,…,sn}表示,此处选取机器人的状态信息作为输入;输出是n×r维向量,用E={E1,E2,…,En×r}表示,此处选取认知发育系统的能量E(a|s)作为输出;隐层个数以及每个隐层所包的神经元个数在训练过程中进行动态调整,包括在邻接输出层的隐层插入新的神经元节点或者创建新的隐层。初始隐层只有一个神经元,如图2所示。
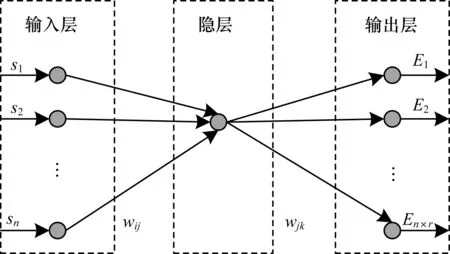
图2 网络初始化结构
隐层神经元的激发函数采用双极性sigmoid函数:
(5)
为了增加动作选择的区分度,输出层采用线性函数:

(6)
其中,w、N、p均为正实数,可根据情况设定。用Net(l,n)表示神经网络的结构,l为神经网络隐层数,n为隐层神经元的个数。
当前时刻t网络Net(l,n)的训练误差表示为式(7)。
(7)
其中:ΔE(a,s)表示认知发育系统能量的变化量;τ是一个很大的正整数,表明网络会滚动计算误差,进行训练调整;r表示输出层神经元个数。在训练过程中,通过认知发育,动态调整隐含层l的值和每个隐含层所含的神经元n的值,其他层神经元的个数不发生变化,
若当前神经网络结构的训练误差ε(l,n)满足式(8),在隐层中插入神经元节点(如图3所示),则隐层的神经元个数由n变为n+1。
(8)
其中:ε0表示误差水平;ξ为一小正数,表征误差变化的程度;q为一小正整数。新神经元与邻层神经元产生的权值初始化为随机数:
ωij=random(-0.5,0.5)
(9)

图3 新节点插入过程
若在同一隐层内连续插入q个神经元仍不能使误差显著减小,如式(10)所示,向网络中插入新的隐层及对应的神经元(如图4所示),则网络的隐层数由l变为l+1。
(10)
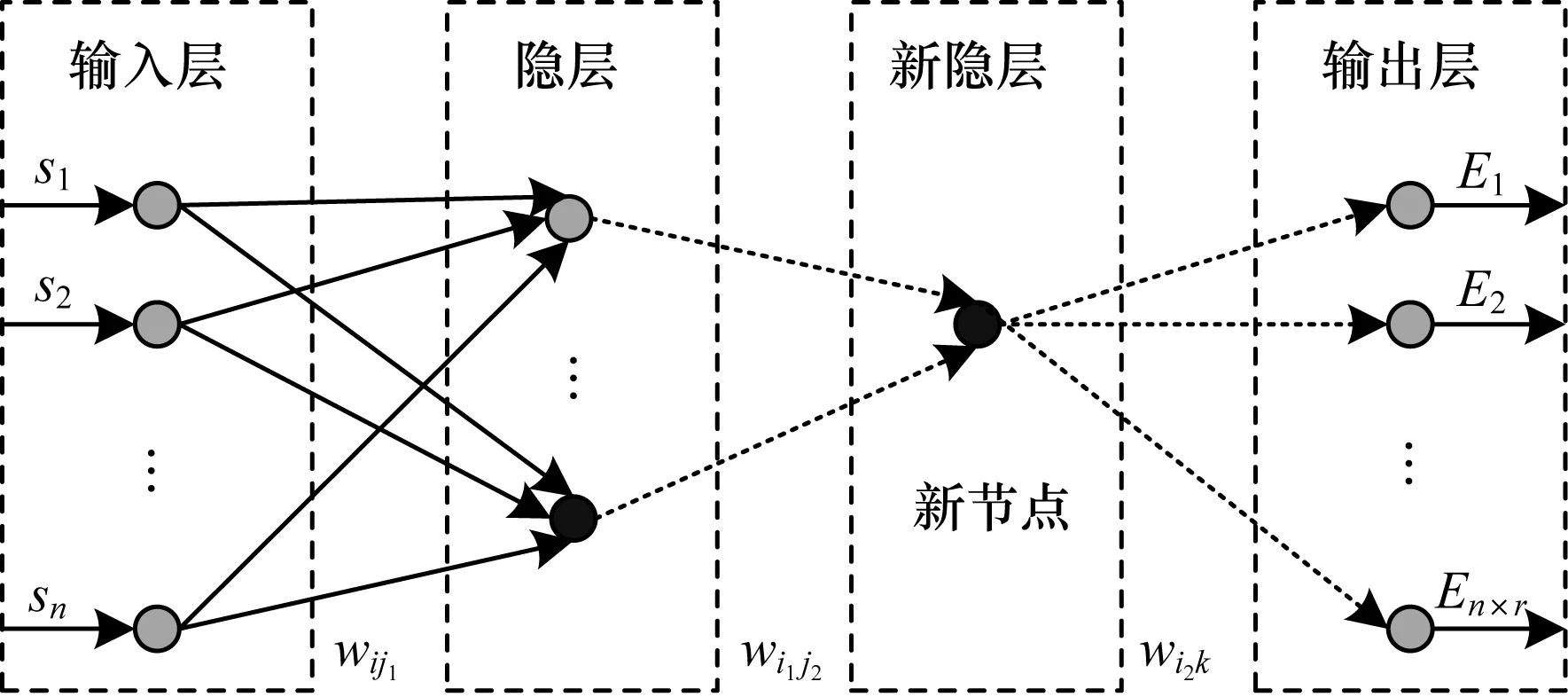
图4 新隐层插入过程
新插入的神经元节点和相邻的神经元均为全连接,权值同样按式(9)的方式初始化。神经网络的结构每变化一次,都要进行足够次数的训练,直至网络的误差变化不再明显。
2.3 学习算法收敛性分析
定理当t→时,认知发育学习模型的行为熵H(t)收敛至极小,即:式中Hmin为小常数。
证明:
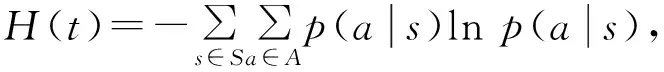
2)当t→时,任意状态的行为熵为:
(11)
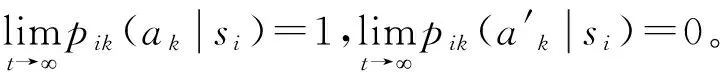
(12)
证毕。
上述定理表明,随着时间的延长,温度逐渐降低,行为熵不断减小,直至收敛至极小值,直至最终温度。这也说明,认知发育学习是一个自治的过程。
3 移动机器人学习导航
3.1 机器人学习导航原理
机器人配备检测装置,获取机器人导航所需要的信息。机器人与工作环境关系示意如图5所示。

图5 机器人和障碍物及目标点间关系
机器人状态包括:机器人位于障碍物左方、前方和右方3个方向的距离信息;机器人与目标点的距离信息及与目标点间的夹角。因此,参看文献[19]机器人的状态空间定义如下:
定义1机器人的状态空间s为:
s={dr_l,dr_f,dr_r,dr_tar,θ}
(13)
其中,dr_l为机器人左侧距障碍物的距离,dr_f为机器人前方距障碍物的距离,dr_r为机器人右侧距障碍物的距离,dr_tar为机器人与目标点之间的距离,θ为机器人运动方向和目标点的夹角。
满足下式:
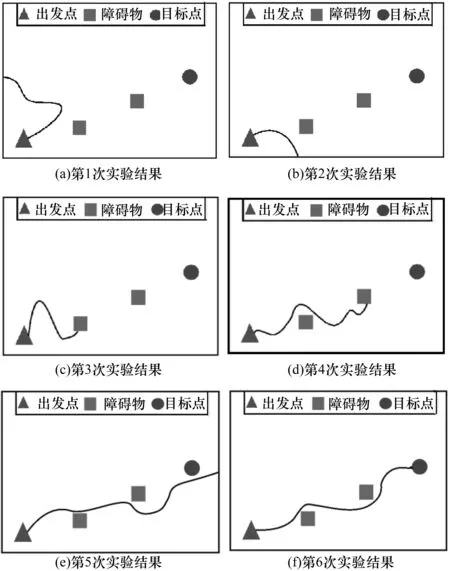
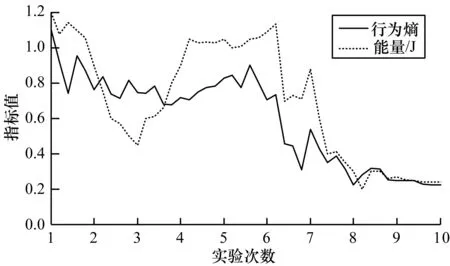
dmin≤min(dr_l,dr_f,dr_r) 其中,dmin表示最小危险距离,当任一探测距离小于dmin时表示移动机器人避障失败,dmax表示最大安全距离,当各方向探测距离均大于dmax时机器人可以以最大速度安全行走。 本文将机器人的行为分解为5个,行为空间定义如下: 定义2机器人的行为空间A为: A={a1,a2,a3,a4,a5} 其中,a1表示机器人转动+20°同时向前移动0.1 m,a2表示机器人转动-20°同时向前移动0.1 m,a3表示机器人转动+10°同时向前移动0.1 m,a4表示机器人转动-10°同时向前移动0.1 m,a5表示机器人向前移动0.1 m。 1)机器人和目标点的距离缩小,表现为: (14) 2)机器人和障碍物之间的距离扩大,表现为: (15) 3)机器人朝着目标点运动,表现为: (16) 机器人的强化信号定义为: R(t)=-αRr_tar(t)+βRr(t)-ηRθ(t) (17) 其中,0<α,β,η<1。 因此,机器人的状态能量函数定义如下: Es(t)=R2(t)+ρRr_tar·Rr(t)·Rθ(t) (18) 其中,R2(t)代表了机器人对朝着目标点方向、避开障碍物、离目标越来越近的3个趋向,ρRr_tar·Rr(t)·Rθ(t)是考虑3个趋向之间的耦合,ρ为耦合系数,满足0<ρ<1。 机器人以认知发育的方式完成未知环境下避障导航,具体过程如下: 1)机器人依据检测装置获取环境信息,包括机器人和目标点之间的距离、夹角、机器人周围的障碍物距离等,将其作为认知发育模型的状态,输入到动态神经网络中。 2)计算动态神经网络的输出,得到认知发育模型的能量及能量变化情况,获得认知发育系统发育和认知学习的趋向。 3)根据动态神经网络的发育和认知学习的趋向,更新行为概率,并按照概率从行为空间选择一个行为。 4)执行选中的行为,改变环境状态。 5)获得强化刺激信号,训练动态神经网络。当满足停止条件时,退出学习过程,否则进入下一轮学习。 机器人通过检测装置检测环境获取信息,之后根据行为概率从行为空间选择一个“合理”的行为执行。随后,根据行为执行前后环境反馈的强化刺激训练动态神经网络。按照这样的顺序循环执行,直到网络训练完成,然后将神经网络的权值和结构固化,退出学习过程。 机器人通过检测装置检测环境获取信息,之后根据行为概率从行为空间选择一个“合理”的行为执行。随后,根据行为执行前后环境反馈的强化刺激训练动态神经网络。按照这样的顺序循环执行,直到网络训练完成,然后将神经网络的权值和结构固化,退出学习过程。 物理实验采用的是一款简易仿生机器鱼,如图6所示,该机器人是一款简易移动机器人,适合于水中环境下的导航实验。机器人通过外置摄像头感知环境,摄像头摄像范围必须能覆盖到整个场地,因此,设置了2个位于导航环境中心的摄像头,摄像头为大恒水星系列MER-040-60UC型号(如图7所示),可以完成视觉定位,通过在场地建立的坐标系推算出仿生鱼实时的位置。 图6 仿生机器鱼示意图图7 摄像头示意图 图8 实验环境俯视图 图9 实验环境 在物理实验中,基于采集到的机器鱼导航过程中的实际数据绘制其导航轨迹,如图10所示。 图10 机器鱼导航轨迹 实验结果发现,经过5次学习之后,机器鱼经过发育和学习,已习得自主导航技能,能自主地从出发点无障碍的巡航至目的地。从第6次实验开始,机器人能准确的前往目的地,巡航路径变得稳定。对机器人避障导航过程进行了视频录制,图11展示了某次成功实验的部分截图。 图11 机器人避障导航过程 为了进一步验证本文设计方案的有效性,绘制了人工势场方法导航轨迹,如图12所示,与图10(f)相比可以看出,与模拟仿真结果类似,基于人工势场法的轨迹不平滑,路径并非最优。 图12 人工势场法实验结果 更改出发点和障碍物位置,变换实验环境如图13所示,重复以上实验,为了测试机器人的认知能力,障碍物个数增加,变得更复杂,使得机器鱼的可行路径更狭窄,增加环境复杂度。实验结果如图14所示,从实验结果中可以看到,机器人仍然能够实现从起点开始穿越障碍抵达终点的自主巡航。这说明设计的自主认知发育模型对于机器人的自主认知导航具有一定的泛化能力,即使环境信息有所变化,机器人也能很快地适应,重新发现规律。对机器人避障导航过程进行了视频录制,图15展示了某次成功实验的部分截图。 图13 改变后的实验环境 图14 改变环境后的导航轨迹 图15 改变环境后的机器人避障导航过程 上述实验结果表明,机器人在巡航过程中,每到一处位置便通过传感器获得与障碍物、目的地的距离信息,然后经过认知发育模型处理之后,转换成对应的行为选择,实现从感知到运动的映射转换。如果行为选择有利于避开障碍、靠近目的地,则通过调整网络权值,降低系统能量,行为选择的几率增大;反之,则系统能量增大,行为选择的概率变小。同时,机器人将这些习得经验以增加神经网络隐层节点的方式,记忆在网络中。机器人在整个过程中没有监督信号的指引,自主的完成对环境的认知,习得最优行为。因此,机器人的自主认知巡航过程也是一个自学习、自组织和渐近发育的过程。机器人某状态下行为熵和能量的变化证明了机器人自学习、自组织的过程,如图16所示。随着学习的进行,内能均值随着温度降低也越来越低,同时它的行为熵也在不断减小,直至最终收敛至最小值。行为熵和内能的不断减小反映了自组织程度的不断提升。同时,也说明机器人的认知发育学习是自治的。 图16 行为熵和能量的变化曲线 本文构建一种模拟生物学认知和发育机理的认知发育模型,以实现机器人的自主导航。根据应用环境的需要,神经网络的结构可以实现动态调整和自组织,类似生物的发育过程,网络的复杂程度和环境保持匹配,确保神经网络可解决应用问题同时保持紧凑结构。认知发育算法用Metropolis Monte Carlo方法和模拟退火的方式模拟认知学习以及行为选择过程,使得机器人可以像热力学系统一样运行。对机器鱼的多种导航任务进行了实验分析,结果证明,机器人可以模拟动物从环境中自动获取知识、积累经验,通过保持和环境的互动以及重复的学习和训练,达到预期的导航目标。本文主要目的是寻求一种可行性的自主导航方法,最优性退居次要位置,但在实验中发现,机器人运行的轨迹有些抖动,并未实现严格意义上的路径最优,因此,寻求最优性将是下一步的研究方向。 [1] LAKE B M,SALAKHUTDINOW R,TENENNBAUM J B.Human-level Concept Learning Through Probabilistic Program Induction[J].Science,2015,350(6266):1332-1338. [2] 王子强,武继刚.基于学习算法的移动机器人路径规划[J].计算机工程,2014,40(6):211-214. [3] 徐 昕.增强学习与近似动态规划[M].1版.北京:科学出版社,2010. [4] YU C,WANG C C.Multi-step Learning to Search for Dynamic Environment Navigation[J].Journal of Information Science and Engineering,2014,30(3):637-652. [5] WEN Shuhuan,CHEN Xiao,MA Chunli.The Q-learning Obstacle Avoidance Algorithm Based on EKF-SLAM for NAO Autonomous Walking Under Unknown Environments[J].Robotics and Autonomous Systems,2015,72(C):29-36. [6] MURPHY L,CORKE P.STALKERBOT:Learning to Navigate Dynamic Human Environments by Following People[C]//Proceedings of Australasian Conference on Robotics and Automation.Wellington,New Zealand:Australasian Robotics and Automation Association,2012:1-9. [7] CHERROUN L,BOUMEHRAZ M.Fuzzy Logic and Reinforcement Learning Based Approaches for Mobile Robot Navigation in Unknown Environment [J].Journal of Measurement and Control,2013,9(3):109-117. [8] KOREIN M.Scheduling Mobile Exploration Tasks for Environment Learning[C]//Proceedings of the 12th International Conference on Autonomous Agents and Multiagent Systems.Saint Paul,USA:International Foundation for Autonomous Agents and United States,2013:1-2. [9] KUCNER T,SAARINEN J,MAGNUSSON M,et al.Conditional Transition Maps:Learning Motion Patterns in Dynamic Environments[C]//Proceedings of IEEE International Conference on Intelligent Robots and Systems.Tokyo,Japan:Institute of Electrical and Electronics Engineers Inc.,2013:1196-1201. [10] DIRAFZOON A,LOBATON E.Topological Mapping of Unknown Environments Using an Unlocalized Robotic Swarm[C]//Proceedings of IEEE International Conference on Intelligent Robots and Systems.Washington D.C.,USA:IEEE Press,2013:5545-5551. [11] ASADA M,HOSODA K,KUNIYOSHI Y,et al.Cognitive Developmental Robotics:A Survey[J].IEEE Transactions on Autonomous Mental Development,2009,1(1):12-34. [12] WENG J,MCCLELLAND J,PENTLAND A,et al.Artificial Intelligence:Autonomous Mental Development by Robots and Animals[J].Science,2001,291(5504):599-600. [13] ZHANG Yilu,WENG Juyang,HWANG W S.Auditory Learning:A Developmental Method[J].IEEE Transactions on Neural Networks,2005,16(3):601-616. [14] WENG J.Teachable Robots[J].Technology Review,2008,106:64-67. [15] RUAN Xiaogang,WU Xuan.The Skinner Automaton:A Psychological Model Formalizing the Theory of Operant Conditioning[J].Science China Technological Sciences,2013,56(11):2745-2761. [16] KIRKPATRICK S,GELATT C D,VECCHI M P.Optimization by Simulated Annealing[J].Science,1983,220:671-680. [17] NICHOLLS D G,FERGUSON S J.Bioenergetics[M].[S.l.]:Academic Press,2013. [18] 阮晓钢.神经计算科学:在细胞的水平上模拟脑功能(人工智能之路)[M].北京:国防工业出版社,2006. [19] 乔俊飞,樊瑞元,韩红桂,等.机机器人动态神经网络导航算法的研究和实现[J].控制理论与应用,2010,27(1):111-115.3.2 物理实验与分析









4 结束语
