不同植筋方案纵连板轨道砂浆层抗剪性能分析

钟阳龙， 高 亮， 侯博文

(1.北京交通大学土木建筑工程学院，北京100044;2.轨道工程北京市重点实验室，北京100044)

无砟轨道是高速铁路的主要轨道形式，由于具有平顺性高、稳定性好、维修量少和社会经济效益显著等优点［1-2］而被广泛应用.其中 CRTSⅡ型纵连板式轨道是中国无砟轨道典型结构形式之一，已先后应用于京津、沪杭、京沪、沪昆等线路上，运营总里程约 5 000 km［3］.

目前CRTSⅡ型板式无砟轨道总体使用情况良好，但由于受复杂环境条件影响(如华东地区夏季持续高温)，个别薄弱区段出现了轨道板上拱离缝、宽接缝破损等病害［4］.病害的产生破坏了纵连板式轨道的整体性［5］，在较大温度力作用下可能导致轨道层间剪切破坏而形成大范围的离缝，并产生较大的纵向位移，对轨道结构的稳定性产生极为不利的影响.为控制轨道板位移，在整治以上病害时一般首先采用植筋方法对轨道板进行锚固.针对轨道板的植筋锚固方案，国内部分学者已开展相关研究:苗雨［6］基于力的平衡，采用轨道板温度力减砂浆黏结力再除以单根剪力筋抗剪设计值的计算方法得到了植筋总数，该方法计算简便，但对轨道结构受力简化较多;针对以上不足，任娟娟等［7］采用有限元法建立了Ⅱ型板式无砟轨道三重叠合梁模型，并考虑CA砂浆与轨道板相互作用力随相对位移的增大而增大，且增大到一定值后保持不变的非线性特性，计算了不同植筋量轨道板在整体升温下的纵向位移，并对不同植筋方案的限位能力进行了对比分析;谭社会［3］采用同样的CA砂浆与轨道板相互作用关系，建立无砟轨道空间耦合实体模型，分析了植筋锚固对轨道板离缝上拱的整治效果.

王继军、孙立、刘钰、戴公连等［8-11］曾开展了轨道层间抗剪性能的推板试验研究，结果表明，在推力作用下轨道层间表现出黏结-脱黏-接触的剪切破坏过程，轨道层间剪切破坏后，层间黏结力严重衰减，将无法继续抵抗剪切荷载的作用.可见既有文献在开展轨道植筋方案研究时虽然考虑了CA砂浆对轨道板的非线性约束作用，但并未考虑层间剪切破坏后CA砂浆黏结力的衰减.针对此不足，本文采用基于表面的内聚力模型［12］(SCZM，surface based cohesive zone model)模拟轨道层间黏结-脱粘-接触的复杂相互作用关系，对不同植筋方案下轨道砂浆层间抗剪性能进行分析，并研究提出不同升温幅度下的植筋方案，为纵连板式轨道养护维修提供参考.

1 轨道层间抗剪性能分析模型

1.1 基于表面的内聚力模型

通过定义两黏结面之间的牵引力(t)-相对位移(δ)非线性本构关系(图1)，并依据强度准则判定伤损萌生，基于断裂力学分析裂纹扩展，采用接触属性定义界面接触摩擦，巧妙地实现了界面裂纹萌生-界面断裂-摩擦接触过程的模拟.目前，基于表面的内聚力模型已被广泛应用于纤维增强复合材料［13］、编织复合材料［14］、耐火材料、水库大坝等的界面裂纹扩展分析.

图 1 中:δm，f为层间脱粘时的相对位移;δm，0为层间损伤萌生时的相对位移.

图1 基于表面的内聚力模型牵引力-相对位移关系Fig.1 Traction-separation behavior of SCZM

本文采用的牵引力-相对位移关系(如图1)可描述如下:

(1)初始阶段，牵引力随着相对位移增大而线性增大，表现为线弹性属性，此时层间应力较小，无伤损产生;

(2)当牵引力达到临界值tult时，伤损萌生，伤损萌生判定条件为二次名义应力准则［15］(quadratic nominal stress criterion)为

式中:

tn、ts、tt分别为法向、第一切向、第二切向的牵引力;

t0，n、t0，s、t0，t分别为法向、第一切向、第二切向的抗剪强度;

??表示在纯压缩位移或纯压缩应力状态下不会发生损伤.

(3)伤损产生后，界面刚度随着相对位移的增加而减小，伤损程度逐渐增加.

引入标量D来定量评估损伤程度，称为损伤因子［14］.损伤因子定义为

式中:

δm，max为整个分析过程中的有效相对位移.

D取值范围为0～1:当D=0时，表明没有伤损;当D=1时，表明完全伤损，层间脱粘.伤损产生后，牵引力-相对位移关系可描述为［13］

式中:

kn、ks、kt分别为法向、第一切向、第二切向各个方向的刚度系数;

δn、δs、δt分别为为法向、第一切向、第二切向的相对位移.

伤损演化过程伴随着能量的释放，因此可以基于断裂能来定义伤损演化后层间脱粘的判定条件.断裂能数值上等于牵引力-相对位移曲线下所围成的面积.当界面断裂能达到断裂韧度限值时，层间开裂.断裂准则为［13］

式中:

Gn为法向的界面能量释放率;

Gs为第一切向的界面能量释放率;Gt为第二切向的界面能量释放率;GC，n、GC，s、GC，t分别为不同断裂模式下的界面断裂韧度.

当界面能量释放率满足式(4)时，界面黏结失效.当界面失效后，层间通过接触作用，接触面之间包括法向作用和切向作用:法向作用描述为接触压力与压缩量的关系，本文采用“硬接触”模拟［16］;切向作用定义为库伦摩擦.

1.2 无砟轨道有限元模型建立

由于本文主要关注温度力作用下轨道层间剪切作用，不考虑下部基础的影响，为简化结构分析，模型中仅考虑轨道结构部分.另外，由于无砟轨道结构损坏修复作业中一般会松开部分扣件，因此偏安全设计考虑，忽略钢轨的限位作用，模型中不考虑钢轨和扣件［17］.因此，模型主要由轨道板、CA砂浆和底座板组成.

现场调研表明，层间离缝主要发生在轨道板与砂浆层之间［18］，砂浆层与底座板可看作完全相互黏结.因此，本文在轨道板与砂浆层之间建立基于表面的内聚力界面属性，砂浆层与底座板之间共用节点.考虑不同植筋方案下模型长度需求以及边界影响，通过试算选取模型长度为65 m.将模型一端所有结构的纵向自由度约束，而另一端仅约束CA砂浆和底座板的纵向自由度，以此来模拟轨道板在此处被解锁，另外，完全约束底座板底部节点自由度.计算中考虑温度和重力荷载的耦合作用，同时加载于整个模型上.轨道板、砂浆层与底座板都采用8节点实体单元模拟.为保证计算精度和内聚区内单元个数要求［19］同时借鉴文献［18］的网格大小，通过对比 0.10、0.05 m 和 0.02 m 3 种网格的计算结果后，确定本文模型网格单元尺寸为0.1 m.

单块板上的剪力筋布置形式主要有8、10、16根3种.每种形式下都是每排植2根剪力筋，则分别对应植4、5、8排.剪力筋布置需要均匀对称，具体的布置图可参见文献［7］.剪力筋刚度试验［16］表明，剪力筋受力变形存在明显的非线性.试验得到单根剪力筋最大剪切承载力为60 kN，错动位移为0.6 mm，可得到剪力-位移关系如图2所示.

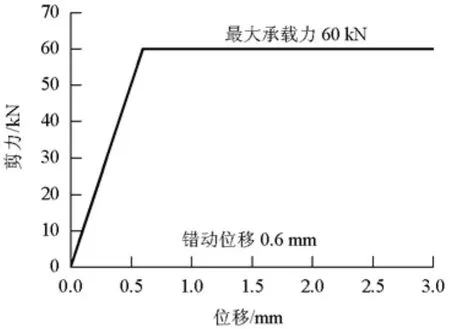
图2 剪力筋剪力-位移本构关系Fig.2 Force-displacement constitutive of shearing steel bar

采用非线性弹簧单元模拟剪力筋，通过列表输入试验所得的力-位移关系曲线，赋予弹簧单元非线性属性.轨道主要参数见表1、2.基于以上建模方法，采用有限元软件ABAQUS建立的无砟轨道模型如图3所示.

1.3 模型验证

为研究CA砂浆层与轨道板界面的剪切黏结状态，国内外开展了一系列实尺模型的推板试验［9-11］，其中德国博格公司的试验结果较为典型而被广泛应用于Ⅱ型板式轨道的设计与研究中［10，17］.本文将与博格公司试验结果进行对比以验证模型.推板试验模型与1.2节所述模型类似，除模型长度取为一个板长以及模型两侧不约束，改为一侧施加位移荷载，且不考虑植筋外，其他完全相同.计算得到纵向位移-推力曲线如图4所示.

表1 轨道参数取值Tab.1 Track parameters

表2 轨道板-CA砂浆层界面参数Tab.2 Interface parameters of track slab-CA mortar layer

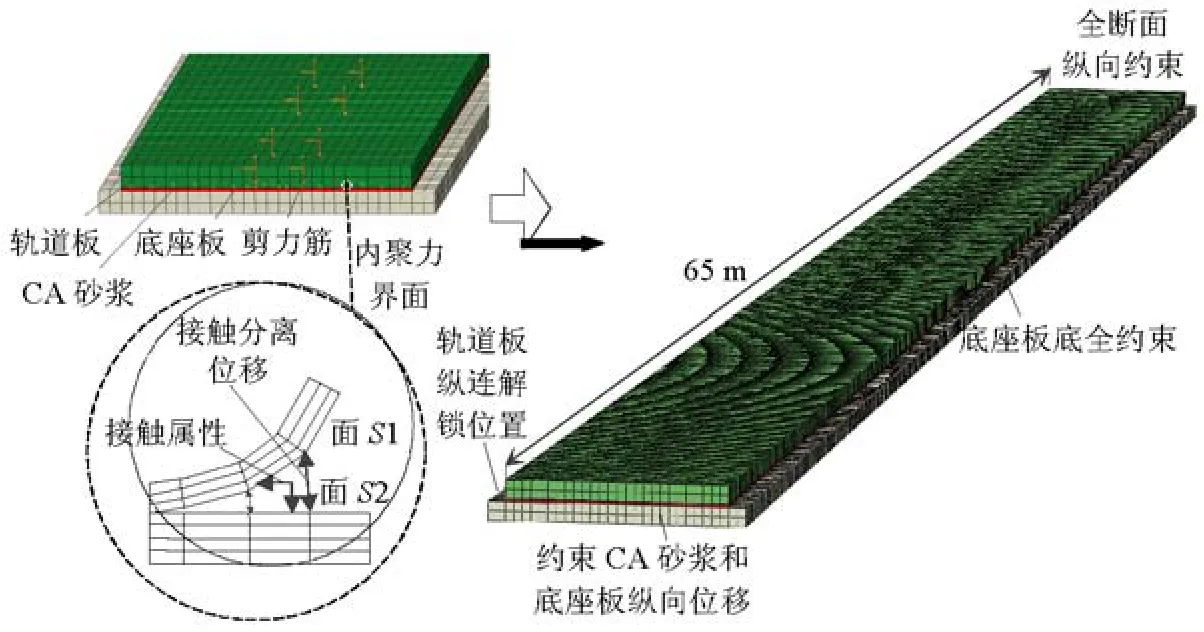
图3 无砟轨道有限元模型Fig.3 Finite element model of slab track

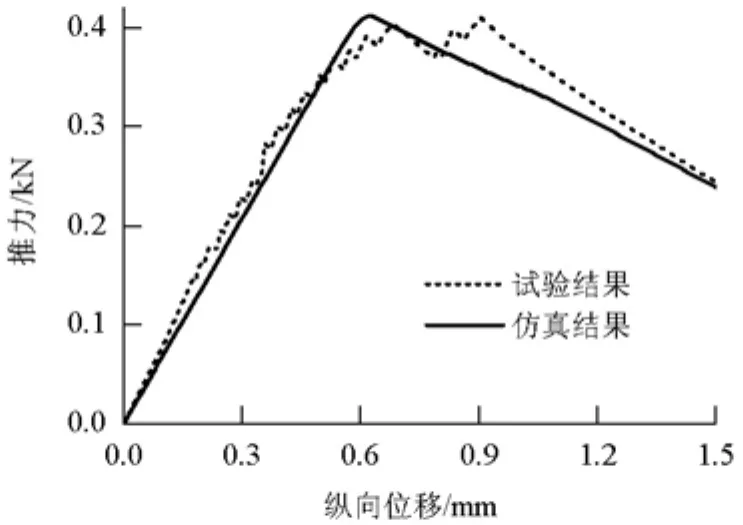
图4 推板试验结果对比Fig.4 Comparison of longitudinal shear test results

由图4可以看出，两者在整体趋势上保持较好的一致性，计算所得最大剪切荷载(412 kN)，与博格公司推板试验结果(410 kN)［10］基本相同.由此可以得出，本文所建立的层间剪切性能分析模型与试验结果吻合度较高，表明模型合理可信.

2 层间剪切破坏过程分析及植筋方案比选

首先对轨道层间剪切破坏过程进行分析，并对比有无植筋的影响，分析结果可为下一步植筋方案的确定奠定基础.

2.1 层间剪切破坏过程

本文主要考虑整体升温的作用，计算不同升温幅度下轨道板纵向位移、层间剪切应力、内聚力表面损伤变量CSDMG(damage variable for cohesive surfaces)(取值0～1，意义与1.1节中的损伤因子相同)等.

图5为4个不同升温幅度下的轨道板与CA砂浆层层间剪应力分布图.

图5实线是无植筋轨道板的剪应力分布图，虚线为前3个板植筋16+16+10的剪应力分布图，本文中植筋组合用A+B+C+…的方式表述，A为自解锁位置起第1块板的植筋量，B为第2块板的植筋量，C为第3块板的植筋量，以此类推.

由图5可知:升温1℃时，层间剪应力较小且未达到抗剪强度，剪应力分布表现为解锁处(自由端)最大，往里迅速减小;当升温5℃时，无植筋轨道自由端剪应力已超过剪切强度而导致层间微裂纹的萌生，自由端剪应力也随之减小，而植筋轨道的自由端剪应力仍未超过层间抗剪强度，说明剪力筋发挥作用，承担了一部分剪切力;当温度幅度增加到10℃时，无植筋轨道自由端的剪应力几乎衰减为0，而植筋轨道自由端剪应力刚开始减小，层间裂纹也开始萌生;当升温15℃时，无植筋轨道层间开裂，且离缝迅速扩展，层间主要依靠微弱的摩擦力作用，结构纵向失稳.

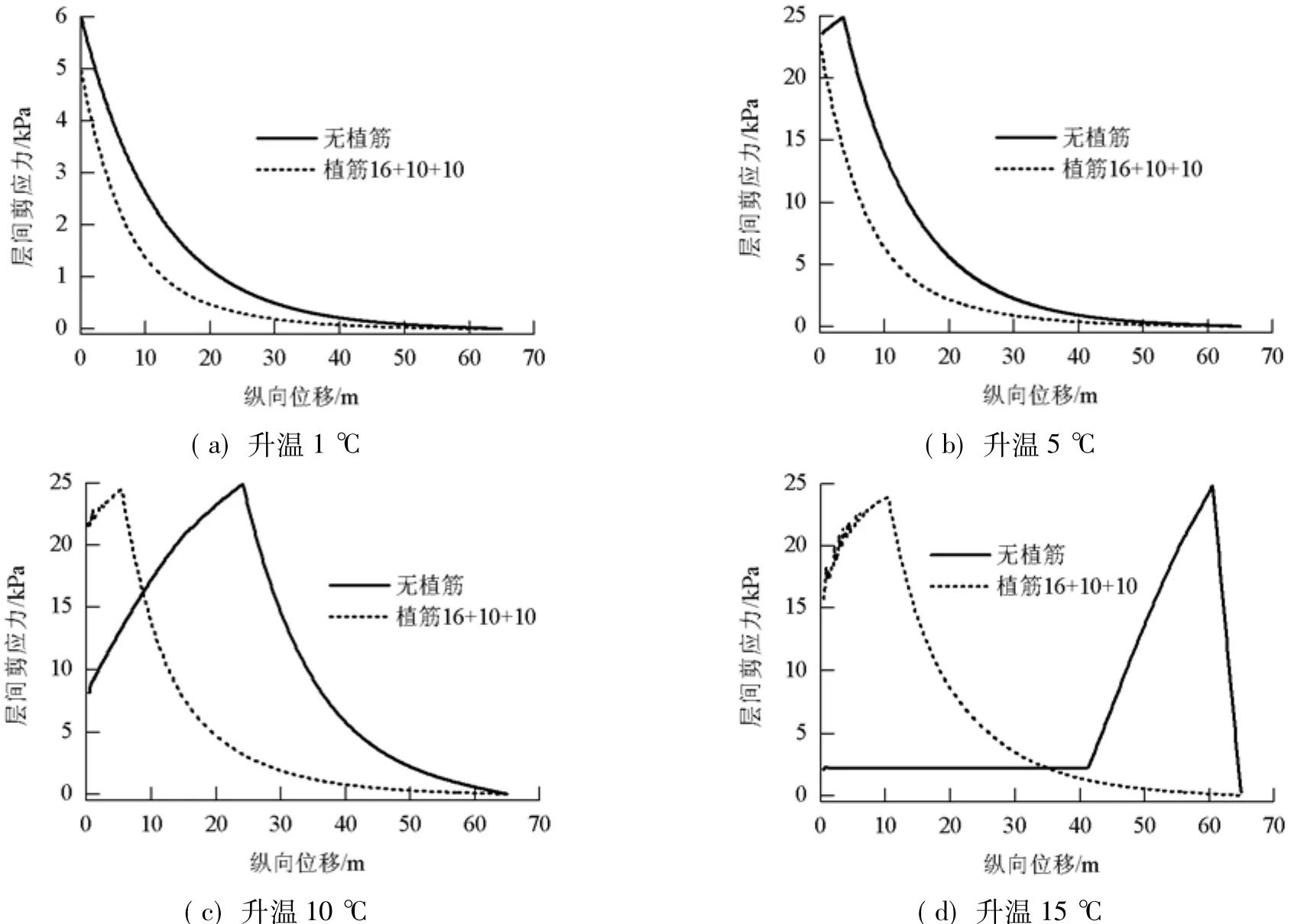
图5 升温下层间黏结剪切破坏过程Fig.5 Shear failure process of track interface under temperature load

植筋轨道虽然板端剪应力衰减明显，层间裂纹也进一步扩展，但层间并未开裂，轨道依然保持稳定.

通过以上分析可知，层间剪切破坏过程表现为弹性变形-层间裂纹萌生-裂纹扩展-层间开裂4个阶段.植筋可改善轨道层间受力，且明显提高层间抗剪能力.

为进一步分析植筋对层间裂纹萌生和层间开裂的影响，提取轨道自由端端部以及距离端部2、6、10 m等位置处不同升温幅度下的内聚力表面损伤变量CSDMG，如图6.

由图6可知:植筋后轨道层间裂纹萌生和层间开裂时的升温幅度都有所提高，尤其是层间开裂时的升温幅度变化尤为明显;以端部为例，层间开裂时升温幅度由无植筋时的10.5℃提高到了22.1℃，提高幅度达110.5%;距离自由端位置越远，层间裂纹萌生和开裂时的升温幅度也越大，而有无植筋之间的差异也越明显.说明植筋可有效控制层间裂纹扩展.

图7为轨道板纵向位移随温度的变化曲线.

由图7可知:无植筋情况下，在升温幅度小于10.5℃时，轨道板纵向位移变化非常缓慢;当升温幅度达到10.5℃时，层间离缝产生，轨道板纵向位移迅速增大，轨道纵向失稳;当轨道板纵向失稳后，轨道板最大纵向位移与伸缩长度(本文中为模型长度)密切相关，实际Ⅱ型板式轨道为全线纵连结构，伸缩长度长，轨道失稳将带来非常大的轨道板纵向位移;有植筋情况下，在升温幅度小于22.1℃时，轨道板纵向位移变化很小，表明在以上温度范围内，16+16+10的植筋方案可以有效地限制轨道板位移;当升温大于22.1℃时，轨道同样会由于层间剪切破坏而失稳，说明不同植筋方案有不同的适用范围，有必要针对不同的升温幅度提出合适的植筋方案.

图6 不同位置内聚力表面损伤变量CSDMG变化曲线Fig.6 CSDMG-temperature curves at different positions

图7 轨道板纵向位移随温度变化曲线Fig.7 Slab longitudinal displacement-temperature curve

2.2 植筋方案对比分析

本文以单块板上3种植筋锚固方式［7］为基础，组合出13种不同植筋方案，如表3所示.

图8分别为不同植筋方案下轨道自由端端部和距离端部10 m处的CSDMG指标随温度的变化情况.由图8可以看出:随着植筋量的提高，层间裂纹萌生和层间开裂时的升温幅度都有所增加，而且距离端部10 m处的增加幅度明显大于端部;在端部位置处，从植筋方案4开始，再增加植筋量对层间裂纹萌生及层间开裂的影响变得很小;在距离端部10 m位置处，从植筋方案7开始对层间裂纹萌生的影响变得很小，而从方案11开始对层间开裂的影响也变得很小.这说明植筋量达到一定程度后再增加植筋对轨道板限位能力的提高不再明显.

表3 初步设计的植筋方案Tab.3 Preliminary designed arrangement schemes of embedded steel bars 根

通过上文层间剪切破坏过程分析可知:轨道层间剪应力在自由端最大，往里逐渐衰减.剪力筋也同样表现出在端部位置剪力较大，往里越小.由此说明实际上并不是所有剪力筋都能同时起作用，这也是为何增加植筋量后限位能力未能明显提高的原因.植筋量有合理的限值，没有必要过度增加植筋量.另外，避免高温时解锁轨道以及辅助增加其他限位措施，如注胶，也很有必要.

图8 不同植筋方案下CSDMG随温度变化曲线Fig.8 CSDMG-temperature curve under different arrangement schemes of embedded steel bars

图9 为不同植筋方案下轨道板的纵向位移随温度变化曲线.

由图9可知:在升温幅度小于13℃时，各植筋方案都能较好地限制轨道板位移;升温幅度超过13℃后，植筋方案1下轨道板纵向位移迅速增大，轨道纵向失稳，随着植筋量的增加，轨道失稳时的升温幅度有所增加;当升温幅度超过30℃后，植筋对轨道纵向移动的限制效果已不明显.因此，建议升温幅度超过30℃时，需结合其他措施进行限位.

图10为升温5～45℃时不同植筋方案轨道板最大纵向位移图.

由图10可知，同一升温条件下，随着植筋数量的增多，轨道板纵向位移值减小，且减小到一定程度后趋于平稳.故某一升温幅度下存在一个最佳植筋方案，使得植筋数量不多且层间相对位移较小.

图9 不同植筋方案下轨道板纵向位移随温度变化Fig.9 Slab longitudinal displacement-temperature curve under different arrangement schemes of embedded steel bars

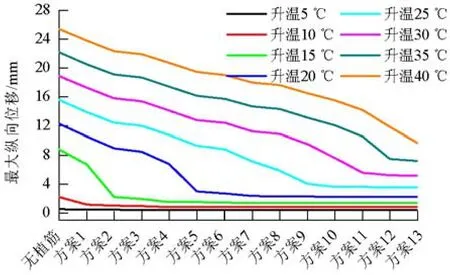
图10 不同升温幅度下不同植筋方案轨道板最大纵向位移Fig.10 Maximum longitudinal displacement of slab under different arrangement schemes of embedded steel bars and temperature

基于此原理，得到升温10～45℃时的最佳植筋方案，如表 4所示.其中，由于升温幅度超过30℃时，植筋限位效果不明显，因此未给出最佳方案.

考虑到实际操作方便性，不宜设置过多的植筋方案，因此建议:升温5～20℃时，推荐选择植筋方案5，即距离解锁自由端由近到远的第1、第2、第3块板分别植筋 16、8、8根;对于温升 20～30℃的情况，建议采取方案11，即距离解锁自由端由近到远的五块板分别植筋 16、16、16、10、8 根.

表4 计算所得植筋方案表Tab.4 Selected arrangement schemes of embedded steel bars 根

3 结论及建议

本文采用基于表面的内聚力模型模拟轨道层间黏结-脱黏-接触的复杂相互作用关系，并考虑剪力筋的非线性约束特性，建立了纵连板式无砟轨道层间抗剪性能分析模型，对比分析了有无植筋对轨道层间剪切破坏过程的影响以及不同升温幅度下合理植筋方案.主要结论如下:

(1)植筋可以明显提高砂浆层的抗剪性能.在本文条件下，植筋可将层间开裂时升温幅度由无植筋时的10.5℃提高到了30℃.

(2)当升温幅度超过30℃，各种植筋方案对轨道限位效果已不明显.因此，建议升温幅度超过30℃时，需结合其他措施进行限位.

(3)当升温幅度小于20℃，建议采用方案5(植筋16+8+8)，当升温幅度20～30℃之间，建议采用方案 11(植筋 16+16+16+10+8)，超过30℃，需辅助其他限位措施.

后续研究中将针对轨道界面参数开展系统测试(如文献［20］)，进一步对模型进行验证，并结合推板、揭板等相关试验对无砟轨道层间伤损机理进行更深入研究.

［1］ 王平，徐浩，陈嵘，等.路基上CRTSⅡ型板式轨道裂纹影响分析［J］.西南交通大学学报，2012，47(6):929-934.WANG Ping，XU Hao，CHEN Rong，et al.Effects analysis ofcrackingofCRTSⅡ slabtrackon subgrade［J］.Journal of Southwest Jiaotong University，2012，47(6):929-934.

［2］ GAUTIER P E.Slab track:review of existing systems and optimization potentials including very high speed［J］.Construction and Building Materials，2015，92:9-15.

［3］ 谭社会.高温条件下CRTSⅡ型板式无砟轨道变形整治措施研究［J］.铁道建筑，2016(5):23-27.TAN Shehui.Study on deformation treatment measures for CRTSⅡslab-type ballastless track in high temperature condition［J］. Railway Engineering，2016(5):23-27.

［4］ 廖红建，朱庆女，昝月稳，等.基于探地雷达的高铁无砟轨道结构层病害检测［J］.西南交通大学学报，2016，51(1):8-13.LIAO Hongjian，ZHU Qingnü，ZAN Yuewen，et al.Detection of ballastless track diseases in high-speed railway based on ground penetrating radar［J］.Journal of Southwest Jiaotong University，2016，51(1):8-13.

［5］ 曹世豪，杨荣山，刘学毅，等.无砟轨道层间裂纹内动水压力特性分析［J］.西南交通大学学报，2016，51(1):36-42.CAO Shihao，YANG Rongshan， LIU Xueyi， et al.Analysis of water pressure in ballastless track crack［J］.Journal of Southwest Jiaotong University，2016，51(1):36-42.

［6］ 苗雨.CRTSⅡ型板式无砟轨道高温胀板病害研究与整治［J］.科技创新与应用，2014(34):37-39.MIAO Yu.Study and treatment of upheaval of CRTS II type ballastless track［J］.Technology Innovation and Application，2014(34):37-39.

［7］ 倪跃峰，任娟娟，赵华卫.CRTSⅡ型板式无砟轨道抬板维修时轨道板锚固方案研究［J］.铁道建筑，2016(2):132-135.NI Yuefeng，REN Juanjuan，ZHAO Huawei.Study on anchoring scheme of lifted track slab in repairing of CRTS Ⅱ slab type ballastlesstrack［J］.Railway Engineering，2016(2):132-135.

［8］ 王继军.板式无砟轨道锚固销钉限位技术的试验研究［J］.铁道建筑，2010(6):122-125.WANG Jijun.Test research on anchoring technology of slab track［J］.Railway Engineering，2010(6):122-125.

［9］ 孙立.CRTSⅡ型板式无砟轨道结构温度变形控制措施研究［R］.武汉:中铁第四勘察设计院集团有限公司，2015.

［10］ 刘钰.CRTSⅡ型板式轨道早期温度场特征及其影响研究［D］.成都:西南交通大学，2013.

［11］ DAIG， SU M.Full- scale field experimental investigation on the interfacialshearcapacity of continuous slab track structure［J］.Archives of Civil and Mechanical Engineering，2016，16(3):485-493.

［12］ RAMAMURTHI M，LEE J S，YANG S H，et al.Delamination characterization of bonded interface in polymer coated steel using surface based cohesive model［J］. International Journal of Precision Engineering and Manufacturing， 2013， 14(10):1755-1765.

［13］ LIU G，BAO H，TANG K.Damage prediction in notched fiber- reinforced composite laminates［J］.Composite Interfaces，2016，24(3):279-290.

［14］ ZHANG M，ZUO C，SUN B，et al.Thermal ageing degradation mechanisms on compressive behavior of 3-D braided composites in experimental and numerical study［J］.Composite Structure，2016，140:180-191.

［15］ LUO C， LUA J， DESJARDIN P E. Thermomechanicaldamage modeling ofpolymer matrix sandwich composites in fire［J］.Composites Part A Applied Science and Manufacturing，2012，43(5):814-821.

［16］ 赵磊.高速铁路无砟轨道空间精细化分析方法及其应用研究［D］.北京:北京交通大学，2015.

［17］ 戴公连，粟淼.剪切荷载下板式无砟轨道界面黏结破坏机理［J］.华中科技大学学报:自然科学版，2016，44(1):16-21.DAI Gonglian，SU Miao.Mechanism of interfacial bond failure of slab ballastless track under shear loading［J］.JournalofHuazhong University ofScience and Technology: Natural Science Edition， 2016，44(1):16-21.

［18］ ZHU S，CAI C.Interface damage and its effect on vibrations of slab track under temperature and vehicle dynamic loads［J］.International Journal of Non-linear Mechanics，2014，58:222-232.

［19］ HARPER P W，HALLETT S R.Cohesive zone length in numerical simulations of composite delamination［J］.Engineering Fracture Mechanics， 2008， 75(16):4774-4792.

［20］ 王明昃，蔡成标，朱胜阳，等.基于黏聚力模型的双块式无砟轨道混凝土层间黏结性能试验与分析［J］.铁道学报，2016，38(11):88-94.WANG Mingze，CAI Chengbiao，ZHU Shengyang，et al.Experimental investigation on adhesive performance of concrete interface of double-block ballastless track based on cohesive zone model［J］.Journal of the China Railway Society，2016，38(11):88-94.