飞行时间质谱宽能量聚焦反射器设计

袁祥龙，李志明，翟利华，韦冠一，徐 江，汪 伟，沈小攀，王文亮，岳东宁

(西北核技术研究所，陕西 西安 710024)

飞行时间质谱技术因具有分析速度快、质量范围宽、灵敏度高、结构相对简单等特点而被广泛应用于同位素分析、蛋白质组学、基因测序以及化学物质检测等领域。如何提高分辨率是飞行时间质谱仪设计中的关键问题，而离子的初始空间和能量分布是影响飞行时间质谱分辨率的关键因素。1955年，Wiley等[1]论述了通过二级电场实现一阶空间聚焦的方法，以及通过延迟引出技术实现能量聚焦的方法。Seccombe等[2]沿用了这种空间聚焦方法，进一步对采用更多级电场实现更高阶的空间聚焦进行了深入的理论分析。Gardner等[3]提出了一种将多级电场引入离子源中实现空间聚焦的方法。1973年，Mamyrin等[4]将反射器引入飞行时间质谱仪中，通过实现能量聚焦，提高了质谱分辨率。理论上，电势随着距离呈平方关系变化的反射器能达到理想的能量补偿[5]。最常用的反射器通常采用二级电场实现二阶能量聚焦[4,6]。一般情况下，为了保证电场的均匀性，需在电极上加栅网，但这将降低离子的传输效率，因此也有研究团队尝试无网反射器设计[7-10]。

通常，反射式飞行时间质谱仪中首先利用推斥场和加速场在离加速区不远处实现一阶空间聚焦[11-12]，在该空间聚焦平面处，离子具有最小的空间分布。以此为起点，利用后面的自由飞行区和反射器实现能量聚焦。随着离子能量分散范围的不断增大，经典的二阶能量聚集反射器可实现的能量分辨率不断减小。为了提高飞行时间质谱在更大范围离子能量色散条件下的分辨率，Vlasak等[13]曾提出一种宽能量聚焦反射器的设计方法。该方法针对电极距离已经确定的反射器，对各电极的电压进行设计。本研究将在此基础上提出进一步的改进设计方案，采用数值计算对反射器电极距离和电极电压进行同时设计，希望能够更好地实现飞行时间聚焦性能。

1 二阶反射器参数设计

飞行时间质谱分辨率为：

(1)

式中，t0为离子飞行总时间，Δt为同一质量数的离子到达检测器的时间差。

为了降低Δt值，可以采用一阶或二阶能量聚焦方法。

1.1 一阶能量聚焦

使用最简单的一级反射器即可实现一阶能量聚焦。

设自由漂移区长度为L，反射场电场强度为E，离子初始能量为u0，并设U0q=u0，则离子飞行时间为：

(2)

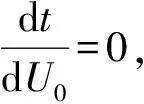
(3)

令L=1 m，u0=2 500 eV，则E=10 000 V/m。取质量数m=200，此时离子飞行时间与离子能量的关系示于图1。

在一定能量色散情况下，采用更高阶的能量聚焦方法可以实现更小的飞行时间差，进而获得更高的分辨率。在能量色散较小的情况下，二阶能量聚焦足以实现相当高的分辨率。

1.2 二阶能量聚焦

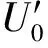
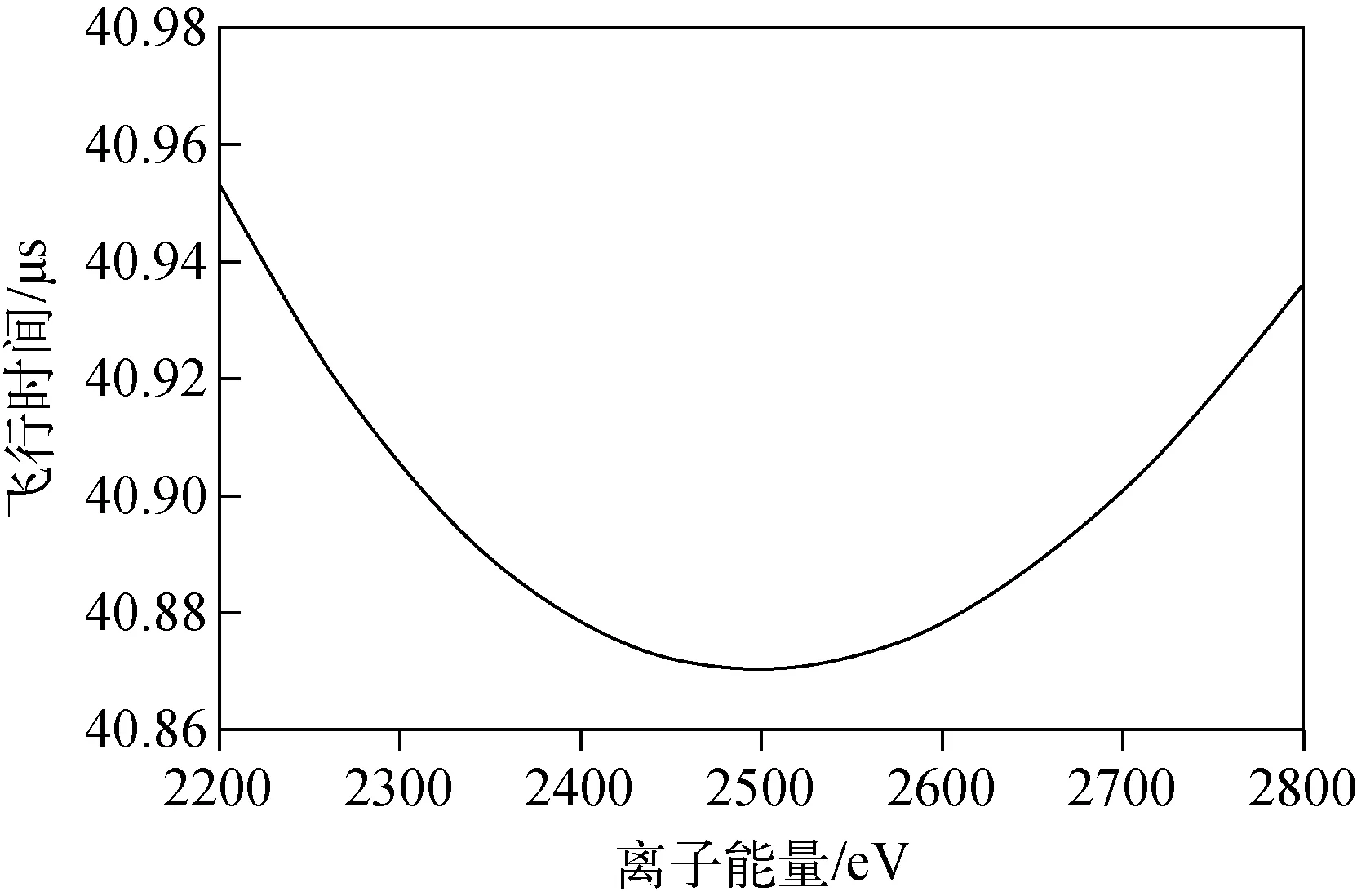
图1 一阶能量聚焦，离子飞行时间随离子能量的变化关系Fig.1 Relationship of flight time and ion energy at one-stage energy focusing

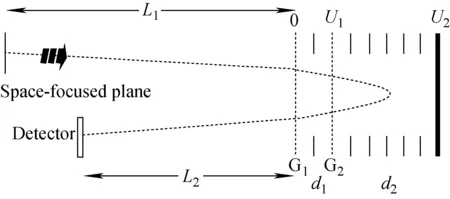
图2 二阶反射式飞行时间质谱部分结构示意图Fig.2 Partial structure of TOF MS with dual-stage ion reflectrons

为了实现二阶能量聚焦，文献[4]给出了一组近似的关系式：

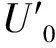
d1≈0.008L，d2≈0.06L

(4)

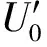
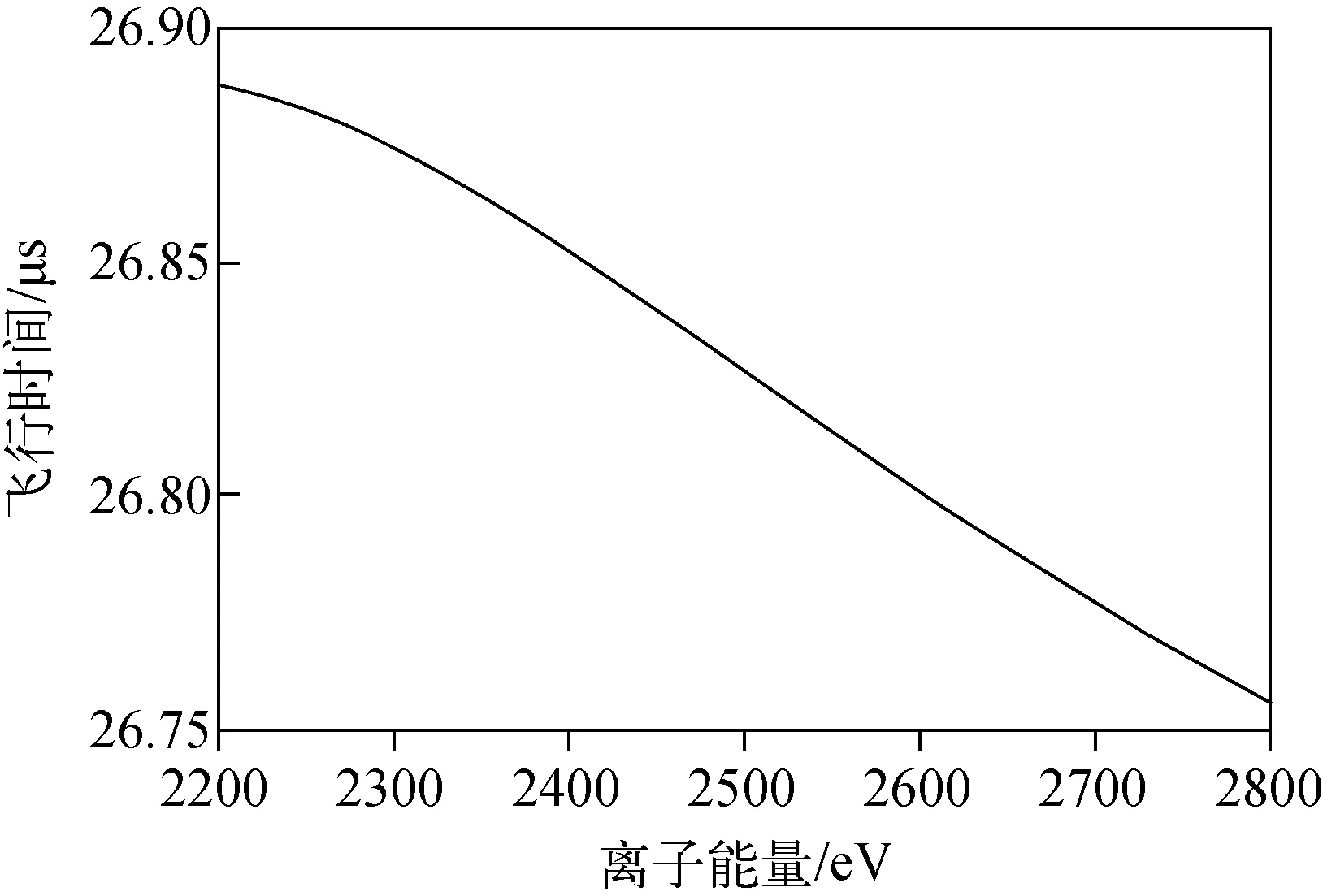
图3 采用公式(4)计算得到的离子飞行时间随离子能量的变化关系Fig.3 Relationship of flight time and ion energy calculated by formula (4)

虽然离子的飞行时间差很小，但仍可以确定该参数并未实现准确的二阶能量聚焦。

文献[6]曾详细讨论二阶反射器参数设计，本研究以d1和E2(第二级反射场电场强度)作为求解对象，推导出的二阶能量聚焦公式如下：

(5)

(6)

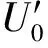
进一步计算得到的能量分散与分辨率的关系列于表1。可以看出，在相对能量色散较小的情况下，二阶能量聚集反射器可以实现较高的能量分辨率，但随着能量色散的不断增大，实现的能量分辨率将迅速下降。

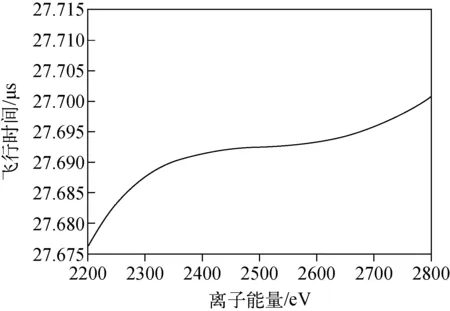
图4 采用公式(5)、(6)计算得到的离子飞行时间随离子能量的变化关系Fig.4 Relationship of flight time and ion energy calculated by formula (5) and (6)

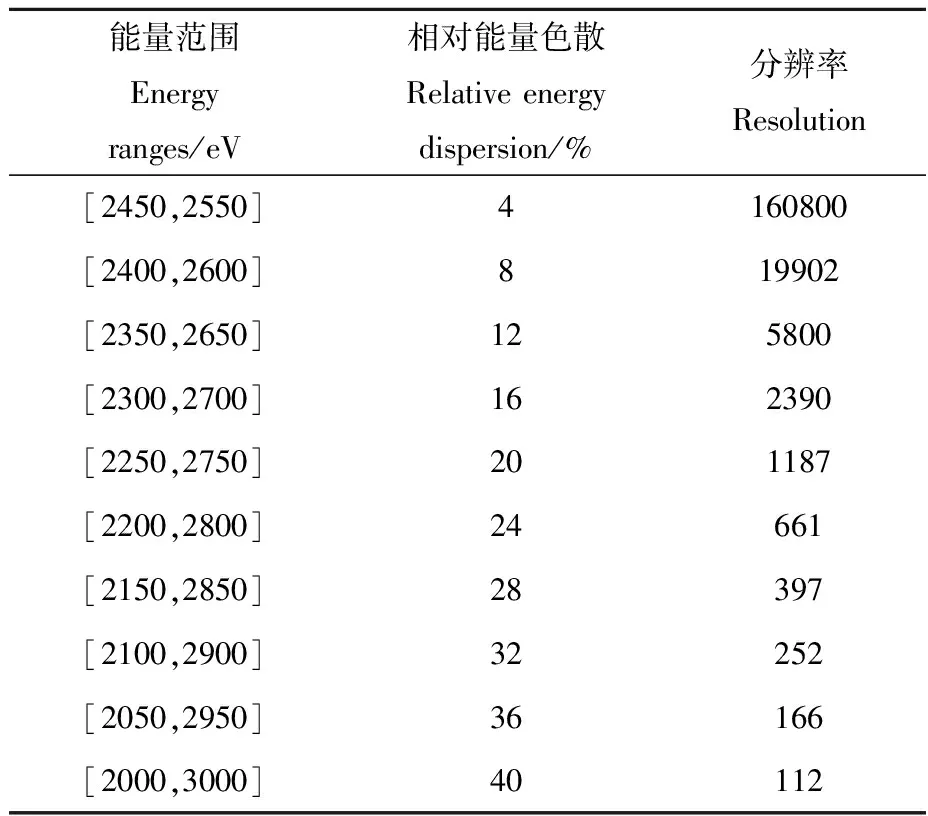
能量范围Energyranges/eV相对能量色散Relativeenergydispersion/%分辨率Resolution[2450，2550]4160800[2400，2600]819902[2350，2650]125800[2300，2700]162390[2250，2750]201187[2200，2800]24661[2150，2850]28397[2100，2900]32252[2050，2950]36166[2000，3000]40112

2 宽能量聚焦反射器的设计方法

为了在离子能量分散较大的情况下实现较高的能量分辨率，Vlasak等[13]提出了一种宽能量聚焦反射器的设计方法。由于文献中介绍该设计方法较完整的理论推导公式，本文不再重复。基本的设计思想是在给定反射器各电极间距的情况下，通过使从各电极处反射回去的离子的总飞行时间相等来确定各电极的电压。在离子束入射方向与反射器轴向夹角为2°的情况下，文献设计的反射器电极间距及计算得到的各电极电压列于表2。与其匹配的自由漂移区距离是188.6 cm。

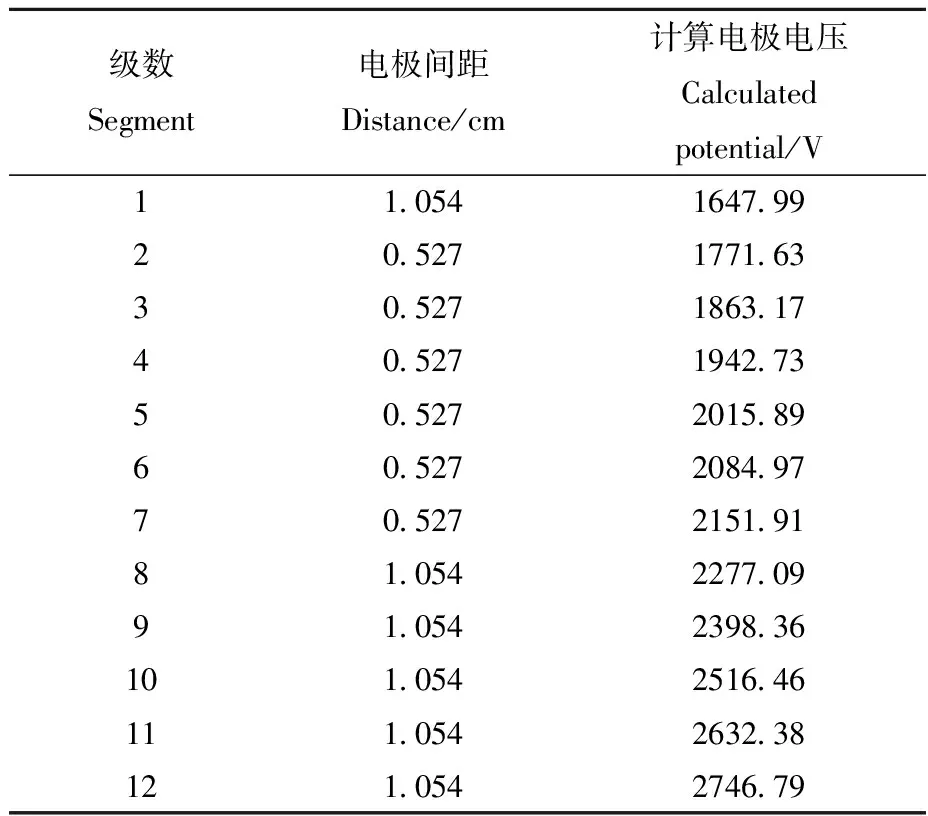
表2 文献中设计的宽能量聚焦反射器结构及电极电压Table 2 Broad energy range focusing reflectron segment configuration in the literature

针对以上结构，在质量数m=200时，计算得到离子飞行时间与离子能量的关系示于图5；分辨率的倒数(2Δt/t0)与离子能量的关系示于图6。

图5 根据文献[13]中宽能量聚焦反射器结构计算得到的离子飞行时间随离子能量的变化关系Fig.5 Relationship of flight time and ion energy according to the reflectron segment configuration in the literature[13]

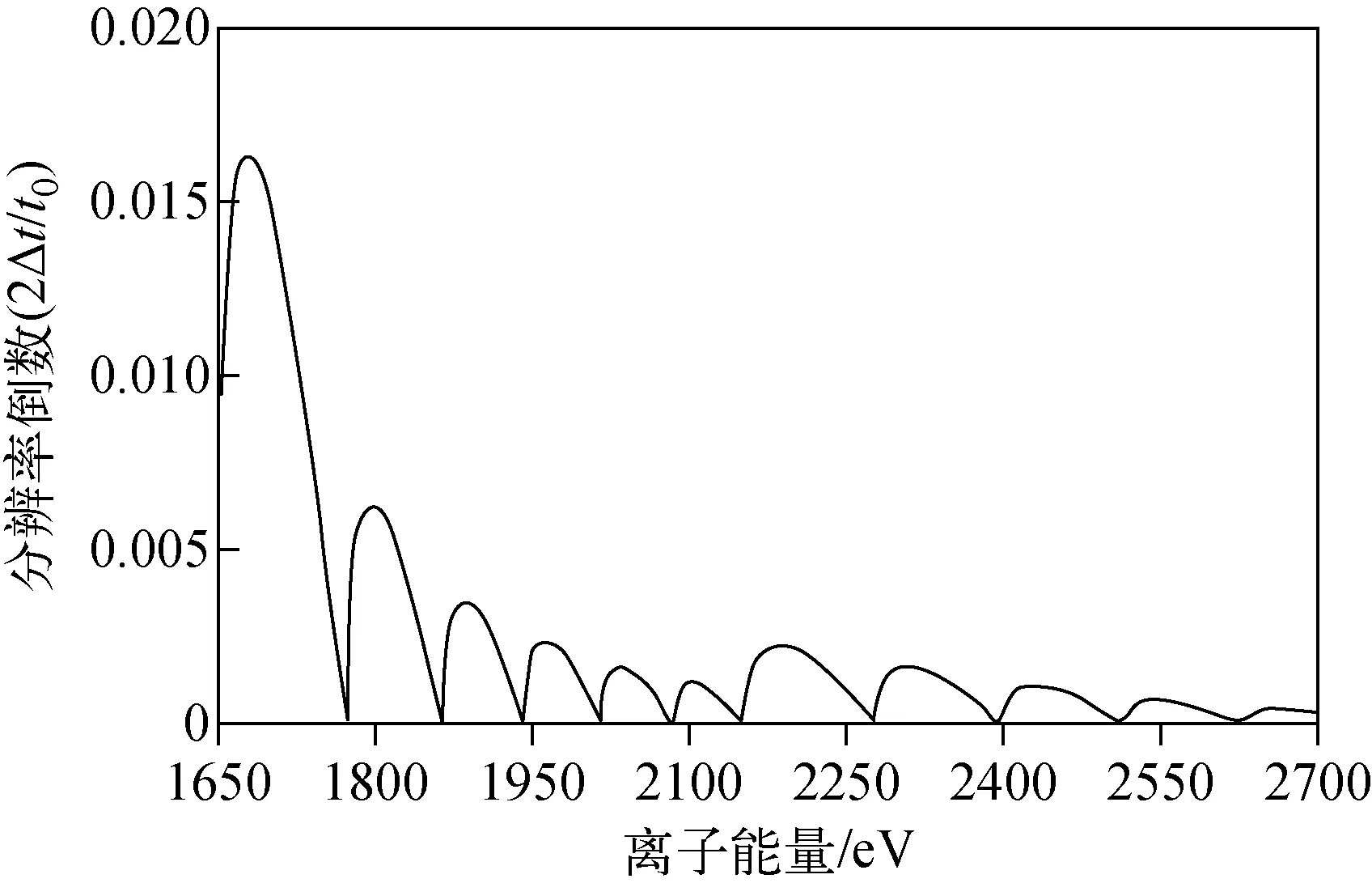
图6 根据文献[13]中宽能量聚焦反射器结构计算得到的分辨率倒数(2Δt/t0)随离子能量的变化关系Fig.6 Relationship of inverse resolution (2Δt/t0) and ion energy according to the reflectron segment configuration in the literature[13]

可以看出，当离子能量分布在1 950～2 700 eV时，能够达到的分辨率约为400。但该方法的缺点是从某一级反射场反射回去的离子的飞行时间差是不可控的，而分辨率则取决于飞行时间差最大的一级反射器。如何控制从每一级电场反射回去的离子的飞行时间差，是本研究提出改进方法的初衷。

进一步研究发现，针对能量最小的离子(能量记为Uminq)利用第一级反射场实现一阶能量聚焦或者利用前两级反射场实现二阶能量聚焦之后，选取合适的下一级反射场的电场强度，可以控制离子在该级反射场的最小飞行时间，即可控制该级反射场的飞行时间差。当离子的飞行时间再次等于最小能量的离子的飞行时间时(记此时离子的能量为Uiq)，即确定该级反射场后电极的电压为Ui。通过前后电极的电势差除以该级电场的电场强度，可以确定该级电场的长度。后续各级反射场电极的电压以及距离均依照该思路确定。而电场强度、电极电压以及电极间距离均依据上述设计思路采用数值计算的方法确定，其计算流程示于图7。

在自由漂移区长度L=1 m，需要聚焦的离子能量范围为2 000～3 000 eV时，实现分辨率为4 000，可以计算得到反射器需要13级，各极板间距及电压(以反射器第一块极板电压为参考零电位)列于表3。

根据表3中的计算电压可以得到反射器中电势分布与到反射器出口距离的关系，示于图8；分辨率的倒数(2Δt/t0)与离子能量的关系示于图9。

从图9可以看出，该反射器在离子能量色散为1 000 eV(相对能量色散为40%)时，实现了4 000的能量分辨率。

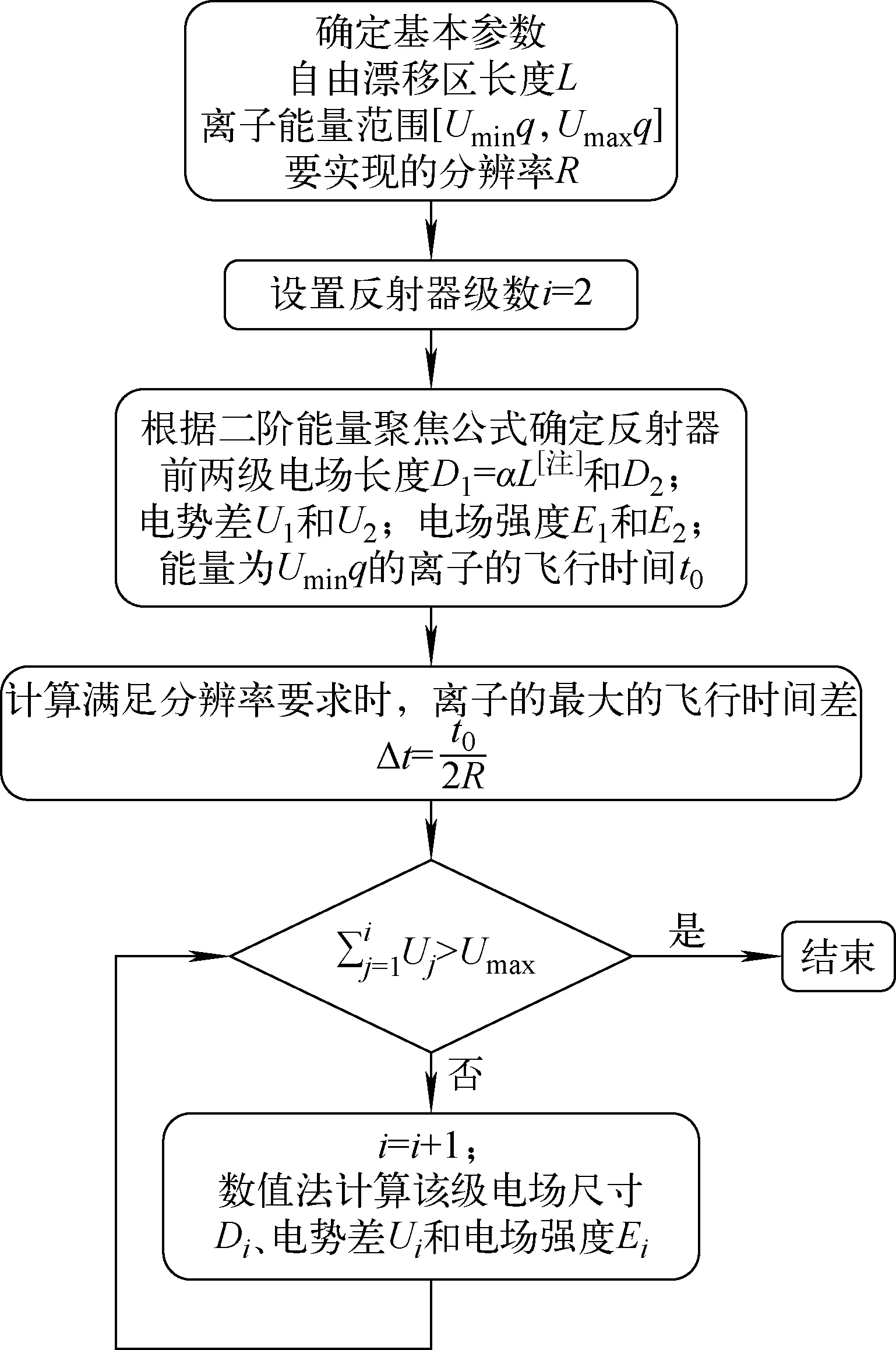
注：α<0.25，建议取α=0.01图7 本工作改进的宽能量聚焦反射器设计方法的计算流程图Fig.7 Flow chart to design the broad energy range focusing reflectrons in this paper

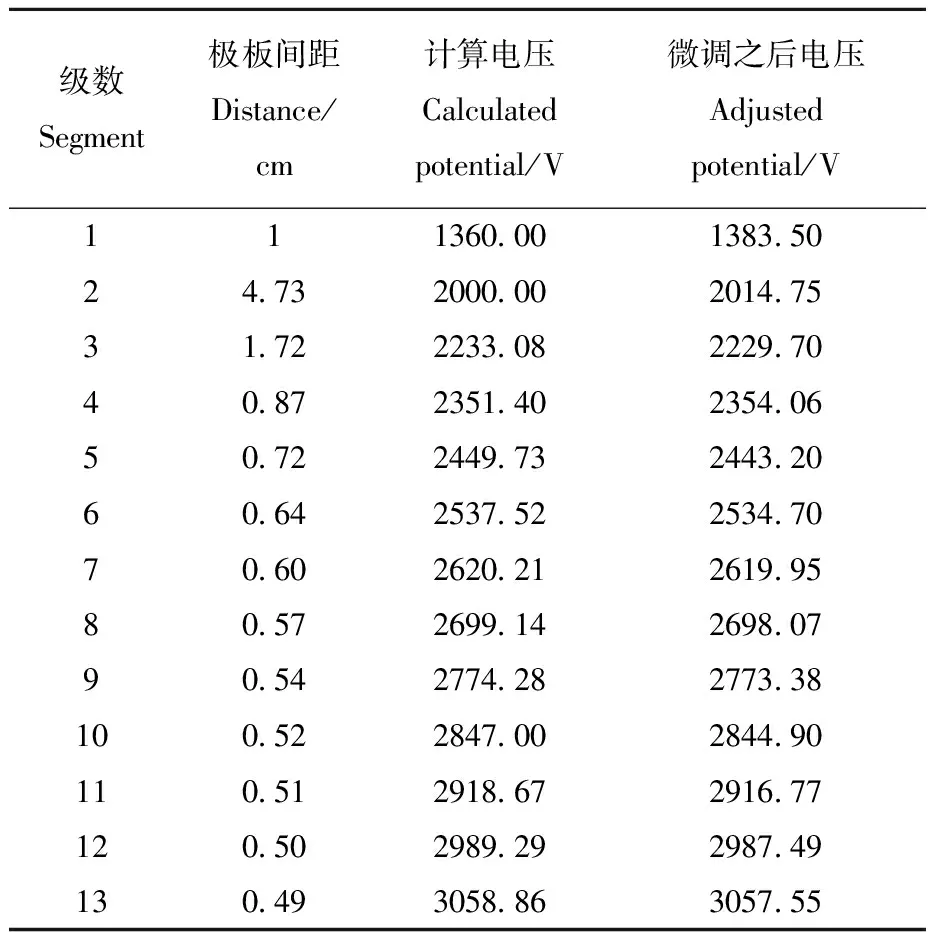
级数Segment极板间距Distance/cm计算电压Calculatedpotential/V微调之后电压Adjustedpotential/V111360001383502473200000201475317222330822297040872351402354065072244973244320606425375225347070602620212619958057269914269807905427742827733810052284700284490110512918672916771205029892929874913049305886305755

注：微调之后电压是指在只保留前两级栅网时，为补偿后续电场之间的渗透带来的影响而对电压进行了调整

图8 根据表3得到的反射器中电势分布与到反射器出口距离的关系Fig.8 Relationship of voltage and the distance to the exit of the reflectron configuration with table 3

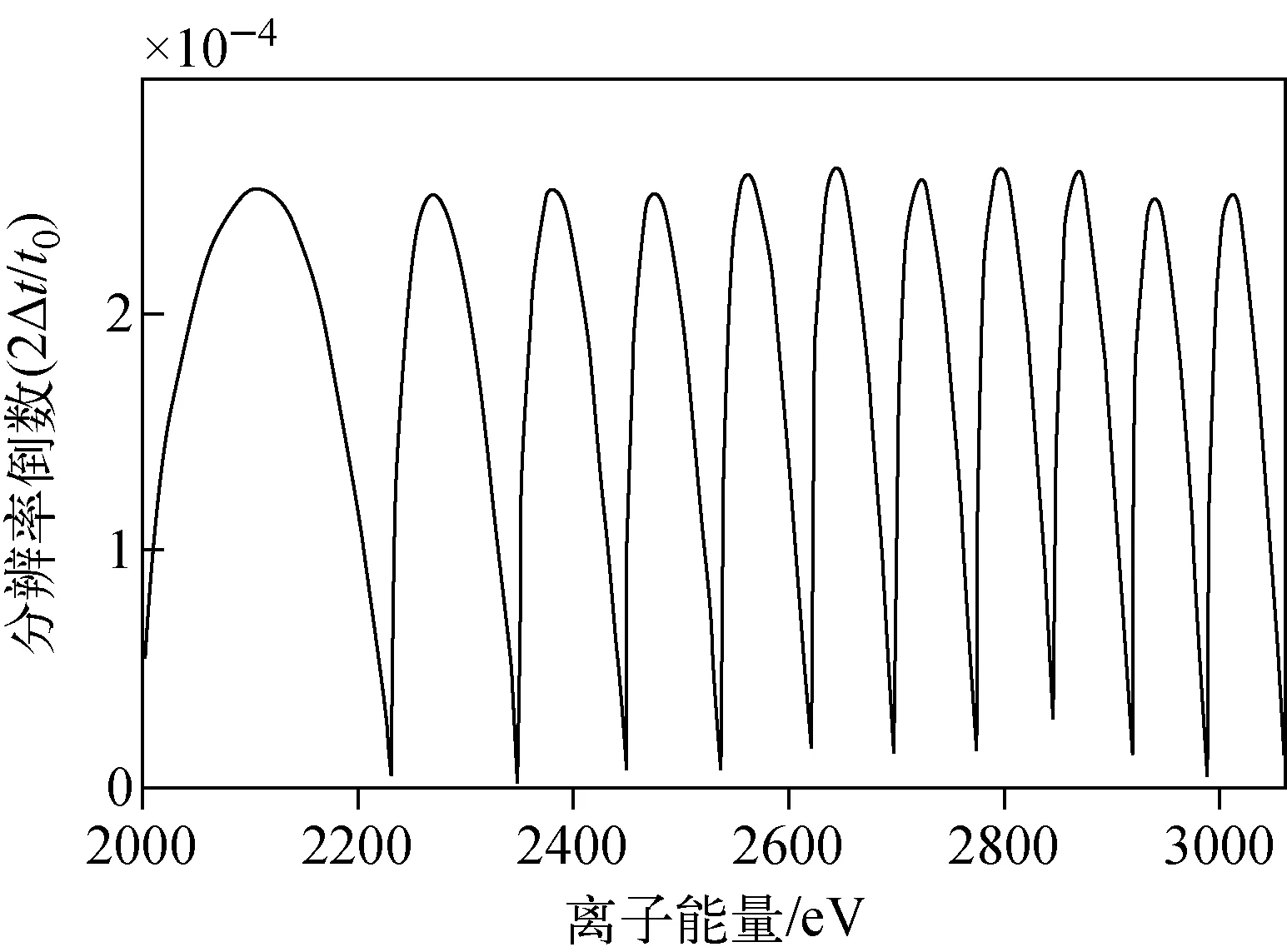
图9 根据表3得到的分辨率倒数(2Δt/t0)随离子能量的变化关系Fig.9 Relationship of inverse resolution (2Δt/t0) and ion energy according to the reflectron segment configuration with table 3

为降低本方法的实现难度，在对各级电场的长度计算中采用向下取整的方法保留至毫米量级。此时从各极板处反射回去的离子的飞行时间尚未达到最小能量的离子的飞行时间，因此飞行时间差仍在可控范围内。据此计算得到的反射器各极板间距及各极板应加载的电压列于表4，分辨率的倒数(2Δt/t0)与离子能量的关系示于图10。

值得注意的是，由于二阶聚焦的准确度对该方法的性能影响较大，因此没有对构成第二级电场的两极板间距进一步取整。

从表3和表4可以发现，在对极板间距进一步取整后，各极板上的电压有较小变化，但并没有导致分辨率的降低。这意味着间距的微小变化或装配偏差可以通过微调施加在极板上的电压补偿，这一特点降低了对机械加工和装配的精度要求。

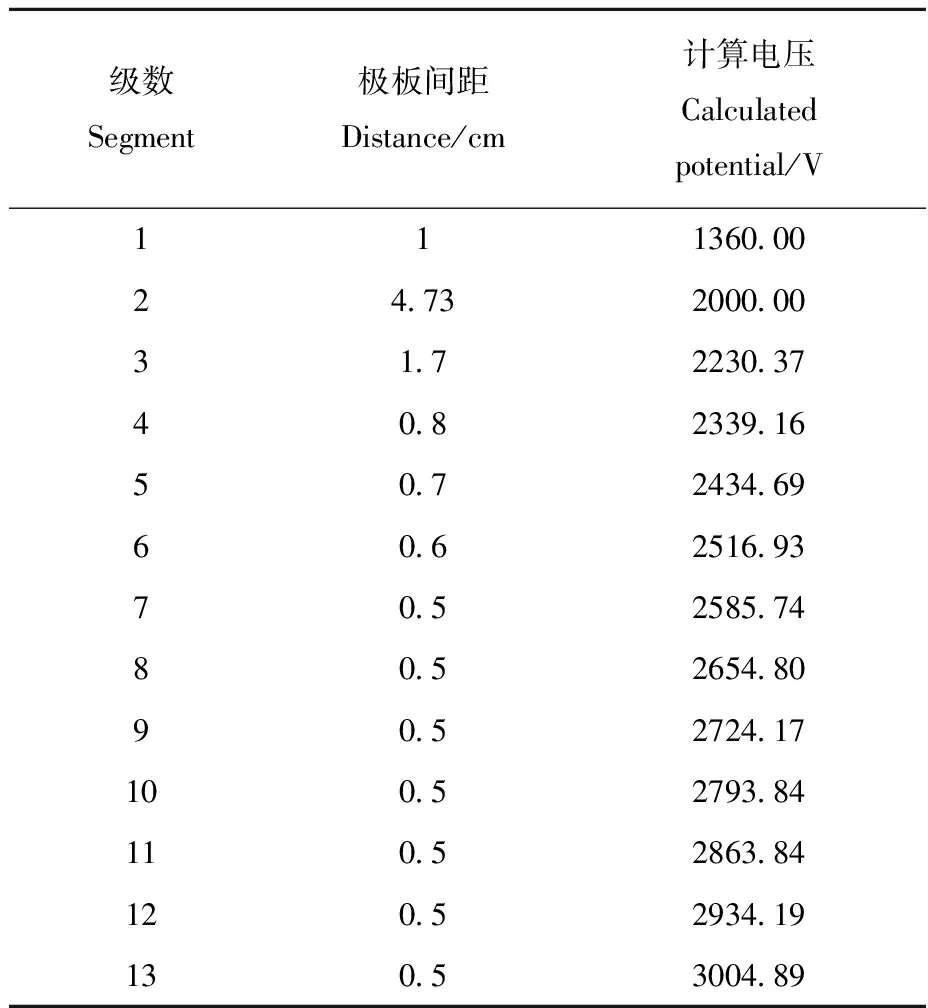
表4 采用本文设计的方法对电极距离进一步取整时的反射器结构和电极电压Table 4 Broad energy range focusing reflectron segment configuration with electrodes distance rounded to millimeter designed by the method in this paper

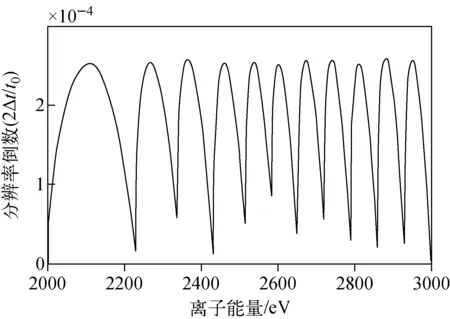
图10 根据表4得到的分辨率倒数(2Δt/t0)随离子能量的变化关系Fig.10 Relationship of inverse resolution (2Δt/t0) and ion energy according to the reflectron segment configuration with table 4

为了保证各级电场的均匀性，各电极上均需设置栅网，但设置的栅网越多，离子的传输效率越低。从图8可以看出，通过本方法设计的反射器，除第一级电场很强外，从第二级电场开始，后续电场比前级电场的强度只有微弱增强。因此，只需要保留前两级栅网以防止第一级电场与后续电场的相互渗透，而后面的各栅网均可去掉，此时后续电场之间只会有微弱的电场渗透，由此带来的影响也可以通过微调电极电压补偿。

3 仿真实验

针对表3中反射器结构，利用SIMION软件建立了3种仿真模型(仿真精度为0.2 mm/gu)，考察不同结构下反射器的等势线分布，其中相邻等势线的电势差为100 V。在模型1中，各电极均设置有栅网，将各电极电压设置为计算电压时，其等势线示于图11a，可以看出第一级电场强度远大于后续各级电场强度；在模型2中，除第一级栅网被保留外，其他所有电极的栅网均被取消，在加载了计算电压后，其等势线示于图11b，可以看出在取消了后续栅网之后，第一级电场对后续电场有强烈渗透，导致电场分布与设计目标有很大差别；保留前两级栅网，在加载对应电压后，等势线示于图11c，可以看出保留前两级栅网即可有效防止第一级电场向后续电场的渗透。

因为第二级电场及之后的各级电场间存在微弱的电场渗透，因此反射器中的电势分布与各电极均有栅网时的电势分布会有微小差异，为了减小由此带来的对飞行时间聚焦的影响，需要在实际中通过微调电压予以补偿。在SIMION仿真中，设置离子飞行的起点与检测器均距离反射器50 cm，离子飞行方向与轴线夹角为2°，能量在2 000～3 000 eV之间均匀分布。在对反射器各电极电压进行微调后，仿真得到的离子轨迹示于图12。在仿真过程中，每隔2 μs记录一次离子到达的位置。可以看出，不同能量的离子分布先随飞行时间的增加而扩大，经过反射器反射后，在到达探测器的过程中又不断缩小。

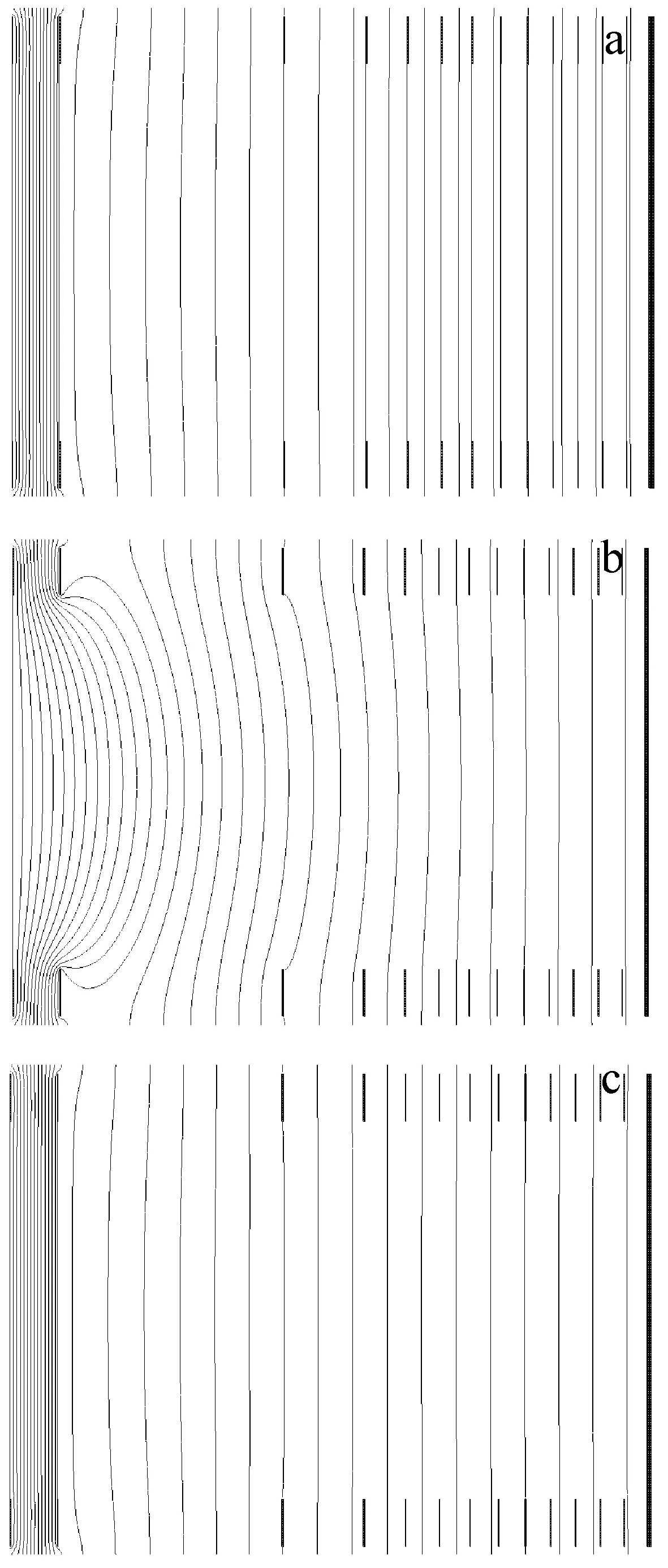
注：a.各电极均有栅网；b.仅保留第一级栅网；c.保留前两级栅网图11 不同配置下的反射器等势线分布 Fig.11 Contour lines of the reflectrons with different configuration

图12 反射器只保留前两级栅网SIMION仿真结果Fig.12 SIMION simulation when the first two electrodes were reserved

统计得到的离子飞行时间与离子能量的关系示于图13。

此时，达到的分辨率(t0/2Δt)约为2 000。之所以没达到4 000的分辨率，主要有以下几点原因：1)由于个人计算机内存限制，仿真精度只有0.2 mm/gu，而在计算过程中的精度保留至0.1 mm；2)电极存在厚度，因此会带来一定的弥散场影响电场分布，但与二阶能量聚焦在[2000 eV，3000 eV]的分布下只能达到100的分辨率相比，也足以体现出该方法的意义。

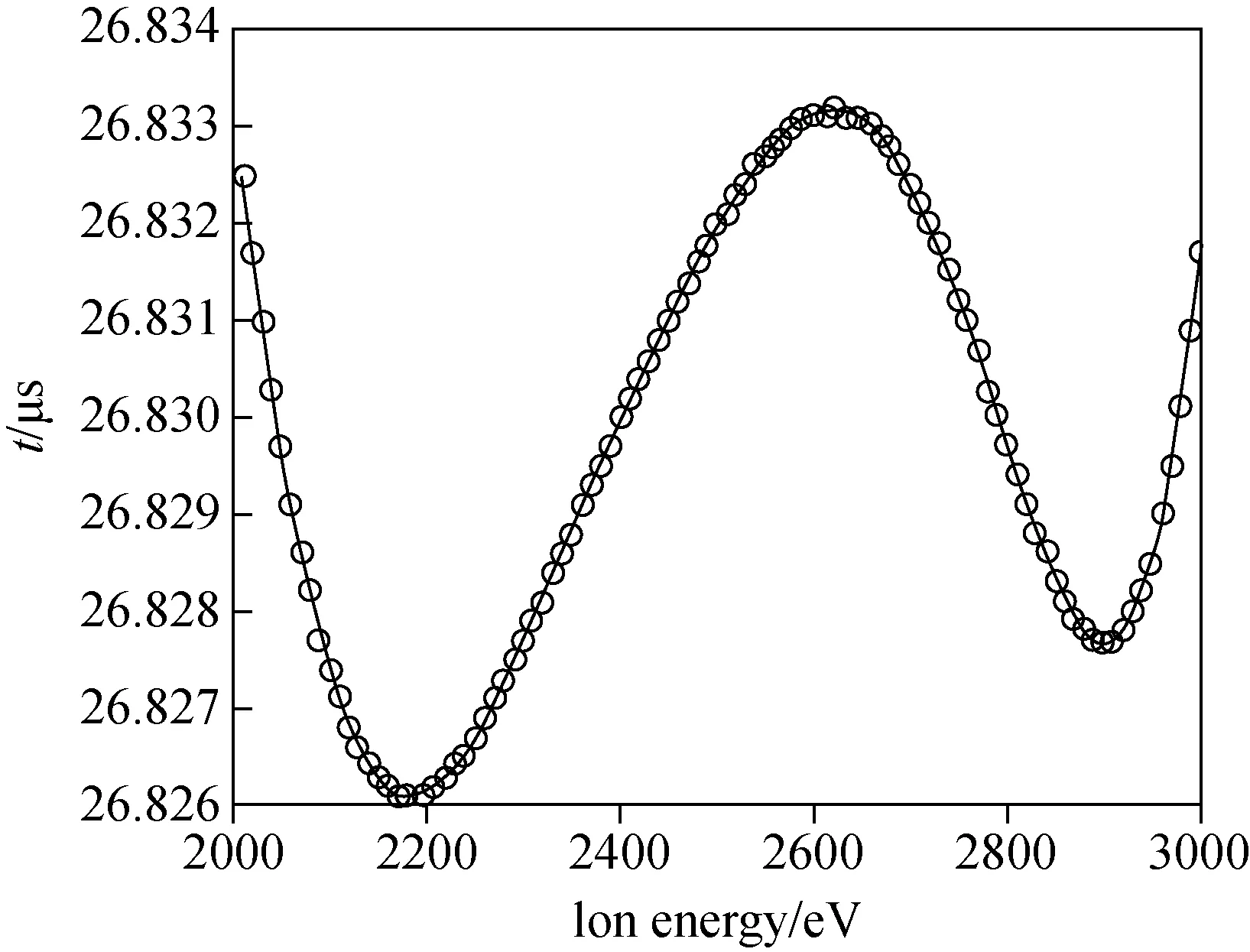
图13 仿真得到的离子飞行时间随离子能量的变化关系Fig.13 Relationship of flight time and ion energy in the SIMION simulation

4 结论

本研究针对Vlasak的宽能量聚焦反射器的设计方法提出了一种改进方案。通过同时对反射器各级长度和各极板所加载的电压进行设计，能够更有效地提高在离子能量分布范围较大的情况下的飞行时间质谱分辨率。为了提高离子传输效率，在仿真模型中只保留了前两级栅网，通过对电极电压进行微调，可有效减小电场渗透带来的影响。

[1] WILEY W C, MCLAREN I H. Time-of-flight mass spectrometer with improved resolution[J]. Review of Scientific Instruments, 1955, 26(12): 1 150-1 157.

[2] SECCOMBE D P, REDDISH T J. Theoretical study of space focusing in linear time-of-flight mass spectrometers[J]. Review of Scientific Instruments, 2001, 72(2): 1 330-1 338.

[3] GARDNER B D, HOLLAND J F. Nonlinear ion acceleration for improved space focusing in time-of-flight mass spectrometry[J]. Journal of the American Society for Mass Spectrometry, 1999, 10(11): 1 067-1 073.

[4] MAMYRIN B A, KARATAEV V I, SHMIKK D V, et al. The mass-reflectron, a new non-magnetic time-of-flight mass spectrometer with high resolution[J]. Journal of Experimental & Theoretical Physics, 1973, 37(1): 45-48.

[5] MAMYRIN B A. Time-of-flight mass spectrometry (concepts, achievements, and prospects)[J]. International Journal of Mass Spectrometry, 2001, 206(3): 251-266.

[6] WANG T I, CHU C W, HUNG H M, et al. Design parameters of dual-stage ion reflectrons[J]. Review of Scientific Instruments, 1994, 65(5): 1 585-1 589.

[7] BIMURZAEV S B. A time-of-flight mass reflectron with controlled ion-energy spread in the packet generated by an ion source[J]. Technical Physics Letters, 2014, 40(2): 108-111.

[8] KUTSCHER R, GRIX R, LI G, et al. A transversally and longitudinally focusing time-of-flight mass spectrometer[J]. International Journal of Mass Spectrometry & Ion Processes, 1991, 103(s2/s3): 117-128.

[9] ZHANG J, ENKE C G. Simple cylindrical ion mirror with three elements[J]. Journal of the American Society for Mass Spectrometry, 2000, 11(9): 759-764.

[10] ZHANG J, GARDNER B D, ENKE C G. Simple geometry gridless ion mirror[J]. Journal of the American Society for Mass Spectrometry, 2000, 11(9): 765-769.

[11] GUILHAUS M. Principles and instrumentation in time-of-flight mass spectrometry[J]. J Mass Spectrom, 1995, 99(11): 1-39.

[12] GUILHAUS M, MLYNSKI V, SELBY D. Perfect timing: time-of-flight mass spectrometry[J]. Rapid Communications in Mass Spectrometry, 1997, 11(9): 951-962.

[13] VLASAK P R, BEUSSMAN D J, JI Q, et al. Method for the design of broad energy range focusing reflectrons[J]. J Am Soc Mass Spectrom, 1996, 7(10): 1 002-1 008.