基于EEMD的单通道机械噪声信号盲分离

侯一民，张荣彬

（东北电力大学 自动化工程学院，吉林 132000）

0 引言

机械噪声和振动信号中蕴含大量可以反映设备运行状态的信息，对这些信号进行分析能达到对设备状态进行监测以及故障预判的目的。目前，利用振动信号进行故障诊断应用较广[1,2]。但在某些特殊工况（高温、腐蚀、无法停机等）[3]下，不易采集振动信号时，考虑利用噪声信号进行故障诊断具有一定优势。对于多个设备产生的混合噪声信号，传统的信号分析方法很难处理，盲源分离（Blind Signal Separation，BSS）[4]应用到混合信号处理中，可以获得各个源信号，进而实现对具体设备的状态监测与故障诊断。同时，受现场环境与设备造价的影响，采用单个传感器采集信号实现盲源分离的情况时有发生，这种单通道的盲源分离更具有实际研究价值。

解决机械信号单通道盲分离，毋文峰等[5]将经验模态分解（Empirical Mode Decomposition，EMD）与Fast-ICA结合用于机械故障诊断，但是采用EMD存在模态混叠现象。为此，孟宗等[6]将集合经验模态分解（Ensemble EmpiricalMode Decomposition，EEMD）[7]与JADE结合用于机械振动信号的单通道盲分离，EEMD较EMD能有效抑制了模态混频现象。本文在已有的研究基础上对单通道机械噪声信号进行处理，利用EEMD分解混合信号得到一系列本征模态函数（Intrinsic mode function，IMF）分量，这样非线性、非平稳的机械信号就变成了线性、平稳的信号了[8,9]。然后进行源数目估计，并根据估计出的源信号数目，选取合适的IMF分量重构观测信号，最后利用Fast-ICA算法恢复源信号，并通过三台异步电动机噪声信号分离验证方法有效性。

1 盲源分离模型

1.1 传统BSS模型

设系统在t时刻有m×1阶观测信号列向量，描述为：x(t)=[x1(t)，x2(t)，…，xm(t)]T，有n×1阶源信号列向量，描述为：s(t)=[s1(t)，s2(t)，…，sn(t)]T，则线性瞬时混合模型可描述为：

式中的A=[a1(t)，a2(t)，…，an(t)]是mxn阶的满秩混合矩阵，aij是混合系数；v(t)=[v1(t)，v2(t)，…，vm(t)]T是mx1阶加性噪声。当不考虑噪声影响或通过一定方法将噪声降到很小可以忽略不计，此时的数学模型为：

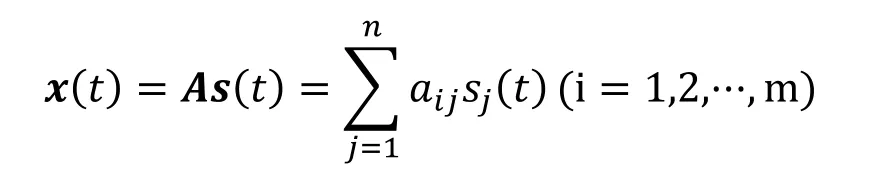
式中除了x(t)，s(t)和A都是未知的，此时求盲源分离问题需要构建一个n×m阶分离矩阵W，使得观测信号x(t)经过W线性变换后得到n×1阶输出列向量y(t)=Wx(t)=WAs(t)（分离模型），若求得W=A-1，则有y(t)=s(t)，以此来恢复源信号或对源信号进行估计。

1.2 单通道盲分离模型

假设系统在t时刻有n个独立源信号描述为S(t)=[s1(t)，s2(t)，…，sn(t)]T，该n个源信号由一个传感器所接收，表示为X(t)，则单通道盲源分离数学模型可描述为：

其中n为源信号数目，aj为加权系数，sj(t)为第j个源信号，v(t)是与源信号相互独立的高斯白噪声信号。单通道盲源分离的

任务即从单观测信号X(t)中通过盲源分离算法恢复各独立源信号。

2 基于EEMD的单通道盲分离

2.1 EEMD算法

利用EEMD可以有效改善EMD分解观测信号时的模态混叠现象[7,10]，其算法步骤如下[11]：

1）在原始单观测信号x(t)中多次添加均值为零、长度相等的高斯被噪声信号v(t)；

2）对加入高斯白噪声的x(t)信号进行EMD分解得到一系列IMF分量，其中最后一个分量为余项；

3）重复执行前两步N次，要求每次执行加入新的高斯白噪声；

4）通过计算不含余项的所有IMF分量的均值以抵消N次加入的高斯白噪声，并将该均值作为EEMD最终分解结果。

2.2 源数估计

为实现单通道机械噪声信号盲分离，需估计系统中源信号数目。文献[12]提出基于EMD-SVD的源数估计方法，本文在此基础上提出用EEMD-SVD方法估计源数目，该方法步骤如下：

1）对单通道观测信号x(t)的分别进行EEMD分解，得到IMF分量；

2）将x(t)与IMF组合后求其相关矩阵，并相关矩阵进行奇异值分解；

3）剔除特征值为0的元素，特征值序列从大到小排列，求相邻特征值的最大比值：

4）根据邻近比的最大值确定源信号的数目。

2.3 基于EEMD的单通道机械噪声信号盲源分离

基于以上分析，采用EEMD-FastICA方法进行噪声信号分离，本文具体工作如下：

1）单观测信号x(t)进行EEMD分解，得到一系列IMF分量：ximf(t)=[c1(t)，c2(t)，…，cn(t)，rn(t)]T。

2）源数目估计。利用2.2小节的EEMD-SVD方法，根据特征值占优比估计原信号数目。

3）构造新的观测信号。首先选取合适的IMF分量，将每个IMF分量与原单通道混合信号分别求相关度，并取出相关度较大的IMF分量；然后根据估计的源数目，选取合适的IMF分量与源信号组成新的多维观测矩阵，使新观测矩阵维数等于源信号数。

4）对新的观测信号利用Fast-ICA算法恢复源信号。

基于EEMD的单通道机械噪声信号盲源分离具体实现流程如图1所示。

图1 基于EEMD的单通道机械噪声信号盲源分离

3 实验研究

选择三台异步电动机的转动声音信号作为实验数据，三台电动机的转速不同，采用单声道16位采样，采样频率4.41kHz，采样点数60000。图2是噪声源信号波形，图3是用单个传感器观测到的混合信号波形。

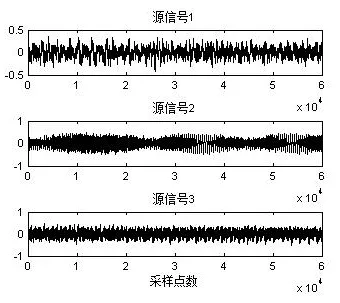
图2 源信号

图3 单通道混合信号

3.1 源数估计

对单通道信号进行EEMD分解，利用2.2小节中的方法进行源数估计。得到14个特征值分别为：2.5220，2.1987，1.8622，1.3934，1.3196，1.1517，1.0647，0.9543，0.8047，0.7603，0.7001，0.6678，0.5356，0.4334。根据相邻特征值最大，如图4可知，第3个与第4个特征值之间下降最快，可知占优特征值数目为3，所以估计源信号数目为3。

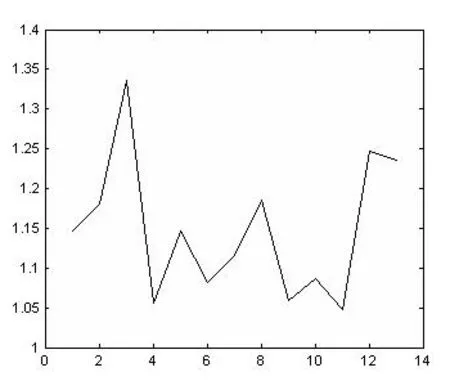
图4 特征值邻近比图

3.2 盲源分离

根据计算出的各个IMF分量与单通道信号的相关度，按照信号接近程度以及估计出的源信号数目，选出IMF7和IMF8两个分量，与单观测信号组成新的多维矩阵x1=[x，imf7，imf8]T，这样，欠定的单通道盲源分离问题就转变成正定的多通道盲源分离了，从而可以利用传统盲分离算法恢复源信号。分量IMF7和IMF8波形图及频谱图如图5所示。图6是利用经典盲分离Fast-ICA算法分离得到的三个源信号。

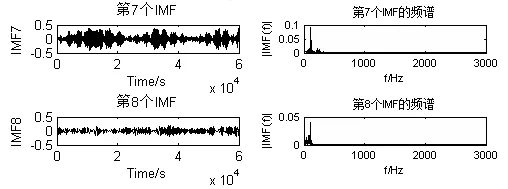
图5 IMF7和IMF8分量

图6 分离信号

根据图6可知，分离出的三个信号排序与波形幅值均有变化。由于盲源分离具有排序与幅值的不确定性，因此这些变化并不影响分离结果[13]。为了考察信号的分离效果，在此利用相关系数[14,15]作为评价标准评价分离结果，分别对每一个分离信号求与源信号的相关度，结果如ρ矩阵中的数据。矩阵中，ρij表示第i个分离信号与第j个源信号的相关度。

可见，分离信号1与源信号2、分离信号2与源信号3、分离信号3与源信号1的相关系数绝对值均接近1，表明分离效果较理想。由此也可以判断出分离信号与源信号的对应关系。

4 结束语

本文研究了单通道机械噪声信号的盲源分离问题，给出具体实现过程，并通过真实实验进行研究，从三台异步电动机混合噪声信号中成功地分离出各个源信号。

单通道机械噪声信号的分离，可为后续信号分析奠定基础，为利用机械噪声信号进行故障诊断提供新的思路。

[1]朱会杰,王新晴,芮挺,等.基于移不变稀疏编码的单通道机械信号盲源分离[J].振动工程学报,2015,28(4)：625-632.

[2]Nguyen V H, Rutten C, Golinval J C. Fault diagnosis in industrial systems based on blind source separation techniques using one single vibration sensor[J].Shock & Vibration,2012,19(5)：795-801.

[3]王宇.机械噪声监测中盲信号处理方法研究[D].昆明理工大学,2010.

[4]Jutten C,Herault J. Blind separation of sources, Part I： an adaptive algorithm based on neuromimeticarchitecture[J].Signal Processing.1991,24：1-10.

[5]毋文峰,陈小虎,苏勋家.基于经验模式分解的单通道机械信号盲分离[J].机械工程学报,2011,47(4)：12-16.

[6]孟宗,蔡龙.基于EEMD子带提取相关机械振动信号单通道盲源分离[J].振动与冲击,2014,33(20)：40-46.

[7]WU Z,HUANG N E.Ensemble empirical mode decomposition：A noise-assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1)：1-41.

[8]王丽,周以齐,于刚,等.基于EEMD和ICA方法的驾驶室内噪声源时频分析[J].山东大学学报：工学版,2014(2)：80-88.

[9]孟宗,顾海燕.基于盲源分离去噪和HHT的旋转机械故障诊断[J].计量学报,2013,34(3)：242-246.

[10]郑近德,潘海洋,张俊,等.APEEMD及其在转子碰摩故障诊断中的应用[J].振动、测试与诊断,2016,36(2)：257-263.

[11]Sweeney K T, Mcloone S F, Ward T E. The use of ensemble empirical mode decomposition with canonical correlation analysis as a novel artifact removal technique[J].IEEE transactions on biomedical engineering,2013,60(1)：97-105.

[12]谭北海,谢胜利.基于源信号数目估计的欠定盲分离[J].电子与信息学报,2008,30(4)：863-867.

[13]Li J, Zhang Y X, Li L. Study on separation of the vibration response of diesel based on the blind source separation[J].Chinese Internal Combustion Engine Engineering,2009,30(3)：61-64.

[14]刘佳,杨士莪,朴胜春,等.单观测通道船舶辐射噪声盲源分离[J].声学学报,2011(3)：265-270.

[15]Benesty J, Chen J, Huang Y. On the Importance of the Pearson Correlation Coefficient in Noise Reduction[J].IEEE Transactions on Audio Speech & Language Processing,2008,16(4)：757-765.