点云模型行距自适应数控加工刀轨生成方法研究

刘 威，朱淑梅，周 琛，沈晔湖，张彤彤

（苏州科技大学 机械工程学院，苏州 215000）

0 引言

逆向工程与数控加工相结合进行产品制造的过程通常是先通过测量设备获取实物模型表面点云模型，再对点云进行一系列处理，最后生成数控加工刀轨进行加工，特别适合复杂实物和难以获得数字模型的产品。点云生成刀轨常使用等间距行切法，为了使加工后残留高度不大于阈值（即最大允许值），行距设置通常较为保守，导致刀轨总长度较大，因此在满足残留高度要求的前提下，可根据点云轮廓求出每一行最大行距（即行距自适应），以减少刀轨行数和刀轨总长度。

计算自适应行距需要先计算出刀位点的残留高度点，再根据残留高度点和局部点云计算出下一行刀位点，两刀位点之间的距离即为满足残留高度的最大行距，所运用的原理、方法与等残留高度刀轨生成基本一致。目前的研究成果主要集中在网格和曲面上[1～6]，然而点云由于其离散性，这些算法难以直接应用。吴福忠[7,8]对点云划分四边形网格模型[7]，提出等距获得残留高度曲面和刀位面、对等距面与刀具包络面求交获取等残留高度线和刀位点的方法，类似方法也被应用在规则点云中[8]。然而等距法难以适用于离散点云，为此作者对离散点云提出了无需对点云进行等距求交、根据点云局部轮廓和刀具模型直接生成等残留高度刀轨的方法[9]，但计算效率较低。文献[10]针对局部点云修改后重新生成的刀轨，给出了残留高度是否超过阈值的判断方法，通过新增刀轨满足残留高度，但难以做到行距最大化。

目前的研究成果主要存在计算过程依赖点云等距[7,8]、计算量大[9]、难以实现行距理论最大化[10]的问题，为此本文提出无需点云等距直接计算残留高度点和下一行刀位点的方法，在已有成果基础上[9]，为了提高计算效率同时保证精度，采用预设初值、迭代逼近的方法计算出满足精度的残留高度点和刀位点，计算过程中只对密切相关的数据点进行计算并逐步剔除无关数据点，以减少计算量。算法结构紧凑、效率高，实现了对离散点云行距自适应刀轨的生成。

1 行距自适应刀轨计算

1.1 构建局部坐标系

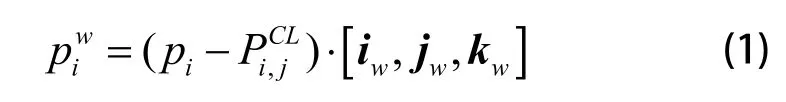
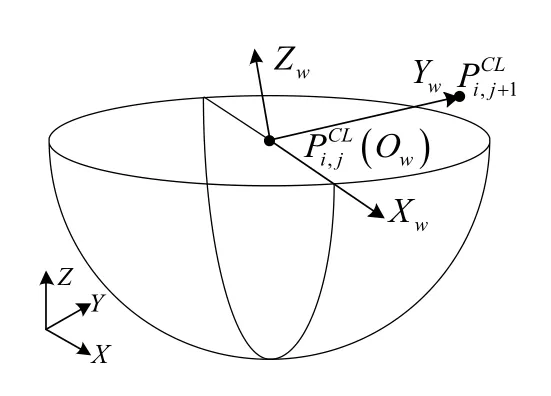
图1 局部坐标系OwXwYwZw 示意图

1.2 计算残留高度点

在坐标平面XwOwZw上，残留高度点位于刀具圆上，其位置由残留高度阈值h和点云局部轮廓共同决定。由于点云的离散性，若严格以点云位于XwOwZw平面上的点作为交线，不可能获取真实轮廓，为此采用作者已有的点云切片算法[11]对满足式(2)的点计算出刀位点附近的截面轮廓点集其中xw为局部坐标，R为刀具半径，δ为切片厚度。

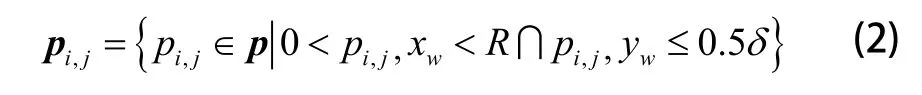
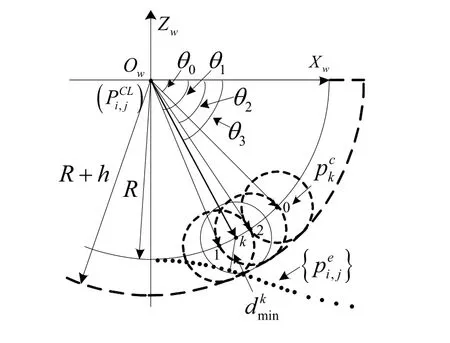
图2 计算残留高度点示意图

如图2所示，构造以Ow为圆心的刀具圆，要求的残留高度点位于第四象限的刀具圆上，其几何意义为相邻行刀具圆相交于此点时，两刀具圆与点云轮廓所组成区域为未加工的残留区域，残留高度点到点云轮廓的最小距离dmin等于预设的残留高度阈值h。为了避免通常所采用的较为繁琐的等距求交方法，本节提出一种无需等距、根据点云局部轮廓直接求出残留高度点的方法。

为了提高计算效率同时满足精度值eh要求，提出计算残留高度值在范围内的残留高度点。由于圆上任意一点可由极角θ定义，因此可通过预设初值、迭代逼近的方式计算残留高度点的极角，流程如下：

Step 4：令θk+1=θk-Δθk，其中转到Step 2。

Step 5：极角kθ对应的圆上点满足精度要求，由式(1)转换为全局坐标，即为残留高度点重复以上流程可求出当前行所有刀位点的残留高度点。

1.3 计算下一行刀轨的行距

图3 计算下一行刀位点示意图

如图3所示，以残留高度点psc为原点Os构建局部坐标系OsXsYsZs，坐标轴与局部坐标系OwXwYwZw相同，构造Os为圆心的刀具圆，要求的下一行刀位点位于第一象限的刀具圆上，其几何意义为以为刀位点的刀具几何体与局部点云相切，即中的点与的最小距离dmin为R。局部点云可由式(3)求出并保存坐标系OsXsYsZs下的坐标。

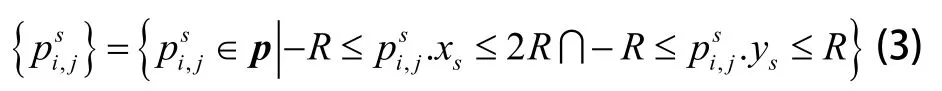
为了提高计算效率，与残留高度点计算类似，本节将计算最小距离为自定义的误差值）的刀位点，同样采用预设初值、迭代逼近的方式计算刀位点的极角，流程如下：

2 算例

本文所提出的方法已在Visual C++ 6.0和Opencascade6.2.0平台上完成了软件的开发，为验证其可行性，以图4(a)中的马鞍形点云为例生成行距自适应刀轨。点云包围盒尺寸为200×200×112（单位为mm，下同），包含1,000,000个点，刀具为直径20的球头刀，残留高度为0.2，残留高度点和刀位点的计算精度均为0.01。图4(b)为生成的行距自适应刀轨，其行距范围为4.14～6.82。作为对比，采用等间距规划刀轨，取最理想行距4.14（即行距自适应中的最小行距）生成刀轨，如图4(c)所示，再取行距为4生成刀轨。所有刀轨信息如表1所示，对比可知，行距自适应刀轨比行距为4.14和4的刀轨总长度分别减少了14.4%和16.1%，验证了算法的可行性和有效性。

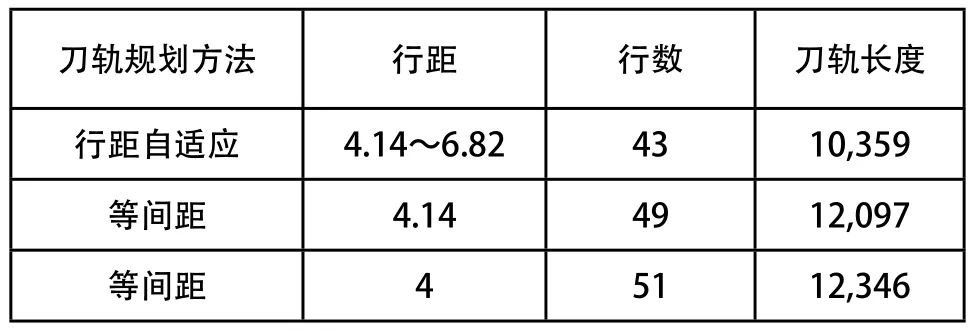
表1 生成的刀轨信息

图4 本文算法和等间距法对点云生成刀轨

4 结论

本文提出一种行距自适应的行切刀轨生成算法，根据残留高度点和刀位点的几何关系，避免等距求交，对局部点云直接采用预设初值、迭代逼近的方式计算出残留高度点和下一行刀位点，从而获取满足残留高度的最大行距，在保证精度的前提下提高了计算效率，与等间距法相比，刀轨长度明显减小。在未来的研究中，可进一步研究提高算法效率的方法以及计算理论残留高度点和刀位点的方法。

[1]Suresh K, Yang DCH. Constant scallop-height machining of freeform surfaces[J].ASME Journal of Engineering for Industry,1994,116(2)：253-259.

[2]Zhu H, Liu ZJ, Fu JH. Spiral tool-path generation with constant scallop height for sheet metal CNC incremental forming[J].The International Journal of Advanced Manufacturing Technology,2011,54 (9-12)：911-919.

[3]石宝光,雷毅,闫光荣.曲面映射法生成等残留环切加工刀具轨迹[J].工程图学学报,2005,26(3)：12-17.

[4]陈晓兵,廖文和,吴海兵,孙全平,陈前亮.三角网格表面等残留高度刀轨生成算法[J].计算机辅助设计与图形学学报,2009,21(12)：1800-1804.

[5]原恩桃,廖文和,刘浩.细分曲面等残留高度刀轨规划[J].机械科学与技术,2009,28(9)：1143-1146.

[6]徐金亭,刘伟军,卞宏友,王华兵.基于网格曲面模型的等残留刀位轨迹生成方法[J].机械工程学报,2010,46(11)：193-198.

[7]吴福忠,华小洋,连晋毅.测量点数据等残留高度刀具路径规划[J].计算机辅助设计与图形学学报,2007,19(12)：1618-1623.

[8]吴福忠.点云曲面等残留高度刀具路径规划[J].计算机集成制造系统,2012,18(5)：965-972.

[9]Liu W, Zhou LS, AN LL. Constant scallop-height tool path generation for three-axis discrete data points machining[J].The International Journal of Advanced Manufacturing Technology,2012,63(1-4)：137-146.

[10]刘威,周来水,安鲁陵.点云模型再设计的刀轨重新生成技术研究[J].计算机集成制造系统,2013,19(10)：2432-2437.

[11]刘威.点云模型的数控加工刀轨生成关键技术研究[D].南京：南京航空航天大学,2013.