高速微铣削稳定性的声发射监测

齐 云，许金凯，于占江，于化东

（长春理工大学 精密制造及检测技术国家地方联合工程实验室，长春 130022）

0 引言

高速微铣削作为一种快速、低成本的微加工方式，由与其切削用量小、加工精度高等特点而被广泛应用于微小零件的加工。高速微铣削作为切削加工领域中应用最为广泛的技术之一，目前的研究主要集中于加工表面质量、切削力、刀具的磨损等方面，对加工过程的稳定性研究很少[1～4]。加工过程的稳定性影响着加工的表面质量，对加工过程进行实时监测，能够获知加工状态是否正常，通过对加工状态的实时评定，可以对加工参数的调整、刀具更换的时机提供参考依据。

声发射（Acoustic Emission，AE）技术作为一种成熟的监测方法，在故障诊断、刀具破损等领域被广泛应用[5,6]。文献[7]中唐英等人将声发射监测技术引入了对传统车削过程的监测，研究表明AE信号强度与切削用量、工件材料有密切关系。仲为武[8]等人在AE信号监测传统硬铣削过程试验中发现AE信号的均方根值受每齿进给量和铣削深度的影响很小，切削速度提高时AE信号的频谱成分增多。这为将声发射技术应用于高速微铣削过程监测的研究奠定了一定的基础。为了有效的提取声发射信号特征值以表征切削过程加工的稳定性，通常采用高斯滤波、小波滤波等方法对信号进行去噪处理[9,10]。滤波法理论上可以去除噪声提取信号中的有效信息，经典的高斯滤波对于正态分布的信号有较好的滤波性能，但由于实际信号有许多不可避免的随机噪声，所以高斯滤波会对处理结果产生畸变；小波滤波虽能克服传统滤波方法的缺陷，但其分解次数和小波基的确定受使用者经验的影响，制约了这种方法的发展。经验模态分解法[11]（Empirical Mode Decomposition，EMD）作为一种完全基于信号自身频率特征的分解方法，在处理非稳态非周期信号时被广泛应用。由于此分解方法易产生模态混叠的问题，Huang[12]提出了添加高斯白噪声的集合经验模态分解法（Ensemble Empirical Mode Decomposition，EEMD）对信号进行去噪，该方法通过对原始信号多次加入不同的白噪声再进行EMD分解以改变信号极值点的分布来抑制模态混叠。

因此，本文采用声发射技术，对7075铝合金进行高速微铣削试验，利用添加高斯白噪声的集合经验模态分解法对信号进行去噪。通过对信号特征值的提取和计算来衡量切削过程的稳定性，为高速微铣削过程监测提供依据。

1 声发射技术监测高速微铣削加工过程试验

1.1 试验方法

选取4个微铣削加工参数：主轴转速n（r/min），进给速度vf（mm/min），轴向切深ap（μm），径向切深ae（μm）进行4因素2水平全因子试验。试验参数如表1所示。

1.2 试验材料与设备

试验材料为预先加工出长方体凸台的直径为20mm的7075铝合金棒料，棒体部位夹装在机床的圆形卡盘上，长方体凸台的尺寸为25mm×16mm×16mm。

表1 试验参数

图1为微铣削试验装置及流程图，试验机床为：WILLEMIN 408S2五轴立式加工中心，微铣刀直径为1mm，切削刃圆弧半径为3μm。声发射传感器固定在凸台的矩形截面上，微铣削的加工表面为凸台的正方形截面。AE信号采集的主要装置采用美国物理声学公司（Physical Acoustics Corporation，PAC）的2通道PCI-2声发射系统，配用NANO-30型声发射传感器，其中采集卡采样频率为2MHz。

图1 试验设备及信号采集流程

2 AE信号的去噪

利用EEMD对声发射信号进行分解，是基于EMD分解法的基础上[11,12]。对信号进行EMD分解，会得到一系列频率由高到低排列的本征模态分量（Intrinsic Mode Function，IMF）。每个本征模态分量满足EMD算法的分解要求。EEMD是在EMD算法之前对原始信号多次添加幅度不同的高斯白噪声，利用高斯白噪声的频率具有均匀分布统计的特性，来改变原始信号中信号极值点的分布，从而抑制模态混叠现象。

EEMD算法流程如下：

1）通过给原始信号y(t)叠加一组高斯白噪声信号w(t)获得总体信号Y(t)。

2）对Y(t)进行EMD分解，得到M个IMF分量：

3）给Y(t)每次加入不同的白噪wi(t)，i=1,2,…,n，重复步骤1）和2）此时：

4）将不同白噪声下同一阶数的IMF分量取平均值以消除白噪声带来的影响：

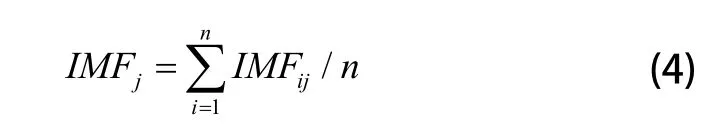
为了验证EEMD分解抑制模态混叠的效果，对分解出的IMF分量进行希尔伯特黄变换（Hilbert-Huang Transform, HHT）。希尔伯特黄变换可以对每个IMF分量计算瞬时频率，获得每个IMF分量的时间-频率图。通过时频图可以观察到每个IMF分量中有哪些频率，这些频率是如何随时间变化的。如图2所示为AE信号某两个IMF分量经HHT变换后的时频图。图2(a)中IMF分量的瞬时频率随时间的增加呈散点分布，有较多高频成分存在，频段非常宽。从图2(b)中可以看到随着加工时间的变化，该IMF分量的频率在0kHz到100kHz的范围内呈周期性变化。

图2 IMF分量的时频图

不同IMF分量的主频段不同，主频段的频率成分通常具有较大的幅值，并且频率集中。而出现模态混叠现象的两个IMF分量之间，会出现主频段重叠的现象。利用希尔伯特黄变化得到的时频信息，可以绘制IMF分量的频率-幅度图。从频率-幅度图上可以观察到IMF分量有无模态混叠现象。由于EEMD分解是一种自适应的分解方法，根据信号的总长度和算法终止阈值的选择，EEMD会分解出数量过多的本征模态分量。为了突出声发射信号的特点，减少数据的运算量，对EEMD分解出来的M个本征模态分量进行分解能量的权重计算，选取权重最大的三个分量作为主分量，对这三个主分量分别绘制频率-幅度图如图3所示。可以清楚的看到三个IMF分量的主频集中且突出，并且没有重叠现象，所以EEMD分解法能够有效模态混叠，并用于分析声发射信号。

图3 权重前三的IMF分量的频率-幅度图

将权重前三的IMF分量作为主分量和代表信号变化趋势的残差相加，重构成去噪后的声发射信号。原始信号和去噪信号的对比图如图4所示，可以看到信号的规律特征被突出，随机信号被抑制。

图4 原始信号和经EEMD去噪的信号对比

信号数据处理流程图如图5所示。

3 试验结果

3.1 特征值计算

图5 数据处理流程示意图

试验获得的16组AE信号按照图5所示的处理流程进行去噪处理，获得的16组去噪信号如图6所示。EEMD分解重构后，对所得的去噪信号进行信号幅值、信号能量、信号中心频率三个参数的均方根、方差计算。在计算出的这6种特征值中。以信号幅值的均方根这一特征值为例，以数值最低者作为1，数值最高者作为16，将16个幅值均方根特征值保持原数值比例转为1到16这个标尺中来衡量，对所有特征值都进行如下转换。均方根计算公式见式(5)，方差公式见式(6)。M为序列X的均值。

均方根：

方差：

将每组试验转换后的特征值相加，因为方差数值更能够体现数据的波动性，尤其是幅度方差和能量方差，所以将这两个方差值的权重设为2，中心频率方差权重设为1.5，三个均方根特征值的权重为1。计算每组试验的总得分后将总得分也转换成1到16的比例尺中以方便对比和分析，用总得分来衡量声发射信号的稳定程度。16组试验对应的参数和总得分如表2所示。

3.2 结果分析

利用试验设计（DOE）的方法对试验结果进行分析。结果如表3所示。

图6 16组AE信号去噪后的时域图

表2 试验参数及对应得分

表3 试验结果分析表

从表3中结果可以看出，主模型的P值代表着模型的显著度，当P值小于0.05时说明主模型是有效的。4个参数中轴向切深的显著度小于0.05，则说明这一参数对声发射信号的稳定性的影响是最明显的。

同时根据试验结果得出回归方程：

R1是总得分，ABCD四个参数分别于表3中的编号一一对应。R1值越大，代表着声发射信号的不稳定度增加。其中只有A，即主轴转速这一加工参数与声发射信号的稳定度呈负相关。当主轴转速升高其他三个参数不变时，声发射信号的稳定度会更好，但影响的程度很小。进给速度、轴向切深、径向切深这三个参数增大时，声发射信号的不稳定度会显著增大。图7所示为外学生化后的残差的正态分布图，每一个方格代表一次试验，分布点越接近一条直线说明回归方程的拟合效果越好，从图7中可以看出此次拟合出的方程(7)较好。

图7 残差正态分布图

【】【】

根据高速切削理论，当主轴转速增大时，切削速度提高，使得金属流动速度大于塑性变形速度，同时切削温度提高，导致切削力下降。切削力的下降使得切削过程较主轴转速低时更稳定，所以主轴转速与声发射信号的稳定度呈负相关。

AE信号的主要来源是第一变形区材料的剪切变形、第二变形区切屑与工件或切削刃的接触、第三变形区工件和刀具间的摩擦。当进给速度、轴向切深、径向切深值增大时，增大了单位时间内产生的切屑体积，使得发出的声发射信号能量增大。同时单位时间内切削量的增加使得切削力增大，为切削过程引入了更多频率成分，例如刀具的震颤增加，机床的振动增加等，这些频率成分的引入使得声发射信号的波动变大，在式(7)中就表现为声发射信号的不稳定度增大。

4 结论

1）EEMD分解能够有效抑制模态混叠，适用于声发射信号的去噪和分析。

2）高速微铣削过程的稳定性可以用声发射信号的稳定性来衡量。加工参数的改变与声发射信号的稳定性密切相关。其中主轴转速和声发射信号稳定呈负相关，进给速度、轴向切深、径向切深和声发射信号稳定性呈正相关。

3）根据监测结果，为了获得更好的高速微铣削表面质量，应该采用较小的切削量，尤其是轴向切深量并提高主轴转速。

4）利用加工过程中不断采集到的声发射信号计算此时声发射信号的稳定度，能够监测切削过程是否处于正常状态。

[1]Wyen C F, Jaeger D, Wegener K. Influence of cutting edge radius on surface integrity and burr formation in milling titanium[J].The International Journal of Advanced Manufacturing Technology,2013,67(1-4)：589-599.

[2]Rahman M, Kumar A S,Prakash J R S. Micro milling of pure copper[J].Journal of Materials Processing Technology,2001,116(1)：39-43.

[3]Heaney P J,Sumant A V,Torres C D,et al.Diamond coatings for micro end mills：enabling the dry machining of aluminum at the micro-scale[J].Diamond and Related Materials,2008,17(3)：223-233.

[4]Kang I S, Kim J S, Kim J H, et al. A mechanistic model of cutting force in the micro end milling process[J].Journal of Materials Processing Technology,2007,187：250-255.

[5]袁俊,沈功田,吴占稳,等.轴承故障诊断中的声发射检测技术[J].无损检测,2011,33(4)：5-11.

[6]Tansel I, Trujillo M, Nedbouyan A,et al. Micro-end-milling—III. Wear estimation and tool breakage detection using acoustic emission signals[J].International Journal of Machine Tools and Manufacture,1998,38(12)：1449-1466.

[7]唐英,顾崇衔.金属切削过程声发射机理[J].北京科技大学学报,1995,17(5)：439-443.

[8]仲为武,王希.模具钢硬铣削过程振动和声发射信号的监测与分析[J].2015.

[9]粱敏,马凯.基于高斯滤波的回波信号去噪方法的研究[J].测绘与空间地理信息,2017,40(1)：40-42.

[10]杨杰.声发射信号处理与分析技术的研究[D].长春：吉林大学,2005.

[11]Huang N E, Wu M L C, Long S R, et al. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis[A].Proceedings of the royal society of london a： Mathematical,physical and engineering sciences[C].The Royal Society,2003,459(2037)：2317-2345.

[12]Wu Z, Huang N E.Ensemble empirical mode decomposition：a noise-assisted data analysis method[J].Advances in adaptive data analysis,2009,1(01)：1-41.