混联机器人空间插值迭代补偿法研究

郭瑞峰，彭战奎，张文辉

（西安建筑科技大学 机电工程学院，西安 710055）

0 引言

随着离线编程技术的应用与发展，在机器人离线编程技术实用化的过程中，误差补偿成了关键技术之一[1]。软件补偿法是利用机器人控制系统改变输入变量来实现误差补偿的方法，该方法成本低，操作性强，是目前常用的补偿方法。

关于机器人软件补偿的国内外研究比较多。Z. S.Roth[2]等系统地提出了通过标定的方法来提高机器人的精度。蔡鹤皋[3]等运用修正的D-H模型推导了RMA-I型机器人的实际连杆几何参数识别公式，标定后[4～6]机器人的精度能提高一个数量级。Wang[7]等运用视觉测量系统，结合神经网络算法完成了机器人非模型误差补偿。周炜[8]等提出了基于机器人误差空间网格插值的补偿方法。空间网格插值补偿法[9]是随着计算机的发展而被提出的一种新型误差补偿方法，该方法需要占用一定的存储资源，数据量比较大，补偿精度与误差数据的密度、准确度以及插值函数有关。

本文参考周炜等提出的空间网格插值补偿法，综合考虑混联机器人静态误差与动态误差因素对其定位精度的影响；在空间网格插值补偿法的基础上，提出空间网格插值迭代补偿法，通过最大允许误差控制迭代次数来得到不同的定位精度；最后通过MATLAB仿真验证了所提方法的有效性。

1 机器人工作空间分析

新型四自由度混联机器人[10]总体结构示意图如图1所示。实际加工要求如下：各连杆加工精度等级ITi=9，根据机器人各连杆理论值结合公差标准GB/T 1800.3-1998以及平行度标准GB/T 1184-1996（其中相邻关节轴线的平行度误差βi，分别由连杆l4，l5的加工精度确定），得到各连杆名义值和偏差值如表1所示。

考虑到传统DH[11]模型忽略关节轴线的微小偏角对机器人定位精度的影响，为了避免机构出现奇异性[9]，本文采用5参数的MDH模型[10,11]建立机器人运动学模型；然后选取机器人关节变量θ1，θ2以及θ3的所有排列组合值，带入建立的运动学方程中，可以得到机器人的整个工作空间，如图2所示。为便于观察，图2中只显示了θ1∈(0,270°)时机器人工作空间。

表1 新型混联机器人连杆名义值和偏差值（单位：mm）

图1 新型混联机器人总体结构示意图

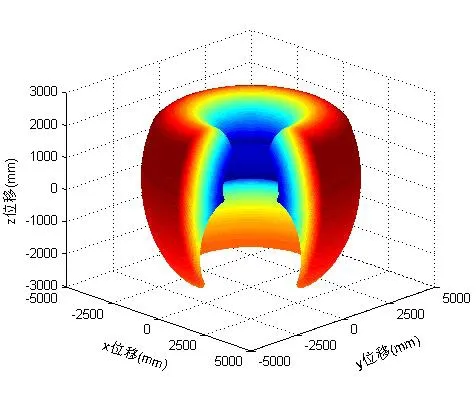
图2 θ1∈((0°，270°)时的机器人工作空间

2 误差分析

2.1 静态误差分析

由静态误差因素引起的机器人定位误差称为静态误差，静态误差因素主要有各连杆加工误差和电机跟随误差。各连杆加工误差如表1所示，三个驱动电机的最大跟随误差均为0.01°。

无需通过微分计算，将各定位点实际位置与理论位置坐标Hj0(j=x,y,z)相减，即可得到机器人定位误差在j轴方向上的分量ΔPj为：

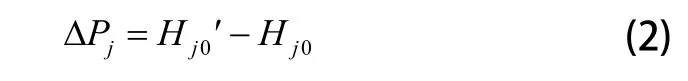
其中：Hj0（理论位置坐标在各轴的分量）为θi和的函数。

由矢量和定理，机器人的绝对静态误差ΔP为：

综上，将各连杆名义值及偏差值带入正运动学方程可以得到机器人在整个工作空间内各定位点的实际位置P′；然后将各定位点实际位置与理论位置坐标相减即可得到对应工作点各轴方向上的静态误差ΔPj。通过MATLAB编程分别以变量X，Y，Z为横坐标、纵坐标和竖坐标，机器人的绝对静态误差ΔP作为第四维颜色坐标，绘制得到机器人在整个工作空间内的静态误差云图如图3所示。

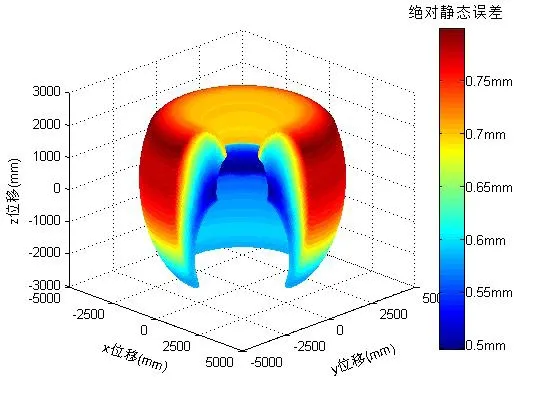
图3 θ1∈(0，270°)时的静态误差云图

2.2 动态误差分析

在动态误差分析时，为简化模型提高分析效率，将具有互换性的末端执行器及变形量很小的底座、回转平台和支座作为刚体，对其他连杆进行柔性化处理；考虑到机器人工作空间的对称性，只需仿真计算机器人在某一个竖直平面内的动态误差，其他竖直平面内的动态误差可以通过计算得到。通过LMS Virtual.lab Motion软件进行动态静力学仿真分析，可以得到机器人在o-xz正半平面上各定位点的实际位置P′。将各定位点实际位置与理论位置坐标相减即可得到对应工作点处的动态误差，然后由矢量和定理，得到机器人的绝对动态误差云图如图4所示。

从图4中可以看出，当载荷为80kg时，机器人在o-xz正半平面上动态误差的最大值主要集中在两个区域：左上角区域和右下角区域。在实际工作中，可以将这两个区域设为非工作区域。

山东省东营市东营区是吕剧的发祥地，一代又一代艺人不断致力于吕剧的传承、弘扬。雅俗共赏的吕剧已成为东营人田间地头、堂前屋后、广场剧场演唱的一门群众艺术。在现代多元文化的影响下，随着一些老艺人相继去世，40岁以下年轻人群体渐不知吕剧为何物。因此，有必要对国家级非物质文化遗产吕剧文化的发展壮大，对吕剧在实施“黄蓝”国家战略背景下发挥其作用，促进产业转型升级等进行思考和研究探讨。

分析机器人的对称结构可知，在竖直方向载荷的作用下，机器人连杆变形量与的取值无关。因此只需要根据机器人在o-xz正半平面上的动态误差数据，通过数学关系推导，即可得到机器人在整个工作空间内的动态误差。具体的推导过程如下：

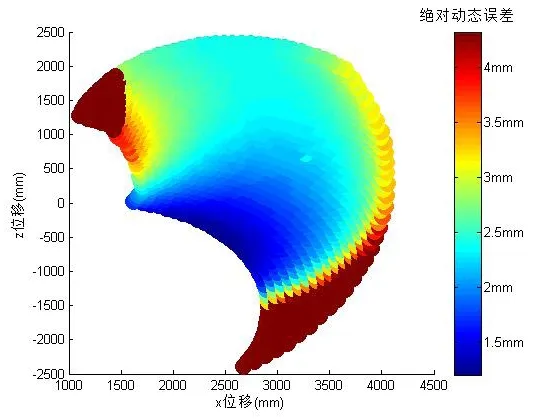
图4 G=80kg时，机器人在o-xz平面内的动态误差云图

由齐次变换法可知，考虑连杆弹性变形时，机器人在整个工作空间内的实际定位点可以表示为：

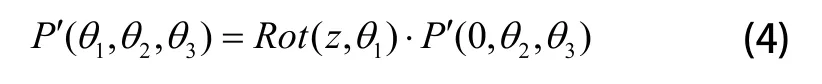
机器人在整个工作空间内的动态误差为：

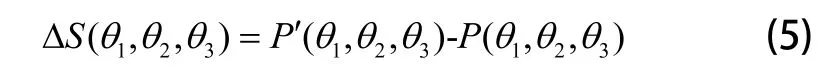
结合式(4)与式(5)，可得：

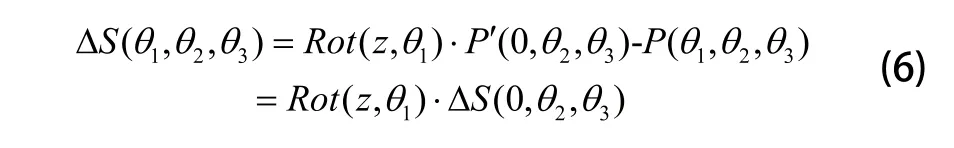
在MATLAB中编程计算得到载荷为80kg时，机器人在整个工作空间内的动态误差云图如图5所示。

比较图3与图5可知，动态误差因素对机器人末端执行器位置精度的影响程度远大于静态误差因素。且负载这一可变因素对机器人末端执行器所受广义力造成的影响，明显的引起了各连杆弹性力的变化。

2.3 误差综合

机器人静态误差是由连杆加工误差引起，属于刚体运动学误差范畴；动态误差是由连杆弹性变形引起，属于柔性体静力学误差范畴；两个过程相对独立，由误差独立作用原则，静态误差和动态误差可以进行线性叠加。由此可得机器人综合误差表达式为：

图5 G=80kg时，机器人在整个工作空间内的动态误差云图

由于静态误差分析和动态误差分析是两个相对独立的过程，因此需要将机器人静态误差数据和动态误差数据分别存储，分别进行插值计算以获得整个工作空间内任意点的综合定位误差。结合数据库原理，以数据库形式对机器人静态误差和动态误差进行存储。

由于机器人的实际工作空间是连续的，因此还需要对误差数据进行插值计算，以得到整个工作空间内连续点的定位误差。

3 空间插值迭代补偿法

3.1 空间网格插值补偿法

空间网格插值补偿法以机器人整个工作空间内离散定位点的点位误差数据为基础，通过空间网格插值的方式对机器人期望定位点的定位误差进行预测，并将预测的误差值逆补偿到理论坐标上，以提高机器人的定位精度。该方法简单，适用范围广，可进行实时补偿。

以机器人整个工作空间内的离散点为关键点进行四面体网格划分，其中空间相邻的八个点组成一个四面体，划分后的空间效果如图6所示（只显示了局部图形）。

图6 机器人工作空间网格划分局部示意图

本文采用反距离加权法[9]以两点之间距离的倒数作为权值，是一种加权平均算法。该方法以小四面体网格为最小单元，可以预测出网格内任意点P(X,Y,Z)处的定位误差，步骤如下：

1）假设四面体网格8个顶点Ki(i=1,2,…,8)的坐标为对应的定位误差为计算P点与四面体网格各顶点的距离di，根据距离反求各顶点的权值qi如下：

2）根据第一步所求权值qi，在三个坐标轴方向上分别进行加权平均计算，可以得到机器人在(,,)PXYZ处沿三个坐标轴方向上的定位误差预测值为：

由于不同定位点处的机器人定位误差不同，且在整个工作空间内机器人定位误差呈非线性分布，采用修正后的关节驱动角驱动机器人并不能使补偿后的机器人末端位置与期望的位置完全重合，仅能使其逼近期望位置，提高机器人定位精度。

考虑到空间网格插值补偿法能使机器人末端执行器逼近期望位置，而不能完全与期望位置重合，提出空间网格插值迭代补偿法，这种方法以空间网格插值补偿法为基础，通过增加补偿次数来进一步提高机器人的定位精度。

3.2 迭代补偿原理

图7 空间网格插值迭代补偿法流程图

本文按照图7所示的流程图对新型混联机器人进行定位误差补偿。以机器人静态和动态误差数据库为基础，通过空间网格插值计算机器人在工作空间内任意点处的综合定位误差，然后判断实际定位点与期望定位点之间的误差，如果误差大于设定值，则将误差值再次逆补偿到理论位置坐标上；如此反复，直至定位误差小于或者等于设定值。最后通过逆解方程得到修正后的各关节角，并用其驱动机器人。

3.3 定位误差补偿仿真试验

对新型混联机器人进行定位误差补偿仿真试验，设计试验条件如下：新型混联机器人的连杆加工误差为最大偏差值，具体数据如表1所示，三个驱动电机的最大跟随误差为0.01°，末端载荷为80kg，补偿后最大允许定位误差为0.1mm。在工作空间内任意选取10个位置点，进行MATLAB仿真得到计算结果如图8所示。

从图8中可以看出，通过迭代补偿后机器人绝对定位误差减小到0.1mm以内，定位精度得到了很大程度的提高，充分说明了空间插值迭代补偿法的有效性。

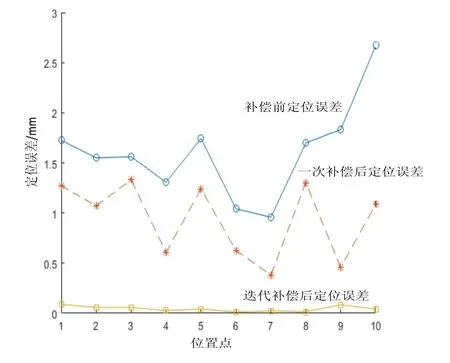
图8 补偿前后末端定位误差对比

4 结论

为提高混联机器人的定位精度，本文综合考虑静态误差中运动学参数误差与动态误差中连杆柔性误差对混联机器人在整个工作空间内定位精度的影响；对误差补偿方法进行研究，提出一种空间插值迭代补偿法，通过最大允许误差控制迭代次数可以得到不同的定位精度，用以满足不同的定位精度要求；最后通过定位误差补偿仿真试验将此算法应用到新型混联机器人定位误差补偿当中，并与空间网格插值补偿法进行对比，验证了所提方法的有效性。

[1]赵东波,熊有伦.机器人离线编程系统的研究[J].机器人,1997,(04)：75-81.

[2]Roth Z S,Mooring B W, Ravani B. An overview of robot calibration[J].IEEE Journal on Robotics and Automation,1987,3(5)：377-385.

[3]蔡鹤皋,张超群,吴伟国.机器人实际几何参数识别与仿真[J].中国机械工程,1998,(10)：17-20.

[4]宋月娥,吴林,田劲松,等.用于机器人离线编程的工件标定算法研究[J].哈尔滨工业大学学报,2002,(06)：735-738.

[5]王鲁平.串联机器人多误差因素影响下定位精度分析及其误差补偿[D].合肥工业大学,2015.

[6]Verdonck, Walter. Experimental robot and payload identification with application to dynamic trajectory compensation[J].Production Engineering Machine Design & Automation,2004.

[7]Wang D, Bai Y, Zhao J. Robot manipulator calibration using neural network and a camera-based measurement system[J].Transactions of the Institute of Measurement and Control,2012,34(1)：105-121.

[8]周炜,廖文和,田威.基于空间插值的工业机器人精度补偿方法理论与试验[J].机械工程学报,2013,(03)：42-48.

[9]陈宵燕,张秋菊,孙沂琳,等.工业机器人位姿误差空间IDSW插值补偿方法研究[J].机械科学与技术,2017,(03)：378-385.

[10]郭瑞峰,彭光宇,杨柳,等.基于MDH模型的新型混联码垛机器人运动学分析与仿真[J].机械传动,2017,(02)：122-127+138.

[11]戚祯祥,叶超强,吴建华,等.基于MDH模型的工业机器人标定算法与实验研究[J].制造业自动化,2015,(4)：15-17,26.