基于小子样的武器装备维修性评估方法

施亚洲，李文强，李 彦

（四川大学 制造科学与工程学院，成都 610065）

0 引言

维修性是指在规定的时间内与规定的条件下，按规定的方法和程序进行维修时，保持、恢复或改进其规定状态的能力[1]。维修性评估是指为了确定产品是否满足维修性要求所进行的试验与评定工作。为了提高产品的维修性水平，一方面需要在装备研制阶段提高武器装备维修性设计水平，另一方面需要在新研制武器装备的定型、试用阶段考察其维修性水平，需对其进行维修性评估，并作为武器装备试验与鉴定验收的重要依据之一。

现阶段维修性评估方法主要有两种：一种是按GJB2072-94《维修性试验与评定》中所提出的维修性评估方法[2]，这种方法是在较大样本的前提下进行的，但多数情况下，因经费、条件等因素的限制，获取很多的现场数据和进行大量的维修性试验是很困难或不现实的，而且，研制过程中大量的维修信息未得到有效的利用。另一种方法是在试验中利用小子样试验方法减少对试验样本量的依赖程度，达到缩减试验样本的目的[3～7]，这种方法一般都是针对单一指标的评估，评估结果具有一定的片面性。本文基于上述两个问题，结合了Bayes统计理论与灰色聚类评估理论实现了在小子样条件下多维修性指标的综合评估。

1 样本的Bayes统计过程

1.1 武器装备维修性指标

武器装备的维修性指标一般是通过维修时间或维修工时来描述的。通常包括以下几个指标：平均维修时间（Mean time to repair，MTTR）、装备维修时间中值、装备最大修复时间等，本文选取这三个指标进行综合评估。

1.2 维修时间总体分布类型的确定

维修时间采用对数正态分布的假设在大多数情况下是合理的[2]。本文在对维修时间总体分布有效性检验时采用K-S检验方法。步骤为：

1）构造分布函数：

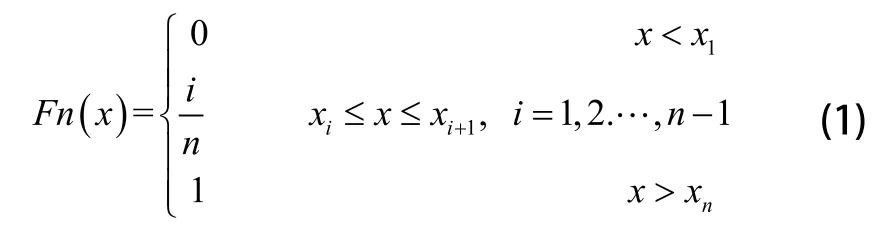
其中，x为样本数据，n为样本总数。

2）计算最大偏差Dn值：

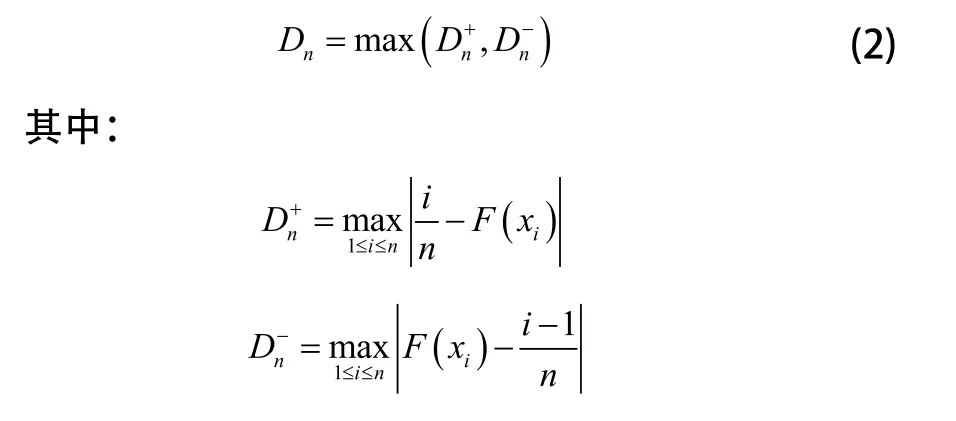
3）通过K-S检验临界值表查得临界值Dnα，若Dnα＞Dn则总体样本服从对数正态分布，否则，不服从。

1.3 先验分布的确定

本文采用的先验信息主要是历史试验数据，历史试验数据是指在装备研制和其它性能试验过程中得到的维修性数据。在利用历史试验数据确定先验分布之前需对历史试验数据进行转换，不能将历史数据与现场试验数据等同看待，例如某武器装备出现了故障，对处于武器装备研制阶段的维修时间和处于该装备装配完成后定型试验阶段的维修时间，其检测、拆卸、调整等时间都有较大差别，不能直接使用。为了利用历史试验数据需要将验前数据信息转化为现场试验条件下（即同一阶段）的数据信息。其转换过程如下：

设维修时间要素的集合T=(t1，t2，…，tn)T，其中ti(i=1,2,…,n)表示检测时间、拆卸时间、更换时间、重新组装时间、调整时间和检查时间等。则维修时间x为：

x'为：

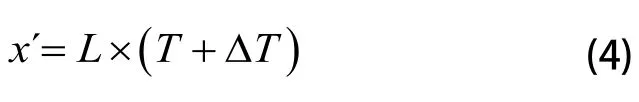
当样本服从对数正态分布时，需要确定正态分布未知参数，目前，在小字样条件下确定先验分布未知参数的方法主要有两种：自助法[8～10]和随机加权法[11,12]。由于随机加权法比自助法的数据跳跃性大，数据的区域也较长，更能反映装备维修时间的实际分布情况，而且，随机加权法较自助法具有较高的精确度[13]。因此，文章利用随机加权法来计算先验分布。

设Xn=(x1，x2，…，xn)T为历史数据中维修时间转换后的样本数据，且服从对数正态分布，为了确定先验分布密度即确实其先验分布的期望值μ和方差σ2，其过程如下：

1）通过下式计算出样本的均值和方差。

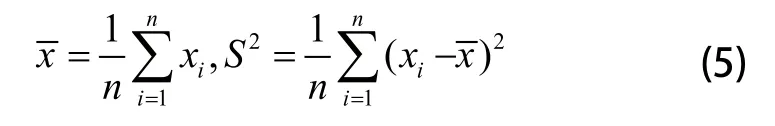
2）产生N组服从Diricklet分布D（1,1，…，1）的随机向量其中，i=1,2,…,N。设联合分布为：为了得到联合分布，首先产生n-1个服从U(0，1)的独立同分布序列v(1)，v(2)，…，v（n-1），按由小到大的次序重新进行排序，记v(1)＜v(2)…＜v(n-1)。令v(0)=0，v(n)=1，则的联合分布就是

4）分布参数μ、σ2的估计值可通过下面公式进行计算：

其中N可以为任意大的自然数。

1.4 维修性验后分布的计算

设θ为平均维修时间，θ0为平均维修时间的最大可接受值。X为平均维修时间的样本值，且X服从对数正态分布，即则：

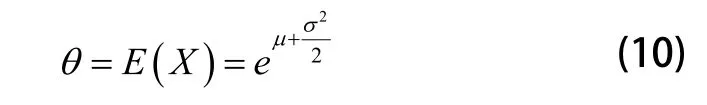
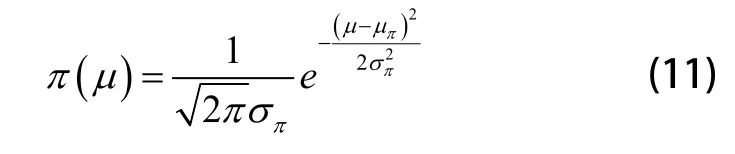
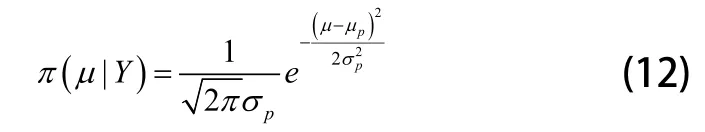
其中：

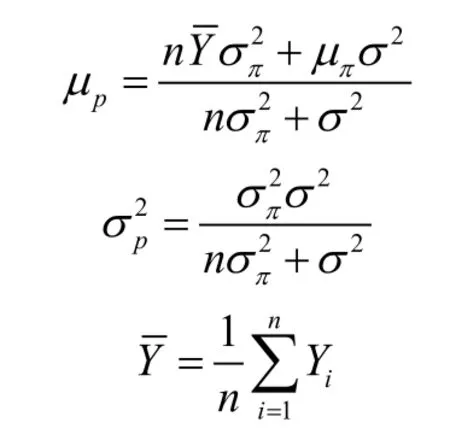
2 灰色聚类评估过程

2.1 维修性指标的点估计与区间估计

2.1.1 维修性指标的点估计

1）平均修复时间

平均修复时间为维修时间分布的数学期望值。即为：

2）最大维修时间（Mmax）

最大维修时间是指在一定维修度下维修时间的最大值。即为：

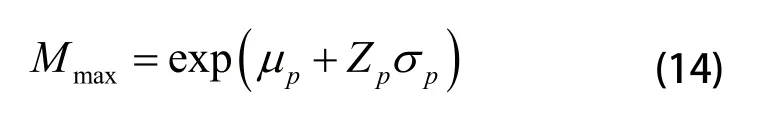
其中，Zp为维修度为p时的正态分布分位点。

3）维修时间中值（Mmid）

维修时间中值是指维修度为50%是的维修时间值。即为：

2.1.2 维修性指标的区间估计

平均维修时间的区间估计：

置信上线为：

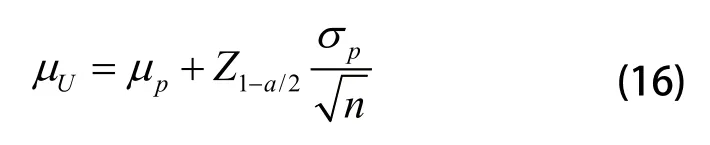
其置信下线为：

其中：Za/2为正态分布的a/2分位点，可查表得，n为样本总数。

最大维修时间和维修时间中值可根据式(14)～式(17)求得。

2.2 指标权值的确定

1）根据表1标准构造判断矩阵A

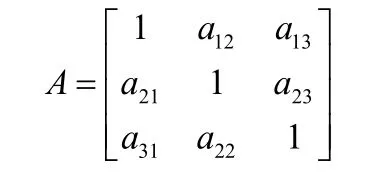
表1 判断矩阵元素取值标准

2）权值计算

归一矩阵列矢量：

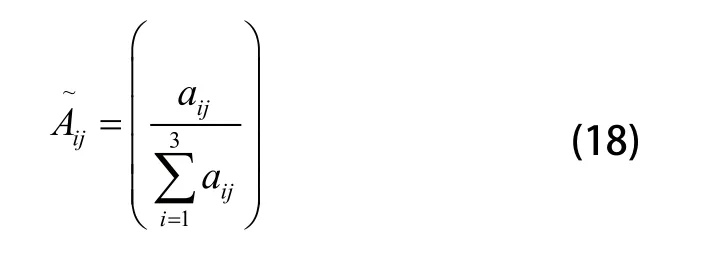
对式(18)，计算按行的相对权值：

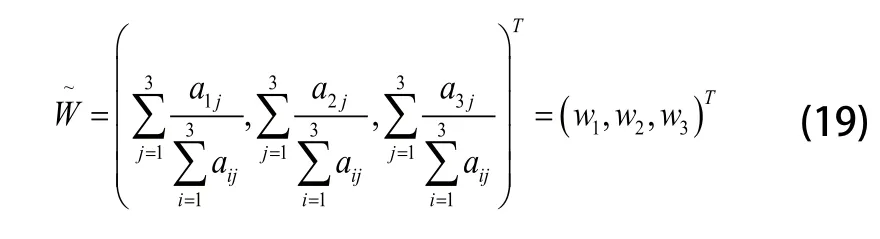
对wi进行归一化处理：

权值矢量为：

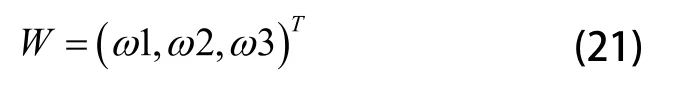
矩阵的最大特征根值为：

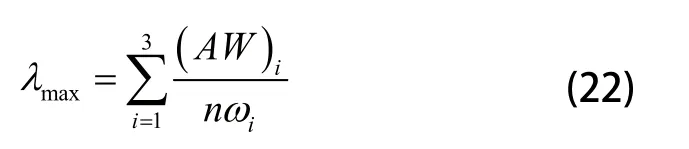
3）一致性判断

通过下式计算CI：

计算CR值：

若CR＜0.1，这判断矩阵可以接受，权重比较合理。

2.3 维修性可拓区间的计算

根据武器装备实际工程需要，维修性从高到低分为以下四个等级：第一类：“优”，第二类：“良”，第三类：“中”，第四类：“差”。若维修时间样本数据最大值、最小值分别为为xl、xs，指标估计区间为：[al,as]。

则聚类分界点为：

其中：aM为指标估计区间的中值，xM为样本最大值与最小值的中值。

则四个等级对应的灰类区间为：

“优”：0～b1；“良”：b1～b2；“中”：b2～b3；“差”：b3～∞。

2.4 维修性指标聚类评估矩阵的建立

令第一类的上限为E，第二类的中限为G，第三类的中值为M，第四类的下限为P，第i个指标对应的白化数据为di。

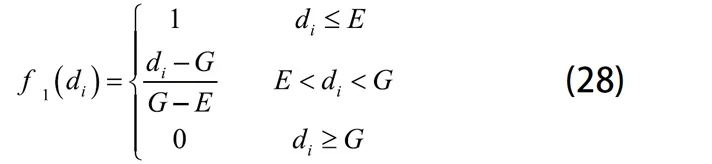
第二类，di∈[E,M)，计算如下：

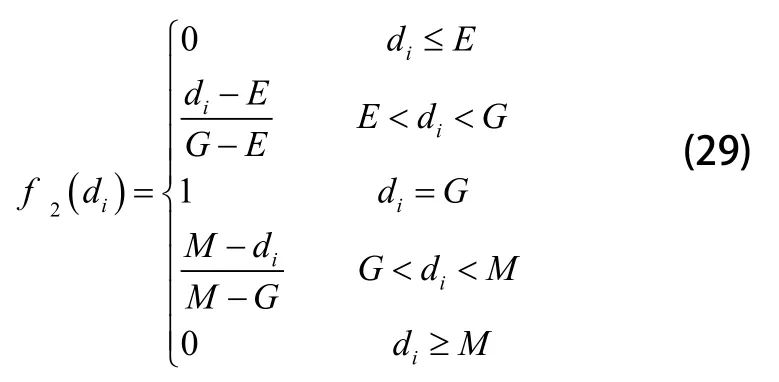
第三类，di∈[G,P)，计算如下：

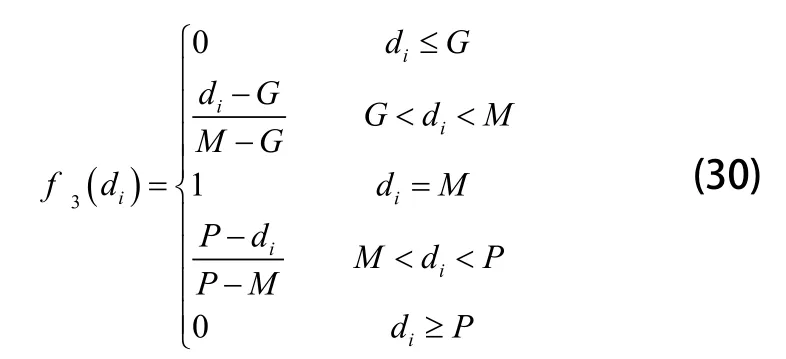
第四类，di∈[M,∞)，计算如下：

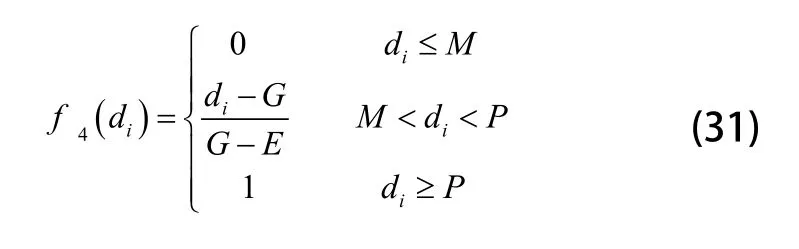
将通过式(13)～式(15)计算的三个指标的点估计值di，其中，i=1,2,3分别代入四类白化权函数，得到一个4×3节矩阵R，且R为：

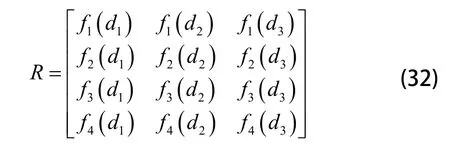
综合评估模型为：

维修性指标评估结果：

评估灰类为“优”、“良”、“中”、和“差”4类，则将这4个灰类对应的评估灰值定为：C={1 0.8 0.6 0.4}。

最后的评估值Q为：

按表2确定维修性水平等级。

表2 维修性聚类表

3 实例分析

某武器装备的历史维修时间、现场试验数据如表3所示。

表3 维修时间数据表

3.1 维修时间分布的确定

根据1.2节K-S检验法计算得Dn=0.23，查表Dnα=0.48，因Dnα＞Dn，则该样本数据符合对数正态分布。通过1.3节计算其先验分布为N（1.3462，0.354），由式(12)可等μp=1.7254，σp=0.4372。

3.2 维修性指标点估计与区间估计值

由式(13)～式(17)，可求得平均维修时间，最大维修时间，维修时间中值的点估计和区间估计如表4所示。

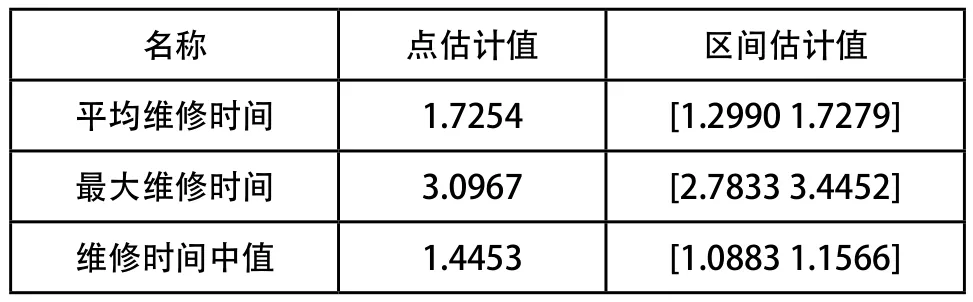
表4 维修性指标的估计值表

3.3 灰色聚类评估过程

1）指标权重的确定

根据表1建立平均维修时间、最大维修时间、维修时间中值的权重判断矩阵如下：

由式(16)～式(18)，可得：ω1=0.648，ω2=0.23，ω3=0.122，且CR=0.004＜0.1，判断矩阵通过一致性检验。三个指标的权重向量W=（0.648 0.23 0.122）T。

2）可拓区间的确定

由式(25)～式(27)可得三个维修性指标的可拓区间，如表5所示。

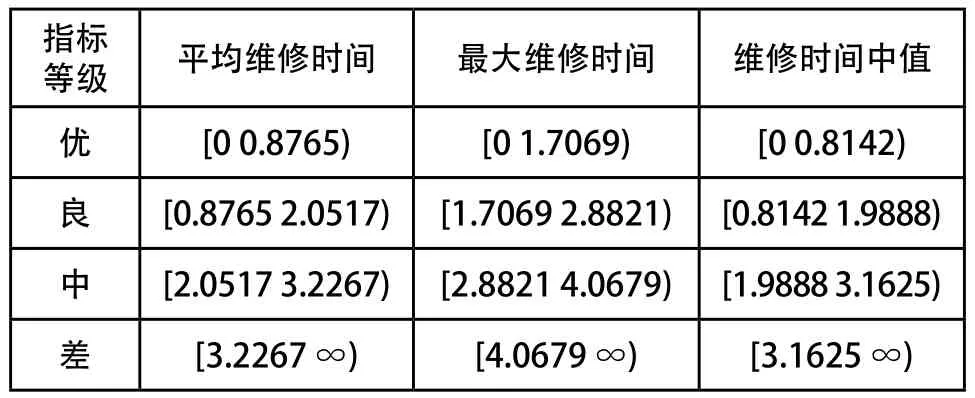
表5 维修性指标的可拓区间

3）综合评估矩阵的计算

由表5可得平均维修时间的第一类上限值：0.8767，第二类中限值：1.4642，第三类中限值：2.6392，第四类下限值：3.2267，则白化权函数公式如下：

（1）第一类白化权函数：

（2）第二类白化权函数：

（3）第三类白化权函数：

（4）第四类白化权函数：

将平均维修时间点估计值1.7254代入式(35)～式(38)可得向量[0 0.7777 0.2223 0]T，同理可求得最大维修时间的向量为：[0 0.3176 0.6824 0]T，平均维修时间中值的向量为：[0.972 0.028 0 0]T。则矩阵R为：

则由式(33)可得综合评估向量B为：

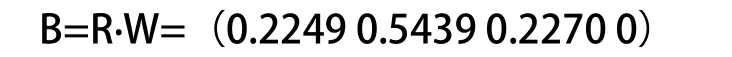
4）评估结果

由式(34)可得Q=0.794，如表2所示，可知该武器装备的维修性良好。

4 结论

本文针对维修性评估方法中的样本需求量大、试验周期长、单指标评估等问题进行了研究，通过Bayes方法有效的利用历史维修信息减少了试验样本数据量，并结合灰色聚类方法完成了维修性的综合评估。并通过实例验证了该方法的可行性及实用性，该方法能有效的减少了试验样本量，缩短了试验周期，并实现多指标的综合评估。

[1]甘茂治.维修性设计与验证[M].北京：国防工业出版社,1995：11-12.

[2]GJB 2072-94,维修性试验与评定[S].

[3]Yang J F,Zhou Y,Hou T,et al.Study on multi-information fusion modal basedon feature credibility of sensor[J].Transducer & Micro system Technologies,2013,32(2)：42-50.

[4]侯敏,郭基联,李建伟.多源信息的验前分布融合方法研究[J].火力与指挥控制,2012,37(7)：57-60.

【】【】

[5]刘勇,徐廷学,彭军.维修时间截尾序贯验后加权检验的实现[J].现代防御技术,2014,42(1)：106-110.

[6]Jiao Z,Ding X,Song G.A Study on Maintainability Test Methods for Radar Equipment[J].Modern Radar,2013.55-60.

[7]董博超,宋保维,梁庆卫.武器装备小子样维修性试验与评定方法研究[J].兵工学报,2011：110-112.

[8]Gal E.Bagged structure learning of Bayesian networks[A].14th International Conference on Artificial Intelligence andStatistics[C].2011：251-259.

[9]Li Y、Zheng S L、Jiang H X. Research on reliability assessment method based on bootstrap method[A].International Conference on Quality,Reliability,Risk,Maintenance,and Safety Engineering and the 3rd International Conference onMaintenance Engineering[C].2012：870-873.

[10]Zu X F、Liu G. Research on measurement uncertainty resampling reverse analysis based on bootstrap simulation[A].World Congress on Engineering and Te-chnology[C].2011：978-981.

[11]Niklas N G,Orre R.Case based imprecision estimates for Bayes classifiers with the Bayesian bootstrap[J]. Machine Learning,2005,58(1)：79-94.

[12]Gareth W P,Mario V W,Pavel V S.Chain ladder method：Bayesian bootstrapVersusclassical bootstrap[J].Insurance：Mathematics and Economics ,2010,47(1)：36-51.

[13]张湘平,张金槐.基于随机加权法的Bayes精度评定[J].国防科技大学学报,2001,23(3)：98-102.