基于改进型遗传算法的制造资源优化配置方法研究

高新勤，荆彦臻，杜景霏

（西安理工大学 机械与精密仪器工程学院，西安 710048）

0 引言

近年来，云制造理念的提出与快速发展，促使制造业朝着全球化、智能化的方向迈进了一步。制造资源供需双方可以充分利用云制造服务平台进行线上匹配和交易，实现“分散资源集中使用，集中资源分散服务”[1]。但随着制造资源和相关制造任务分别向着海量化和多元化的趋势发展，新的问题应运而生，即如何为制造任务发起人提供所需的制造资源配置方案，使得最终的配置结果在某一方面或多个方面达到最优。

大量学者对遗传算法求解资源配置问题进行了研究。尹胜等提出了多任务和多目标的外协加工资源优化配置模型，并运用遗传算法对模型进行求解[2]。Kundakci and Kulak针对作业车间中的工人数量、设备数量等随机动态事件，提出了运用混合遗传算法解决动态作业车间的调度问题，并通过实例加以验证[3]。袁庆霓等提出一种资源-任务关系矩阵编码方式的遗传算法，约束了制造资源间的关联性[4]。张雪艳提出了一种自适应交叉率和变异率的遗传算法，通过该方法优化了算法的运算过程[5]。总的来说，已有大多数研究对遗传算法运算过程的复杂性考虑较少。此外，云制造仍处于初期阶段，在资源优化配置的数学建模、求解算法设计等方面还存在诸多问题，需要继续改进算法以适应不断出现的各种复杂情况。

本文根据云制造的特点和目标，构建资源优化配置问题的评价函数模型。对传统遗传算法的选择、交叉和变异等过程进行改进，提高求解算法的寻优效率和收敛性。最后通过实例验证了本文所提模型和改进算法的有效性。

1 制造资源配置问题描述

云制造是云计算向制造业的延伸，它将制造服务虚拟化到云制造服务平台（简称云平台）中实现制造服务的高度集成共享和高效利用[1]。制造资源是一个广泛的概念，是指所有能在制造全生命周期中发挥作用的资源[6]。云平台是实现云制造服务的重要载体，制造资源供需双方分别通过云平台将资源上传至云端进行整合，通过智能化搜索技术进行优化匹配，从而实现“制造即服务”的要求。

随着制造业的飞速发展以及云平台的不断改善，平台资源池中的制造资源会呈现多元化和海量化的趋势。在大多数实际制造任务中不会单一地使用一种资源，而是多种资源相互组合、相互关联，共同形成一条或多条制造任务链。因此，如何按照制造任务发起人的需求对众多任务链进行优化选择成为了当前面临的一个主要难题。如一项加工齿轮的任务集，任务发起人需要在云平台中搜索各项加工任务所需的加工设备资源，并且要综合考虑任务交付时间、加工成本以及加工质量等多个目标要求。这类制造资源配置问题属于多目标优化问题，各目标之间存在无法比较或相互冲突的可能，基本上不存在所有目标都达到最优的解，同时多目标问题的结果通常用一个解集来表示，且解之间不能单纯地比较优劣。

对制造资源优化配置问题进行建模，设某制造任务包含n项分任务，用集合TaskSet表示为：

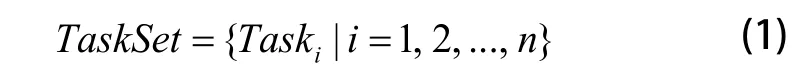
其中：Taski表示任务集的第i项分任务。

假定每项任务都需由不同的资源完成，Taski可供选择的制造资源数量为mi，它们形成制造资源集TaskMRi，即：

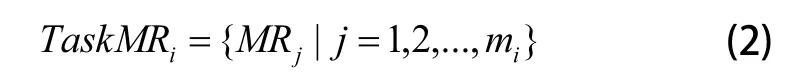
其中：MRj表示完成分任务Taski的第j个制造资源。

制造资源优化配置问题属于NP难题[7]，本文将以该问题为研究对象，构造评价函数并设计求解算法，最终获得最优的资源配置方案。

2 制造资源配置评价函数构造

根据行业调研和实际需要，设定制造资源配置问题的优化目标分别为交付时间、加工成本和加工质量。

2.1 交付时间

交付时间由加工时间和联结时间两部分构成。其中，加工时间指进行加工作业的时间；联结时间指工件由本项任务所在地运输至下一项任务所在地的时间。针对上述概念，构造交付时间的评价函数为：

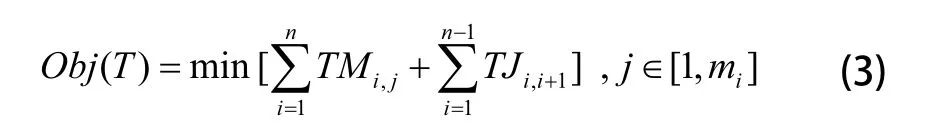
其中：TMi,j表示第i项任务的第j个资源对应的加工时间；TJi,i+1表示加工件从第i项任务所在地运送至第i+1项任务所在地的联结时间。

2.2 加工成本

加工成本包括制造资源进行直接制造活动所产生的制造成本以及将工件运输至下一任务所在地所产生的联结成本。在云模式下，制造资源分布广泛，不同区域的运费起步价位、燃油费等均存在差异，不能将运输成本同运输时间做等价处理。加工成本的评价函数构造为：

其中：TMi,j表示第i项任务的第j个资源对应的制造成本；TJi,i+1表示加工件从第i项任务所在地运送至第i+1项任务所在地的联结成本。

2.3 加工质量

加工质量指制造资源完成加工任务时在工艺、精度、规格等方面的优劣程度。云模式下，加工质量将依据资源本身的历史活动分数进行评价。历史活动分数是由以往使用过该特定资源的任务发起人对该资源在加工质量方面所做出的直观打分，并进行综合平均计算后得到的结果，数值范围为[0,1]。加工质量是新任务发起人用来选择制造资源的重要参考指标，评价函数为：

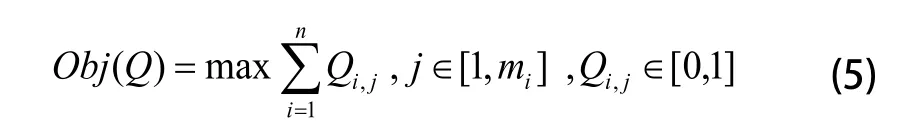
其中：Qi,j表示第i项任务的第j个制造资源对应的加工质量。

3 制造资源配置求解算法设计

遗传算法是智能算法研究领域中的热点，并且云模式下资源的优化配置与遗传算法的自然选择过程和适者生存的思想有一定的相似性[8]。传统遗传算法在解决多目标优化问题时虽然具有相对完整的求解思路和运算体系，但它没有充分利用每次迭代产生的反馈信息，造成迭代盲目、求解效率偏低等问题。虽然可以采用精英保留策略使经过选择操作后最优的个体（即染色体）不参与交叉和变异而直接保留到新种群中，并代替经过交叉、变异后的最劣个体，但该方法会在一定程度上抑制种群的多样性，易造成算法的早熟。因此，对传统遗传算法进行改进，增强算法的寻优效率和自适应性。本文将在对传统遗传算法进行充分研究的基础上，针对云模式下制造资源的优化配置问题对算法进行改进。设定算法种群规模为M，迭代次数为N，染色体长度，即基因数为n。

3.1 适应度函数设计

遗传算法在进化搜索的过程中以适应度函数为依据。本文采用权重法对评价函数中的交付时间（T）、加工成本（C）及加工质量（Q）进行整合优化，并为每项评价函数分配相应的主观权重。在实际问题中，不同类型的数据有不同的评价量纲，无法直接整合，需要对其进行标准化处理，即将不同类型的数据运用科学的数据变换方法压缩到区间[0,1]上，使其具备相互可比较性。针对该问题，采用一种实用的数据标准化处理方式，综合考虑各函数的优化目标，并将目标函数T、C和Q构造为单一目标的适应度函数F，即：

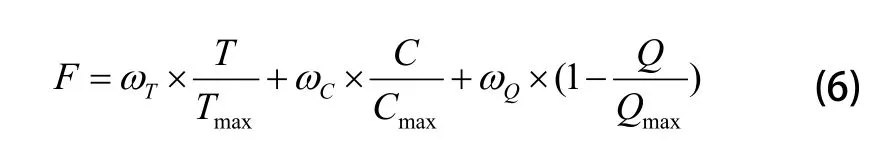
其中：ωT、ωC、ωQ表示各函数的权重系数，满足ωT+ωC+ωQ=1，将依照制造任务发起人的要求进行设定；Tmax、Cmax、Qmax分别表示任务集对应的交付时间、加工成本和加工质量的上限值。通常情况下该类数值需根据实际问题进行前期多次试算得出。

3.2 染色体编码与生成

遗传算法有多种编码方式，其中实数编码方式在基因型空间中的拓扑结构与其表现型空间中的拓扑结构一致，编码和解码操作简单，适合于解决制造资源优化配置问题。染色体X={x1,x2,...,xj,...,xn}表示任务集共由n项任务构成，基因xj表示第j项任务所选取的制造资源的编号。这种编码方式的关键在于如何保证种群中所有染色体的基因都能满足问题的约束条件[9]。结合遗传算法编程中的实际情况，提出一种基于上限约束的基因生成方法。设定上限染色体（或称上限数组）为V={v1,v2,...,vj,...,vn}，其中vj对应第j项任务的候选资源数。在运算过程中设定每个基因位的取值范围为[1，vj]，从而保证了基因生成的合法性，具体过程如图1所示。

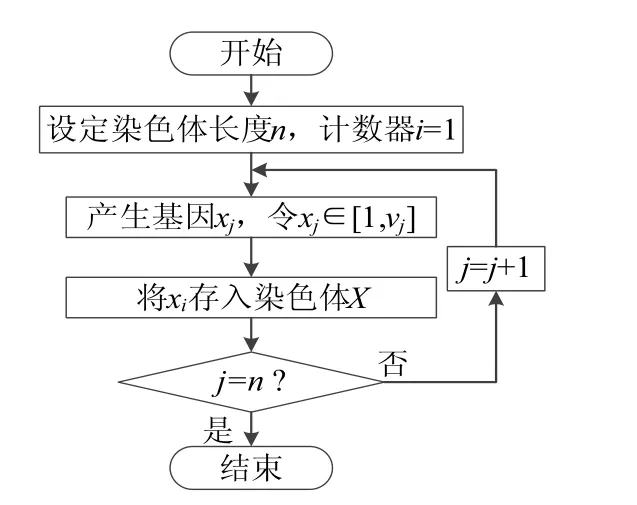
图1 染色体合法生成流程

3.3 选择

“选择”提供了遗传算法的驱动力，是遗传算法向最优解逐步迈进的主要手段。通常情况下较优的个体会在算法的选择操作后有更大的几率存留下来。比较常见的策略有轮盘赌法和锦标赛法。

1）轮盘赌法

轮盘赌法的原理是根据每个个体适应度值的比例确定该个体的选择概率或生存概率。由于本问题的适应度函数为越小越优，因此设定选择概率的计算公式为：

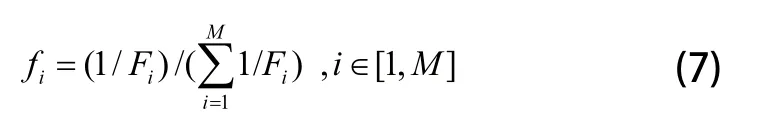
其中：fi表示个体i对应的选择概率；Fi表示个体i对应的适应度值。

适应度函数值越小，选择概率越大，表示个体的适应力越强，将会有更大的几率被选中生存下去。

选择概率计算完后，将其转换成累计概率。个体i的累计概率Pi中下限Pimin和上限Pimax的计算公式为：

当种群中的个体差异较低，即优质个体与劣质个体的适应度值偏差不大时，会影响轮盘赌法对较优个体的选取效率，不利于种群的优良化。但采用轮盘赌法进行选取操作有利于保持种群的多样性，一定程度上可以避免算法的早熟。

2）锦标赛法

锦标赛法的原理是在种群中随机抽取一定数量的个体（保证每个个体被抽中的几率是相同的），之后选择其中最优的个体放入新种群中，并重复该操作，直到产生与之前规模相当的新种群。通常情况下锦标赛法的选取结果受每次选取的个体数量Ct影响，Ct设定越大，说明每次选取过程中参与比较的个体数量越多，因而最终保留的个体相对越优良。但是，Ct越大也会使得每次选取后保留的个体趋于相同，从而破坏种群的多样性，易造成算法的早熟。

传统遗传算法多采用轮盘赌法进行选择操作，本文提出了一种基于轮盘赌法和锦标赛法的混合选取法，即在算法的交叉操作前对种群进行选取操作，使得进行交叉的父代染色体分别通过轮盘赌法和锦标赛法选取出来。该方法继承了锦标赛法在选取优良个体的高效性，又利用轮盘赌法保证了选取结果的多样性，一定程度上降低了算法早熟的风险。

3.4 交叉

“交叉”是种群进化的必要保证。通过选择操作挑选出M/2组染色体，每组染色体由两条染色体组成，记为父代。之后对每组染色体依次进行交叉判断，满足交叉条件的染色体组进行交叉操作产生临时新个体，直到种群中的所有染色体组完成交叉操作后产生临时新种群。交叉率Pc为父代交叉操作的概率，确定其取值范围比较困难，没有任何标准可遵循，且不同类型的问题有不同的选取方式[10]。在算法迭代初期阶段，为了保证个体多样性，通常选取较高的交叉率；而在迭代后期，为了保证种群趋于稳定，需要适当降低交叉率。本文采用一种线性递减函数的方式对变异率进行自适应修正。设定初始交叉率和终止交叉率分别为Pc1和PcN，计算各代交叉率Pci的公式为：

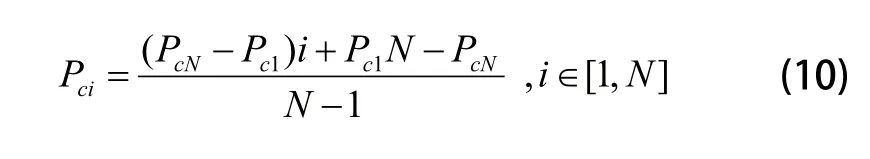
其中：i为当前代数。

为防止算法的进化过程趋于随机搜索，通常情况下可设定Pc取值范围为[0.5,0.8]。交叉操作过程如图2所示。

3.5 变异

交叉完成后将对临时新种群中的所有染色体进行变异操作，变异是实现种群多样性的重要途径，并且可以预防算法的早熟现象。由于染色体上的每一个基因位都对应不同的取值范围，因此变异过程存在基因约束。在传统遗传算法的变异操作中，染色体基因发生变异是随机和盲目的，没有任何原则可遵循，即变异不具备反馈特性，易造成算法盲目迭代、收敛速度慢等问题。本文将蚁群算法的正反馈特性引入遗传算法中，通过信息素更新原则指导遗传算法的变异规则[11]。在蚁群算法中，优质的路径会吸引更多的蚂蚁走过，从而留下更多的信息素，因此可用信息素量表示解的优质性，即信息素量越高，对应的解越优质。本文研究的问题为越小越优，因此个体适应度值越低，信息素量则越高。

图2 交叉操作流程

按照蚁群算法中信息素量决定交换变异点，确保交换后基因变异位置前后路径上的信息素量比变异前的高。随机选取某条染色体上的基因位j进行变异，对变异前后的基因位周围进行信息素量比较，公式为：

其中：Phx,y表示染色体内由基因x至基因y所产生的信息素量。

该方法不仅保护了种群迭代的多样性，同时也避免了精英保留方式对算法搜索活性造成的影响，充分提高了算法的寻优效率，优化了求解的质量。基于蚁群算法改进变异算子的流程如图3所示。

为了增强变异带来的反馈特性，通常情况下选用多基因点变异的方式，并设置较高的变异率。但变异率过高不利于算法后期的快速收敛，且运算后期优良个体的提升空间明显缩小，此时对优良个体进行变异操作只会额外增加算法的负担。为保证正反馈特性，同时优化算法收敛效果，这里提出了一种对主观变异率Pm进行修正的方法，计算公式为：

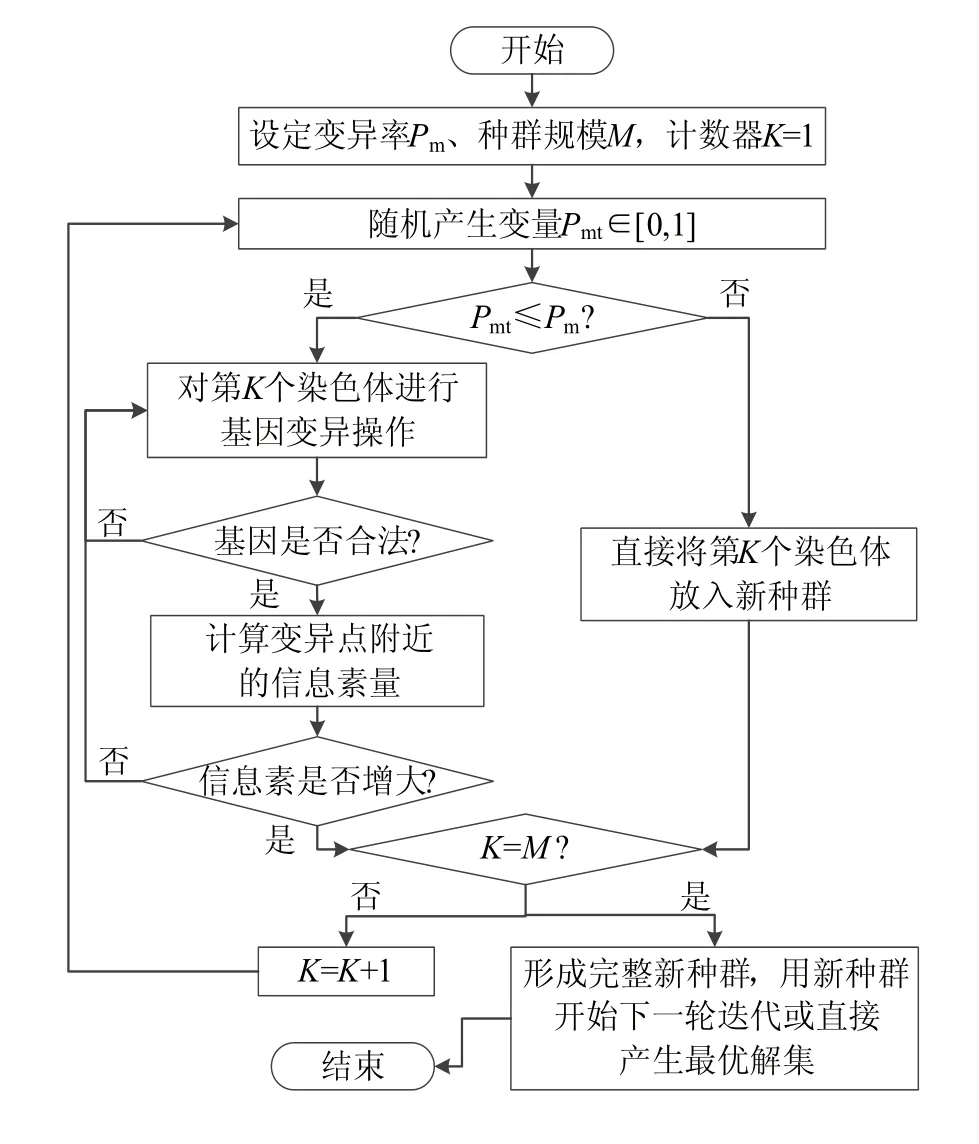
图3 变异操作流程

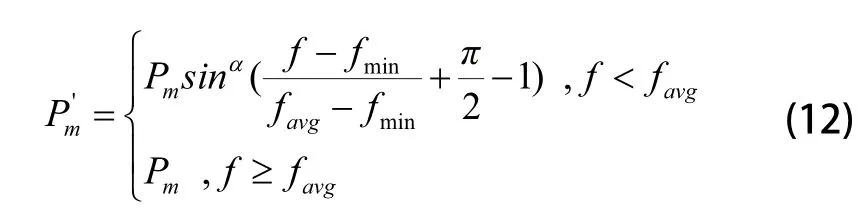
其中：P'm表示修正后的变异率；f表示被选个体的适应度值；favg表示种群中平均适应度值；fmin表示种群个体中的最小适应度值；α表示调整参数，取值范围由问题适应度值范围决定。

当个体的适应度值高于平均适应度值时，则按照正常变异率进行变异；当低于平均适应度值时，说明该个体在种群中较优质，则适当降低变异率。对变异率进行修正的意义在于保证了在同一代下相对较优的个体有更小的几率进行变异操作，从而在不失种群多样性的基础上保护了优良的个体，促进了运算后期算法的逐步收敛和稳定。

3.6 其他参数设定

1）种群规模

种群规模M指群体中个体的数量，一般认为种群规模会影响算法的运算效率和效果。种群规模的选取与问题的规模相对应，M选取较大易增加算法的运算负担，较小则抑制算法的活性。在以实数编码方式的遗传算法中，M的大小通常与染色体长度n存在一定的关联性，取值范围区间为[1.5n,2n/2]。

2）终止条件

终止条件通常由设定好的迭代次数N决定。随着迭代次数的增加，较优解在种群中所占的比例会逐渐增大，此时称种群逐渐趋于收敛。在实际运算中，迭代次数N需要多次试算进行确认。

4 实例验证

某型号齿轮的生产制造过程主要包括：粗车、精车、钻孔、铣齿、倒角、磨孔、研磨和配对等八项任务，每项任务都要用到不同的加工设备。设定加工100件该型号齿轮。现在任务发起人欲通过云平台在资源池中搜索所有符合该任务加工作业的设备资源，同时综合考虑交付时间、加工成本和加工质量等目标，获得较优的资源配置方案。通过对云资源池中的相关制造资源进行选取，得到了每类资源的若干相似度较高的个体，如表1所示。所有资源都分布在A、B、C和D四个区域，设定最终交付地为E，区域之间的运输时间和费用关系如表2所示。

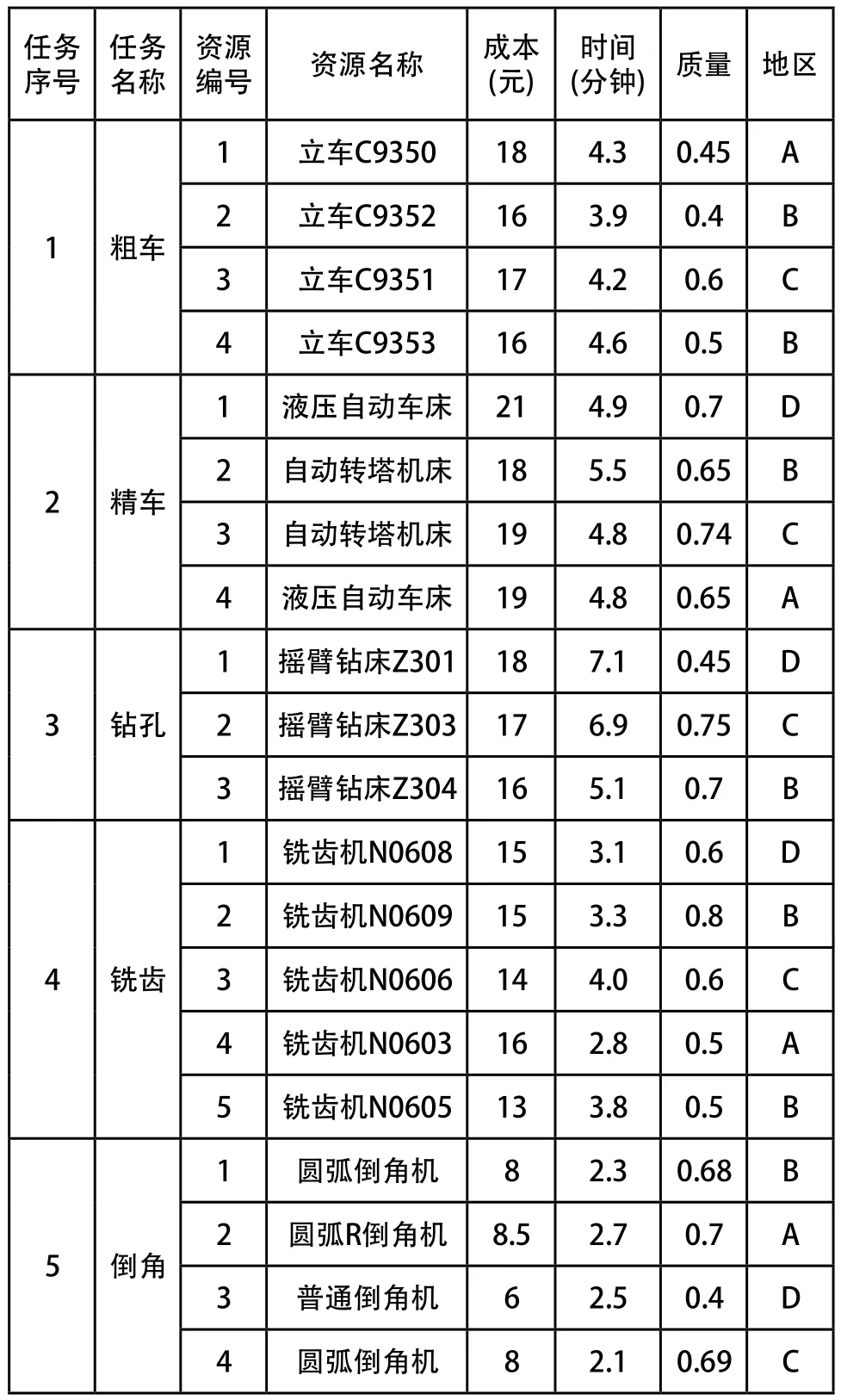
表1 加工资源数据

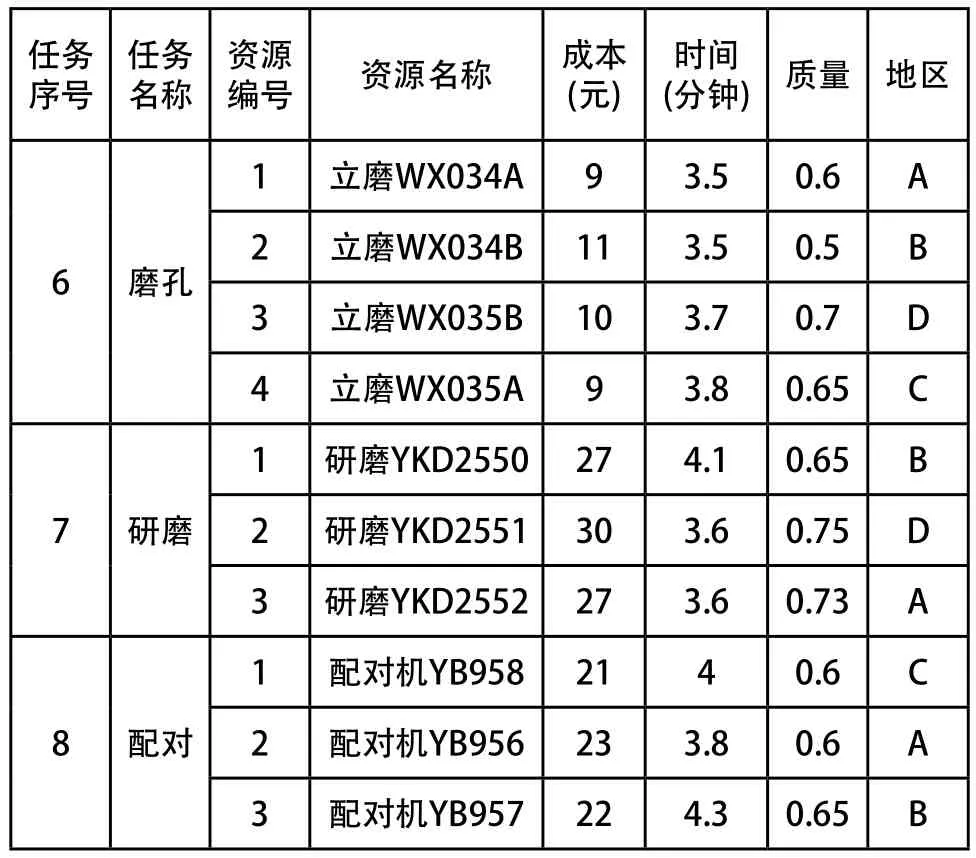
续（表1）

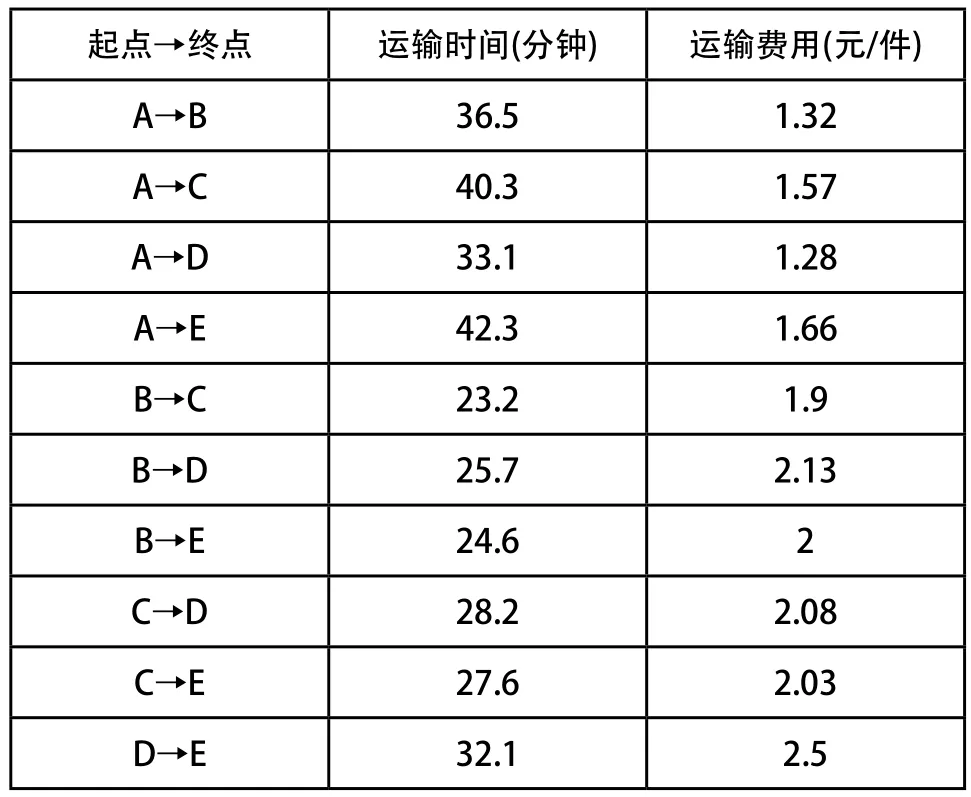
表2 区域关系

运用C#编程语言设计适应于该问题的传统遗传算法与改进型遗传算法，其中传统遗传算法采用轮盘赌法进行选择操作，改进型遗传算法采用混合轮盘赌+锦标赛选取法。对上述研究问题进行优化配置，主要步骤如下：

步骤1：依照式(6)建立评价函数模型。在本实例中，Tmax和Cmax为动态值，经过前期多次试算，得到试算值分别为3755和15747。在该值基础上进行一定的增值，可防止计算过程中适应度值的非法溢出（＞1）。本文设定Tmax取值为3760，Cmax取值为15750。Qmax在本实例中为静态值，直接求得结果为5.69。设定各个优化目标的权重值为：ωT=0.3，ωc=0.4，ωQ=0.3。

步骤2：对问题进行编码，得出染色体长度n为8，结合染色体长度与种群规模的关系，设置较为理想的M为14。通过随机方式生成合法初始种群，用矩阵表示为

步骤3：经过前期多次试算，设定两种算法的迭代次数为80次。考虑到M设置不大，为保证解的多样性，在选择操作中设置Ct为3，同时设定传统遗传算法的Pc为0.5、Pm为0.2，改进型遗传算法的Pc1为0.5，PcN为0.2。考虑到改进型遗传算法在变异过程中引入了正反馈机制，因此采用双点变异的方式，设定Pm为0.2、α为2以增强算法优化方向。

步骤4：通过迭代运算得到两种算法的适应度函数值收敛趋势以及最终优化结果，如图4所示。

图4 资源优化配置结果

在图4中，线条TGA代表传统遗传算法，AGA代表改进型遗传算法。由于改进型遗传算法在选择操作中采用了轮盘赌和锦标赛混合选取法，并在变异过程中加入了正反馈特性，明确了变异的优化方向，因此选择优良个体的能力明显强于传统遗传算法，从而收敛速度明显加快，且保证了种群多样性，使得计算过程逐渐趋于最优。同时改进型遗传算法的交叉率和变异率受迭代次数和适应度值的影响而自适应调整，在不失活性的同时保证了运算后期对优良个体的保护，因此比传统遗传算法更稳定，也更易获得最优解。最终通过改进型遗传算法得到资源的最优配置结果，用染色体编码表示为X={3,3,3,2,1,1,3,2}。

任务集中每项任务所选择的资源编号为染色体X中对应的基因序号，因此得到资源的最优配置依次为：

立车C9351→自动转塔车床（编号3）→摇臂钻床Z304→铣齿机N0609→圆弧倒角机（编号1）→立磨WX034A→研磨YKD2552→配对机YB957。

5 结束语

随着云制造的发展，制造资源和制造任务海量化、多元化的趋势日益明显，资源与任务之间的快速配置难度增大。针对传统遗传算法在求解制造资源配置问题时存在盲目迭代、求解效率低、收敛速度慢等问题，对遗传算法进行优化改进，提出了一种轮盘赌法和锦标赛法相结合的选取机制，并赋予变异过程正反馈特性，明确了优化方向，提高了寻优效率。同时采用交叉率和变异率自适应的方法，在确保算法不失活性的前提下优化了求解过程，提高了算法的收敛性和稳定性。最后以某型号齿轮的生产加工过程为例验证了本文所提模型和改进算法的有效性。基于改进型遗传算法，提出制造资源优化配置方法，为云模式下多主体业务协同和制造资源优化共享提供了新思路。

[1]李伯虎,张霖,王时龙,等.云制造—面向服务的网络化制造新模式[J].计算机集成制造系统,2010,16(1)：1-7.

[2]尹胜,尹超,刘飞,等.多任务外协加工资源优化配置模型及遗传算法求解[J].重庆大学学报,2010,33(3)：49-55.

[3]Kundakci Nilsen, Kulak Osman. Hybrid genetic algorithms for minimizing makespan in dynamic job shop scheduling problem [J].Computers & Industrial Engineering,2016,96：31-51.

[4]袁庆霓,谢庆生,许明恒,等.Web服务平台下基于遗传算法的制造资源服务选择[J].计算机应用研究,2009,26(4)：1266-1268.

[5]张雪艳,梁工谦,董仲慧.基于改进自适应遗传算法的柔性作业车间调度问题研究[J].机械制造,2016,54(6)：1-4.

[6]陶飞,张霖,郭华,等.云制造特征及云服务组合关键问题研究[J].计算机集成制造系统,2011,17(3)：477-486.

[7]MR Garey, DS Johnson. Computers and Intractability： A Guide to the Theory of NP-Completeness[M].New York：W.H.Freeman and Company,1979.

[8]付景枝,张友良.基于遗传算法的网格制造资源优化选择[J].小型微型计算机系统,2007,28(4)：674-677.

[9]杜轩,李登桥,朱康.基于矩阵编码遗传算法的PCB生产线元件分配优化[J].三峡大学学报,2015,37(1)：89-93.

[10]马雪芬,戴旭东,孙树栋.面向网络化制造的制造资源优化配置研究[J].计算机集成制造系统,2004,10(5)：523-527.

[11]翟梅梅.基于蚁群算法的改进遗传算法[J].安徽理工大学学报,2009,29(3)：58-63.