基于SolidWorks的吊钩有限元分析

李 鹏

（山西工程职业技术学院 基础部， 太原 030009）

吊钩是起重机必备的部件之一，发挥着连接重物与起重机的连接作用。由于其频繁遭受各种载荷，一旦发生损坏极易造成重大人员财产事故，因此对于吊钩的安全性应引起足够的重视。传统理论计算将吊钩简化为平面模型，应用弹性曲梁理论，对工作应力进行计算。此方法计算不能反映吊钩真实情况。应用现代有限元分析法，通过将模型划分为若干个单元即将模型离散化，利用简单问题代替复杂问题进行求解，对吊钩进行强度分析，观察吊钩应力分布情况，从而找出吊钩的危险截面[1]。

SolidWorks是一个简单、易学、易用的三维参数化设计软件，广泛应用于机械领域。SolidWorks不光图形绘制功能强大，其内置的Simulation插件更可以对绘制的三维模型进行有限元分析，相比于ANSYS进行有限元分析，SolidWorks建模更为方便迅速，并省去了模型导入过程。

1 理论计算

吊钩根据制造方法可分为锻造吊钩和片式吊钩。本文主要对锻造单钩，钩号为08的MMD型，额定起重量为2 t，强度等级为T级进行分析。此吊钩断面形状类似于T字形，由于这样结构可以充分利用材料性能，且自重相对于梯形截面吊钩更轻，即使生产工艺稍复杂仍被广泛应用[2]。

根据吊钩工作状态可知，在吊钩上A-A是危险截面（见图1），最大应力在截面的内侧，应力主要为拉伸应力和弯曲应力之和，而外侧为拉伸应力与弯曲应力之差，应力相对内侧较小。故理论计算出A-A截面内侧应力，判断是否超出材料屈服应力，并与Simulation求出最大应力做对比。吊钩截面图见图2。

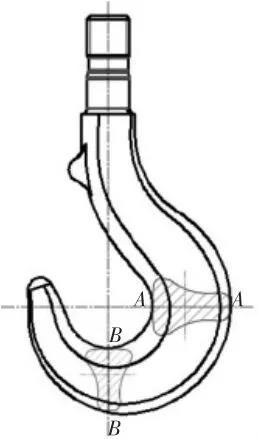
图1 吊钩模型

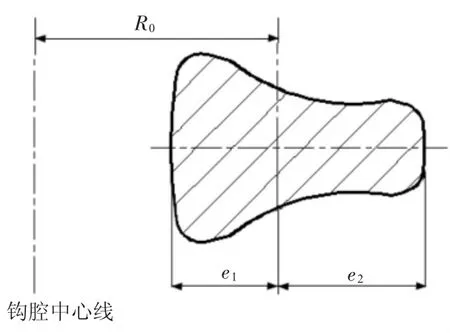
图2 吊钩截面

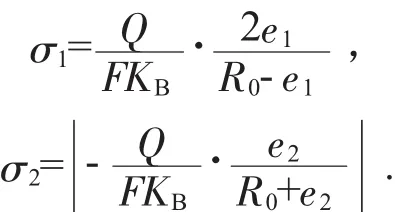
式中：σ1为 A-A 截面内侧的应力，MPa；σ2为 A-A截面外侧的应力，MPa；Q为吊钩牵引重物的重力，N；F为截面的面积，mm2；KB为截面的曲梁系数，F（x为计算 KB值自变量）；R0为截面重心轴线至吊钩中心线距离，mm；e1为截面重心至吊钩内缘距离，mm；e2为截面重心至吊钩外缘距离，mm[3]。

本文研究的吊钩额定起重量为2 t，换算为重力可得Q=19 600 N。由于吊钩截面有倒角，且两侧有切除部分，个别文献对于其面积按梯形面积公式计算显然存在较大误差。对于截面面积计算完全可以利用SolidWorks软件中测量插件对截面面积进行查看，结果准确且方便，本截面F=938.70 mm2。对于R0、e1、e2值的确定关键在于找到截面的重心，使用梯形重心公式求其重心存在误差，可利用SolidWorks将截面拉伸为实体，利用软件内置质量评估功能查看其重心，求得：R0=42.63 mm，e1=18.63，e2=25.76。通过计算KB=0.079。

即吊钩危险截面处外侧最大应力为410.33 MPa，内侧应力为99.56 MPa。

2 吊钩模型的建立

根据查询吊钩标准，按照国标推荐尺寸绘制吊钩三维模型。首先建立弯钩模型，在其中的几个位置绘制截面草图，采用放样命令，依次选中绘制的截面，并绘制出外形轮廓作为引导线，注意两条引导线应设立在两个草图中。吊钩钩颈部分采用拉伸和拉伸切除以及倒角命令生产，螺纹处采用装饰螺纹线表示，以简化模型[4]。吊钩模型的建立见图3.

3 有限元分析过程

3.1 定义材料属性

钩号为08的吊钩采用35CrMo材料可以使其达到较高的强度等级，在SolidWorks中定义材料属性：弹性模量为2.13×105MPa，泊松比为0.286，质量密度为7 870 kg/m3，屈服强度为835 MPa。

3.2 添加约束与载荷

吊钩通过钩颈的螺纹与上方的零件连接，分析过程将此部分固定，以方便求解吊钩复杂模型。吊钩吊起重物，受力应垂直向下，吊钩通过钢丝绳与重物连接，故作用点应在吊钩口中心下方位置。通过应用分割线命令将吊钩中心垂直下方正负45°范围内全面分割，在此面内施加19 600 N垂直向下应力。

3.3 划分网格

在软件中选择高品质网格，单元大小为2.982 mm，公差为0.149 104 mm，共有70 528节点，单元数为47 192。吊钩网格划分结果见图4[5]。

3.4 计算结果分析

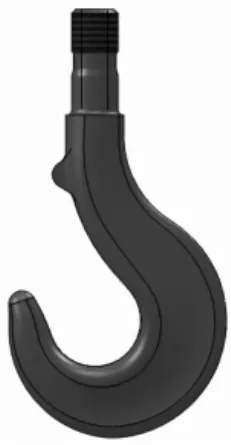
图3 建立吊钩模型

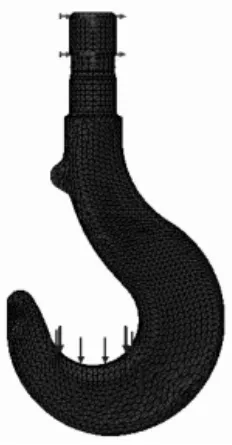
图4 吊钩网格划分结果

点击运行按钮，可得到SolidWorks模拟算例计算结果。应力分布情况如图5，吊钩工作状态下在竖直方向收到向下的重物拉力，由于吊钩形状的特性，吊钩弯曲部分还受到弯曲应力，从图5来看，印证了这一观点，吊钩的危险截面位于吊钩中心内侧，其所受应力为拉应力与弯曲应力之和，此处最大应力为418.898 MPa，应力沿远离中心的方向急剧减小，设计吊钩时应着重考虑此处的应力。通过理论计算与SolidWorks仿真分析，得到了一致的结果，即吊钩A-A截面内侧为吊钩危险截面。理论计算结果吊钩最大应力为410.33 MPa，仿真分析结果为418.898 MPa，两者的误差基本可以忽略，误差的可能原因为危险截面处的应力集中，且在仿真分析时，添加载荷的位置也可对结果造成影响。吊钩采用的材料35CrMo屈服强度为835 MPa，理论计算与仿真分析值均在屈服强度之内，因此该吊钩可以满足强度要求[6-8]。

根据图6位移云图可以观察到由于吊钩受到重物拉应力以及弯曲应力影响，吊钩前段位置发生最大位移，位移值为0.478 mm。此位移值会使吊钩发生一定程度的形变，但是由于其数值较小，因此不会对吊钩正常工作产生影响。

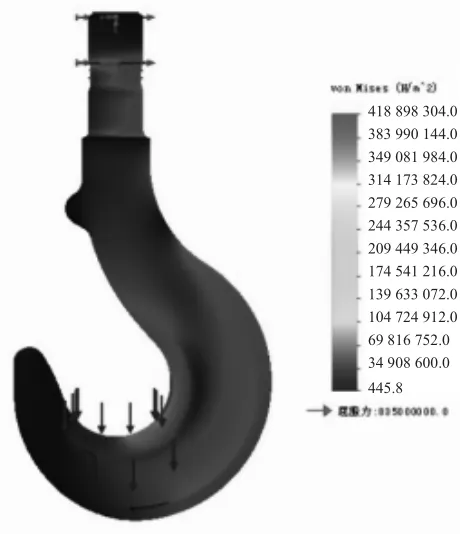
图5 有限元分析应力云图

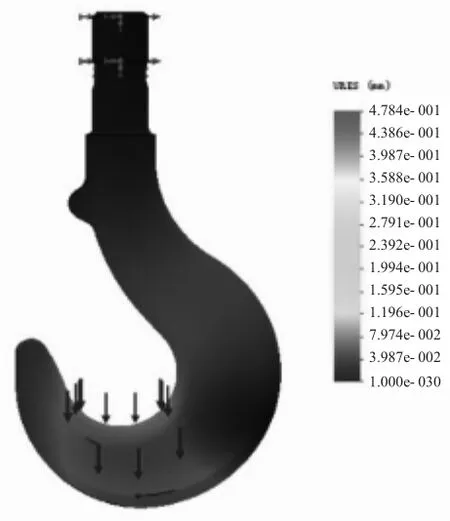
图6 有限元分析位移云图

4 结语

1）通过应用SolidWorks软件构建三维模型，运用自带Simulation有限元分析快捷方便，相比于三维建模之后导入Ansys不会出现模型构建错误。

2）应用Simulation插件对吊钩进行有限元分析可以得到与理论计算相一致的结果，易损部位在吊钩内侧弯曲处，吊钩的设计与使用过程应着重分析此处，并应不定期对吊钩进行安全检查，保证使用安全。

3）相比于理论计算，利用SolidWorks有限元分析可以得到各个点的精确解，并可以直观观察应力分布情况。通过SolidWorks软件对模型进行设计、分析可以降低生产成本、缩短生产周期。

[1] 白学勇，黎姝，李勇刚.基于ANSYS软件的吊钩有限元分析[J].煤矿机械，2009（11）：86-87.

[2] 李水水，李向东，范元勋，等.基于ANSYS的起重机吊钩优化设计[J].机械设计与制造，2012（4）：37-38.

[3] 刘鸿文.材料力学[M].北京：高等教育出版社，2004.

[4] 闫兴明，张亮有.基于SolidWorks起重机吊钩的有限元分析[J].机械工程与自动化，2016（1）：44-45.

[5] 李锋，权延慧.基于Pro/E的吊钩有限元分析[J].山西电子技术，2010（6）：14-15.

[6] 锅彦娣，李振纲.基于ANSYS的起重机吊钩强度分析[J].煤矿机械，2016，37（12）：45-46.

[7] 王谦，赵俊利.基于SolidWorks软件的吊钩分析[J].煤矿机械，2011，32（10）：130-131.

[8] 陈昱璇.基于静强度和疲劳强度的起重机吊钩分析与研究[D].太原：太原科技大学，2015.