换热器管板设计中当量实心板理论的发展概述

刘雪梅 杨国政 张学勇 杨星辰

（航天长征化学工程股份有限公司）

0 前言

换热器是用于不同温度流体之间热量传递的装置，是石油化工等行业广泛使用的重要设备。大型管壳式换热器中的换热管较多，工况较复杂。其中管板是换热器中受力最为复杂的部件，管板的设计是换热器设计中的重要环节。

早期由于条件的限制，无法直接对换热器管板进行分析，因此将管板视为受均布载荷作用、具有有效弹性模量和有效泊松比的圆形平板，以弯曲受载为基础计算板中最大应力。很多标准体系采用了这个理论并不断地进行改善，逐渐形成了现在的换热器管板常规设计方法。当量实心板理论在换热器管板的设计演变历程中扮演着相当重要的角色，本文即对当量实心板理论的发展历程进行相应的概述与总结。

1 当量实心板理论的研究概述

当量实心板理论是Gardner[1]于1948年在进行浮头式换热器设计时提出的概念，即将多孔板替换成具有相同尺寸以及等效抗弯刚度的实心板，然后根据圆平板理论求解管板应力。

1.1 三角形布管管板的有效弹性常数研究

早期人们主要对三角形布管管板的有效弹性常数进行研究，对于正方形布管管板的研究较少。1948年Gardner引入了管孔削弱系数μ和挠度系数η，管孔削弱系数μ表示管孔对管板的削弱程度，挠度系数η表示开孔对管板弯曲刚度D的削弱。设D*为多孔板削弱之后的当量弯曲刚度，则等效弯曲刚度 D*和管孔削弱系数 μ的表达式如式 （1）、式 （2）所示，其中所涉及的管孔模型如图1所示。

式中 p——管孔中心距；

d——管子外径。

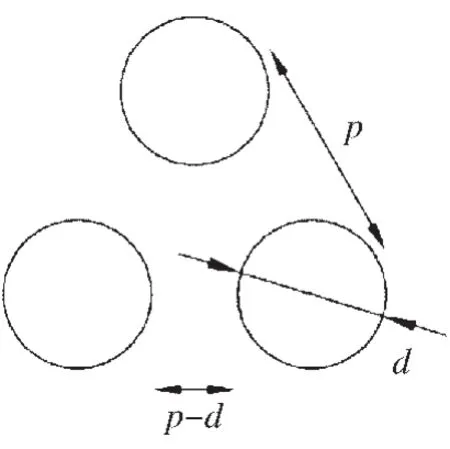
图1 管孔示意图

1952年，Gardner[2]将此方法应用到固定管板式换热器的设计中，但其不足之处在于未考虑管子对管板的支撑作用。

1952年，Miller[3]弥补了Gardner理论中的不足，考虑了管子对管板的支撑作用，将当量实心板视为置于弹性基础之上的圆平板并改进了挠度系数η的计算方法。同年，Malkin[4]与Horvay[5]采用等效方法导出了当量实心板的有效弹性模量E*与有效泊松比v*，并将E*/E和v*代替了当量实心板的抗弯刚度D*。

1959年和1960年，Sampson[6-7]使用光弹法对承受平面载荷和弯曲载荷的多孔板进行了实验，发现下述一些规律： （1）承受平面载荷时，有效弹性模量E*和多孔板弹性模量E之比E*/E和有效泊松比v*与多孔板的厚度h无关，且E*/E与多孔板所受载荷的方向无关，但v*呈现各向异性，其值随着载荷方向的变化而变化。 （2）承受弯曲载荷时，E*/E和v*呈现各向同性，两者在板厚与管孔中心距之比h/p＜2时，随着多孔板的厚度变化而发生显著的变化，但当h/p＞2时这种变化非常缓慢。当多孔板取较厚的厚度时，弯曲载荷作用下的计算结果接近平面应力状态下的计算值。

因此Sampson认为，板厚与管孔中心距的比值h/p=2是薄板和厚板的分界线。同年，Leven[8]通过实验验证了Sampson的结论。

1962年，O’Donnell等[9]在Sampson研究的基础上对h/p≥2的三角形布管的多孔厚板提出了有效弹性常数和管孔削弱系数μ的关系曲线，1966年ASMEⅢ和随后的ASMEⅧ-Div.2采用了这些曲线。

1969年，Meijers[10]对三角形布管、正方形布管的薄板 （h/p＜0.1）和厚板 （h/p＞2）承受平面载荷与弯曲载荷的情况做了研究，并得到了弯曲载荷作用下薄板和厚板的有效弹性常数。之后改进了弯曲载荷作用下薄板 （h/p→0）、厚板 （h/p→∞）与中间范围 （0＜h/p＜∞）有效弹性常数的确定方法[11]。这些成果已被很多压力容器设计标准 （英国BS 5500、法国CODAP、欧盟EN 13445和ISO等）所采用。

1.2 正方形布管管板的有效弹性常数及后续研究

20世纪60年代前，人们研究的是三角形布管管板的等效方法，60年代后开始研究正方形布管管板的等效方法。与三角形布管管板各向同性的有效弹性常数相比，正方形布管管板的有效弹性常数呈现各向异性，表现在对角线方向d和中心距方向p具有不同的有效弹性常数，如图2所示。

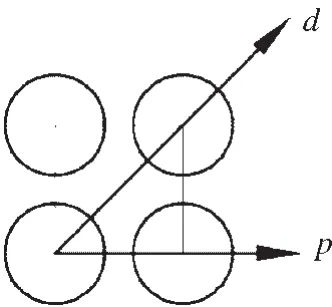
图2 正方形布管示意图

1960年，Bailey和Hicks[12]通过对不同管孔削弱系数μ的正方形布管的多孔板进行拉伸剪切实验，得到了当量实心板的有效弹性常数设计曲线，发现正方形布管的当量实心板有效弹性常数呈现各向异性。1967年O’Donnell[13]对正方形布管的多孔板进行了研究，使用理论方法证实了正方形布管的当量实心板弹性常数的各向异性，表现在中心距方向与对角线方向的有效弹性常数不同。

1971年，Slot和O’Donnell[14]研究了承受平面应力、平面应变和一般平面应变条件的三角形布管与正方形布管的多孔薄板和承受一般载荷的多孔厚板，发现对于正方形布管来说，管孔削弱系数μ在0.2≤μ≤0.4时比μ趋近于1时 （无限接近于不开孔板）的各向异性更为显著。文章给出了三角形布管当量实心板在不同泊松比时的有效弹性常数E*/E、v*与μ之间的关系图，以及不同泊松比时正方形布管对角线方向和中心距方向的有效弹性常数Ed*/Ed、vd*、Ep*/Ep、vp*与μ之间的关系图。最后将结果与Sampson光弹法实验结果、Meijers理论计算结果对比发现三者吻合很好，如图3所示。之后许多研究者做了相关的实验，实验结果表明Sampson的研究成果是准确的，而 Malkin与Horvay由于采取了几何近似，其计算值是不很准确的。

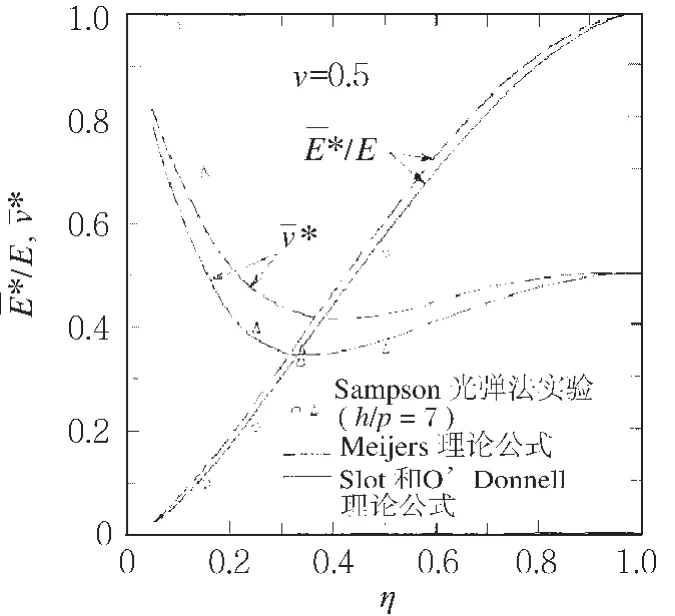
图3 Slot和O’Donnell的研究结果（与Meijers、Sampson的结果对比）

1972年，Slot[15]分别对承受平面载荷、反平面剪切载荷和热载荷的多孔厚板进行大量的分析与相应的实验，给出了大量的对比图表。1974年Slot和Branca[16]从非弹性角度入手，使用有限元方法模拟承受平面载荷和反平面剪切载荷下的三角形布管多孔板，研究了高温高压所导致的多孔板非弹性状态下的应力应变之间的关系。

1973年，O’Donnell[17]对一系列按照三角形和正方形排列开孔的铝制梁进行实验，模拟多孔板平面应力、平面应变和一般平面应变下的受载状态，通过实验与理论对比，得知可将厚板受载看作一般平面应变状态，非常薄的管板承受平面载荷时可看作平面应力状态。

对于不同的管孔削弱系数μ，尤其是当管孔削弱系数μ极大或者极小时，对当量实心板的有效弹性常数的影响是比较大的。1974年Porowski和O’Donnell[18]对三角形布管下不同管孔削弱系数的管板进行了研究，对削弱系数在0.05＜μ＜1范围内同时承受不同载荷的管板进行分析，研究了不同管孔削弱系数对管板的削弱程度；1975年两人[19]对正方形布管的管板做了同样的研究。

1977年，Porowski和O’Donnell[20]对管孔带处的塑性应变做了研究，通过有限元方法计算了不同管孔削弱系数下承受剪切载荷等载荷时的多孔板应力。

1978年，Porowski和O’Donnell[21]利用有限元方法对承受压力载荷和复杂热载荷的多孔板进行了研究，提出了三角形布管与正方形布管管板的轴对称分析时所用的弹性矩阵，如式 （3）所示：

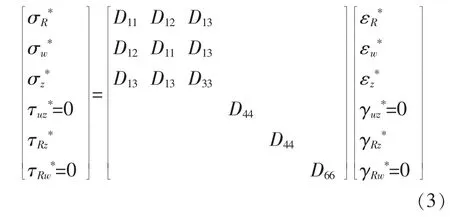
同时，还对各载荷情况下管孔的周边应力分布做了研究，给出了各种载荷情况下确定管孔周边峰值应力的局部应力因子曲线。

Sampson通过光弹法实验并分析结果后认为，板厚与管孔中心距比值h/p=2是薄板和厚板的分界线。因此确定多孔板当量实心板有效弹性常数可根据h/p的值来进行区分。综合了不同研究的实验和计算结果，可将板厚范围及相应的有效弹性常数确定方法划分如下。

（1）薄管板 （h/p＜0.1）：根据Meijers的研究成果[10-11]，结合实验值确定有效弹性常数。

（2）厚管板 （h/p＞2）：根据Slot和O’Donnell的研究成果[14]，结合实验值确定有效弹性常数。

（3）中间值管板 （0.1＜h/p＜2）：根据Meijers的研究成果[10-11]， 结合Sampson[7]与 O’Donnell[17]的实验结果确定有效弹性常数。

1989年，Osweiller[22]对过去几十年来当量实心板有效弹性常数的研究和发展做了全面的回顾，并把当量实心板有效弹性常数的研究分为三阶段。

（1）第一阶段为1948年—1959年，主要使用等效简化方法来确定有效弹性常数，为经验阶段。此时由于理论不完善导致不同研究者的计算结果有较大的差异。

（2） 第 二阶段 为 1960年—1962年 ， 以Sampson光弹法实验研究成果为代表，通过实验得到了三角形布管管板在承受平面载荷和弯曲载荷时有效弹性常数和管孔削弱系数之间的关系曲线。

（3）第三阶段为1963年—1985年，此阶段提出了更为精确的理论以及增加了计算机的使用，同时加入了之前并未考虑的正方形布管管板的有效弹性常数问题，通过大量的实验和理论计算，得到了准确的有效弹性常数计算曲线。

同时Osweiller提出，在满足特定条件下依然可以将正方形布管的多孔板看作各向同性处理，此时正方形布管当量实心板的各向同性有效弹性常数可以通过各向异性的有效弹性常数来表示，其计算式如式 （4）和式 （5）所示：

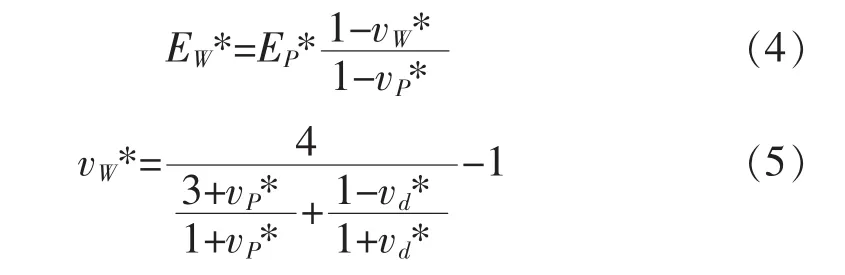
1996年，Ukadgaonker等[23]从力学、实验和数值分析三个方面对换热器管板的有效弹性常数研究历程做了综述，提出了未来的一些发展方向。

1.3 国内有效弹性常数的研究成果

国内的研究者对当量实心板的有效弹性常数也有所研究。1981年，清华大学钱伟长和戴福隆[24]在Horvay研究基础上对计算模型进行了合理简化，并考虑了等效板梁之间的约束作用，导出了厚管板的有效弹性常数，如式 （6）和式 （7）所示：

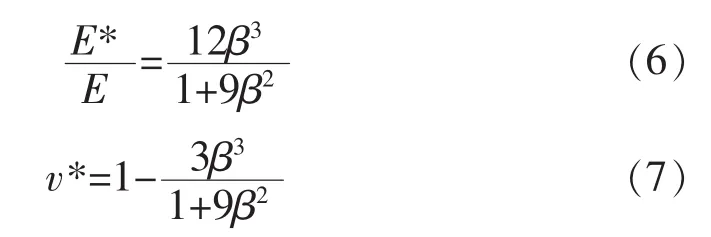
式中 β——六边形网格板的管孔削弱系数，且β=b/p；

b——六边形网格板板梁的平均宽度；

p——管孔中心距。

将计算所得的有效弹性常数与Sampson和Slot的结果对比，发现在很大范围内吻合较好，通过实验也验证了其可靠性。

1992年，黄克智和薛明德等[25]在国外研究人员研究基础上考虑了管子对管板的加强作用，在考虑管子胀接或者焊接对管板加强作用的前提下计算了管板应力，发现此结果更加符合实验结果。

2004年，谢桂兰等[26]使用复合材料中广泛应用的多尺度均匀化理论计算了管板有效弹性常数，发现对于平面问题来说使用均匀化理论计算所得有效弹性常数与ASME相应曲线吻合较好。

2010年，王珂等[27]通过固有频率等效、挠度等效和应变能等效三种方法计算了多孔板的有效弹性常数，同时将三种方法与ASME的计算结果进行对比，对比结果显示三种方法与ASME的结果均能对应一致，且都能处理复杂多孔管板如非圆孔管板结构的有效弹性常数。

总之，当量实心板有效弹性常数的理论及其主流研究方向由西方研究所引领，国内关于此方面的研究很少且相对滞后。

2 当量实心板理论在标准中的应用

当量实心板理论被很多标准所应用，如美国的TEMA与ASME、英国BS 5500、法国CODAP和欧盟EN 13445等。ASME标准由于其权威性且在国内应用十分广泛，因此本文仅对ASME体系进行详细的介绍。

ASME标准中换热器设计部分的历史并不久，1980年ASME第一次正式推出仅限于U形管换热器的管板设计章节，并将其作为非规定性附录AA列入ASMEⅧ-1。在1982年冬季增补和1992年Appendix AA-2中，加入了固定管板式换热器的管板设计方法。2003年ASME将Appendix AA列为强制性章节ASMEⅧ-1 UHX。经过几十年的发展，ASME标准中关于换热器的设计已经分别发展为ASMEⅧ-1 UHX章节与ASMEⅧ-2的4.18章节，这两部分的内容基本相同，均基于相同的理论基础。

ASME中换热器的设计是基于当量实心板理论的，其管板有效弹性常数的确定主要参考以上学者的研究，同时做了一些改进。ASME根据管板布管的实际情况，考虑了胀管与否、管板不布管带和温度等因素对管板的影响，采用了有效管孔削弱系数μ*来计算有效弹性常数。其中μ*的表达式为：

式中 p*——有效管孔中心距；

d*——管孔有效直径。p*和d*的表达式分别如式 （9）和式 （10）所示：

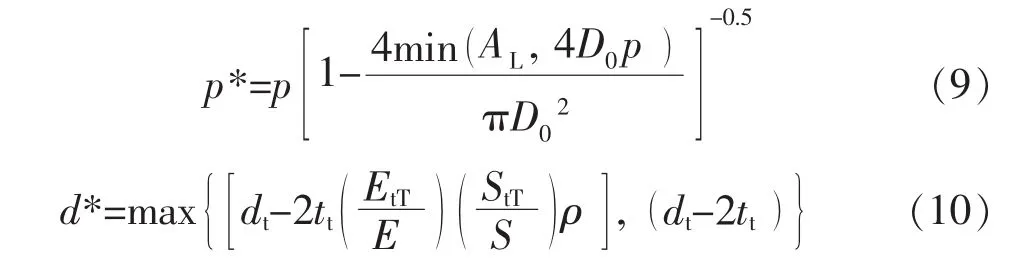
式中 AL——不布管带总面积；

D0——管板外排管子布管范围圆当量直径；

Dt——管子公称外径；

E——管板设计温度下管板材料的弹性模量；

EtT——管板设计温度下换热管材料的弹性模量；

p——管孔中心距；

S——管板设计温度下管板材料的许用应力；

StT——管板设计温度下换热管材料的许用应力；

tt——管子公称厚度；

ρ——胀管深度比。

前文提到1989年Osweiller提出在满足特定条件下依然可以将正方形布管的多孔板看作各向同性处理，因此在ASMEⅧ-1 UHX章节与ASMEⅧ-2的 4.18章节中，三角形布管与正方形布管管板的有效弹性常数的求解依然按照各向同性计算，但在ASMEⅧ-2 Annex-5.E章节中，依然保留了正方形布管管板各向异性有效弹性常数的计算方法。

总之，当量实心板理论从20世纪40年代末半经验等效简化开始，经理论的完善以及大量的实验对有效弹性常数计算方法进行不断的修改与完善，ASME根据前人的研究成果加以更全面的完善与补充，形成了今日ASMEⅧ-1&2章节中所使用的有效弹性常数求解方法。

3 当量实心板理论在分析设计中的应用

有限元法自提出后，经几十年发展已经相当成熟，工程界也越来越多地使用有限元法对换热器进行分析设计。对于大型的换热器来说，建模难易程度与计算规模大小是影响换热器分析设计效率的主要因素，因此为了提高工作效率，通常会对换热器进行一定的简化，然后再进行分析计算。

通常来说，换热器的简化分析就是根据当量实心板理论先将管板简化，再对其他部件进一步简化，然后再进行分析设计。换热器的简化算法前人研究很多。刘俊明[28]在不考虑管子支撑情况下将模型简化成轴对称模型进行计算。陈罕[29]将管子和管板替换成8个同心圆筒和实心板建立轴对称模型，对环形管板的应力进行了研究。Weiya Jin等[30]建立了当量实心板和杆单元、管单元分别组合的模型进行计算，并进行了对比。杨国政[31]采用Beam 188和Solid 45单元分别模拟换热管和当量实心板，通过MPC技术连接两者进行了模拟计算。钱才富[32]使用壳单元和梁单元分别对当量实心板和换热管组合建模，模拟了管板的四分之一模型。庞心宇[33]将管板等效为实心板，换热管等效成同心圆筒，建立了轴对称模型，对换热器管板的应力进行了分析。

上述的简化算法均是建立在当量实心板理论基础之上的，不难看出当量实心板理论在换热器分析设计中也扮演着重要的角色。

4 总结与展望

通过对当量实心板理论的发展历程的回顾可知，当量实心板理论从提出至广泛应用于换热器设计并被标准采用，经历了经验简化阶段、理论实验验证阶段和精确计算阶段，是一个循序渐进、不断改进的过程。经过数十年的发展，当量实心板理论已经相当成熟，且组合进了换热器设计标准的基础理论部分。当量实心板理论在换热器的分析设计中也应用颇为广泛，通过对计算模型进行一定程度的简化，可提高分析设计的效率。因此，可以预见在今后的换热器设计中当量实心板理论仍将扮演相当重要的角色。

[1] GARDNER K A.Heat-exchanger tubesheet design[J]. Journal of Applied Mechanics，1948，70：377-385.

[2] GARDNER K A.Heat-exchanger tubesheet design 2[J]. Journal of Applied Mechanics，1952，74：159-166.

[3] MILLER K A G.The design of tube plates in heat exchanger[J].Proceedings of the Institution of Mechanical Engineers，Part B：Journal of Engineering Manufacture，1953（18）：215-231.

[4] MALKIN I.Notes on a theoretical basis for the design of tubesheet of triangular layout[J].ASME Journal of Applied Mechanics，1952，74：387-396.

[5] HORVAY G.The plane-stress problem of perforated plates [J].ASME Journal of Applied Mechanics，1952，19（3）：355-360.

[6] SAMPSON B C.Photoelastic frozen stress study of the effective elastic constants of perforated materials[M]. Westinghouse Electric Corp Research Labs，Pittsburgh，United States：1959.

[7] SAMPSON B C.Photoelastic analysisin perforated material subjected to tension or bending [J].Bettis Technical Review，1960.

[8] LEVEN M M.Photoelastic determination of stress in tube sheets and comparison with calculated values [J].Bettis Technical Review，1960：53-73.

[9] O’DONNELL W J，LANGER B F.Design of perforated plates[J].Journal of Engineering for Industry，1962，84（3）：307-319.

[10]MEIJERS P.Plates with a doubly periodic pattern of circular holes loaded in plane stress or in bending[C]// 1st International Conference on Pressure Vessel Technology，Part I，paper 1-44，1969：551-570.

[11]MEIJERS P.Refined theory for bending and torsion of perforated plates [J]. Journal of Pressure Vessel Technology，1986，108（4）：423-429.

[12]BAILEY R，HICKS R.Behavior of perforated plates under plane stress[J].Journal of Mechanical Engineering Science，1960，2（2）：143-165.

[13]O’DONNELL W J.A study of perforated plates with square penetration pattern[R].Welding Research Council Bulletin 124，1967：1089-1101.

[14]SLOT T，O’DONNELL W J.Effective elastic constants for thick perforated plates with square and triangular penetration patterns [J].JournalofEngineering for Industry，1971，93（4）：935-942.

[15]SLOT T.Stress analysis of thick perforated plates[M]. Westport，Conn：Technomic Publishing Co Inc，1972.

[16]SLOT T，BRANCA T R.On the determination of effective elastic-plastic properties for the equivalent solid plate analysis of tube sheets[J].Journal of Pressure Vessel Technology，1974，96（3）：220-227.

[17]O’DONNELL W J.Effective elastic constants for the bending of thin perforated plates with triangular and square penetration patterns[J].Journal of Engineering for Industry，1973，95（1）：121-128.

[18]POROWSKI J S，O’DONNELL W J.Effective plastic constants for perforated materials [J].Journal of Pressure Vessel Technology，1974，96（3）：234-241.

[19]POROWSKI J S，O’DONNELL W J.Plastic strength of perforated plates with square penetration patterns[J]. Journal of Pressure Vessel Technology，1975，97（3）：146-154.

[20]POROWSKI J S，O’DONNELL W J.Plastic strain concentration in ligaments[J].Journal of Pressure Vessel Technology，1977，99（2）：328-336.

[21]POROWSKI J S，O’DONNELL W J.Elastic design methods for perforated plates [J].Journal of Engineering for Power，1978，100（2）：356-362.

[22]OSWEILLER F.Evolution and synthesis of the effective elastic constants concept for the design of tubesheets[J]. Journal of Pressure Vessel Technology，1989，111（3）：209-217.

[23]UKADGAONKER V G，KALE P A，AGNIHOTRI Mrs N A， etal.Review ofanalysisoftube sheets[J]. International Journal of Pressure Vessels and Piping，1996，67（3）：279-297.

[24]钱伟长，戴福隆.厚管板的等效弹性常数[J].力学学报，1981，17（4）：364-371.

[25]HWANG K C，XUE M D，WEN X F，et al.Stresses of thick perforated plates with reinforcement of tubes and their effective elastic constants[J].Journal of Pressure Vessel Technology，1992，114（3）：271-279.

[26]谢桂兰，张平，龚曙光，等.基于均匀化理论的管板有效弹性常数的研究 [J].应用力学学报，2004，21（3）：129-133.

[27]王珂，刘彤，董其伍.复杂多孔板有效弹性常数的结构分析方法[J].压力容器，2010，27（5）：10-14.

[28]刘俊明，陈旭.高压厚管板的有限元分析计算 [J].压力容器，1997，14（2）：25-29，90.

[29]陈罕，周昆颖，程瑞琳.蒸发器环形管板应力的有限元分析 [J].北京化工大学学报 （自然科学版），1995，22（1）：44-48.

[30]JIN W Y，GAO Z L，LIANG L H，et al.Comparison of two FEA models for calculating stresses in shell-and-tube heat exchanger [J].International Journal of Pressure Vessels and Piping，2004，81（6）：563-567.

[31]杨国政.基于ANSYS斜锥壳固定管板釜式重沸器有限元分析[D].天津：河北工业大学，2007.

[32]QIAN C F，YU H J，YAO L.Finite element analysis and experimentalinvestigation oftubesheetstructure[J]. Journal of Pressure Vessel Technology，2008，131（1）：011206-011209.

[33]庞心宇.换热器管板结构分析方法及轻量化研究 [D].湘潭：湘潭大学，2013.