基于圆弧边缘特征的圆检测算法

，

(浙江工业大学 信息工程学院，浙江 杭州 310023)

在机器视觉领域中，圆检测是一种重要的检测手段.圆检测的方法有很多种，应用最广泛的圆检测是Hough变换.Hough变换不仅可以用在检测直线[1]、PCB板的圆Mark点定位[2]以及焊孔缺陷的检测[3]上，还可以用在图像的倾斜矫正[4]上.Hough变换的抗干扰能力强，是圆检测的常用算法.由于当Hough变换的参数空间大于或等于三维时(比如检测圆)，Hough变换的计算量和所需内存大小将大大提高.针对这些问题，Xu等[5-6]提出了随机霍夫变换，然而随机霍夫变换的随机采样会带来大量的无效采样和累积.舒龙庆等[7]提出了基于圆的对称性的圆检测算法.周冬跃等[8]提出了基于粒子群优化算法的快速圆检测算法.作为目前为止OpenCV中的唯一一种圆检测算法[9]，21HT将检测圆的过程分成了两部分，首先利用图像的梯度信息投票检测圆心，然后通过圆心计算半径，减少了霍夫空间的维度.因此，不仅21HT的内存占用比标准霍夫变换小，而且检测速度大大超越了标准霍夫变换.但是21HT的半径检测来源于圆心的检测，而圆心的检测依赖于稳定的局部梯度，如果梯度出现一些噪声，则不能正确地检出圆，并且21HT不能检测同心圆.为了解决这些问题，提出了一种新型的基于圆弧特征的圆检测方法.

目前，主流的圆检测算法对每个像素点都进行相同的检测，会产生大量无效的运算处理.文中新型的圆检测算法主要通过边缘信息分析来提取圆弧，先通过打断分叉边缘得到便于存储和分析的单向边缘链.从圆弧的特征出发，利用圆弧固有的特征，只提取具有圆弧特征的边缘进行圆检测，并通过对每一条圆弧坐标数据的有序存放从而实现高效并准确地处理圆弧坐标数据.通过最小二乘法和三点定圆相结合的方式提取圆弧边缘并得到每一条圆弧边缘对应的圆心坐标和圆半径.最后利用圆弧的圆心坐标和圆半径将属于同一个圆的圆弧进行聚类，并利用最小二乘法将其圆弧拟合得到所求圆.

1 基于圆弧边缘特征的圆检测算法

1.1 图像预处理以及边缘特征提取

在圆检测的过程中，图像预处理是一个非常重要的步骤.在实际中，待处理的图像是彩色的，首先，需要将彩色图像转化成灰度图，然后将灰度图进行高斯滤波，最后通过canny算子提取二值化边缘图像.

1.2 打断分叉边缘链

为了实现对圆弧特征边缘坐标的提取和有序存放，需要提取单方向的边缘链.在二值化边缘图像中，存在很多的分叉边缘，如图1所示，这些分叉链中有一些是圆弧边缘和其他边缘的重叠形成的，这些分叉的边缘不利于边缘链的存储和后期圆检测的进行.新的圆检测算法提出一种8邻域编码方法判断分叉点，并将分叉的连接点去除，从而获得无分叉的单一方向的边缘链.通过遍历可知，当边缘点的八邻域中值非零(即值为255)邻域数≤2时，该边缘点是必定不是分叉点，当非零邻域数≥5时必定是分叉点.当边缘点的非零邻域数为3或者4时采用查表法判断是否为分叉点.

图1 分叉边缘链Fig.1 Bifurcated edges

首先将8邻域进行编码，如图2所示.从左上角开始，从左到右，从上到下分别为1，2，4，8，16，32，64，128.计算值非零邻域数为3或者4的所有组合中邻域中心不是分叉点的非零邻域编码和，记录得到非分叉点编码表，如表1，2所示.

图2 8邻域编码表Fig.2 Coding table of eight neighborhoods

Table1Anonbifurcationpointcodingtablewith3neighbornumber

序号123456Ⅰ141925283842Ⅱ445256677073Ⅲ8498100112131137Ⅳ145146152193194200

表2八邻域中灰度值非零邻域数为4的非分叉点编码表

Table2Anonbifurcationpointcodingtablewith4neighbornumber

序号1234Ⅰ4660102116Ⅱ147153195201

然后对二值化图像图3(a)进行3×3窗口扫描图3(b)，得到8邻域中非零邻域数N，并将8邻域中值不是0的邻域编码累加得累加数S见图3(c)，如果非零邻域数N≤2，则认为该点不是分叉点，不对其做处理，如果非零邻域数为N=3或4，则查看累加数S是否在编码表中，如果S在编码表中则该点不是分叉点，如果不在编码表中则该点是分叉点并将该点像素点的值置为0.如果非零邻域数N≥5，则该点是分叉点并将该点像素点的值置为0见图3(d).经过以上的处理后，就可以将分叉连接点去除，将一条分叉链打断成多条单方向边缘链.

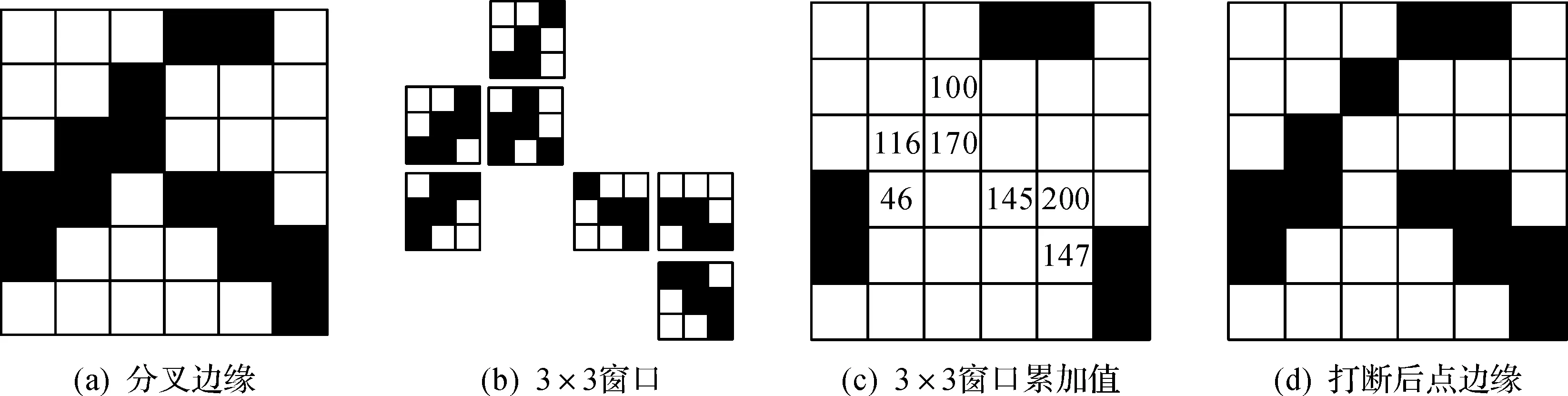
图3 去除连接点Fig.3 Removal of join points

1.3 类圆弧边缘链提取和有序存放

在1.2节得到的二值化边缘图像中，存在很多边缘链，有的边缘链是圆弧形成的(以下称这些边缘链为类圆弧)，有的边缘链是噪声引起，还有一些边缘链是圆弧和其他噪声边缘连接形成的，排除掉那些不是圆弧的边缘链对算法的速度和精度的提高有重大意义.因此，提出一种方法提取有效的类圆弧边缘链并且将边缘链按照边缘链生长方向存储在序列中.传统的圆检测算法中，并不是对边缘链进行处理的，而是对所有边缘坐标同一进行处理，导致增加了大量无效的运算.通过对边缘链的有序采集和存储从而对边缘链的有针对性的处理提供了基础.

研究圆弧的边缘链可以发现：将圆弧以水平直径开始每隔90度分成4部分，当按照从上往下的方向开始扫描时，左上部分圆弧的像素点走向只有向左、向左下和向下3种方向；右上部分圆弧的像素点走向只有向右、向右下和向下3种方向；左下部分圆弧的像素点走向只有向右、向右下和向下3种方向；右下部分的圆弧的像素点的走向只有向左、向左下、向下3种方向，如图4所示.

图4 圆弧像素的生长方向Fig.4 The growth direction of the pixels of the arc

从上往下扫描的时候，这4部分圆弧总共只有2种走向(向左、向左下和向下；向右、向右下和向下)，符合这2种走向的边缘链称为类圆弧边缘链.将符合这2种走向的边缘链提取出来可以避免处理大量无效边缘链，从而加快检测速度.新的圆检测算法优先提取向左、向左下和向下方向的边缘链，如果没有找到则再尝试提取向右、向右下和向下方向的边缘链.如果是一个完整的圆，经过检测算法后会被分成4条圆弧链分别保存在4个不同序列中.该方法将边缘链按照边缘生长方向存储在序列中，这将更加有效且快速地处理边缘链.以往的算法只能随机地选择点或者遍历所有的点来拟合圆就是因为没有将边缘链按照边缘生长顺序存储，不仅会引入大量的无效计算，而且精度也不高.新的圆检测算法将边缘链有序存储，方便后面处理边缘链的时候可以有选择地处理一些关键点坐标.这样可以提高处理的准确度和处理效率，减少处理时间.

通过这一步，将得到一个序列的集合，集合中的每一个序列都存着一个类圆弧的有序坐标序列.这里的有序是指每一个序列中的坐标都是按照类圆弧生长的方向存放的(比如序列的头和尾分别存放类圆弧的头坐标和尾坐标).

1.4 类圆弧初步检测

类圆弧检测之后，将这些序列按照序列的长度从大到小排序，将长度过小的序列从集合中除去.在1.3节得到的类圆弧链中，有一些不是真正的圆弧，在这部分中将去除不是圆弧的类圆弧.

如果类圆弧序列的长度为L，取出该序列的第一个坐标P1(x1,y1)，第L/4个坐标P2(x2,y2)，第L/2个坐标P3(x3,y3)，第3L/4个坐标P4(x4,y4)，序列的最后一个坐标P5(x5,y5).先通过P1，P3，P5三点求得圆心Cmax(cmx,cmy)及半径Rmax，通过P1，P2，P3求得圆心C1(cx1,cy1)和半径R1，通过P2，P3，P4求得圆心C2(cx2,cy2)和半径R2，通过P3，P4，P5求得圆心C3(cx3,cy3)和半径R3，求3个圆心距离的平方和得

Pdec=(cx1-cx2)(cx1-cx2)+(cy1-cy2)(cy1-cy2)+

(cx1-cx3)(cx1-cx3)+(cy1-cy3)(cy1-cy3)+

(cx2-cx3)(cx2-cx3)+(cy2-cy3)(cy2-cy3)

(1)

半径距离的平方和得

Rdec=(R1-R2)(R1-R2)+(R1-R3)(R1-R3)+

(R2-R3)(R2-R3)

(2)

Pdec与Rdec的比值为

Xdec=Pdec/Rdec

(3)

如果Pdec和Rdec同时小于一个设定的阈值TH1(与圆半径有关)，或者Xdec小于阈值TH2，则保留该类圆弧序列并执行第一步，否则将该类圆弧序列从集合中除去.

1.5 类圆弧精确检测

最小二乘法是一种常用的拟合方法，在工业中有着广泛的应用[10].最小二乘法也可以用于圆检测上[11].新的圆检测算法利用最小二乘法拟合与三点定圆相结合的方式筛选圆弧链.对每一条类圆弧序列分别使用最小二乘法拟合圆和三点共圆求得，拟合半径Rls，拟合圆心Cls(clsx,clsy)与三点共圆圆心Cmax(cmx,cmy)及半径Rmax.计算两种方法的偏差作为阈值对类圆弧进行筛选，即

Dp=(clsx-cmx)(clsx-cmx)+(clsy-cmy)(clsy-cmy)

(4)

Dr=(Rls-Rmax)(Rls-Rmax)

(5)

式中：Dp为的圆心坐标偏差度量；Dr为圆半径的偏差度量.如果Dp大于设定的阈值THdp或者Dr大于设定的阈值THdr，则将该序列从集合中删除.

1.6 合并同圆序列

聚类在圆拟合中是比较常见的[12].在圆检测中，残缺圆会形成一个或多个圆弧边缘，在检测过程中需要将同属一个圆的圆弧进行聚类以便后续处理.类圆弧序列中，为了找出同一个圆的所有圆弧边缘，可以利用半径和圆心坐标的偏差将类圆弧进行聚类，即

Dlsp=(clsx-cls2x)(clsx-cls2x)+(clsy-cls2y)(clsy-cls2y)

(6)

Dlsr=(Rls-Rls2)(Rls-Rls2)

(7)

式中：Dlsp为圆心左边偏差度量；Dlsr为圆半径偏差度量.集合中任意两条类圆弧序列如果满足Dlsp小于设定的阈值THdlsp且Dlsr小于设定的阈值THlsr，则认为这两条序列同属一个圆，将这两条类圆弧序列合并，直到集合中每一条序列中的坐标分别属于不同的圆.

1.7 排除短圆弧

将1.6节中得到的集合中的每一条序列分别作最小二乘法拟合圆，得到每一条序列中对应的拟合半径Rls以及拟合圆心(clsx,clsy).假设序列的坐标数为N，设阈值为THls，如果N<2πRls·THls，就将该序列从集合中删除.最后在每个序列中按一定间隔取坐标点计算其到拟合圆心距离以验证所得拟合圆的误差，将误差过大的序列从集合中删除.

通过以上步骤后，得到的集合中每一个序列对应的半径和圆心都是所求的圆.

2 算法流程

新的圆检测算法具体流程如下：

1)对进行图像预处理，得到二值化的边缘图像.

2)首先对边缘进行处理，将有分叉的边缘链打断成无分叉的单向的边缘链.

3)对边缘链进行类圆弧检测，并将检测到的类圆弧边缘链按照边缘生长顺序存到序列中.

4)将序列中的类圆弧边缘按照像素点的数目进行排序并将像素点过少的类圆弧移除.

5)通过最小二乘法拟合与三点定圆检测相结合的方式过滤掉一些不符合的类圆弧边缘.

6)对剩下的每一条类圆弧利用最小二乘法拟合求取半径和圆心并排除掉与三点定圆检测结果偏差过大的类圆弧.

7)将半径和圆心坐标的偏差在一定范围内的类圆弧聚成一类(认为是同一个圆上的圆弧)，再次进行最小二乘法拟合得到半径r以及圆心坐标.在序列中按一定比例选取一定数量的坐标点对得到的圆进行验证，过滤掉误差过大的圆.

8)如果步骤6)所得的圆中参与拟合的像素点的数目大于一个动态阈值(2πrj)，则认为是该圆是所求圆.

图5 圆检测算法流程图Fig.5 Flow chart of the new circle detection algorithm

3 实验结果及分析

实验环境采用硬件配置为Intel酷睿i5 480M，主频2.67 GHz，内存为6 GB；软件配置为Windows 8 64位操作系统，VS 2013软件开发平台.21HT是OpenCV中目前为止唯一一种圆检测算法，它是一种非常优秀的改进的霍夫变换，在现实中有广泛的应用.在本实验中使用OpenCV中的21HT与提出的圆检测算法进行比较.

3.1 实验1

为了验证新型圆检测算法的准确性、速度以及抗干扰性，实验中采用了大小为400像素X550像素的合成图片以及在原图中加入10 000个噪声的合成图片.原图如图6(a)中所示，噪声图片如图6(d)所示，其中共有7个圆，包括同心圆、残缺圆、相交圆.图6(b，c)分别为21HT算法和新型圆检测算法在原图中圆检测效果，图6(e，f)分别为21HT算法和新型圆检测算法在噪声图片中的圆检测效果，表3为2种算法在加入噪声前后的检测准确度和检测速度的对比实验结果，表4为2种算法的抗干扰性能对比结果.

图6 圆检测算法效果Fig.6 Experiment on the images

圆检测结果对比算法原图圆数量/个检测出圆数量/个正确检测数量/个检测正确率/%运行时间/ms未加入噪点21HT76685.7131.47新型算法77710010.23加入噪点后21HT76685.7140.51新型算法77710010.45

表4 圆检测误差Table 4 Error of circle detetion results 像素

3.2 实验2

为了验证该算法对实际图片的检测能力，使用拍摄的照片进行圆检测.实验采用778像素×656像素的拍摄照片以及加入10 000个噪声的照片.原照片如图6(a)中所示，加入噪声后的照片如图7(d)所示，其中一共有4个圆.图7(b，c)分别为21HT算法和新型圆检测算法在照片中的圆检测效果，图7(e，f)分别为21HT算法和新型圆检测算法在加入噪声后的圆检测效果，表5为2种算法在加入噪声前后的检测准确度和检测速度的对比实验结果.

3.3 实验分析

实验表明：新型圆检测算法对同心圆、残缺圆以及相交圆都具有良好的检测性能.新型圆检测算法不仅正确率高于21HT算法，而且检测速度较21HT有很大的提升.新型圆检测算法对加入噪声后的图片有较强的检测稳定性，具有较强的抗干扰能力.

图7 圆检测算法效果Fig.7 Experiment on the images

圆检测结果对比算法原图圆数量/个检测出圆数量/个正确检测数量/个检测正确率/%运行时间/ms未加入噪点21HT4225089.32新型算法44410022.68加入噪点后21HT4225083.63新型算法44410023.13

4 结 论

提出的检测圆的方法从圆弧的特性出发，只检测具有圆弧特性的边缘，因此提升了检测效率和准确性.通过打断分叉边缘链以及根据圆弧边缘特性的方法提取边缘链并完成边缘坐标的有序存放，在此基础上利用最小二乘法拟合与三点定圆相结合的方式筛选圆弧链.然后将半径和圆心坐标的偏差在一定范围内的圆弧聚成一类，对其最小二乘法拟合得到求圆.该方法检测速度快，稳定性高，抗干扰能力强，可以在一张图像中检测多个圆、残缺圆、同心圆以及相交圆.

[1] 张江鑫,沈小兰,王辉,等.快速随机Hough变换多直线检测算法[J].浙江工业大学学报,2013,41(3):346-350.

[2] 陈戈珩,李华杰,房晓伟,等.基于相位一致性和Hough圆的贴片机视觉定位系统的研究[J].科学技术与工程,2015,15(27):59-63.

[3] 吴全玉,周署,俞洋,等.Hough算法在印刷电路板焊孔缺陷检测中的应用[J].工业仪表与自动化装置,2015(6):56-59.

[4] 高宇鹏,李益明,胡众义,等.基于Hough变换倾斜文档校正的改进方法[J].浙江工业大学学报,2013,41(1):106-109.

[5] XU L, OJA E, KULTANEN P. A new curve detection method: randomized Hough transform (RHT) [J]. Pattern recognition letters,1990,11(5):331-338.

[6] XU L, OJA E. Randomized Hough Transform (RHT): basic mechanisms, algorithms, and computational complexities [J]. Computer vision & image understanding,1993,57(2):131-154.

[7] 舒龙庆,曾垂力.一种基于圆的几何特性改进的圆检测随机算法[J].集成技术,2015(2):46-49.

[8] 周冬跃,陈健明,林福民,等.一种基于粒子群优化算法的快速圆检测方法[J].光电子·激光,2016(9):949-956.

[9] 秦开怀,王海颍,郑辑涛.一种基于Hough变换的圆和矩形的快速检测方法[J].中国图象图形学报,2010(1):109-115.

[10] 石希,赵殿鹏,徐婕,等.基于最小二乘法的混凝土相关性曲线的研究[J].浙江工业大学学报,2014,42(4):388-392.

[11] 陈明晶,方源敏,陈杰,等.最小二乘法和迭代法圆曲线拟合[J].测绘科学,2016,41(1):194-197.

[12] 孙国栋,杨林杰,张杨,等.基于三点迭代的聚类圆拟合算法[J].制造业自动化,2015(13):76-78.